基于LSTM网络高速列车悬挂系统故障预测方法研究

张传凯，刘佳龙

（1.北京市地铁运营有限公司，北京 100005；2.北京地铁工程管理有限公司，北京 100005；3.东北大学机械工程与自动化学院，辽宁沈阳 110819）

1 研究背景

随着高速列车运营质量普遍性提升以及车辆运行速度不断提高，其安全性成为运行与发展首要问题。悬挂系统作为高速列车重要组成部分，对其开展故障预测研究至关重要。Ye等将多尺度排列熵(Multiscale Permutation Entropy，MPE)与线性局部切空间排列（Linear Local Tangent Space Alignment，LLTSA)结合，实现对悬挂系统故障诊断。其他方法如采用卡尔曼滤波器、模糊神经网络方法同样能够对高速列车悬挂系统进行故障诊断。但是，高速列车悬挂系统故障预测研究却未得到普遍开展，目前我国高速列车主要是采用里程计划维护策略，随着智能化和信息化不断推进，开展相关故障预测研究越来越重要。

由于长短时记忆（Long Short-Term Memory，LSTM）网络在故障诊断领域优于深度神经网络（Deep Neural Network，DNN）、循环神经网络（Recurrent Neural Network，RNN）、卷积神经网络（Convolutional Neural Network，CNN）的性能，因此广泛应用于故障预测诊断领域。例如，利用LSTM网络对旋转机械进行剩余寿命预测；通过LSTM网络对舰船软件运行进行健康状态预测；建立齿轮箱正常运行时的油温监测LSTM网络模型，实现对齿轮箱故障预测；将基于一对多法构造支持向量机长短时记忆网络（SVM-LSTM）的寿命预测方法应用于高铁牵引系统中。因此，LSTM网络故障预测已是各行业中普遍采用的方法。

高速列车运行时原始振动加速度信号呈现非线性、非平稳特征，在每个数据采集点表现出数据波动较大且噪声干扰较明显，无法直接从原始信号中判断早期故障发生时间。文章以时域均方根值和峰度值指标为例，构建其健康因子（Health Indicators，HI）曲线，并通过 LSTM网络对关键部件进行健康状态预测，以期证明基于LSTM网络的高速列车悬挂系统故障预测方法行之有效。

2 LSTM网络概述

LSTM网络是一种特殊的RNN，通过学习算法以及精准控制输入门、输出门及遗忘门的开启和关闭来解决普通RNN在长序列训练中梯度消失和梯度爆炸问题。

RNN结构及其展开图如图1所示，xt为t时刻输入；st为t时刻隐藏层特征；ot为t时刻的输出；U，V，W分别表示为输入层、输出层和隐藏层的权值参数。t时刻隐藏层计算公式如下：

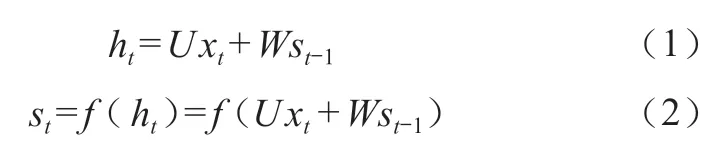
式（1）～式（2）中，f（•）为非线性激活函数；ht为t时刻隐藏层状态值；U和W为参数矩阵；st-1为t-1时刻隐藏层特征。

ot在t时刻输出计算公式如下：

式（3）中，g（•）为归一化指数函数（Softmax）；V为参数矩阵。

LSTM网络与RNN区别在于循环神经单元的节点设置。针对RNN不可长期记忆问题，LSTM网络增加一个长期记忆单元状态（cell -state），并引入输入门、输出门以及遗忘门3个门控循环单元，用于控制记忆更新与遗忘，保证重要信息始终被记忆，同时遗忘掉不太重要信息，实现记忆在隐含层单元中存储和流动，即允许网络学习何时忘记历史信息以及何时用新信息更新存储器单元。通过学习算法以及精准地控制输入门、输出门以及遗忘门的开启和关闭，解决普通RNN在长序列训练中的梯度消失和爆炸问题。

LSTM网络遗忘门控制单元计算公式如下：

式（4）中，ft为遗忘门控制单元，代表遗忘上一层隐藏细胞状态的概率；遗忘门的输入分别为上一序列隐藏状态ht-1和当前时刻序列数据xt；σ（•）为激活函数，通常使用S型函数（sigmoid）；LSTM网络通过上一时刻输出ht-1和当前时刻输入xt共同组成输入向量[ht-1，xt]；bf为遗忘门偏置向量；Wf为遗忘门权值矩阵，则得到[0，1]范围内的遗忘门输出数值ft。

图1 RNN结构及其展开图

LSTM网络单元中输入门是更新“新输入信息”到当前时刻的单元状态，由2部分组成，计算公式如下：

式（5）～式（6）中，it为输入门控制单元，生成的向量确定某些信息在短期内状态ht-1用于更新细胞状态；是经it测试后被添加到长期细胞状态内产生；bi和bc为输入门偏置向量；Wi和Wc为输入门权值矩阵。激活函数tanh为双曲正切函数。

LSTM网络最新更新长期状态计算公式如下：

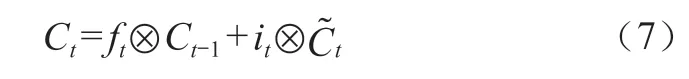
式（7）中，基于之前时刻状态Ct-1与遗忘门输出ft的乘积决定将过去长期记忆单元中不相关信息进行遗忘，加上输入门的结果，从当前时刻输入中提取紧要信息，对短期记忆单元中信息进行更新，以此决定最新的更新长期状态，其中为元素相乘。

LSTM网络输出门控制单元计算公式如下：

式（8）～式（9）中，ot为输出门状态；bo为输出门偏置向量；Wo为输出门权值矩值；ht为t时刻输出门控制单元输出。

3 基于 LSTM网络高速列车转向架健康状态预测

3.1 高速列车转向架健康状态退化模型

在进行多体动力学建模过程中，需要考虑所建模型与实际车型的高度相似性，使用多体动力学分析软件SIMPACK建立高速列车转向架及整车非线性动力学模型时，需要将实际列车运行过程中的轮轨接触非线性几何关系和作用力考虑其中。在软件中建立高速列车转向架动力学模型，如图2所示。

3.2 转向架健康状态预测步骤及评价指标选取

为保证高速列车正常运行，需要在构架、车身和轴箱等重要位置添加传感器采集实时信息，并通过信息融合反映高速列车典型部件实时健康状态，设置关于高速列车横向减振器健康程度，从100%、90%、…、10%进行模拟仿真，高速列车转向架退化状态建模流程主要包括以下5个部分，具体步骤如下。

图2 高速列车转向架动力学仿真模型

（1）退化振动数据采集。选取传感器采集的高速列车转向架横向减振器运行过程不同程度的历史退化数据，采样频率为243 Hz，列车运行仿真时间为3 990 s，选取固定通道传感器采集原始故障信息数据，每个通道采集959 670个数据点。以其中某一通道车体中部横向振动加速度传感器为例，其原始振动加速度信号如图3所示，全寿命周期过程中，随着横向减振器不同程度损坏以及外界其他因素影响，原始振动加速度信号在每个数据采集点表现出数据波动较大且噪声干扰较明显，无法直接从原始信号中判断早期故障发生时间。

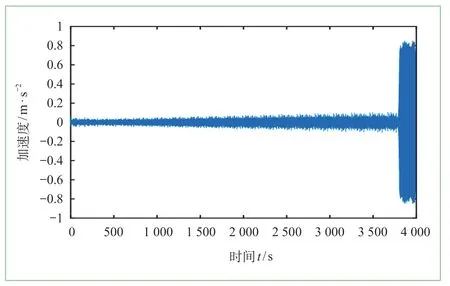
图3 车身中部横向加速度原始信号

（2）数据归一化。将原始振动加速度信号归一化至[0，1]区间内，归一化数据计算公式如下：

式（10）中，x*为归一化数据；x为原始数据；xmin和xmax分别为每个传感器在退化时间序列的最大值和最小值。

（3）HI健康因子构建。基于上述多通道传感器进行特征融合，构建能够表征高速列车横向减振器性能状态程度变化的健康因子曲线。

（4）健康状态预测。基于上述获得的HI健康因子曲线通过实时LSTM网络预测模型对高速列车健康状态进行实时预测。

（5）健康预测算法评估。对LSTM网络预测算法进行性能评价，评价指标采用均方根误差RMSE和平均绝对误差MAE。

文章采用RMSE和MAE两个评价指标对提出的预测算法进行性能评价。计算公式如下：

式（11）～式（12）中，n为测量次数；ηi为1组测量值与平均值的偏差，i=1，2，…，n。

3.3 基于 LSTM网络高速列车转向架健康状态预测

实验中分别基于多维振动加速度信号数据构建表征高速列车健康状态的均方根值和峰度值2个健康因子的HI健康状态曲线，共444个样本，以其中356个前期样本作为训练样本，以89个后期样本作为测试样本进行预测，根据其他研究对象文献作为参考，具体实验参数如表1所示。

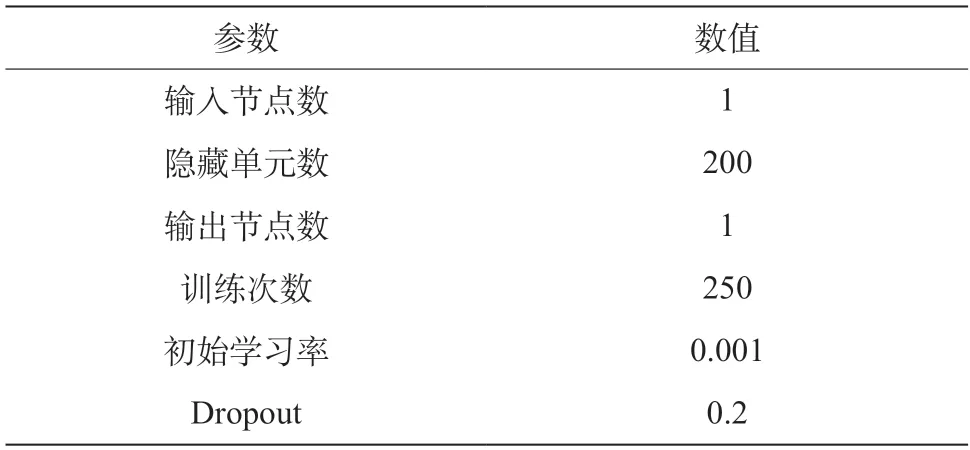
表1 高速列车转向架健康状态预测实验参数

根据以上实验参数设置，分别从均方根值、峰度值2个角度对高速列车的实时健康状态进行预测，均方根值健康因子曲线如图4所示，从图中可知，均方根值在高速列车健康状态退化过程中有所增加，将预测值与观测值数据进行对比，如图5、图6所示。

从图5可知预测值与实际观测值无论是从趋势还是从数值上都比较吻合，只是在第80个样本之后预测有一定偏差。从图6所示的误差图可以看出，样本之间的误差值有所增加，误差绝对值范围为[0.000 6，0.081 3]，所得RMSE为0.016 3，MAE为0.012 7。

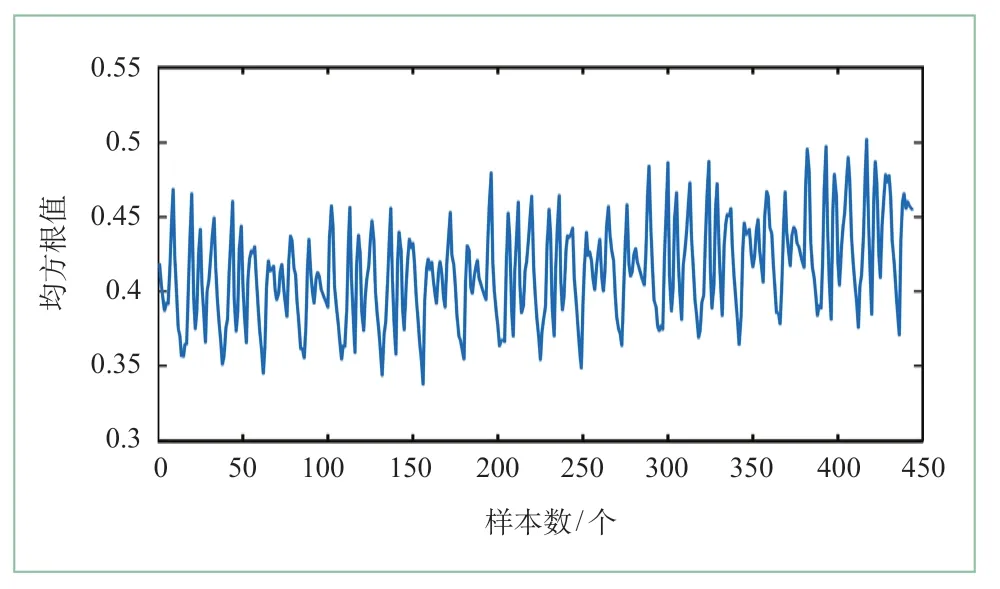
图4 均方根值健康因子曲线

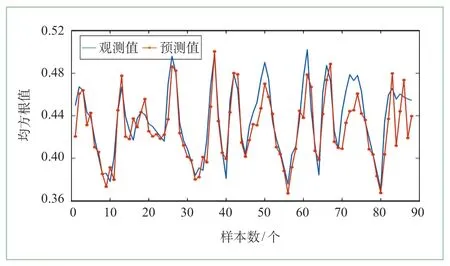
图5 均方根值健康因子观测值与预测值对比曲线

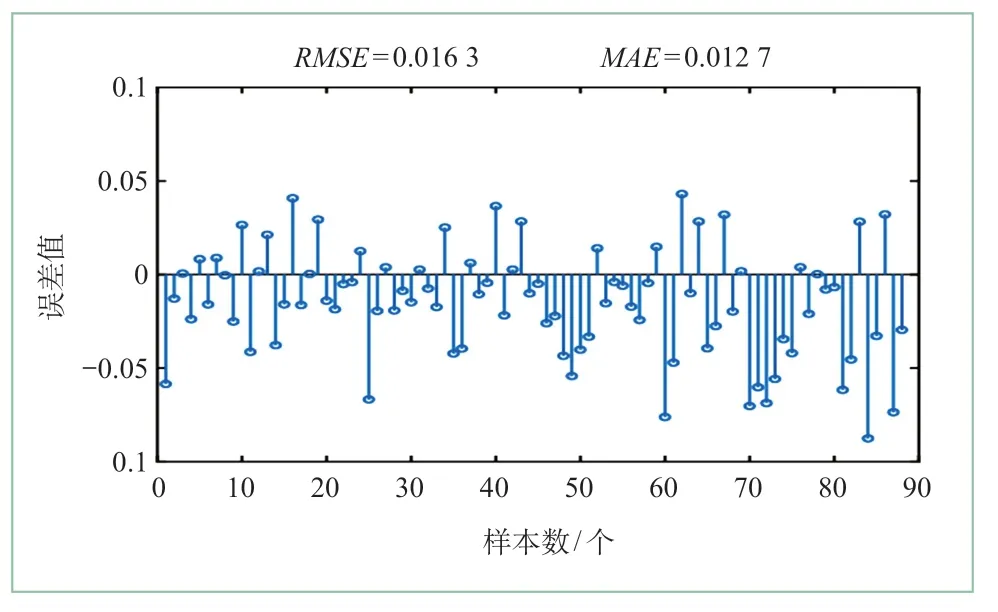
图6 均方根值健康因子预测误差值

根据实验参数设置，从峰度值角度对高速列车实时健康状态进行预测，高速列车运行退化状态峰度值健康因子曲线如图7所示。

从图7中可知，峰度值在高速列车健康状态退化过程中有所增加，将预测值与观测值进行对比如图8、图 9所示。

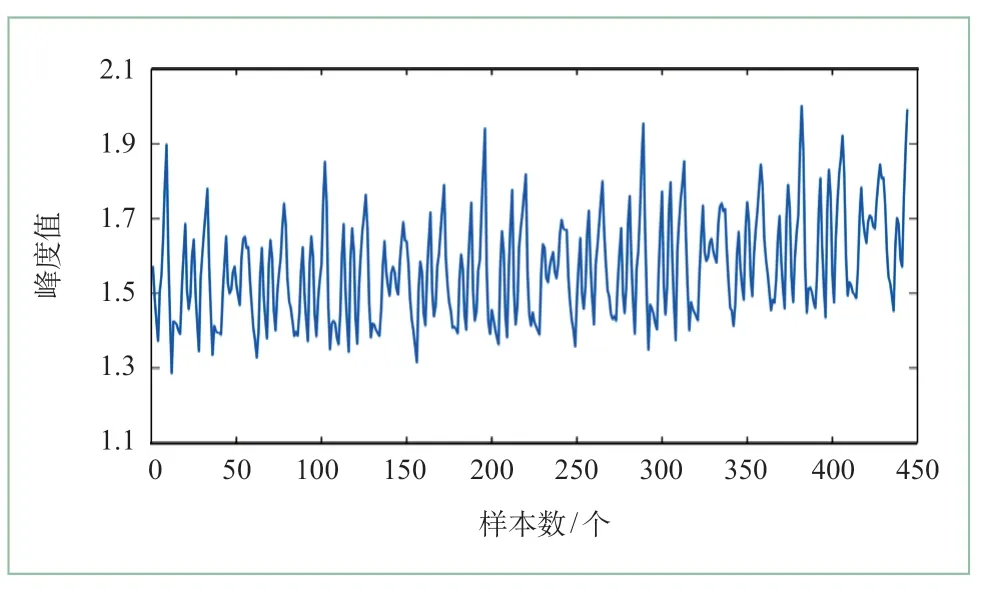
图7 峰度值健康因子曲线

图8 峰度值健康因子观测值与预测值对比曲线

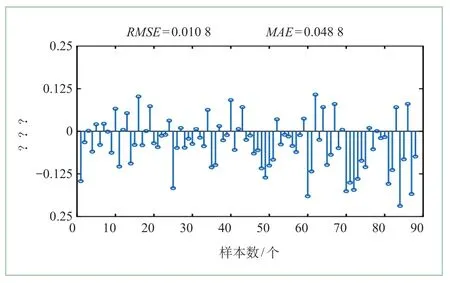
图9 峰度值健康因子预测误差值

从图8可知预测值与实际观测值无论是从趋势还是从数值上都比较吻合，图9的误差图中可以得知样本之间的误差值无较大明显变化，误差绝对值范围为[0.000 3，0.238 6]，所得RMSE为0.010 8，MAE为0.048 8。

综上所述，利用LSTM网络复杂数据趋势学习能力，在高速列车悬挂系统故障预测中取得了良好效果。

以均方根值为健康因子预测，其RMSE和MAE分别为0.016 3和0.012 7；以峰度值为健康因子预测，其RMSE和MAE分别为0.010 8和0.048 8。经分析，以上2种健康因子误差值均较小，同时结合图5、图8，可以得出预测数据和实际观测数据拟合度很高，预测数据的趋势符合实际观测数据的趋势。

因此，文章所采取的基于LSTM网络高速列车悬挂系统故障预测方法所得到的预测值可以反映出实际未发生的装备退化过程，从而实施针对性的健康管理工作，是一种可行的预测高速列车悬挂系统故障方法。

4 结论

文章提出了一种基于LSTM网络的高速列车转悬挂系统故障预测方法。利用SIMPACK获得悬挂系统在各健康状态下运行的仿真实验数据，提取其均方根值和峰度值特征构建HI曲线，通过LSTM网络对其进行分析与预测，得到了与实际观测值误差很小的预测值，预测值HI曲线与实际观测值HI曲线拟合程度很高。实验结果验证了文章所提出的高速列车悬挂系统故障预测方法可行性。