车轮不圆顺轮轨滚动接触行为的动态有限元仿真方法
(西南交通大学牵引动力国家重点实验室,四川成都 610031)
1 研究背景
作为铁路车辆中最为核心的走行部件——车轮,其系统的失效将会造成灾难性后果及巨大的经济损失。随着列车速度的不断提升和轴重的增加,车轮不圆顺伤损问题日益严重,严重影响轨道-车辆零部件的服役寿命和车辆的乘坐舒适性,甚至威胁行车安全,已成为轨道交通领域备受关注和亟待解决的难点问题之一[1-3]。
目前,针对车轮不圆顺条件下的轮轨关系研究通常采用多体动力学方法和有限元方法[4-6]。多体动力学方法大多基于Hertz接触理论和稳态滚动假设,不能很好地描述轮轨系统的几何、材料和接触非线性,无法考虑轮轨相互作用的动态效应,且不能直接求解轮轨系统的应力/应变状态。有研究表明,当研究对象无明显结构变形(即频率低于第一振型)时,多体动力学方法才是准确和有效的;而在频率高于第一振型(大于84 Hz)时,其求解精度会显著降低[7-8]。基于连续介质力学的有限元方法不仅可以考虑到局部变形,还可以考虑到强非线性、应变率效应和应力波传播效应,被认为能够更好地求解轮轨动态力学响应,近年来在求解轮轨滚动接触行为研究中得到了越来越多的应用[9-12]。
然而,在采用有限元方法求解车轮不圆顺引起的轮轨动态响应问题时,通常存在以下2个问题:①车轮踏面缺陷具有随机性(包括尺寸、形状、位置及分布的随机性),造成几何模型复杂,有限元建模难度很大;②车轮踏面缺陷处的网格精细划分会引起有限元模型单元数量较大,造成计算时间过长,并且缺陷处不规则网格的畸变极易导致计算不稳定。针对上述问题,本文将车轮不圆顺转换为轮轨接触位移不平顺,引入伪随机数,生成满足多种随机分布特性的轮轨接触位移不平顺激励,并将其施加到不含缺陷的三维轮轨滚动接触有限元模型中,极大地简化了不圆顺车轮-钢轨间的动态接触行为仿真研究。
2 车轮不圆顺轮轨接触数学模型
车轮不圆顺(如车轮扁疤、踏面剥离、车轮多边形等)是引起轮轨接触不平顺的主要原因之一。本文建立不圆顺车轮和钢轨滚动接触数学模型,基于轮轨滚动接触几何关系,通过推导由车轮踏面缺陷引起的轮轨接触不平顺数学表达式,实现车轮不圆顺向轮轨接触位移不平顺的转换。
2.1 车轮扁疤
含扁疤车轮-钢轨间滚动接触情况如图1所示。在低速运行情形下(图1a),车轮围绕扁疤前角转动至扁疤与钢轨平行后,紧接着围绕扁疤后角开始转动,直到越过整个车轮扁疤区域;在高速运行情形下(图1b),车轮与钢轨在扁疤区域内将会出现短暂的接触损失(车轮脱离钢轨),并在重力作用下以某一水平初速度做平抛运动,随后扁疤后角撞击钢轨或直接越过扁疤继续滚动。
本文采用具有最小曲率半径的车轮轮廓运动轨迹描述实际的轮轨接触位移不平顺[13]。对于新扁疤,低速运行情形下的轮轨接触位移不平顺Zf(ξ)方程可表示为[13]:

而在高速运行情形下,结合平抛运动以及新扁疤车轮轮廓运动轨迹,其轮轨接触位移不平顺Zf(ξ)为:
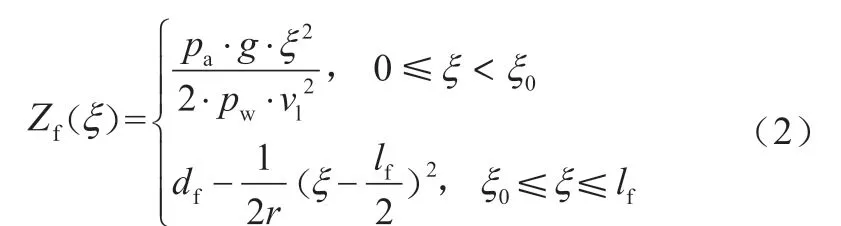
式(1)~式(2)中,df,lf分别为新扁疤的深度和长度,其中df=lf2/ 8r;pw为车轮自重;pa为轴重;vl为水平初速度;g为重力加速度;ξ0为平抛运动结束后车轮与钢轨接触时新扁疤位置到扁疤起点的水平距离。
对于旧扁疤,低速运行情形下的轮轨接触位移不平顺Zr(ξ)可表示为[13]:

而高速运行情形下的Zr(ξ)则可表示为:
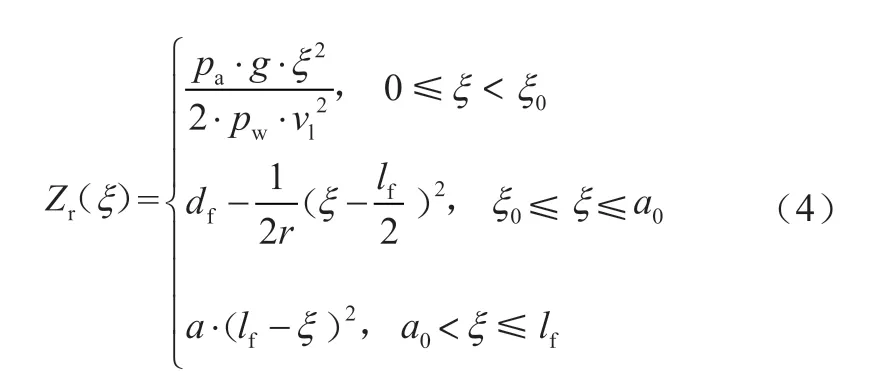
式(3)~式(4)中,ξ1,ξ3分别为旧扁疤前、后2个端点与中心区域的交点;a0为旧扁疤后端与中心区域的交点;a为确定过渡范围的常量;df,lf分别为旧扁疤的深度和长度,其中df=alf2/4(2ar+1)。
2.2 踏面剥离
对于含踏面剥离的车轮,由于钢轨顶面曲率的存在使得车轮剥离区域与钢轨的接触状态变得较为复杂,因此分析中常将其简化为规则的半椭球形。由于含踏面剥离车轮-钢轨间动态接触过程与扁疤类似,故可采用类似的分析方法推导规则踏面剥离造成的轮轨接触位移不平顺。踏面剥离的轮廓线可以简化成一个圆柱体(车轮)与半椭球体(剥离)的交线,如图2所示。此空间曲线可表示为:
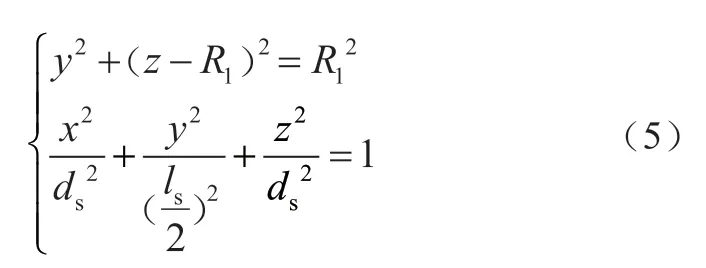
式(5)中,(x,y,z)为车轮和踏面剥离在空间坐标系中的位置;ds,ls分别为踏面剥离的深度和长度。

图1 含扁疤车轮-钢轨间滚动接触情况

图2 含踏面剥离车轮与钢轨接触示意图
通过几何关系推导,可得到低速运行情形下踏面剥离引起的轮轨接触不平顺Z(y)表达式为:

而高速运行情形下的Z(y)表达式为:

式(6)~式(7)中,R1,R2分别为车轮名义滚动圆半径和轨面曲率半径;ws为踏面剥离宽度;m为轮对自重的一半;v为列车恒定速度;FS为作用在轮对上等效车体载荷的一半;θ为轨底坡角度;p为平抛运动阶段的水平距离。
2.3 车轮多边形
基于不圆顺车轮半径沿圆周方向的变化情况分为周期性和非周期性2种类型,其中非周期性多边形车轮的径向偏差可以看成不同谐波的叠加。周期性不圆顺(三阶)车轮-钢轨间的滚动接触过程如图3所示。
对于周期性多边形车轮,其径向偏差∆r可表示为[14]:

式(8)中,θ为车轮转过的角度;A,N分别为某阶车轮多边形所对应的幅值和阶数。
其中车轮多边形波长λp和阶数N之间的关系可表示为:

非周期性车轮多边形磨耗可认为是一系列谐波的叠加,其中每个谐波具体指任意阶的多边形磨耗。因此,非周期性多边形车轮引起的轮轨接触位移不平顺Z(θ)可表示为[15]:
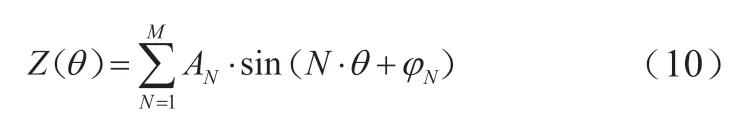
式(10)中,φN为相位角,且在0~2π 之间服从多种随机分布;AN为某阶多边形对应的幅值;M为车轮不圆顺总的阶次。
3 车轮踏面缺陷随机性表征
如上所述,车轮踏面缺陷在尺寸、形状、位置及分布上具有随机性,本文通过选取合适的分布函数实现车轮踏面缺陷的随机化描述,进而得到由车轮踏面缺陷引起的轮轨接触随机不平顺位移激励。
3.1 随机分布函数
随机数按生成方式整体上可分为真、伪随机数2类[16]。其中真随机数在生成之前无法预测,一般基于物理方法,通过一系列复杂过程产生;伪随机数大多根据给定算法由数学方法产生,从原理上是可以预测的,通过选择合理的计算方法及参数,产生具有良好特性的随机数。此外,伪随机数还具有生成效率高、实现简单等特性。因此,本文采用伪随机数表征车轮踏面缺陷的尺寸、形状、位置及分布随机特性。
伪随机数的产生算法有很多,本文从计算速度、生成周期、独立性和均匀性等方面综合考虑,选取性能较好的线性同余法[17]。线性同余法是借助同余运算生成区间[0,1]内服从均匀分布的伪随机数,其具体计算公式如下[18]:
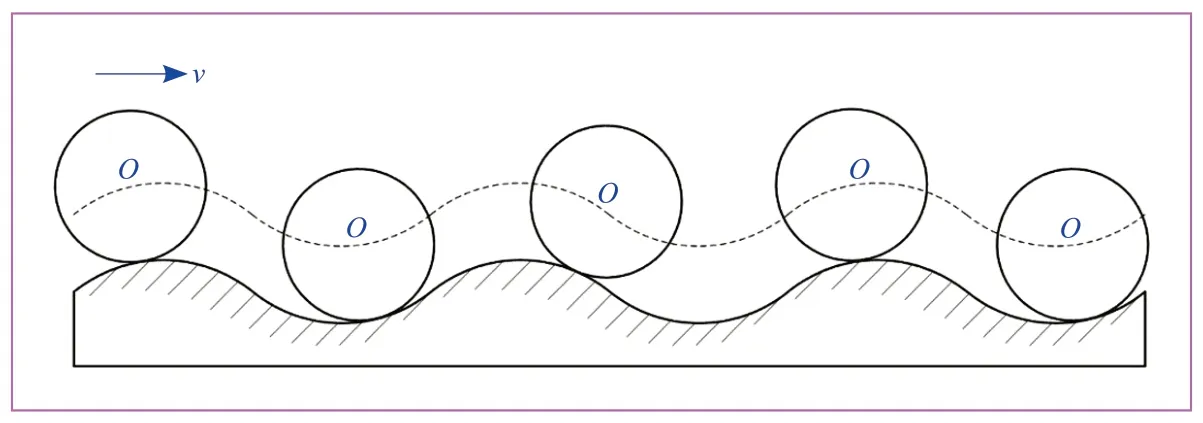
图3 周期性不圆顺(三阶)车轮-钢轨间的滚动接触过程

式(11)中,{rn}为[0,1]上的随机序列;xn,xn-1分别为此随机序列中的第n和第n-1个随机数;b,c和M分别为乘子、增量和模,均是系统给定的常量;初值x0为种子。
由于车轮踏面缺陷在形成过程中的复杂性和不确定性造成其在车轮圆周上的分布情况极具随机性,因此轮轨接触位移不平顺激励通常可用多种随机分布函数描述。例如:①在理想情况下,车轮踏面圆周上出现缺陷的位置是随机的,且在任意一个位置出现的概率相等,故可用均匀分布的随机数描述;②当车轮踏面缺陷的随机性有多个独立随机因素叠加时,可认为每个随机变量都满足正态分布;③当车轮在某个位置已经出现缺陷,此后车轮每滚动到此处都会产生较大的振动冲击,并在一定范围内冲击力会随着车轮的滚动而不断衰减,在此处再次产生缺陷的概率最大,往后依次递减,此时可认为近似符合指数分布。因此,可以通过对标准均匀分布、正态分布、指数分布等进行相应变换使其满足特定区间内的随机分布类型,实现车轮踏面缺陷的随机化描述。
3.2 轮轨接触随机不平顺位移激励
基于踏面缺陷引起的车轮不圆顺与轮轨接触位移不平顺之间的转换关系,本文采用线性同余法生成满足各种随机分布函数的轮轨位移不平顺激励。限于篇幅,这里仅以踏面剥离为例,给出不同随机度λz下单个踏面剥离形貌及相应的轮轨接触位移不平顺曲线,如图4所示。
4 有限元仿真方法及验证
4.1 有限元模型
借助Hypermesh软件建立包含轨下基础结构的三维轮轨滚动接触有限元仿真模型,如图5所示。车轮为S1002CN型踏面,半径为430 mm;钢轨为CN60型,轨底坡为1 :40。整个模型由弹簧-阻尼离散单元(扣件)和8节点实体单元2部分组成。为减小计算量,将弹簧阻尼单元连接区域和轮轨接触区域的网格进行细化(4 mm×4 mm),其余网格进行适当过渡。整个模型包含1 177 793个节点和1 001 343个单元(包括实体单元和离散单元)。

图4 不同随机度λz 下单个踏面剥离的形貌与轮轨接触位移不平顺激励

图5 三维轮轨滚动接触有限元仿真模型
车轮和钢轨均采用*MAT_PLASTIC_KINEMATIC材料模型描述,该模型可以模拟材料的随动强化特性,且可通过Cowper-Symonds本构关系考虑轮轨材料的应变率效应。车轴采用*MAT_ RIGID材料模型描述,轨下基础结构各部分采用*MAT_ELASTIC材料模型描述,弹簧和阻尼系统采用*MAT_SPRING_ELASTIC和*MAT_DAMPER_VISCOUS材料模型描述。仿真中轮轨系统各部件的力学性能参数如表1所示。
为实现轮对运动过程中的稳定与平衡,仿真中对路基底部和车轴端部所有节点分别实施全约束和轴向平动约束,给轮对设置相应的初始平动和转动速度实现其在钢轨上的滚动。根据欧洲标准,在车轴两端分别施加P1=77.56 kN和P2=110.41 kN 2个集中力等效轴重载荷(17 t)。车轮与钢轨、车轴之间均定义基于罚函数法的Automatic_Surface_To_Surface,轨下基础结构各部件之间定义Tied_Surface_To_Surface接触。如上所述,为避免车轮踏面缺陷带来的有限元直接建模诸多问题,仿真中将车轮踏面缺陷引起的轮轨接触位移不平顺激励作为初始边界条件,通过将关键字*PRESCRIBED_MOTION_SET输入到钢轨顶面的相应节点上,并采用强迫节点运动方式实现对车轮踏面缺陷的模拟。

表1 仿真中轮轨系统各部件的力学性能参数
有限元仿真中的积分算法通常包括隐式和显式2种。显式算法适用于求解波的传播、非线性动力学等高频、瞬态问题,其积分时间步一般很小,且求解速度很高,不存在收敛性问题。其瞬态动力学分析方程为:

式(12)中,[M],[C],[K]分别为结构质量、阻尼和刚度矩阵;{F(t)}为结构外载荷;为结构节点加速度矢量;为结构节点速度矢量;为结构节点位移矢量。
由于高速轮轨滚动接触涉及高频、瞬态动力学分析,且必须考虑动态效应的影响,故本文选用显式积分算法。
4.2 方法应用及验证
基于上述动态有限元仿真方法(为与基于不圆顺车轮真实几何轮廓的直接建模方法区别,下面称为位移激励法),以车轮扁疤为例,采用LS-DYNA软件求解不圆顺车轮-钢轨间动态响应与接触行为,并与直接建模得到的仿真结果相比较,以验证该方法的计算准确性和精度。
在特定工况(v=200 km/h,l=40 mm)下,基于位移激励法和直接建模法计算的轮轨垂向接触力-时间曲线及差异性[19]如图6所示。可以看出,除峰值力稍有差异外,这2种方法的计算结果吻合较好;不同速度和扁疤长度下2种方法得到的峰值力相对误差均不超过17.8%。如前所述,高速轮轨关系研究中还必须考虑轮轨动态效应,特别是轮轨系统材料的应变率效应。图7所示为含车轮扁疤条件下,材料应变率效应对轮轨系统应力状态及分布规律的影响。可以发现,在不考虑应变率效应时的轮轨接触应力峰值分别为583.3 MPa和549.4 MPa,而在考虑应变率效应时的轮轨接触应力峰值为648.4 MPa和626.8 MPa,相应增加了65.1 MPa和77.4 MPa。这表明应变率效应能够显著提高轮轨接触von Mises应力,但是对其分布情况几乎没有影响。

图6 车轮扁疤引起的轮轨垂向接触力响应

图7 车轮扁疤引起的轮轨接触von Mises应力状态及分布规律
上述含车轮扁疤的轮轨动态接触行为仿真示例表明,本文提出的将车轮不圆顺转换为轮轨接触位移不平顺的动态有限元仿真方法是可行、有效的。在考虑轮轨系统强非线性特征和动态效应影响的同时,能够较好地表征缺陷的随机性特点,并且有效地求解轮轨接触应力/应变状态,以及分析高速不圆顺车轮-钢轨间的滚动接触行为。
5 结语
针对采用有限元方法求解含踏面缺陷车轮-钢轨间滚动接触行为时的诸多困难,本文通过建立车轮不圆顺条件下的轮轨接触数学模型,提出了用轮轨接触位移不平顺代替车轮踏面缺陷的等效方法;基于线性同余法生成的伪随机数,通过选取合适随机函数实现了车轮踏面缺陷在分布位置、几何形状/尺寸和数量等方面的随机化表征,以初始位移激励形式施加到轮轨滚动接触仿真模型中,在考虑轮轨强非线性特征和动态效应影响的同时,有效地求解轮轨动态力学行为(应力/应变状态等);最后,通过与直接建模得到的仿真结果相比较,得出位移激励法与直接建模法的轮轨间动态响应吻合较好,验证了基于位移激励的车轮踏面缺陷有限元模拟方法是可行、有效的。该仿真方法为高速轮轨滚动接触关系的研究提供了一种新的思路。

