并联换向阀周向稳态液动力分析

熊城炜，陈德馨，刘 毅，，邹铭轩，王 涛

（1．安徽理工大学 机械工程学院，安徽 淮南 232001；2．浙大宁波理工学院，浙江 宁波 315100；3．浙江大学宁波研究院，浙江 宁波 315100）

液动力是液压阀工作过程中油液对阀芯产生的附加作用力［1］，是影响液压阀的重要因素［2］。负载口独立控制技术是一种利用双阀芯或多阀芯来实现液压执行元件进回油口独立调节的换向技术［3－4］，准确计算并有效地降低稳态液动力是负载口独立控制换向阀研究的关键。

Borghi等［5］通过改变阀芯阀套结构，对液动力进行了有效补偿；Jan Lugowski等［6］改进了原有的液动力理论。在国内，张海平［7］从动力学角度分析了液压滑阀稳态液动力的基本概念和计算方法；Tan等［8］分析了阀的各个参数对液动力的影响规律；Wang等［9］提出了阀芯旋转式换向阀的稳态液动力矩计算公式并对其进行了验证。

近年来，负载口独立技术在智能化工程机械［10－12］、装备机械［13］等领域中的应用越来越广泛。但是，在负载口独立技术实现换向的过程中，稳态液动力会对系统的工作稳定性产生影响。因此，如何计算稳态液动力，以及如何降低系统的稳态液动力，是负载口独立控制技术需要解决的问题。

针对负载口独立控制技术对稳态液动力和系统稳定性的要求，本文中提出了一种基于双阀芯并联结构的换向阀，建立了对应的数学模型和液动力模型，并进行了求解分析，得到了几种不同工况下系统的总液动力矩，验证了所述降低液动力矩理论的可行性，为新型负载口独立控制换向阀的结构设计提供了重要的理论依据，具有一定的指导意义。

1 工作原理

图1表示负载口独立控制并联换向阀系统原理，主要包括双作用液压缸、齿轮传动系统、2个并联阀机构、直线电机以及伺服电机。2个并联阀机构阀芯的轴向位移由各自对应的直线电机控制，V1并联阀与伺服电机同轴，V2并联阀通过传动机构（齿轮箱）与伺服电机相连；图1中ⅱ）、ⅲ）所示是由转阀阀芯台肩上均匀分布沟槽和阀套上相应分布窗口构成的阀口Ⅰ、Ⅱ、Ⅲ、Ⅳ。阀口Ⅰ、Ⅳ为一组，阀口Ⅱ、Ⅲ为另一组，相同组的阀口同时打开或闭合，不同组的则相反。

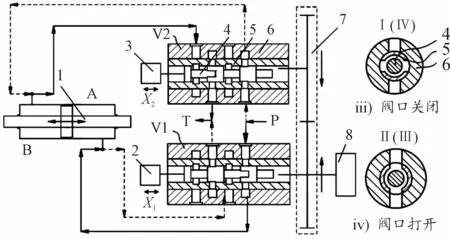
图1 并联式负载口独立控制换向阀原理示意图

如图1中ⅰ）虚线油路所示：油源P中的油液可进入V2并联阀的e腔室，当2个并联阀阀芯从零位（即Ⅰ、Ⅱ、Ⅲ、Ⅳ阀口均闭合时阀芯的位置）在直线电机和伺服电机的作用下运动到如图所示的位置时，阀口Ⅱ、Ⅲ打开，e腔室中的油液则通过阀口Ⅲ进入f腔室，并进入液压缸的左腔室B，从而推动液压缸活塞杆向右运动，将液压缸右腔室A中的油液压回V1并联阀的d腔室，再通过打开的阀口Ⅱ流入c腔室，最终使油液回到油箱T并完成整个液压缸活塞杆向右移动的过程。若2个并联阀阀芯从零位在直线电机和伺服电机的作用下反方向旋转相同的角度，则由油源P流入a腔室的油液通过打开的阀口I经过h腔室流入液压缸的右腔室A，从而推动液压缸活塞杆向左运动，将液压缸左腔室B中的油液压回V2并联阀的h腔室，在通过打开的阀口ⅳ流经g腔室回到油箱T，完成液压缸活塞杆向左运动的过程。

2 理论模型

分析时假定，系统供油压力Ps恒定，系统回油压力P0为0，且以图1所示伺服电机旋转方向为正向，并规定为液动力矩正向。图2为动力元件简化模型，当液压缸活塞杆向左移动时，阀口Ⅰ、Ⅳ打开；当液压缸活塞杆向右移动时，阀口Ⅱ、Ⅲ打开。

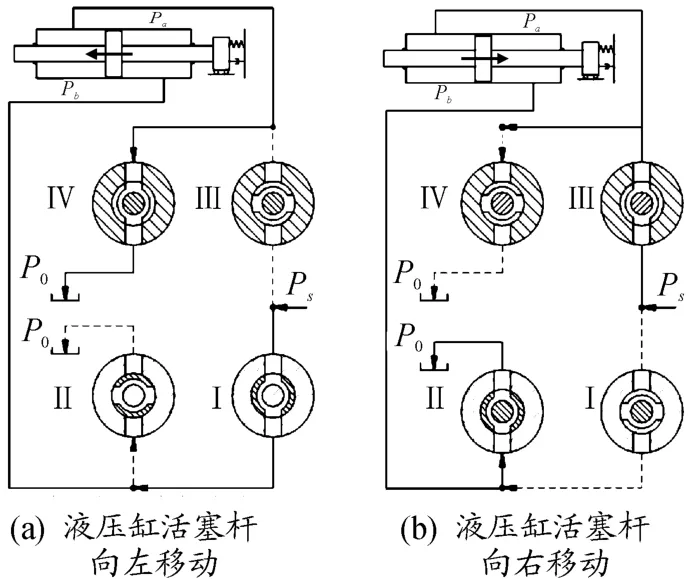
图2 简化模型示意图

2．1 阀口通流面积模型

图3 所示为并联阀工作过程中阀芯、阀套配合关系。由图3可知：阀口的通流面积主要与X1，2和y变量有关。其中，X1，2分别为一、二号阀芯阀轴向位移；y为阀芯旋转位移θ所对应的弦长。图中黑色部分即为阀口通流面积A。分析时，将阀口均关闭时的位置定义为阀芯旋转角位移和线性位移的零位（如图3所示的位置），即X1，2＝0，θ＝0。

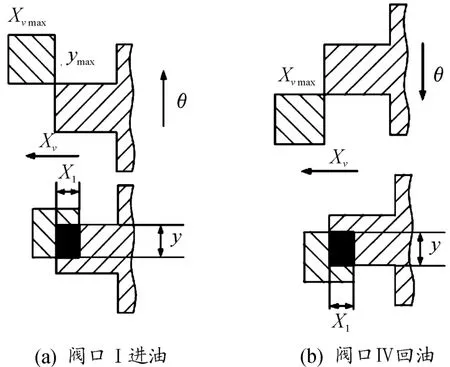
图3 并联阀阀芯阀套配合关系示意图

图中黑色区域即为阀口通流面积Ai，分析阀芯阀套配合关系可知，伺服电机正转时，阀芯旋转位移θ与开口重合部分弦长y之间应满足如下关系式：

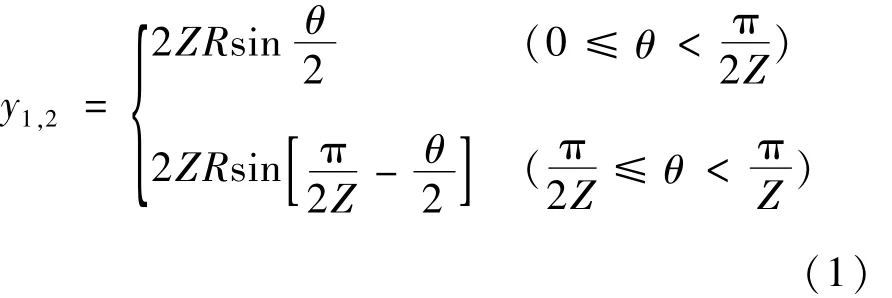
式中：y1、y2分别为一、二号并联阀对应的弦长；Z为阀芯台肩均布沟槽个数。

同理，伺服电机反转时，角位移θ与开口重合部分弦长y之间也满足上述关系式。由于在伺服电机正反转情况下，其周向液动力相同，因此为了简化，只分析伺服电机正转，即一号阀芯Ⅰ口进油、二号阀芯Ⅳ口回油时系统的总液动力。在伺服电机正转情况下，阀口通流面积的方程为

伺服电机正转：

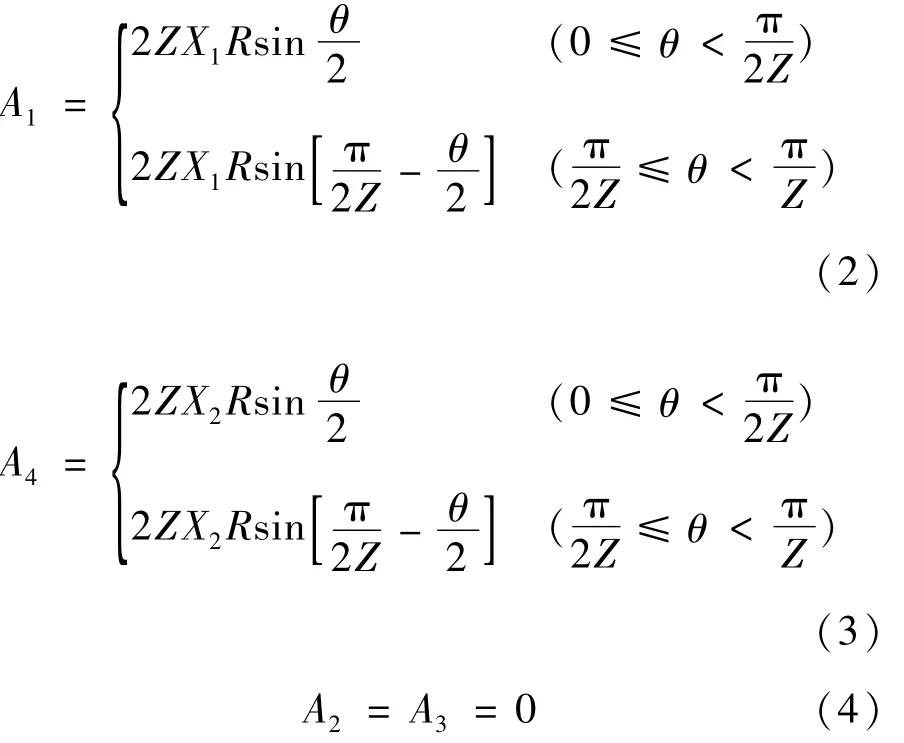
式中：X1、X2分别为一、二号并联阀阀芯轴向位移；A1、A2、A3、A4分别为阀口Ⅰ、Ⅱ、Ⅲ、Ⅳ的通流面积。

2．2 液动力模型

根据原理图提出的并联式负载口独立控制换向阀的结构，可知其工作过程中油液流动方向如图2所示，其中，（a）为进油时液压油流动方向，（b）为回油时油液流动方向，实线箭头方向即为油液流向。分析该图可知，在阀芯旋转过程中，当有油液流经阀口时，其产生的周向液动力如图4、图5所示。

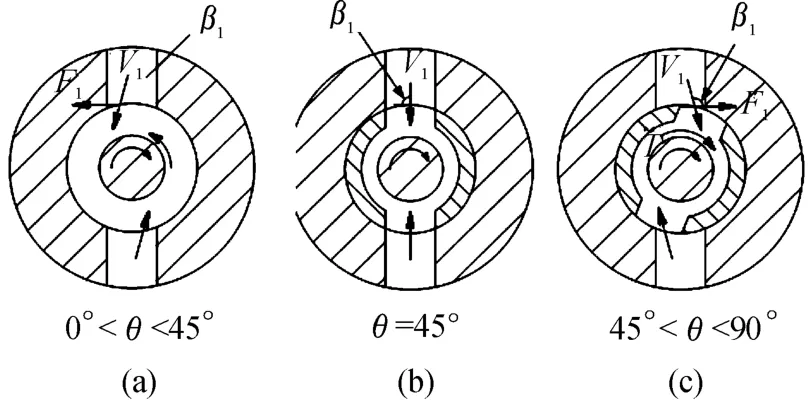
图4 进油口周向稳态液动力的产生示意图

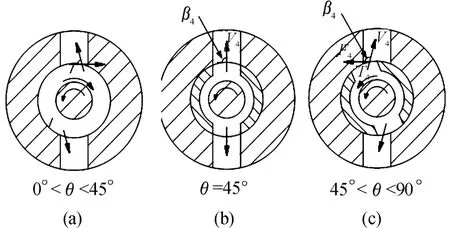
图5 回油口周向稳态液动力的产生示意图

由动量定理及液压转阀液动力理论［9］可知：一号阀芯Ⅰ口进油时，油液产生的周向液动力为

式中：β1为一号阀芯Ⅰ口进油时油液射流角在圆周方向上的夹角；q1、v1分别为油液在Ⅰ口处的流量和流速。因此，周向液动力矩可以表示为

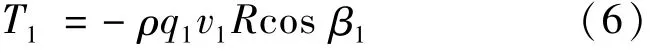
同理可知，二号阀芯Ⅳ口回油时，油液所产生的周向液动力为

式中：β4为二号阀芯Ⅳ口回油时油液射流角在圆周方向上的夹角；q4、v4分别为油液在Ⅳ口处的流量和流速。因此，二号阀芯回油时油液所产生的周向液动力矩可以表示为

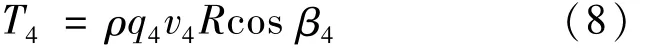
从图4中可以看出：在阀芯进油口旋转经过一个阀套开口的过程中，两者之间存在3个相对位置关系。其中，当阀芯旋转角位移小于45°时，两者重合部分面积逐渐增大（如图4（a）所示），其稳态液动力矩为逆时针方向，对阀芯旋转起阻碍作用；当阀芯旋转角位移等于45°时，两者重合部分面积最大（如图4（b）所示），其稳态液动力矩为0；当阀芯旋转角位移大于45°时，两者重合部分面积逐渐减小（如图4（c）所示），其稳态液动力矩为顺时针方向，对阀芯旋转起促进作用。

同理，从图5中可以看出：在阀芯回油口旋转经过一个阀套开口的过程中，两者之间也存在3个相对位置关系。其中，当阀芯旋转角位移小于45°时，两者重合部分面积逐渐增大（如图5（a）所示），其稳态液动力矩为顺时针方向，对阀芯旋转起阻碍作用；当阀芯旋转角位移等于45°时，两者重合部分面积最大（如图5（b）所示），其稳态液动力矩为0；当阀芯旋转角位移大于45°时，两者重合部分面积逐渐减小（如图5（c）所示），其稳态液动力矩为逆时针方向，对阀芯旋转起促进作用。

由并联式负载口独立控制换向阀阀芯之间的配合关系可知，当伺服电机正转时，一号阀芯旋转方向与伺服电机相同，二号阀芯旋转方向与伺服电机相反，则油液流经两阀芯阀口的液动力矩相反。因此，伺服电机正转时，总稳态液动力矩为

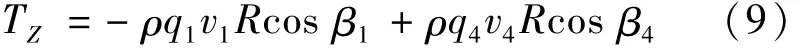
由伯努利方程及前述阀口压降方程可知：以伺服电机正转为例，进回油口处流速方程为

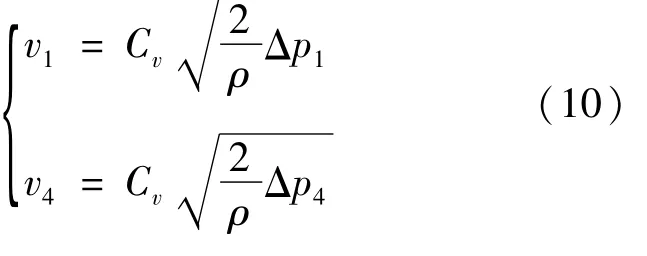
式中：Cv为速度系数；Δp1、Δp4分别为阀口Ⅰ、Ⅳ处压差。

同理，进回油口流量方程分别为

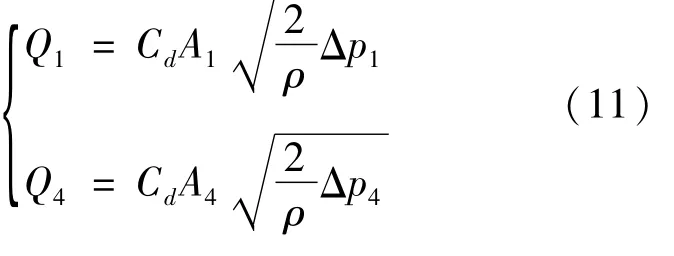
式中Cd为流量系数。

联立式（9）～（11）可知，伺服电机正转时，总稳态液动力矩为

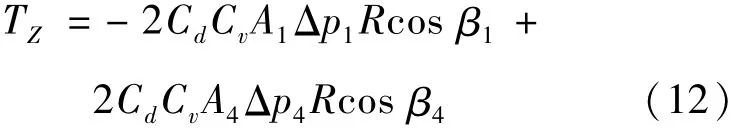
3 结构建模及CFD分析

图6所示为该并联式负载口独立换向阀系统三维结构。在进行Fluent分析之前，需先建立换向阀内部流场模型。参考已建立的换向阀模型，伺服电机正转时，Ⅰ口进油流场如图7所示。同理可得其他阀口的内部流场。

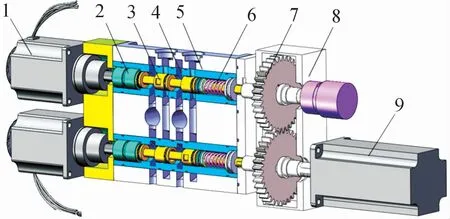
图6 并联式负载口独立换向阀三维结构示意图

利用ICEM CFD对其进行网格划分，整体采用四面体网格，边界采用六面体网格进行细化，以提高网格质量。进行FLUENT仿真时，采用k－ε湍流模型中的RNG子模型，并设置液压油密度为860 kg／m3，动力黏度为0．036 kg／（m·s）。此外，进口和出口边界条件分别设定为速度进口和压力出口。

依据前述模型求解得到的阀口油液流速与阀芯转角关系，并结合已有流场模型，利用FLUENT对其射流角进行仿真分析。其中，伺服电机正转、阀芯轴向位移X1＝X2＝6 mm时，几个特定转动角度下，阀口Ⅰ及阀口Ⅳ处油液流动方向如图8所示。

图7 伺服电机正转时阀芯1进油流场示意图

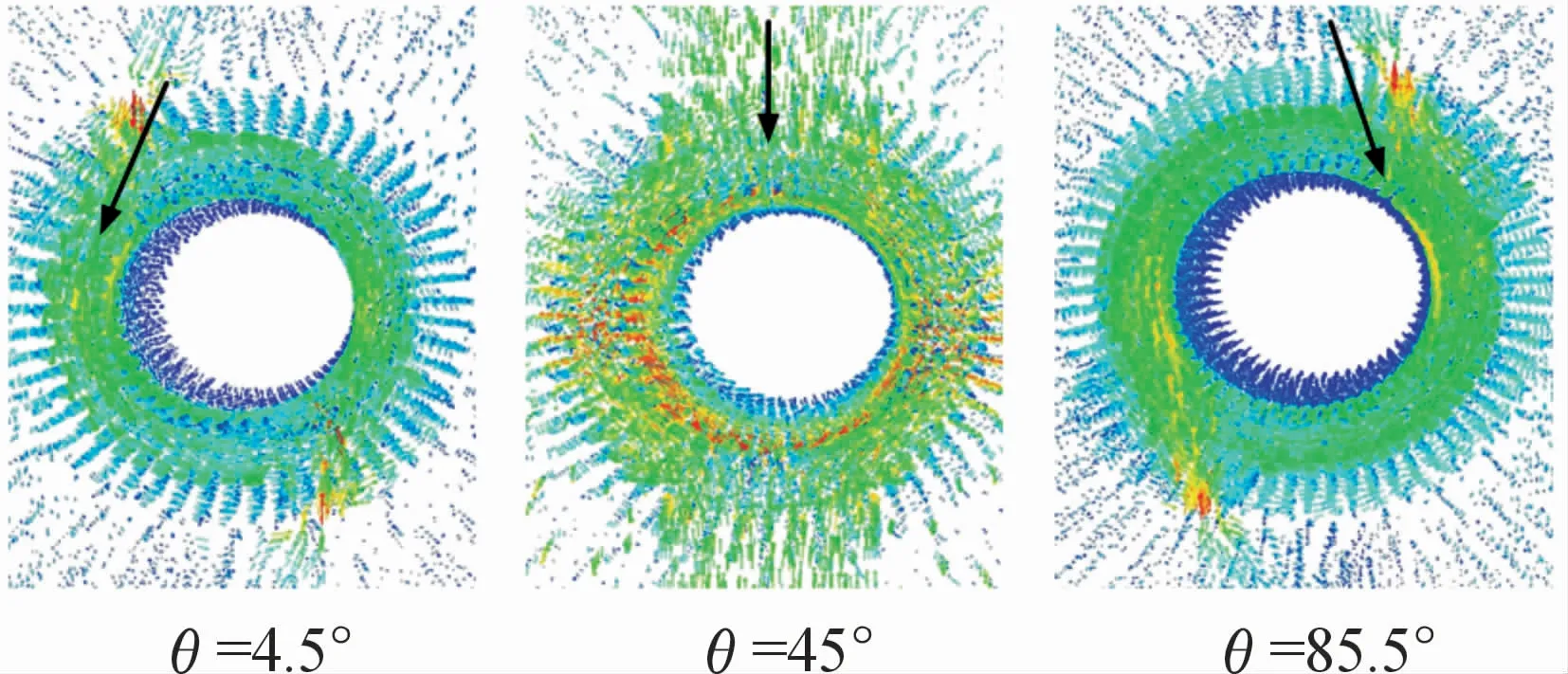
图8 阀口Ⅰ射流角示意图

4 特性分析

4．1 数值模型求解

根据上述模型，利用MATLAB／SIMULINK建立该并联式负载口独立控制换向阀的求解模型，其主要包括3个子模块控制方程，分别为阀口通流面积方程、阀口负载流量方程、阀口油液流速方程。在进行数值求解时，所用的主要参数见表1。

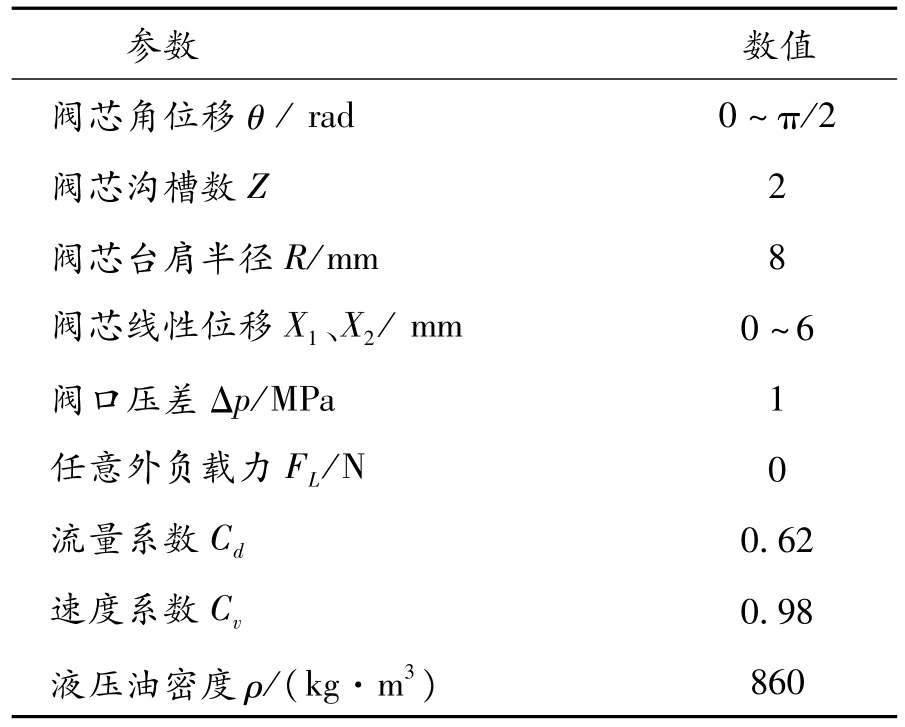
表1 数值求解所用的主要参数

4．2 分析结果

1）阀芯角位移与油液射流角的关系

在伺服电机正转、阀芯轴向位移X1＝X2＝6 mm条件下，若对伺服电机旋转角度单独控制，使阀芯角位移θ以4．5°的步幅从0均匀增加到π／2，则阀口Ⅰ及阀口Ⅳ处射流角如图9所示。由图9可知：在1个完整的阀口旋转开度的变化周期内，阀口Ⅰ及阀口Ⅳ处射流角逐渐增大；阀口通流面积最大时，即阀芯旋转过45°时，阀口Ⅰ及阀口Ⅳ处射流角均为90°，无周向液动力矩；当阀芯角位移关于45°对称时，射流角关于90°对称。

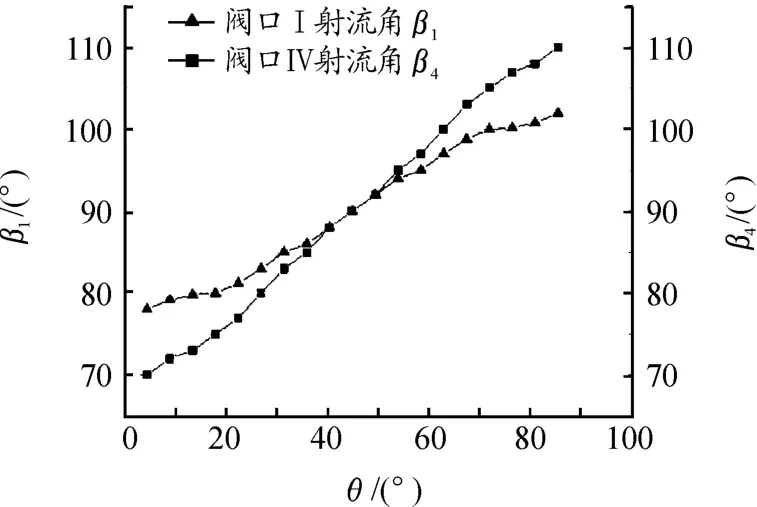
图9 伺服电机正转时时回油口射流角

2）阀芯角位移单独控制条件下液动力矩

在伺服电机正转、阀口压差为1 MPa条件下，若对伺服电机旋转角度单独控制，使阀口转动角度以4．5°的步幅均匀增大，且令X1＝X2＝6 mm，则其进回油口液动力及系统总液动力如图10（a）所示。在阀口压差分别为1、2、3 MPa条件下，其系统总液动力如图10（b）所示，可以看出：阀口压差越大，系统总液动力越大。

在一个完整的阀口旋转开度变化周期内，进油口液动力先减小后增大再逐渐减小，回油口液动力变化趋势与进油口相反。其中，当阀芯角位移在0～π／4时，进油口液动力矩先减小后增大，与对应阀芯旋转方向相反；当阀芯角位移在π／4～π／2时，进油口液动力矩先增大后减小，与对应阀芯旋转方向相同。系统总液动力矩围绕零值波动，且相较于进回油口液动力矩，有明显减小。可知，当阀芯角位移在0～π／4时，系统总液动力先增大后减小，且与伺服电机旋转方向相同；当阀芯角位移在π／4～π／2时，系统总液动力先减小后增大，且与伺服电机旋转方向相反。

3）阀芯轴向位移单独控制条件下液动力矩

在伺服电机正转的条件下，先令伺服电机转过22．5°，而后以0．6 mm的步幅，使二号阀芯位移X2先由0 mm均匀增加到6mm，再由6 mm均匀减小到0 mm，且在这过程中令X1＝6 mm保持不变。则其进回油口液动力及系统总液动力如图10（c）所示。其中，阀芯轴向移动距离在0～6 mm时，阀口轴向开度均匀增大；阀芯轴向移动距离在6～12 mm时，阀口轴向开度均匀减小。

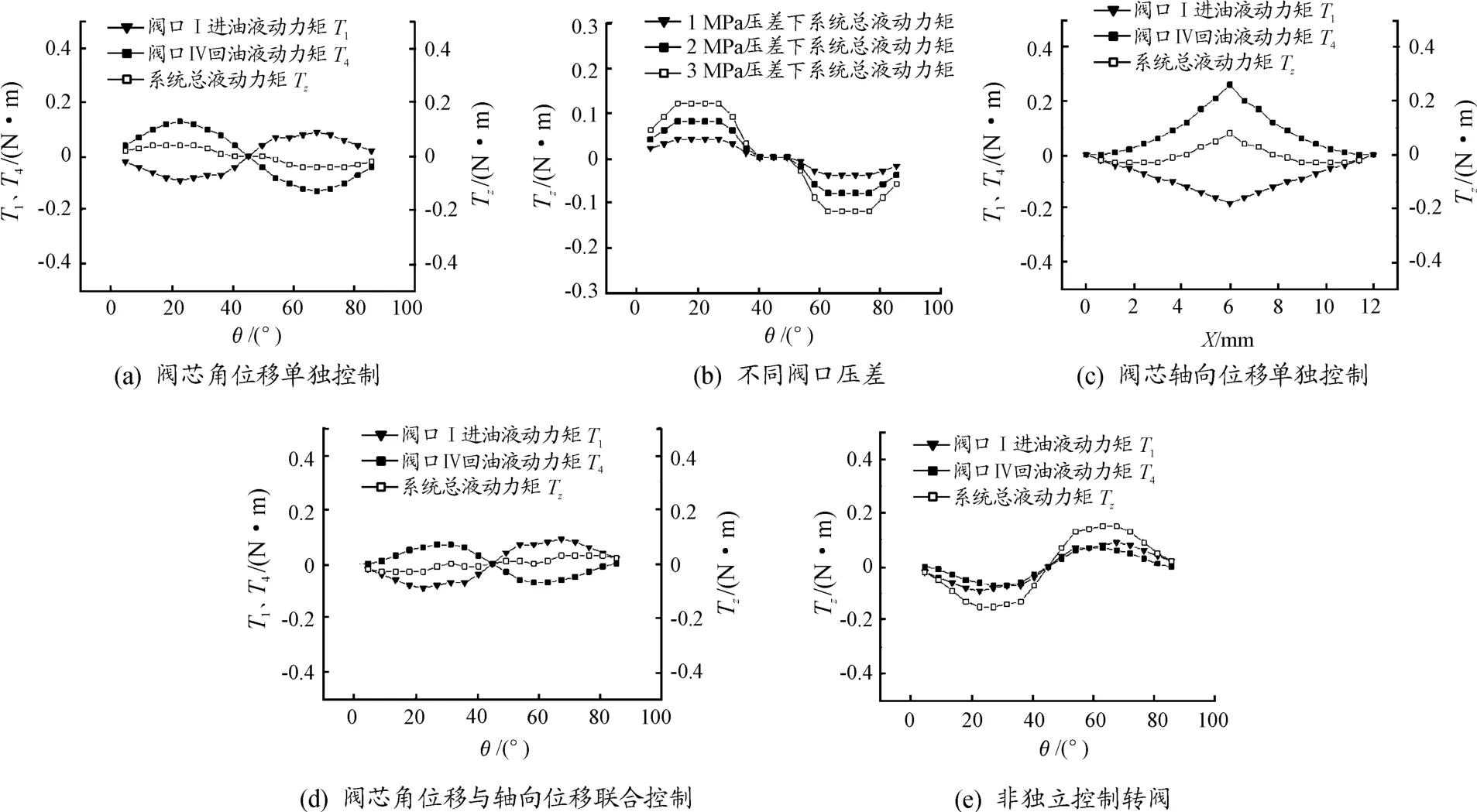
图10 系统液动力矩曲线

从图中可以看出：在一个阀口轴向开度变化周期内，其进油口液动力矩先减小后增大，且在阀口开度最大时，液动力矩最大；回油口液动力变化趋势与进油口处相反，但幅值较大。系统总液动力先增大后减小，相较于进回油口处有明显减小。

4）阀芯角位移与轴向位移联合控制条件下液动力矩

在伺服电机正转、阀口压差为1 MPa的条件下，若对伺服电机旋转角度和直线电机轴向位移进行同步控制，使阀芯角位移θ以4．5°的步幅从0均匀增加到π／2的变化周期内，两阀芯轴向位移以0．6 mm的步幅，先由0 mm均匀增加到6 mm，再由6 mm均匀减小到0 mm。则在此过程中，其进回油口液动力及系统总液动力如图10（d）所示。

从图中可以看出：在一个完整的阀口旋转开度与轴向开度联合变化周期内，其进油口液动力矩先减小后增大，回油口液动力矩变化趋势与之相反。系统总液动力矩围绕零值波动，相较于进回油口液动力矩，已明显减小，且相较于阀芯旋转角位移与轴向位移分别单独控制的2种情况下，联合控制情况下系统的总液动力矩也有减小。

在相同条件下，与负载口独立控制的并联阀相比，非独立控制的转阀［14］，其进回油口液动力及系统总液动力如图10（e）所示。从图中可以看出：独立控制的并联阀相比非独立控制的转阀，其系统总液动力矩明显减小。

5 结论

1）在阀芯旋转位移控制、轴向位移控制以及联合控制的3种工作条件下，该并联换向阀的总稳态液动力矩围绕零值波动，且相比同等工作条件下进回油口液动力矩明显下降。

2）在一个完整的阀口旋转开度变化周期内，油液流经阀口时的射流角呈单调性变化，从而能够通过两阀芯之间适当的配合关系，在阀芯旋转位移和轴向位移联合控制下，降低系统总稳态液动力矩。

3）双阀芯并联式负载口独立控制换向阀，可以适应不同的工作场合，且能够有效地降低换向阀工作时的总稳态液动力，对于此类换向转阀的设计具有指导意义。