基于转矩－转速模式切换的电机控制研究

罗玉涛，许晓通，许 轲

（华南理工大学 机械与汽车工程学院，广州 510641）

随着电动机应用场景的日益广泛，对转矩和转速2种控制模式在线切换的需求日益强烈。例如，在安装有机械式自动变速器的纯电动汽车中，采用转速控制模式可快速消除换挡过程接合套与目标挡位的接合齿圈的转速差，而一般行驶过程则采用转矩控制更为合适。换挡的转速同步过程要求驱动电机控制系统适时地切换控制模式［1］，因此研究电机转矩－转速控制模式的在线切换具有实际意义及实用价值。

对转速控制的研究由来已久，相关学者提出了滑模控制［2］、自适应控制［3－4］、神经网络控制［5］等提高调速过程快速性和稳定性的方法，但实际工程应用中，仍以PI控制为主。对电机模式切换过程的研究较少，傅洪等［6］采用双滑模直接转矩控制方法控制转矩，同时利用PID控制器形成转速闭环，仿真结果显示在切换点处转矩急速增加，但其研究中未对此做进一步分析；C．H．YU等［7］采用滑模控制算法调节转速，发现切换后转速响应更为快速平稳，但未对电机模式切换过程带来的影响进行考虑。

本文中以PMSM为控制对象，基于传统的PI双闭环电机控制方法分析了电机模式切换过程，提出切换时系统电流冲击大的问题。为解决该问题，在电机模式切换过程中引入一段过渡过程，过渡过程中仍以电磁转矩为控制目标，通过对目标转矩的设计，使系统转速达到目标转速的同时电磁转矩等于负载转矩。此时，将电机控制模式切换到转速模式，将系统转速稳定在目标转速，完成调速过程。为获得负载转矩，设计Luenberger观测器实时观测负载转矩，以保证切换过程快速而平稳。

1 电机控制模式切换分析

1．1 传统电机控制模式切换系统

传统的电机模式切换控制系统基于双闭环矢量控制算法［8］，其结构见图1。

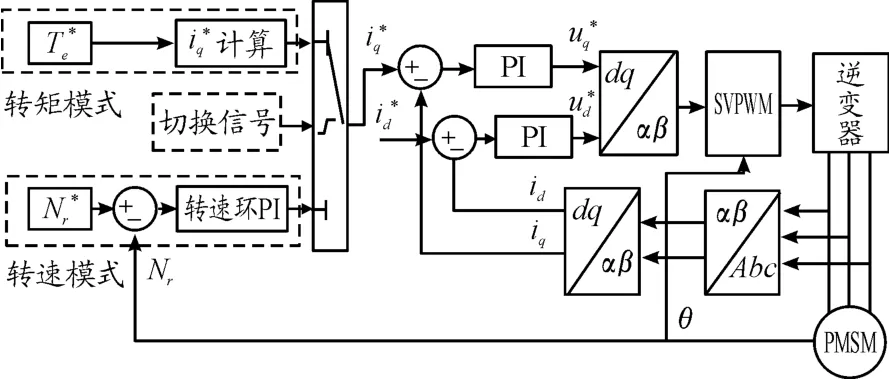
图1 传统电机模式切换控制系统结构框图

转矩控制模式下，可通过dq坐标系下PMSM电磁转矩方程计算目标转d轴目标电流目标电间的关系［9］。

式中：np为电机极对数；ψf为永磁体磁链；Ld和L分别为d轴和q轴电般由弱磁程度决q定，在非弱磁区，可采的控制方案。

转速控制模式下，将目标转速与目标转矩建立联系，进而控制转速变化，采用PI控制器实现该过程。PI控制器参数的设计基于运动平衡方程［10］：

式中：Tm为等效负载转矩，Tm＝Tf＋TL＋Bωm；Tf为静态摩擦转矩；TL为外部负载；B为迟滞阻尼系数；J为电机转动惯量；ωe为转子电角速度。

1．2 控制模式切换过程分析

由转矩控制模式切换到转速控制模式时，以降速为例，其示意切换过程转速化见图2。

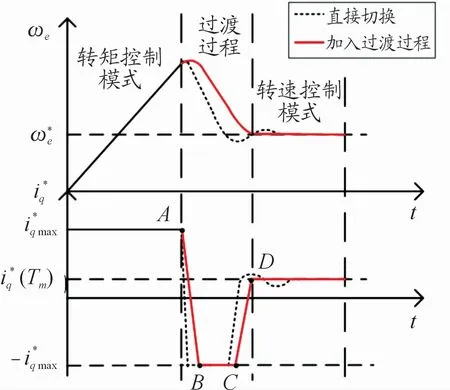
图2 引入过渡模式曲线与直接切换曲线

传统方法采用直接切换的方式，在A点接收到切换信号后，直接将控制模式切换到转速控制，转速环PI控制器瞬时参与控制，其输出为：

式中：R为绕组电阻；ψd为d轴磁链。

产生电流冲击的原因是切换瞬间较大转速差引起的电磁转矩需求与当前电磁转矩差距过大。目标转速与当前转速差越大，电流冲击越大。因此，考虑将切换点从A点后移至D点，并在系统转速达到目标转速时进行电机模式切换，即可降低切换点处的电流冲击。同时，注意到若在切换前后电磁转矩与负载转矩不一致，则系统会快速调节电磁转矩，引起转速在目标转速上下波动。转速达到目标转速时，电磁转矩也恰好等于目标转矩，则可消除该波动，提高转速响应快速性和稳定性。

基于以上分析，提出一种引入过渡过程的电机模式切换方法，接收到切换信号及目标转速后，控制系统进入过渡过程。该过程中，仍采用转矩控制，通过对目标转矩的设计，使电机转速达到目标转速的同时电磁转矩与负载转矩恰好相等，此时切换到转速模式以稳定转速。切换后，需求转速／转矩与实际转矩／转速相同，系统可稳定进行模式切换。同时由式（3）可知，切换点处PI控制PI控制器输出端。构建引入过渡过程的电机模式切换系统结构，见图3。

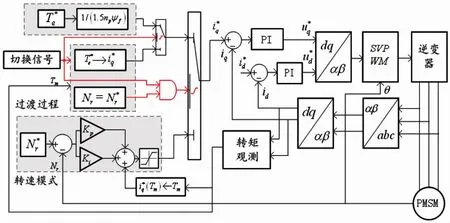
图3 引入过渡过程的电机模式切换系统结构框图

2 过渡过程控制

过渡过程仍采用转矩控制，设计重点为确定AB段、BC段和CD段的目标转矩。为降低控制复杂度，在三段内保证目标转矩变化率不变，为缩短响应时间，BC段应一直保持最小电磁转矩（升速时为最大电磁转矩）。按降速过程重点分析AB段和CD段目标转矩设计，升速过程分析方法与之相同。

2．1 AB段目标转矩控制

直接切换时，目标转矩瞬时突变会引起电流冲击。在引入过渡模式的切换方法中，为避免电流冲击，需合理设定目标转矩的变化速率。

电流冲击的主要影响在于会引起较大感应电动势，造成对电机和逆变器的冲击。当反电动势大于母线电压时，会对逆变器造成反向冲击，因此以母线电压为依据设计目标转矩变化率，在不考虑弱磁情况下，两者关系为：

式中：Udc为母线电压；R为绕组电阻；Lq为q轴电感；ωe为转子电角速度；ψf为定子磁链。

整理式（5）得：

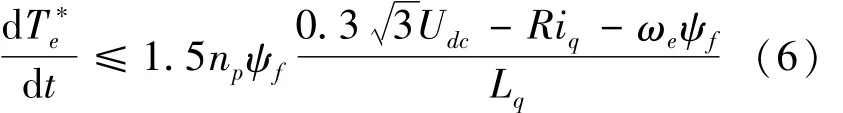
可见，通过转子电角速度ωe即可匹的允许值。由于CE段历时较短，起始点和结束点转速变化不大，因此可采用C点转速匹配CE段目标转矩变化率d Te／d t。为降低转矩变化率达到峰值带来的冲击，在仿真及试验中，取峰值的90%控制转矩变化率。

2．2 CD段目标转矩控制

CD段目标转矩的设计除设计变化率外，还需确定C点对应时刻，即目标转矩从极限值回落的时间点。目标转矩变化率可按2．1节所述方法设计。

转矩回落时间点的设计目标为保证转速达到ω时，转矩恰好达到T。若不考虑弱磁，即i＝emd0，由式（1）和式（2）可得C点过渡到D点过程中，转速和转矩的关系：

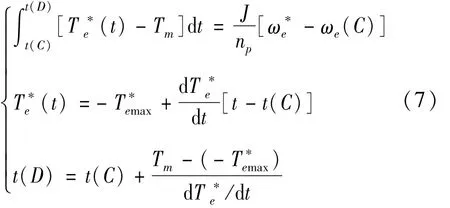
式中：t（C）和t（D）分别为C点对应时刻和D点对应时刻；C点转子电角速度。为CD化率。

整理式（7）可得：

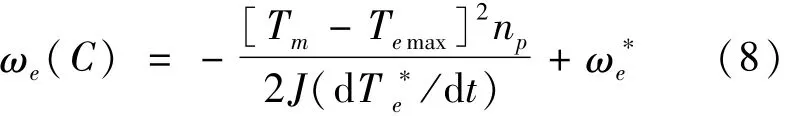
由式（8）可知：只需确定Tm即可确定C点转即在转速达开始的速率改，可实现当转速达目标转矩恰好达到Tm。因此，问题转换为确定负载转矩。

假设转速同步过程中，负载转矩变化很小，于是在进入过渡模式后即可采用算法观测的方式来得到负载转矩，同时可节省转矩传感器带来的硬件成本。负载转矩观测的常用方法有滑模变结构法、卡尔曼滤波法和Luenberger观测法［11－14］。Luenberger观测法复杂度较低，响应速度快，精度较高，因此本文中设计Luenberger转矩观测器观测负载转矩。

2．3 转矩观测器设计

2．3．1 能观性分析

通过Luenberger方法观测系统变量的前提是该系统必须完全能观［15］。PMSM的转矩平衡方程如式（2），以此为基础建立被测系统的状态空间方程。将电磁转矩Te定义为输入，电角速度ωe和负载转矩Tm定义为状态变量，ωe同时定义为系统输出，则被观测系统的状态空间方程为：

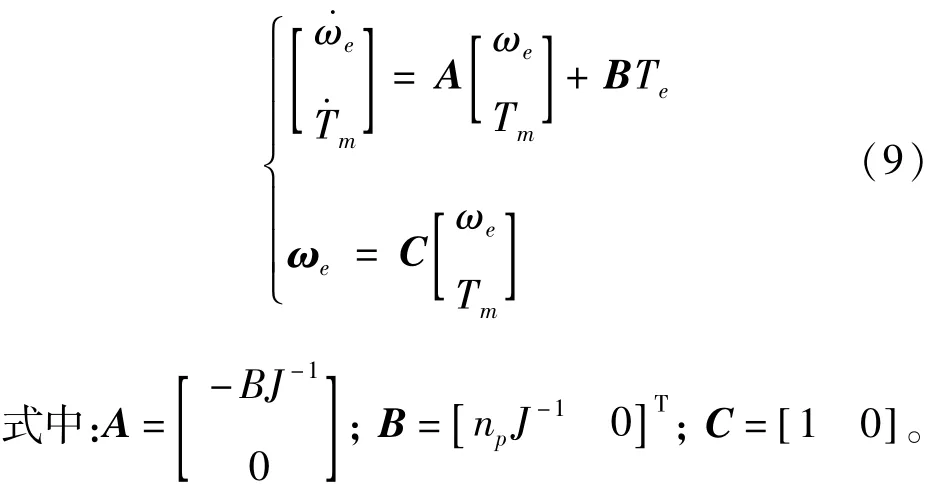
上述系统满足齐次叠加性，因此可看作线性定常系统，其完全能观的充要条件是其能观性矩阵为满秩，系统的能观性矩阵为：

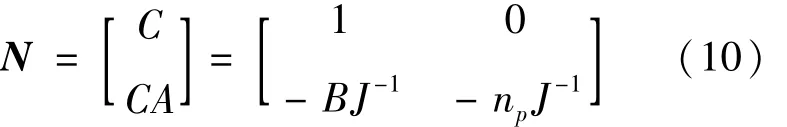
可见，系统能观性矩阵的秩为满秩，因此本系统是完全能观的。

2．3．2 观测算法设计

被测系统在能观的基础上可由状态空间方程建立Luenberger负载转矩观测器，状态空间方程为：

根据式（11），构建Luenberger负载转矩观测器的结构，如图4所示。

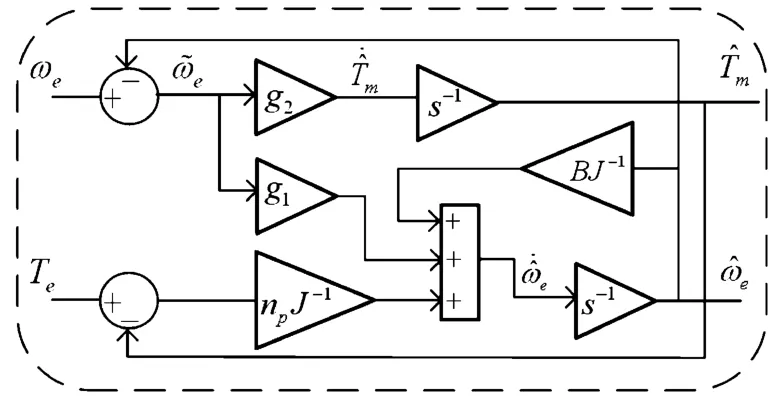
图4 Luenberger负载转矩观测器结构框图

2．3．3 反馈矩阵设计

上述设计的Luenberger转矩观测器是一个闭环系统，通过矩阵G进行误差反馈。该矩阵的设计直接影响观测状态向实际状态趋近的快速性和稳定性。

引入系统状态误差：

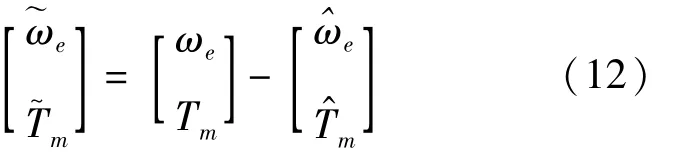
用式（12）减去式（11），得到状态误差方程为：

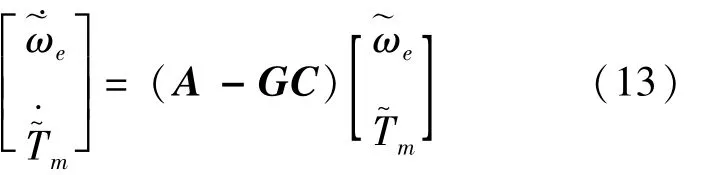
解该方程得：

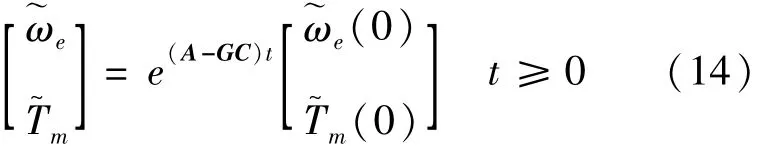
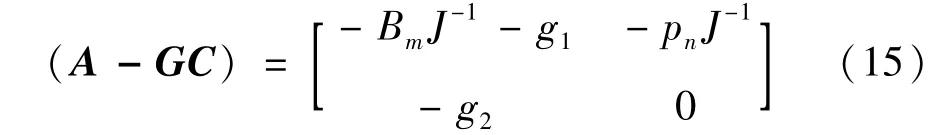
其特征方程为：

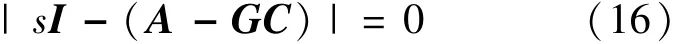
将式（15）代入式（16）可得：

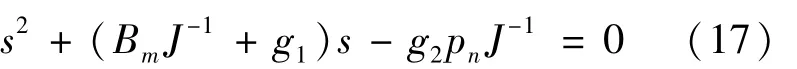
为使（A－GC）具有负实部，则式（17）需要具有位于复平面左侧的根，因此不妨设该式有2个小于0且相等的根α1和α2，有α1＝α2＝α＜0。于是式（17）可化简为：

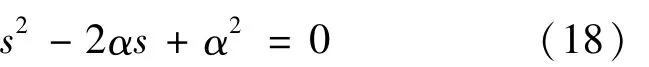
比较式（17）和式（18），可得：

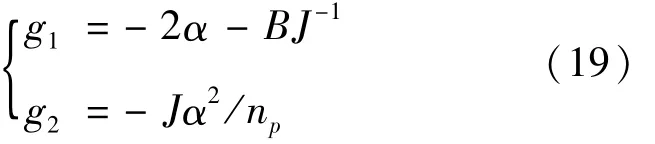
α＜0时有：

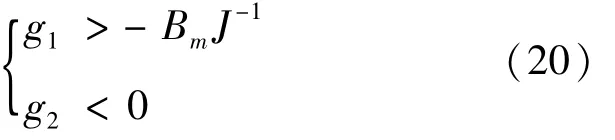
3 仿真验证

3．1 负载转矩观测系统仿真

在Simulink仿真平台中按图4所示结构搭建Luenberger转矩观测器模型，并结合电机控制系统模型进行仿真，使负载转矩分别按方波形式和三角波形式变化，结果如图5所示。在方波负载下，观测器响应时间为6 ms，最大超调为0．013 N·m，即1．3%，且稳态过程没有明显波动。在三角波负载下，观测器在9 ms内可稳定跟随实际负载转矩，但存在0．05 N·m的误差，跟随过程中无明显落后和超调。可见所设计的Luenberger负载转矩观测器能快速跟踪实际负载的变化，且稳定性好。

3．2 基于电机模式切换的转速控制过程仿真

为验证本文中所提出的引入过渡过程的电机模式在线切换方法的有效性，基于某款电动汽车用两挡变速箱参数［16］模拟换挡过程中升速和降速的转速控制过程，1挡传动比为3．15，2挡传动比为1。降速时，电机转速由3 000 r／min切换到952 r／min。升速时，转速由900 r／min切换到2 835 r／min。同时，基于2．1节和2．2节对转矩变化率的分析，可确定转速在接近2 835、3 000 r／min时，转矩变化率应分别保持在512、501 N·m／s内；转速在接近900、952 r／min时，转矩变化率应保持在1 501、1 498 N·m／s内。基于以上参数对传统切换方法和引入过渡模式的切换方法在Simulink平台上进行仿真。电机模型参数及逆变器模型参数见表1。

图5 方波及三角波负载下负载转矩波形

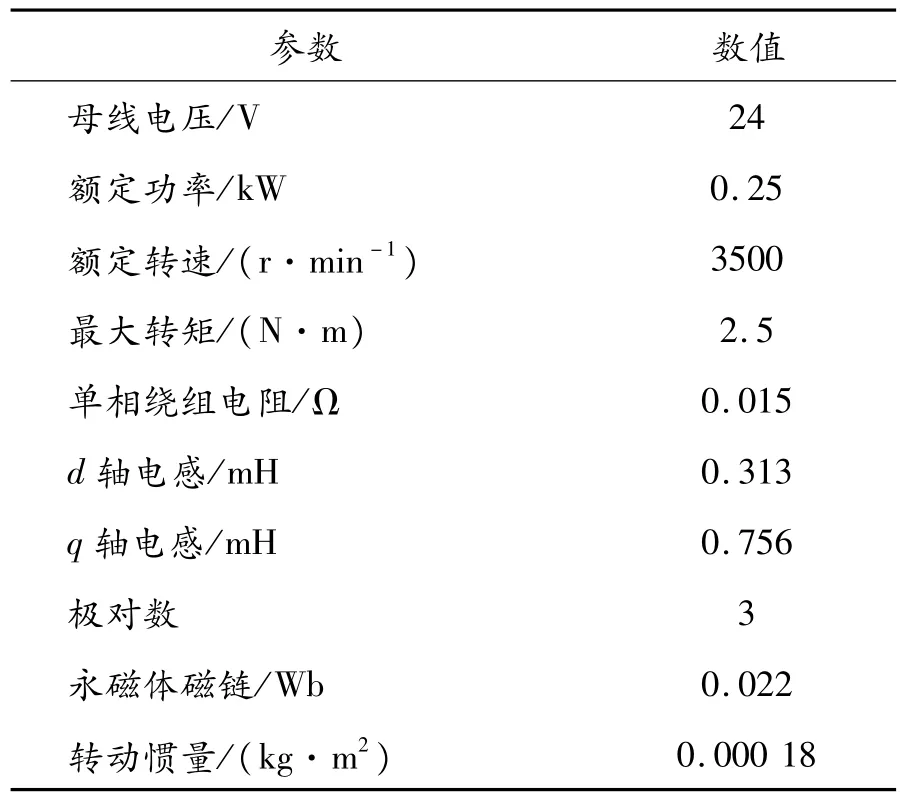
表1 电机模型参数

升速过程中的转速响应曲线和转矩及d iq／d t变化曲线分别如图6、7所示。电机启动后，以1 5 N·m转矩升速；A点处，系统接收到切换信号；直接切换方法下，该点处直接切换到转速控制，引入过渡过程后，进入A－D段。AB段控制转矩从1．5 N·m上升到2．5 N·m，过程中目标转矩按1 501 N·m／s变化；BC段，以最大转矩2．5 N·m升速，直到转速到达按式（6）计算得到的ωe（F）；CD段控制转矩从2．5 N·m下降到负载转矩，过程中目标转矩按512 N·m／s变化。D点处由转矩模式切换到转速模式。定义稳态误差为±5%，在直接切换和引入过渡模式切换方法下，升降程转速稳定时间、超调量及d iq／d t值见表2。

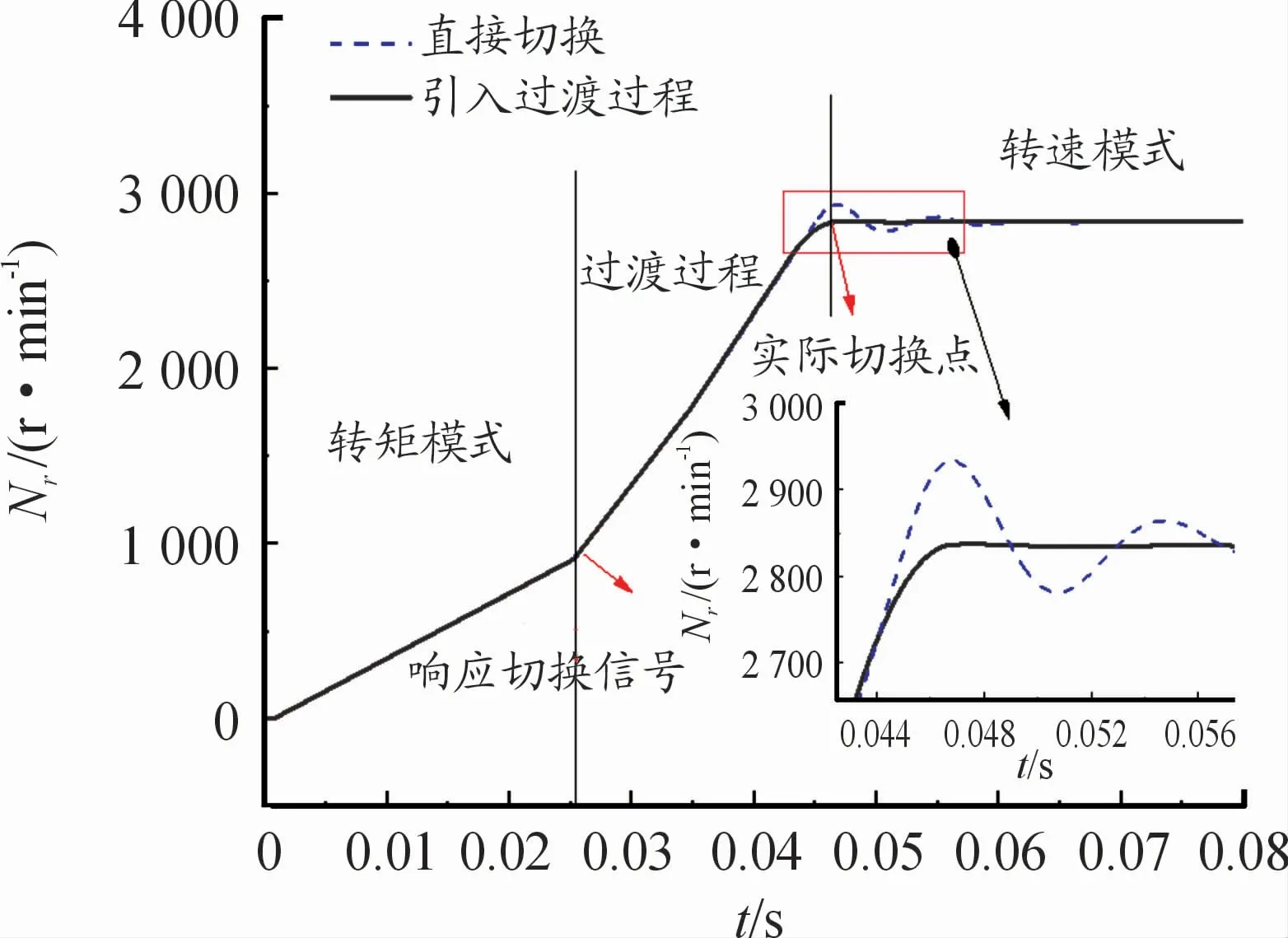
图6 升速过程2种方法转速响应曲线

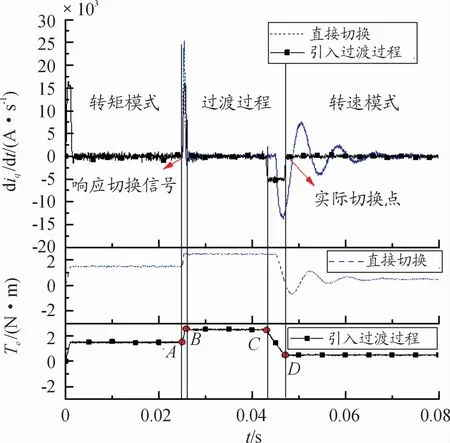
图7 升速过程2种方法转矩及iq变化率

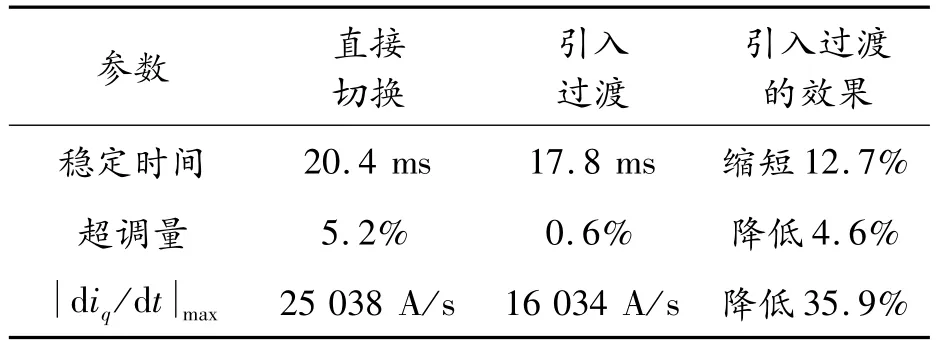
表2 升速过程2种方法结果

降速过程中的转速响应曲线和转矩及d iq／d t变化曲线分别如图8、9所示。降速过程与升速过程类似，不同之处在于AB段的控制转矩从2．5 N·m下降到 －2．5 N·m，过程中目标转矩按－501 N·m／s变化；BC段中，以 －2．5 N·m转矩降速，直到转速到达按式（6）计算得到的ωe（F）；CD段控制转矩从－2．5 N·m上升到负载转矩，过程中目标转矩按1 498 N·m／s变化。2种切换方法下的降速过程控制效果见表3。

图8 降速过程2种方法转速响应曲线

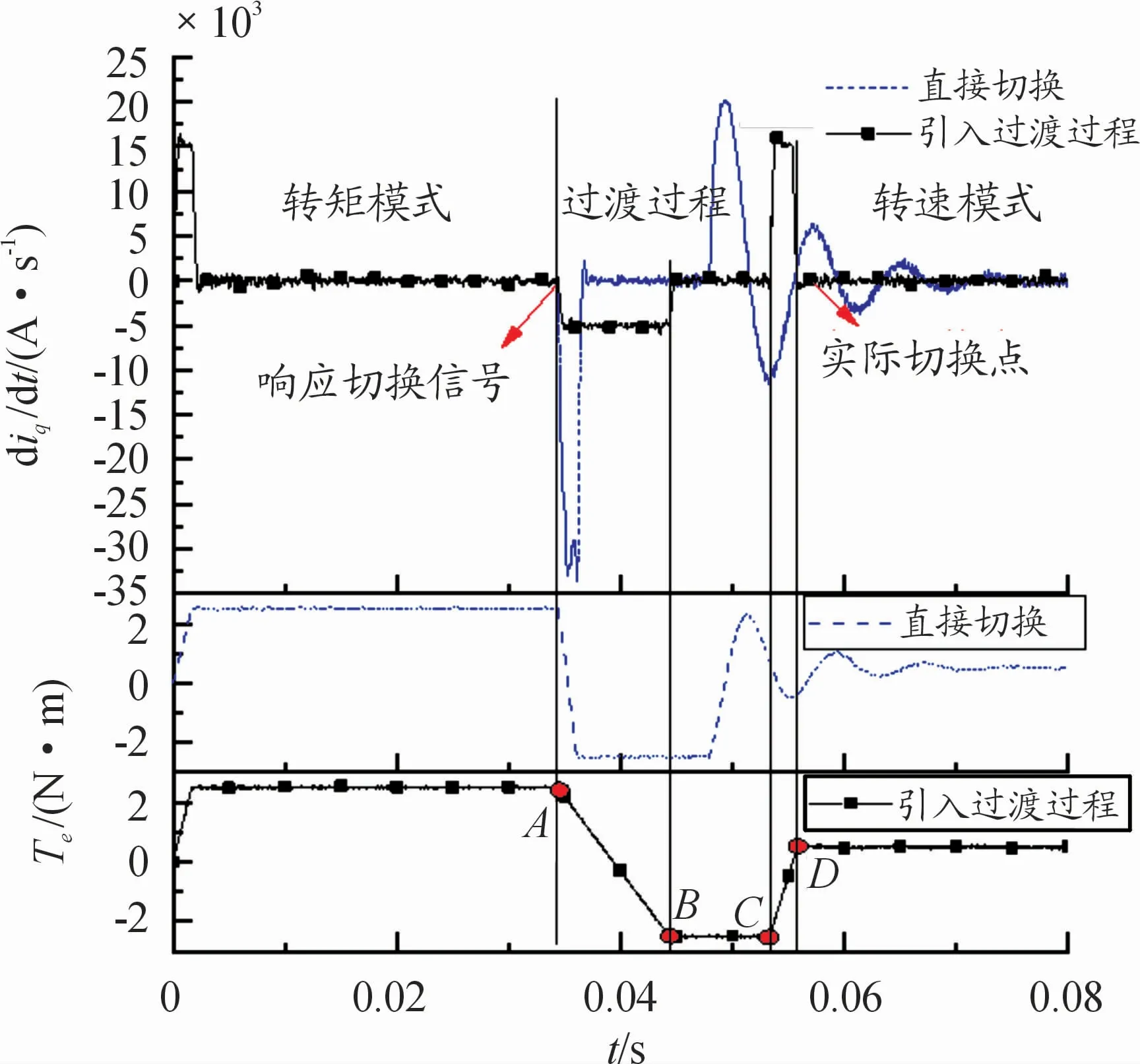
图9 降速过程2种方法转矩及iq变化率

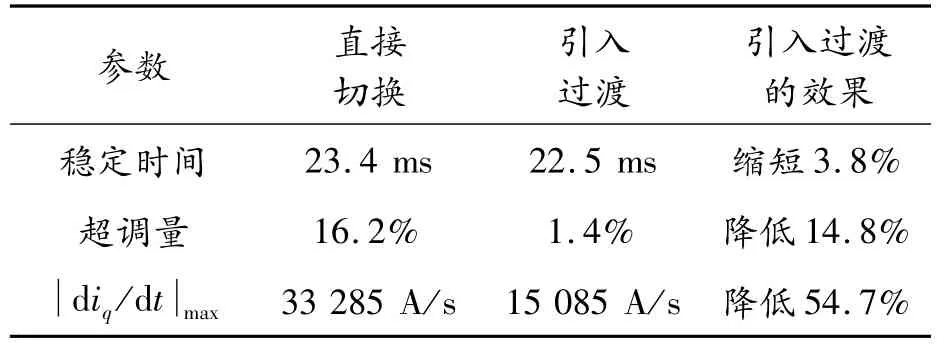
表3 降速过程2种方法结果

4 试验验证

为验证所提方案的正确性，基于英飞凌TC275微处理器搭建永磁同步电机驱动控制试验平台。系统时钟频率为150 MHz，脉宽调制逆变器周期频率为10 kHz，利用TC275的CAN模块上传试验数据。试验平台实物图如图10所示。

图10 试验平台实物图

试验所用电机参数与仿真保持一致，ABCD点电机状态也与仿真设置相同。升速与降速过程电机转速、电磁转矩和d iq／d t见图11、12所示。结果表明：引入过渡过程后，电机实际响应与仿真的趋势保持一致，升速和降速阶段，相较于直接切换，采用引入过渡过程的切换方法时转速稳定时间分别缩短15．7%和3．5%；超调量分别下降4 2%和12．1%；d iq／d t分别降低12．8%和44．1%。总结上述结果可以发现：切换信号到来后，若需求转矩与当前转矩差距小，则引入切换过程降低d iq／d t和减少超调量的效果不甚明显，但降低转速稳定时间的效果较好；若切换信号到来后，需求转矩与当前转矩差距大，则引入过渡过程可显著降低d iq／d t和超调量，但只能少量提高转速稳定速度。

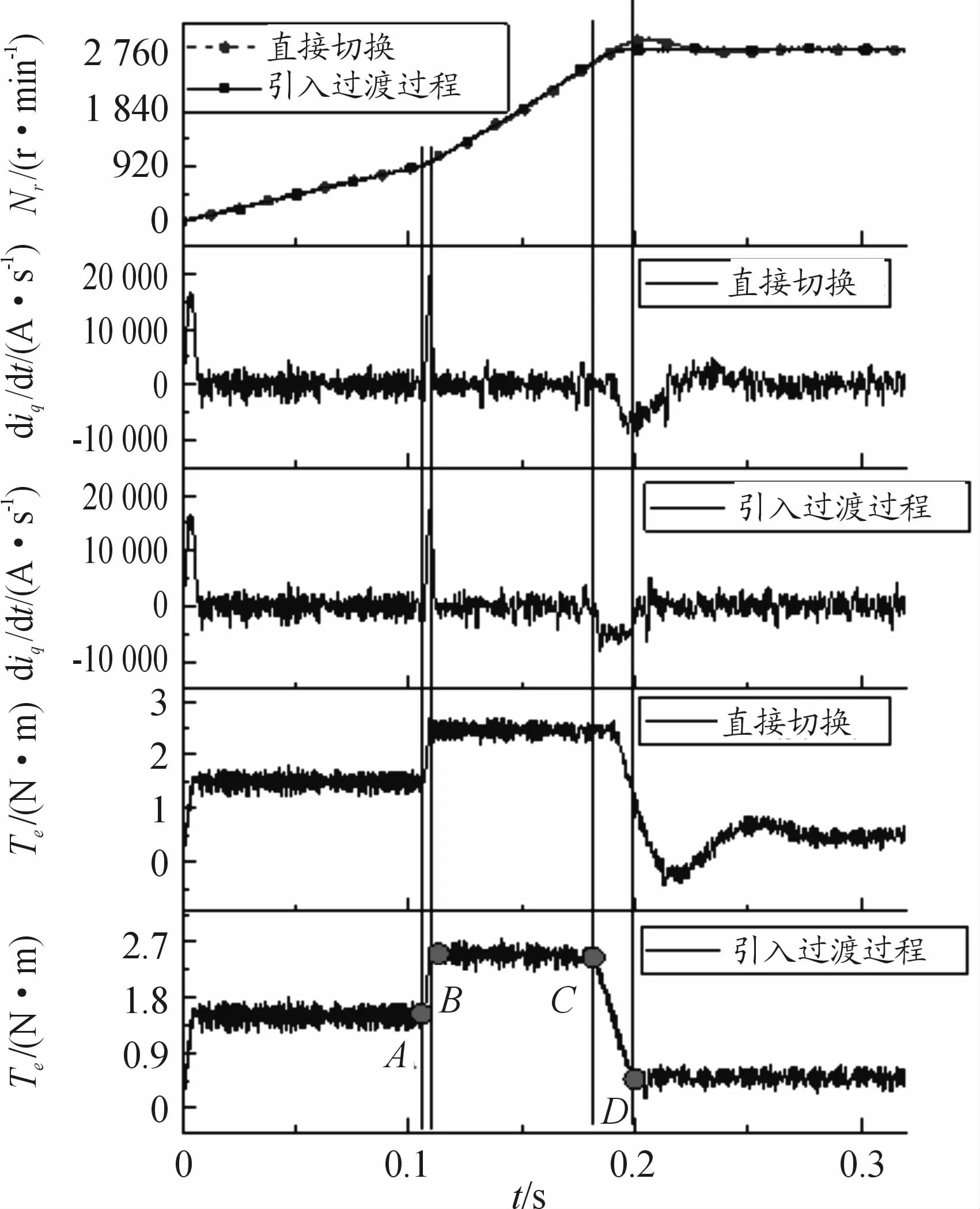
图11 升速过程2种方法试验结果

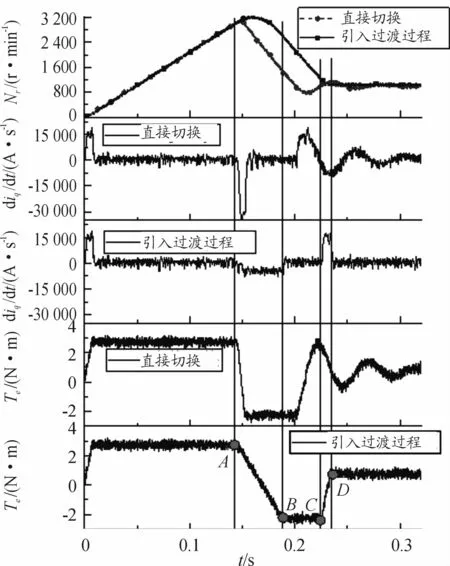
图12 降速过程2种方法试验结果

5 结论

1）引入过渡过程的电机模式切换方法切实可行，且能缩短调速时间、减少超调量，并有效降低切换过程中的电流变化率。

2）切换信号发出后，需求转矩与当前转矩差距越大，引入过渡过程的电机控制模式切换方法提高调速响应速度能力越差，但降低电流变化率和减少超调的效果越明显。