基于分层式控制器的纯电动汽车车距控制研究
张新锋,陈建伟,王奥特
(1.长安大学 汽车运输安全保障技术交通行业重点实验室,西安 710064;2.长安大学 汽车学院,西安 710064)
近年来,随着交通拥堵和环境问题的日益突出,智能化和电动化成为汽车领域的研究热点。纵向车距控制系统作为智能车辆的重要研究内容,是实现全自动驾驶的基础[1]。目前的研究主要包括车距控制算法以及跟车间距策略,其中常见的控制算法有经典PID控制[2]、基于二次车距模型的非线性解耦控制律[3]、基于固定车距模型的滑模变结构控制律[4]以及搭建车间时距模型的线性二次型控制律[5]等;跟车间距模型是实现车辆安全行驶的重要组成部分,主要有安全跟随距离(TGFD)模型[6]、最小车距安全距离模型[7]等。通过分析,目前的控制器大多采用单一的智能控制算法,对适用于多工况的纯电动汽车车距控制系统的研究还比较少,并且缺少针对不同车速的可变安全距离模型。
基于此,建立了纯电动汽车动力学模型,针对不同工况,搭建了一种可变安全距离模型,并采用分层式控制结构,将控制器分为顶层控制器和底层控制器,基于Carsim/Simulink联合仿真平台,实现智能车辆在起停工况、定速巡航、距离保持工况下的车距控制。
1 纯电动汽车动力学建模
纯电动汽车的车距控制研究需要搭建整车动力学模型,基于Carsim传统燃油车模型,在Simu link建立驱动电机模型,导入到整车模型中。
1.1 驱动电机的选取
目前,车用驱动电机主要有直流电机、交流异步电机、开关磁阻电机和永磁无刷直流电机等。其中,直流电机功率密度低、转速低、效率较低;交流异步电机发热较为严重,控制比较复杂;开关磁阻电机电磁转矩脉动较大,低速电流波动大,控制电路复杂[8];而永磁无刷直流电机转速高、体积小、控制简单并且在低转速时输出较大转矩。因此,选取永磁无刷直流电机作为车用电机。
1.2 驱动电机动力参数确定
电机提供车辆行驶的动力,为满足车辆加速性能、最大速度和最大爬坡度,应选取合适的功率、转矩和转速等参数[9]。
根据表1的车辆性能指标,结合Carsim中A级车的参数,对驱动电机动力参数进行匹配计算,本文选取额定功率PExtra取值为22 kW。最大功率Pm=55 kW。取电机最大转矩Tmax=200 N·m。额定转矩Textra=80 N·m。电机最大转速nm=6 200 r/min,额定转速ne=2 700 r/min。

表1 整车性能指标
1.3 驱动电机数学模型
对驱动电机进行数学建模,简化电机工作过程和自身结构中铁芯饱和、剩磁干扰的影响;忽略电机边缘磁通量的影响;并且假设定子上的三相绕组的安装方式是对称星状,即电机的线电流等于各绕组相电流。
因此电压方程为

式中:L和M 为定自绕组自感系数和互感系数;ei、ii和ui为相电动势(i取A、B、C)、相电流和相电压;R为绕组电阻。
转矩方程和目标转矩方程为

式中:Te和Tm为电磁转矩和目标转矩;i和im为电机的输入电流和目标电流;K为电磁转矩系数;ω为电机转角速度。
运动方程为:

式中:T为机械负载转矩;J为转动惯量。
因PI控制控制精度高且控制方式简单,对电机的控制采用简单的PI控制。电机工作的目标电流im和负载两端的电压u分别为:

式中:Kp1、Kp2和Ki1、Ki2分别为目标电流和负载电压的比例系数和积分系数。
当电机处于工作状态时,可以将其视为一相是断开的,假设A相断开时的负载电压为

式中,Ke为反电动系数,Keω=2eE。
根据上述数学模型,在Simulink中得到电机模型。
1.4 整车动力学模型
对传统的动力传动装置进行改装,切断发动机模型的动力输入,通过外部接口连接电机模型实现电机驱动,其他模型参数均采用某款A级纯电动汽车默认值,如表2所示。

表2 车辆部分参数
2 安全距离模型的搭建
安全距离模型影响整个车距控制系统的控制效果,本文中对典型的安全距离模型进行改进,提出了一种考虑极端条件和制动器起作用时间的可变安全距离模型。
2.1 典型安全距离模型
1)固定安全距离模型。一种预先设定的距离模型,根据本车车速选取相对应的安全距离。该算法没有考虑驾驶员特性和前车行驶状态,缺乏灵活性[10]。
2)自由滑行时间模型。以预先设定好的滑行时间作为参数,vS为自车车速,tS为自由滑行时间,模型[11]可表示为:

式中:DS为安全距离;L为停车间距,常数L决定安全距离的取值。对于复杂工况(起步-停车等),模型精度较差。
3)驾驶员预估安全距离模型。根据驾驶员的驾驶经验,估计自车与目标车辆的相对速度与相对距离,模型[12]可表示为:

式中:vC为两车相对速度;tC为估计时间;af为跟踪车辆减速度;e为两车完全停止时的最小安全距离。该模型中m的取值取决于驾驶员个人主观感受。估计时间tC的确定也较为困难,导致精确性不够。
4)车间距保持安全距离模型。该模型也是通过预先设定好的参数对安全距离进行计算。没有考虑到VCU(vehicle control unit)发出指令到车辆开始减速的时间,容易在极端情况下发生追尾碰撞。
综上所述,安全距离模型的建立必须考虑极端条件和制动器起作用时间,确保智能车辆安全行驶。
2.2 可变安全距离模型
安全距离模型直接决定自车前车之间的最小行车距离[13]。根据测量到的两车间的实际距离以及安全距离,对车距进行精准控制。安全距离模型考虑本车的行驶状态、制动器起作用时间的同时,还需要跟踪车辆的实时行驶信息。基于此,本文采用考虑了制动反应时间,建立的可变安全距离模型:

式中:S为安全距离;vC、vT分别为自车车速和前跟踪车辆车速;t为控制器反应时间;d为两车停止时的最小安全距离;amin为自车的最小加速度。其中,参数t、d、amin根据研究车辆的不同而变化。本文中分别取制动器反应时间t为0.8 s,最大制动减速度amin为 -5.5 m/s2,两车停止时的最小安全距离约为本车车长[14],d取值为3 m。将其代入式(10),可得安全距离模型:

在极端情况下,即前车制动时,两车最有可能发生追尾碰撞,此时前车速度vT为零。根据式(11),此时的安全距离模型表示为:

3 控制器的设计
采用分层式控制结构,将控制器分为顶层控制器和底层控制器。基于线性二次型最优控制理论设计顶层控制器,输出自车的期望加速度。底层控制器通过驱动/制动控制切换策略,将期望加速度进行分配,对车辆的驱动和制动进行相应控制,达到车距控制的目的。
3.1 基于LQR的距离保持顶层控制器
LQR(linear quadratic regulator)最优控制算法可表示为线性系统,并且易于构成闭环最优控制,其性能指标是由对象状态和加权值组成的二次型函数。基于LQR设计的距离保持顶层控制器利用车载传感器探测到的距离和速度信息以及搭建的安全距离模型,可以得到自车的期望加速度。
根据车载传感器探测到的信息可以得到自车和前车的相对速度和加速度的传递特性关系

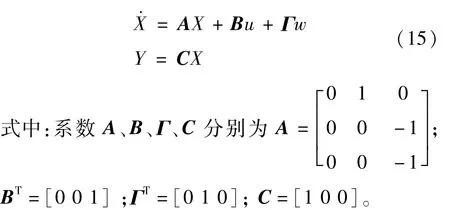
其中,控制误差为自车和前车的期望距离与实际距离的差值,表达式为:

式中:e(t)为控制误差;ddes(t)、ζ(t)分别为两车的期望车距和实际车距。取控制器性能指标J:

式中:qe、ru分别为控制误差和控制量的加权值。通过最优控制,使性能指标最小。根据最优跟踪问题的求解方法可以将公式表达为:

式中,k1、k2、k3为状态反馈系数,控制器的性能由qe、ru确定,其中跟踪性能由qe确定,控制器的控制能量消耗由ru确定,即以较小的加速度变化对前车进行跟踪。
根据车辆的行驶特性,假设qe、ru正定,即qe>0,ru>0,通过黎卡提代数方程的求解,取误差加权值qe=1,控制量加权值ru=7。可以得到反馈系数k1、k2和k3分别为0.216 2、1.624 3和0.682 4。根据式(18)可求得期望加速度:
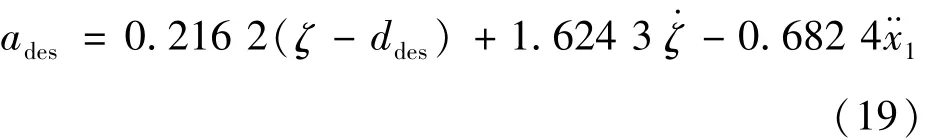
为了保证乘坐舒适性,需要对期望加速度进行控制。参考目前车辆加速度取值范围,本文的速度大小为[-5.5 3.5]m/s2。在Simulink中仿真过程如图1所示。
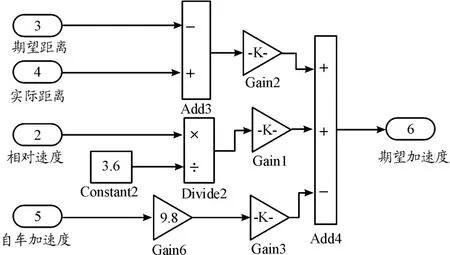
图1 线性二次型最优控制理论Simulink仿真过程示意图
3.2 定速巡航顶层控制器
当目标车速大于巡航速度或者两车间距大于期望间距时为定速巡航模式,基于PID控制理论设计出定速巡航控制器,使车辆按照设定的速度稳定行驶。
es(t)为设定的巡航速度vdes和车辆实际速度vact之差:

将速度误差es(t)作为控制器的输入,期望加速度ades作为输出,控制车辆按照期望加速度行驶。PID顶层控制器的比例系数取值为1.6,积分系数取值0.4,微分系数取值0.01。仿真过程如图2所示。

图2 PID控制器Simulink仿真过程示意图
3.3 驱动/制动切换策略
由顶层控制器得到的期望加速度为依据,对车辆采取驱动或制动控制,考虑到车辆的经济性和乘坐舒适性,两者不能频繁切换,因此应设定一个过渡区域。根据实践经验,过渡区域宽度为2Δh,Δh一般为0.1 m/s2。由期望加速度ades制定出驱动/制动的切换策略。如下:
1)当ades≥a+Δh时,对自车进行驱动控制,无制动力作用。
2)当a-Δh<ades<a+Δh时,为过渡区域,不对驱动和制动进行切换。
3)当ades≤a-Δh时,对自车进行制动控制,无驱动力作用。
依据上述驱动/制动切换策略,可以把顶层控制器得到的期望加速度合理地分配给驱动模块或制动模块。切换策略在Simulink上进行仿真,其过程如图3所示。

图3 驱动/制动控制切换策略Simulink仿真过程示意图
3.4 底层控制器设计
根据切换策略判定,当自车驱动时,以车辆安全性为首要目标,具有基于模糊控制的驱动控制器。在自车制动时,根据纵向动力学模型对被控车辆进行制动。
3.4.1 基于模糊控制的驱动控制器设计
将二维模糊控制器作为驱动控制器,其中输入量为加速度误差及误差变化,输出量为车辆需要的期望转矩。定义加速度误差、加速误差变化和期望转矩的语言变量转化为7个模糊集合,语言变量值分别为

其中,NB为负小,NM为负中,NB为负大,ZO为零,PS为正小,PM为正中,PB为正大。
在车辆行驶过程中,需要自车有较好的响应速度,故设计的模糊控制器输入和输出变量选用三角形隶属度函数(Trimf)。经过对模糊规则反复调试和验证,建立了底层驱动模糊控制规则(见表3),共49条规则。

表3 驱动模糊控制规则
通过建立的模糊控制规则,采用Matlab内的三维图分析输入与输出之间的关系,如图4所示。2个输入变量化的模糊论域范围为[-5.5 3.5]和[-1 1],输出变量的模糊论域范围为[0 20]。

图4 模糊控制输入变量和输出变量三维图
采用Mamdani推理,Simulink仿真模型如图5所示。

图5 模糊驱动控制器仿真模型示意图
3.4.2 基于纵向动力学模型的制动控制
制动控制过程中,由期望减速度求得制动主缸的期望制动压力,将期望制动压力作用在车轮上,控制车辆减速行驶。
根据车辆动力学分析可知,在良好的水平道路上匀速行驶时,受到的行驶阻力为:

式中:Ff为滚动阻力;Fw为空气阻力。
可由式(22)表示:

在制动过程中,当车轮的附着率小于等于地面附着系数时,期望制动压力可以由式(23)表示:

式中,pdes为期望制动压力。
求得期望制动压力为:

纵向制动控制Simulink仿真模型,如图6所示。

图6 纵向制动力矩Simulink仿真模型示意图
4 仿真验证
基于Carsim/Simulink联合仿真平台,对不同工况进行仿真,验证了安全距离模型以及分层式控制器对车距控制的有效性和鲁棒性。
4.1 Carsim/Simulink联合仿真模型
将Carsim软件的外部接口与Simulink中的控制模型进行联合,车辆动力学模型的输入变量为驱动力矩与制动主缸力矩,输出变量为自车速度、加速度以及两车相对速度与距离。模型输出作为顶层控制器的输入,进而得到车辆的期望加速度,将其作为底层控制器的输入,实现对车辆的控制。联合仿真模型如图7所示。

图7 Carsim/Simulink联合仿真模型示意图
4.2 跟车起停仿真分析
仿真环境为附着系数0.85的良好路面,自车与前车的初始距离为8 m。仿真结果如图8、9所示。

图8 自车速度与前车速度

图9 期望距离与实际距离
实验过程中,自车速度由静止加速到9 km/h,经过3 s与前车速度持平,自车车速与前车速度变化趋势基本保持一致,两车停止时,自车停止在距前车2 m的安全位置。因此,对于跟车起-停工况,速度响应较快,能够保持安全行驶距离,控制器有较好的效果和鲁棒性。
4.3 定速巡航仿真分析
定速巡航是指车辆按照设定速度稳定行驶,主要分为加速、减速2种巡航模式。
1)低速变高速巡航
车辆起始初速度为40 km/h,设定80、100、110 km/h 3种期望速度,仿真结果如图10、11所示。

图10 期望车速和实际车速
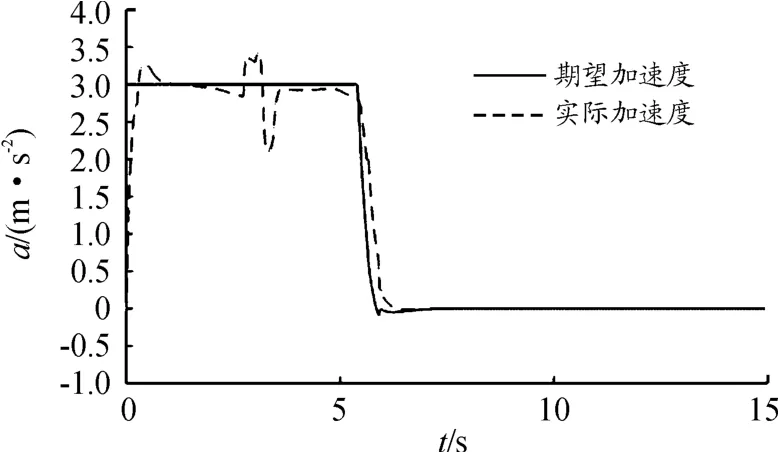
图11 100 km/h时加速度
仿真开始时,自车以40 km/h的初速度加速行驶,在4、6、7 s时达到不同的期望车速,并稳定行驶至结束,实际加速度和期望加速度变化趋势基本一致。因此,控制器对低速变高速巡航有较好的控制效果和鲁棒性。
2)高速变低速巡航
车辆初始速度为110 km/h,设定期望速度为70、50、30 km/h。仿真结果如图12、13所示。
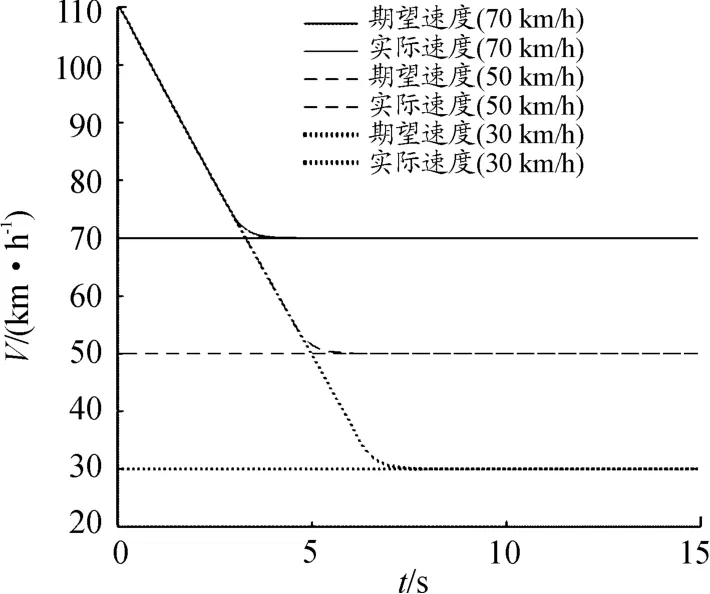
图12 期望车速和实际车速

图13 50 km/h期望加速度和实际加速度
仿真开始时,自车以110 km/h的初速度按照期望速度减速行驶,在3、5、7 s时达到不同的期望速度,并稳定行驶至结束,实际加速度和期望加速度变化趋势基本一致。综上所述,控制器对低速变高速巡航同样有较好的控制效果和鲁棒性。
4.4 距离保持仿真分析
距离保持工况是指自车与前车保持一定安全距离,跟随前车行驶。距离控制的前提是目标车辆车速低于车辆的巡航速度。根据车速不同分成低速跟踪工况和高速跟踪工况。
1)低速跟驰
低速跟踪工况适用于城市工况行驶,仿真起始两车实际距离20 m,自车初始速度15 km/h,前车初始速度10 km/h,进行2次加速、减速之后,稳定在20 km/h。
仿真结果如图14、15所示,自车速度与前车速度变化趋势一致,两车的实际距离在期望距离附近波动,波动误差小于0.3 m,控制器能够在保持距离的前提下,控制车辆安全稳定地跟随前车,满足低速跟踪工况的需求。

图14 前车速度和实际速度

图15 期望距离与实际距离
2)高速跟驰
高速跟踪工况适用于车流量较少的高速工况,仿真起始两车实际距离为40 m,自车初始速度为70 km/h,前车初始速度为60 km/h,进行2次加速、减速,稳定在70 km/h。
仿真结果如图16、17所示,自车速度与前车变化趋势一致,两车的实际距离始终在期望距离附近波动。表明,控制器具有较好的控制效果和鲁棒性,满足高速跟踪工况的需求。
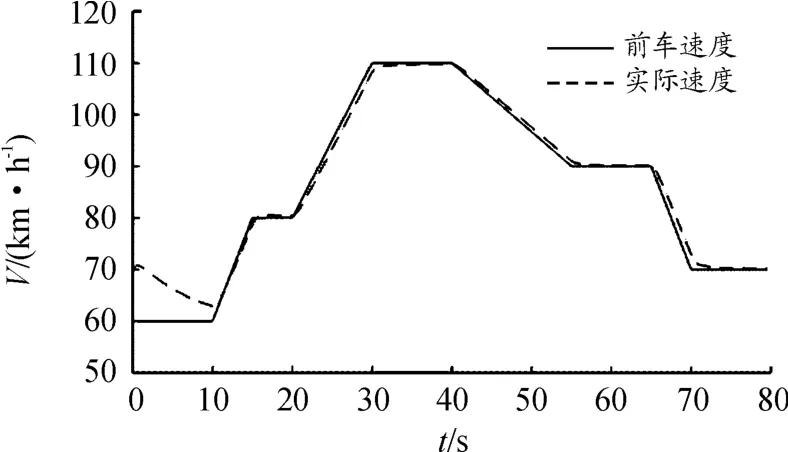
图16 前车速度和实际速度
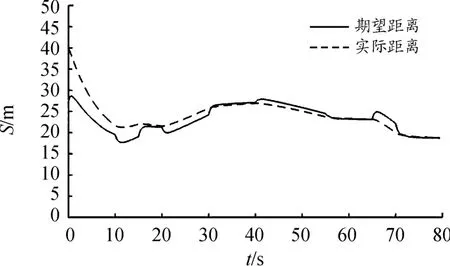
图17 期望距离与实际距离
5 结论
1)基于Carsim/Simulink平台,对驱动电机模型进行选取,并建立纯电动汽车动力学模型。
2)对典型的安全距离模型进行改进,提出了一种考虑极端条件和制动器起作用时间的可变安全距离模型。
3)采用分层式控制结构对控制器进行设计,设计了以LQR控制理论为基础的车距保持顶层控制器,基于PID控制的车辆巡航顶层控制器。通过建立的驱动/制动切换策略,将期望加速度传递给基于模糊理论的底层控制器或基于动力学数学模型的制动控制。
4)针对起、停工况定速,巡航工况和距离保持工况进行车距控制的仿真验证。结果表明:搭建的安全距离模型和分层式控制器具有较好的控制效果和鲁棒性,使车辆能够安全稳定行驶。

