公路工程重荷箱涵的扣件式模板支撑体系验算与数值分析

■林中群

（福建省交建集团工程有限公司， 厦门 361021）

在公路工程中不可避免会出现超高、 重荷、大跨的结构，如大型的公路桥、公路通道箱涵、公路隧道等，具有建设高度高、自重大、跨度长的特点。 这些超高、重荷、大跨结构在施工过程中都需要用到模板支撑体系作为临时结构， 以完成结构的浇筑、养护。 所以，模板支撑是超高、重荷、大跨工程顺利施工的重要保障。

由于结构具有超高、重荷、大跨的特点，使得模板支撑面临的各种难题，如受力形式复杂、搭设难度大、现场管理要求高等，也使得模板支撑成为施工工程的重大危险源之一。 扣件式模板支撑是我国工程施工中最常用到的形式，一般通过扣件的机械连接完成整个支撑体系的搭建， 具有施工便捷、灵活拆卸的优点，常用于各种超高、重荷、大跨的建设工程。 尽管国家已通过多项技术规范[1-2]保障扣件式模板支撑安全施工，但由扣件式模板支撑引起的工程事故仍然频发。 如某污水池项目属于高大模板支撑体系，但存在扣件式支撑设置间距过大，未设置水平剪刀撑，方案设计不合理等问题，在浇筑时发生倒塌事故[3]。 漳州某度假区的桥梁梁板属于重荷结构，在混凝土浇筑中也发生了扣件式支撑坍塌事故，同样存在模板支撑设计方案不合理现象[4]。 因此，针对超高、重荷、大跨结构下扣件式模板支撑体系的合理设计、计算对保障工程安全施工具有重大意义。

以福建省南靖县的某段公路工程通道箱涵为例，由于施工总荷载均超过规定数值，属于重荷结构，因此，模板支撑体系是施工过程中的重大危险源之一，需要对其安全性进行专项分析验证。 本研究结合相关规范，设计了扣件式模板支撑体系的实施方案，并验算其受力、变形和稳定性。 最后，结合有限元分析方法， 进一步验算实施方案的可行性，验证了其准确性和有效性。

1 工程概况

1.1 通道箱涵设计

通道箱涵上跨县道， 县道为一级设计等级公路。 通道箱涵的净高为5.3 m，通道长度为58.0 m，净宽度为8.0 m，顶板厚度为0.7 m，结构类型为钢筋混凝土箱形断面（图1）。

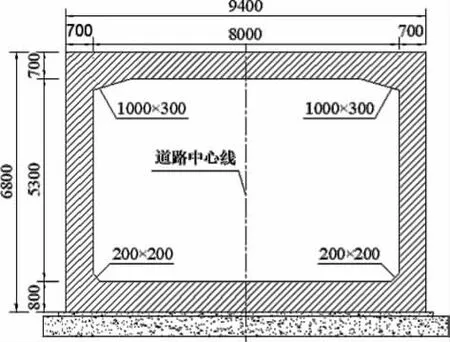
图1 通道箱涵断面

1.2 超高重荷大跨结构的判定

相关规范规定[5]模板支撑：架立高度H>8 m，平面跨度L>18 m， 支撑上部的施工阶段荷载总和>15 kN/m2，集中线荷载>20 kN/m，属于超高、重荷、大跨结构。

本研究通道箱涵的施工总荷载依据规范规定[1]，计算如下：

其中， 荷载组合效应系数： 永久荷载系数取1.3，可变荷载系数取1.5；S－施工总荷载的组合设计值；G1k－模板自重荷载， 取0.3 kN/m2；G2k－混凝土自重 荷 载， 取24 kN/m3；G3k－钢 筋 自 重 荷 载，取1.1 kN/m3；T－混凝土结构板厚， 取0.7 m；Qlive－操作员及操作设备的面荷载，取2.5 kN/m2。通过公式（1）计算可得，施工总荷载为26.981 kN/m2，大于规定的15 kN/m2， 而高度5.3 m 和宽度8.0 m 均小于规定值，因此本研究的通道箱涵可判定为重荷结构。

1.3 施工材料要求

支撑立杆和水平杆采用Φ48.3×3.6 mm 的圆钢管，钢管强度为205.0 N/mm2。 模板采用厚度15 mm的胶合板， 主楞选用截面为50×50 mm、 厚度为3 mm 的双方钢管， 次楞选用截面为50×90 mm 方木。 力学参数如表1 所示。

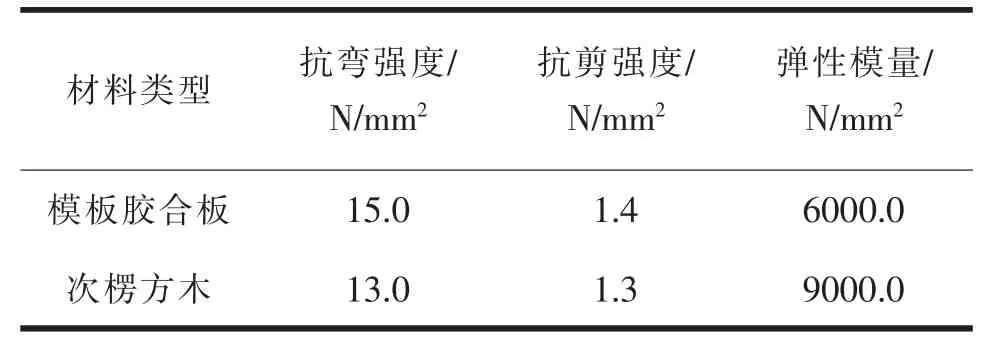
表1 材料的力学参数

1.4 模板支撑搭设方案

支架立杆纵距la、横距lb设为600 mm，步距lh为1 200 mm，支架坐落在箱涵底板上，立杆底部铺垫不短于三跨的50 mm×2 000 mm 的垫板。 板底次楞方木布设间距l 取200 mm。 剪刀撑每隔4 排立杆、 两步距高度设置。 扫地杆设在距地面200 mm处。 顶托为可调高度形式， 但伸出螺杆不超过200 mm。 模板支撑具体搭设见图2。

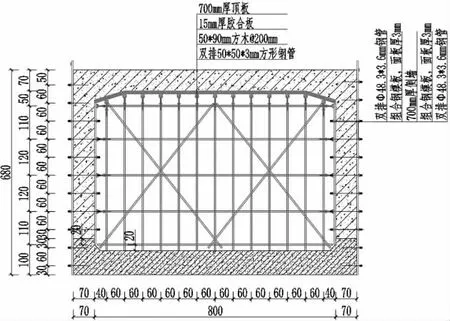
图2 模板支撑的搭设

2 模板支撑设计验算

2.1 模板面板验算

2.1.1 荷载计算参数

模板面板是水平构件， 以承受弯矩作用为主，因此，验算其在重荷作用下的截面弯曲强度和变形情况是否符合规范要求。 计算模型取1.0 m 面板为研究对象，并将其简化为三跨连续梁，荷载计算参数为：（1）自重：模板取0.30 kN/m2，钢筋取1.1 kN/m3，混凝土取24 kN/m3。（2）活载：均布荷载取2.50 kN/m2，另外，以集中荷载2.5 kN 进行验算。 静荷载标准值q1=Gdead×1 m=17.87 kN/m，活荷载标准值q2=Qlive×1 m=2.5 kN/m。 （3）截面惯性矩I=bh3/12=（1 000×153）/12=281 300 mm4，截面抵抗矩W=bh2/6=（1 000×152）/6=37 500 mm3。

2.1.2 抗弯强度验算

依据三跨连续梁的最不利弯矩分布，对三个部位的最大弯矩值进行计算，包括：均布荷载的最大弯矩M1，均布荷载与集中荷载组合荷载下的支座弯矩M2及跨中最大弯矩M3进行计算， 并取最大值Mmax=Max[M1，M2，M3]，其中：

（1）M1=0.100×（1.30×17.870+1.50×2.500×0.200×0.200=0.108 kN·m；

（2）M2=0.100×1.3×17.87×0.20×0.20+0.100×1.5×2.5×0.20=0.168 kN·m；

（3）M3=0.080×1.3×17.87×0.25×0.25+0.200×1.5×2.5×0.25=0.224 kN·m。

将计算得到的弯矩Mmax=0.224 kN·m，结构重要性系数γ0=1.0，截面抵抗矩W=37 500 mm3，代入到公式（3）：

可得，面板的抗弯强度f=5.97 N/mm2＜[f]=15.0 N/mm2，满足要求。

2.1.3 挠度验算

已知q1=17.87 kN/m，方木间距l=200 mm，弹性模量E=6000 N/mm2， 惯性矩I=281 300 mm4，代入到公式（4）：

可得，v=0.115 mm＜[v]=0.5 mm，满足要求。

2.2 支撑立杆验算

由于支撑立杆搭设高度较低，受风荷载影响较小；同时，由于通道箱涵的特点是通道长度远大于其宽度，而受风方向为通道长度方向，支撑立杆采用满堂架布设方式，在受风方向布设数量远大于非受风方向，可得风荷载对其稳定性的影响可以忽略不计。

2.2.1 计算参数

2.2.2 立杆稳定性验算

不考虑风荷载时，立杆的稳定性公式为

其中，γ0－重要性系数， 已知为1.0；N－立杆轴力，取9.713 kN；φ－压杆稳定系数，根据规范[1]计算长度l0=1.155×1.546×（1.2+2×0.2）=2 857 mm， 回转半径i=15.9 mm，因此l0/i=179.68，查表得φ=0.243；A－钢管横截面面积，为4.24 mm2；σ－钢管抗压强度计算值；f－钢管抗压强度设计值，取205.00 N/mm2。

将以上系数代入公式（5）计算得，σ=94.25 N/mm2＜f=205 N/mm2，满足要求。

2.2.3 整体稳定性验算

依据规范GB51210-2016《建筑施工脚手架安全技术统一标准》中（6.2.15-1～6.2.15-17），模板支撑体系应考虑整体抗侧向稳定性。 验算应符合规范要求：

其中，MOk－侧向弯矩设计值；MR－抗侧向弯矩设计值。

（a）抗倾覆力矩MR的计算

其中，B－支撑体系的布设宽度（图2），取8.0 m；la－立杆与立杆之间的纵向距离，取0.6 m；g1k－支撑自重面荷载标准值， 已知横向间距lb=la=0.6 m，N1=0.734 kN，因此，g1k=N1/（la×lb）=2.038 kN/m2；g2k－模板自重面荷载，取0.30 kN/m2。

[46]《明英宗实录》（台北1962年影印本）卷二二四，《明史》，北京：中华书局，1974年，卷一六二，倪敬传。

将以上参数代入公式 （7） 可得， 抗侧向弯矩MR=8.002×0.600×（2.038+0.300）=89.78 kN·m。

（b）侧向弯矩MOk的计算

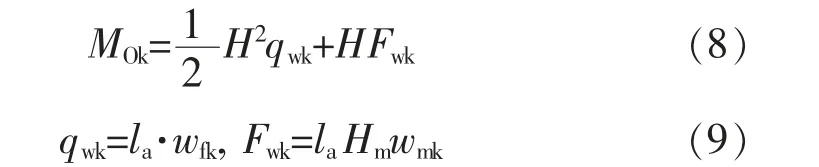
其中，H－支撑高度， 取5.3 m；wfk－风荷载标准值，根据GB51210-2016《建筑施工脚手架安全技术统一标准》 中的式 （5.1.7） 可得，wfk=1.09×1.00×0.500=0.545 kN/m2；Hm－支撑顶部防护栏杆的高度，取0.4 m；wmk－模板或支撑受风载作用形成的水平力，与wfk一致，取0.545 kN/m2。 qwk－风作用的线荷载标准值，qwk=0.6×0.545=0.327 kN/m；Fwk－风荷载作用在模板支撑体系上的水平力标准值，Fwk=0.6×0.4×0.545=0.817 5 kN。

通过公式 （8）、（9） 可计算得，MOk=0.5×5.32×0.327+5.3×0.8175=8.925 kN·m。

（c）验算

综上， 通过计算得到的MOk=2.191 kN·m，MR=89.78 kN·m，代入到公式（6）可得：3γ0MOk=3×1.0×8.925=26.775 kN·m＜MR=89.78 kN·m，因此，支撑的整体稳定性满足要求。

3 模板支撑的有限元分析

3.1 有限元建模

通过Abaqus 有限元软件， 对模板支撑在施工荷载下的应力情况进行仿真分析。 模板的长取为8 m，宽为8 m，厚度为0.015 m，弹模为12 000 MPa，泊松比为0.1，抗压强度为40 MPa。 支撑的横距为0.6 m，纵距为0.6 m，步距为1.2 m，钢管直径为48 mm，壁厚为3 mm，弹性模量取206 000 MPa，泊松比为0.3。钢管的屈服强度为205 MPa，抗拉强度为375 MPa。

立杆、 水平杆和剪刀撑都是采用钢管布设，受到弯矩、剪力和轴力作用，因此采用B32 梁单元模拟；模板的厚度远小于长度和宽度，因此采用S4R壳单元模拟。 采用扣件连接节点的刚度通过线性弹簧模拟，竖直方向弹簧刚度取20（kN·m）/rad 的半刚性连接，以模拟扣件的摩擦滑移，其他方向的弹簧刚度设为无穷大。 立杆底部与基础的边界连接采用铰接；水平杆的两端是紧靠墙壁设置，因此设为单链杆铰接形式。 通过前述的施工总荷载为26.981 kN/m2可得， 支撑在8 m×8 m 的浇筑面积下施工总荷载为Ntotal=1 726.784 kN。 当荷载加至Ntotal 时，立杆钢管的应力小于屈服强度205 MPa，也说明了设计方案是可靠的。

3.2 特征值屈曲分析

利用特征值屈曲分析获得模板支撑可能潜在的失效模式，通过各个模态可以了解本研究的模板支撑体系在竖向荷载下的变形，及各个模态下结构体系的特征承载力。 计算模板支撑体系的前三阶模态见图3。

图3 模板支撑体系的模态分析

从图3 可知，体系的一阶模态呈波浪形状，且形成反对称形式，这与相关的模板支撑体系静力试验变形模式测量结果相吻合[6]，说明了有限元建模的可靠性。 一阶模态对应的特征值承载力为26 396.6 kN，为施工总荷载的15 倍， 说明模板支撑的布设形式具有良好的承载能力。 由于特征值承载力是理想状态下模板支撑的承载力，但实际情况下，支撑可能存在初始缺陷，削弱了结构的力学性能，因此，需要进一步对结构进行非线性静力分析。

3.3 非线性静力分析

通过前述的屈曲分析发现一阶模态的失效模式符合模板支撑的实际变形情况，因此取一阶模态的失效模式，通过引入模态比例因子lh/1000（lh为步距）以模拟结构存在的初始缺陷。 钢材采用二折线模型，强化阶段斜率取弹性模量的1%。 最后，将分析步骤的非线性开关打开，实现体系的非线性静力分析。 图4 为结构在施工总荷载及达到钢管屈服强度时的应力云图。

图4 支撑体系的应力云图

从图4（a）可知：（1）当荷载加至施工总荷载1 726.8 kN 时，支撑的Mises 应力最大为55.96 MPa，相当于钢管屈服强度的1/4 左右， 支撑立杆明显处于弹性阶段， 说明了现有的支撑体系可以满足施工过程中的受力需求；（2）当支撑体系的应力达到钢管的屈服强度205 MPa 时，对应的荷载为6 371.89 kN，为施工总荷载的3.7 倍， 此时对应的竖向位移为2.17 mm。 说明模板支撑体系具有较大的冗余度，不仅可保证结构的安全施工，同时，产生的竖向位移沉降较小，不会影响结构的施工质量；（3）模板支撑体系的极限承载力为19 835.3 kN，为施工总荷载的11 倍，可以有效满足结构施工的需求，验证了所提出的体系设计方法可行性。

4 结论

本研究结合相关规范要求，对模板支撑体系中模板在弯矩作用下的强度和变形，以及支撑的抗侧向能力进行了验算，并结合有限元分析，进一步验证了模板支撑体系设计方法的准确性。 得到以下结论：（1）方木的间距和截面尺寸选取显著影响模板面板的抗弯强度和挠度验算，因此选取方木的尺寸和间距应严格按照规范要求；通过对支撑的立杆稳定性和抗倾覆能力进行验算，证明了所采用的布设方法和立杆尺寸满足结构施工要求；（2）通过有限元分析得出了模板支撑体系在达到施工总荷载时，钢管处于弹性阶段。 且钢管达到屈服强度时，体系的荷载达到施工总荷载的3.7 倍， 证实了现有的模板支撑体系施工方案具有一定的冗余度，完全满足施工安全和工程质量的要求；（3）南靖县靖城棋盘社至牛崎头段公路工程，目前所涉及通道涵等构造物已全部完成并交工验收合格， 本项目参与2020年度信用考核A 级，也证实了设计方案的可靠性。