驾驶人“感知-决策-操控”行为模型

冯树民，黄秋菊，张宇，赵琥

(1.哈尔滨工业大学，交通科学与工程学院，哈尔滨150010；2.哈尔滨职业技术学院，汽车学院，哈尔滨150081)

0 引言

近年来对于汽车主要操控者行为的描述、理解和深入研究已成为国内外学者关注的重点[1]。已有研究表明，应用数学模型对驾驶人的驾驶操控行为过程进行准确模拟和刻画，并体现该过程中驾驶人的经验和自身特征，是研发更先进的智能化驾驶辅助系统和自动驾驶技术，推动智能网联交通发展的重要手段之一[2]。1981年，REDDY等[3]开始驾驶人行为建模研究，并提出一种驾驶人行为模型。经过近40年的发展，对驾驶人行为的建模主要归纳为4种方法：基于传递函数的驾驶人行为建模[4]，基于最优控制的驾驶人行为建模[5]，基于数据的驾驶人行为建模[6]，基于模型预测控制的驾驶人行为建模[7]。

已有研究更多是从方向盘转角、预瞄路径等建立描述驾驶行为的模型，缺少对驾驶行为过程随机性和动态性的考虑。为此，本文采用随机模型预测控制方法，基于HMM 提出驾驶人“感知-决策-操控”行为模型，使模型预测更符合真实驾驶状态。另外，已有研究大多采用间接计算获得的车头时距等确定模型参数，本文利用直接观测的自然驾驶数据，实现对模型有效性和准确性的验证。

1 马尔可夫理论与驾驶行为的关系

1.1 隐马尔可夫模型

隐马尔可夫模型(Hidden Markov Model，HMM)是马尔可夫理论模型中常见的一种，通常用模型中可观测的参数计算并确定模型中未知和不容易观测的参数。如图1所示。

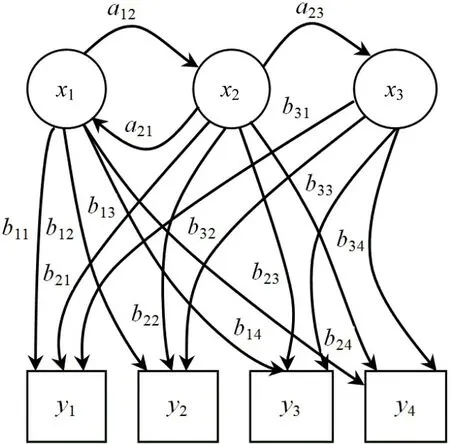
图1 隐马尔可夫模型图示Fig.1 Diagram of hidden Markov model

图1中，状态xi为HMM 中不容易直接观测到的隐含状态，但可以通过可观测的输出状态yj确定，这些状态之间满足马尔可夫性质；aij表示隐含状态之间的转移概率；bij表示隐含状态与输出状态之间的转移概率。

1.2 HMM与驾驶行为关系分析

驾驶人的感知过程通常是不确定的、动态的，且随时间变化，说明驾驶人决策过程和操纵过程具有随机性。因此，用服从马尔可夫链的随机过程来描绘驾驶行为是科学有效的。虽然，驾驶员的感知过程、决策过程和操纵过程是不容易观测的隐含状态，但是可以通过可观测的输出信息，例如车头时距或车间时距等体现。如果通过计算间接获得输出信息，会影响模型的准确性和精度。本文以车间距作为HMM中的可观测输出，采用雷达测距传感器测量实时车间距，保证可观测输出层的准确性，提高模型预测的准确性。利用隐马尔可夫理论，以最常见的跟车行驶为例，对驾驶人驾驶操控行为建模。前后两车车间距离示意如图2所示。

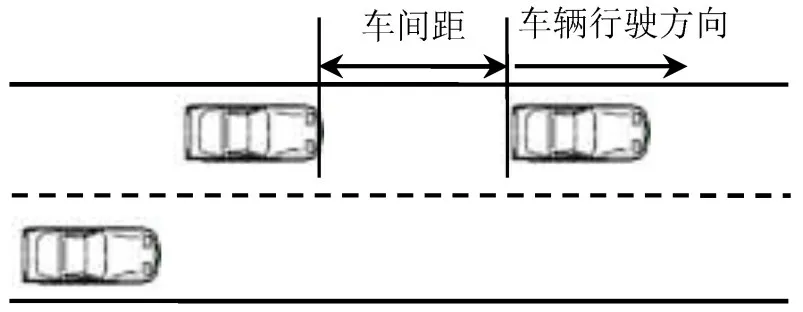
图2 前后两车车间距离示意Fig.2 Schematic diagram of workshop distance between front and rear cars

2 驾驶人“感知-决策-操控”行为模型设计

2.1 模型框架设计

驾驶人“感知-决策-操控”行为模型框架如图3所示。

图3 驾驶人“感知-决策-操控”行为模型框架Fig.3 Driver perception-decision-manipulation behavior model framework

如图3所示，在基于HMM 的驾驶人“感知-决策-操控”行为建模框架中，基于HMM的驾驶人驾驶意愿模型模拟驾驶人感知过程，即获得期望的车间距；预测模块模拟驾驶人根据交通环境和自身生理、心理状态预测未来车辆行驶路径，即决策过程；优化模块模拟驾驶人为实现预测车间距对期望车间距的追踪，而采取的措施和动作，即操控车辆加速、减速等。3 个模块的滚动优化过程实现对驾驶人跟车行为的模拟和描绘。

2.2 基于HMM的驾驶意愿建模

2.2.1 驾驶人驾驶意愿的数学描述

车辆行驶过程中，驾驶人根据感知到的信息产生驾驶意愿操纵车辆运行，车速是驾驶意愿的主要直观体现，因此，可以用每秒钟的速度变化量ΔV(ΔV ＞0,ΔV ＜0,ΔV=0)来描述驾驶人的驾驶意愿，即加速、减速或匀速。假设车辆行驶过程中纵向速度变化所在区间为[ΔVmin,ΔVmax] ，将其平均分割成NX份，其中，ΔVmin和ΔVmax分别表示速度变化量最小值和最大值，X等于HMM中隐含状态的个数。

2.2.2 驾驶人驾驶意愿模型构建

如图3所示，在驾驶过程中，驾驶人的驾驶意愿具有较强的随机性。因此，按照随机过程的定义，驾驶人的驾驶意愿可以用随机过程{Xt,t∈[ 0 ,+∞)}来描述。假设其概率分布列Π=(pi)为

式中：pi表示随机状态的概率，p1+p2+…+pNX=1。于是，驾驶意愿即随机过程{Xt,t∈[ 0 ,+∞)}具有马尔可夫性质。用概率转移矩阵A表示驾驶意愿各状态之间的转移概率为

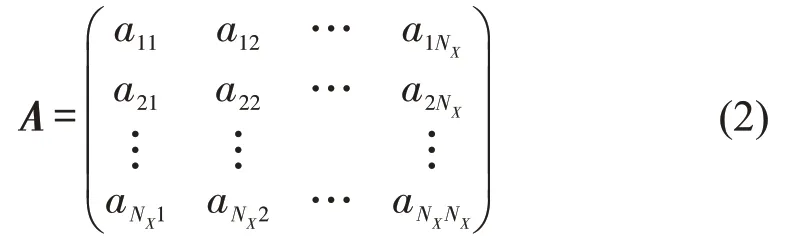
式中：aij=P(Xt+1=j|Xt=i),1 ≤i,j≤NX表示t时 刻ΔV位于第i个区间[ ΔVxi-1,ΔVxi)，而在t+1 时刻ΔV位于第j个区间[ ΔVxj-1,ΔVxj)的概率为aij。

在驾驶操控行为过程中，驾驶意愿即HMM 中的隐含状态可由两车的车间距离来体现。试验中借助雷达模块实时测量与前车的车间距。将车间距所在的区间[Smin,Smax] 分割为NY个子区间，这里Smin、Smax分别表示车间距最小值和最大值，NY个子区间数目即为HMM 中可观测的输出状态数目。当m时刻期望的车间距Sm位于第i个子区间[Smi-1,Smi)时，即表示对应的输出状态为Y=i。

根据图3分析可知，驾驶操控行为的可观测输出状态，即车间距的取值主要取决于驾驶人多通道感知信息后产生的驾驶意愿，因此，可以用条件概率bij=P(Yt=j|Xt=i),1 ≤i,j≤NY表示两者之间的关系。该条件概率bij表示当HMM的隐含状态，即驾驶人的驾驶意愿位于第i个子区间[ΔVxi-1,ΔVxi)时，可观测输出状态，即车间距位于第j个子区间[Smj-1,Smj)的概率为bij。可观测输出状态概率转移矩阵B为

于是，利用隐马尔可夫模型λ=(A,B,Π)实现图3中驾驶人感知过程的模拟，即驾驶意愿模型为

式中：Xk为HMM 中的隐含状态，即车辆每秒纵向速度变化量ΔV；Yk为可观测的输出状态，即车间距S；k表示时刻。

3 驾驶人“感知-决策-操控”行为建模

在驾驶操纵过程中，驾驶人基于自身当时的生理、心理状态及驾驶经验和习惯，通过视觉、听觉、触觉、空间运动感知等综合感知车内外的状态，将多通道获得的多源信息进行融合处理，获得期望的车间距序列[Smj(k+1),Smj(k+2),…,Smj(k+Np)]，其中，Np为驾驶人感知的安全车间距的状态数，p表示个数。同时，驾驶员根据当前车辆状态，在不与他车驾驶意愿冲突的条件下，对下一时刻车辆状态进行预测。根据式(2)和车辆当前状态，可以得到预测输出序列为

式中：Ypk+i=BAiXk,i=1,2,…,Np。

驾驶人通过对车辆的操控，实现预测车间距对期望车间距的跟踪，即获得隐含状态序列。在已建立的隐马尔可夫模型λ=()A,B,Π情况下，借助MATLAB 采用维特比算法(Viterbi algorithm)实现驾驶人驾驶意愿序列的产生，即完成预测车间距对期望车间距的跟踪。因此，驾驶人“感知-决策-操纵”行为模型为

式中：X(k)为待优化的驾驶人意愿序列，即车辆的控制输入序列，X(k)=(Xk+1,Xk+2,…,Xk+Np)T；Yd(k)为期望的输出序列。 为实现优化，Yd(k)=(Ydk+1,Ydk+2,…,Ydk+Np)T。根据贝叶斯公式

在输出序列Yd(k)已知情况下，条件概率P[X(k)|Yd(k)]的取值与P[Yd(k)]的取值无关。因此，条件概率P[X(k)|Yd(k)]的最大值，即如下函数的最大值。

具体优化过程如下：

当Np=1时，

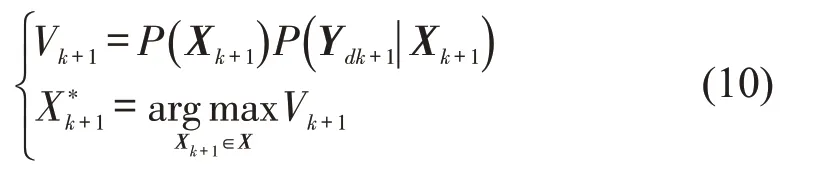
当Np=2 时，

以此类推，当Np=Np时，

因此，

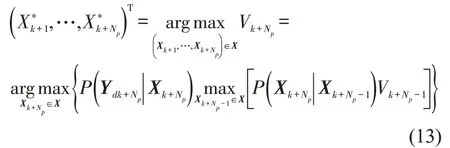
将上述递推过程归纳为：

Step 1 将控制时域Np输入，并输入状态概率分布列Π，隐含状态概率转移矩阵A和可观测输出概率转移矩阵B。

Step 2 输入期望的观测序列Yd(k)=(Ydk+1,Ydk+2,…,Ydk+Np)T。

Step 3 初始化Vk=0。

Step 4 根据迭代公式Vk+i=P(Ydk+i|Xk+i)P(Xk+i|Xk+i-1)Vk+i-1,i=1,2,…,Np，计算待优化函数值。

Step 5 计算控制输入序列X(k)。

Step 6 将X(k)的第一个元素作用于系统。

Step 7 在k+1 时，有可观测序列Yd(k+1)，令k=k+1，回到Step 2。

MATLAB 中具有实现维特比计算方法的求解功能，故借助MATLAB完成计算。

4 模型参数辨识和应用示例

4.1 自然驾驶数据调查与处理

数据为项目研究人员于2019年5月-12月在哈尔滨市城市道路所收集的共5591 km、6840 min的自然驾驶数据。其中，2019年12月16日-23日，分别于早6:35-7:35，晚16:00-17:00，通过雷达测距，传感器以0.1 s为步长记录10台不同试验车辆与前车的车间距，并借助手机APP同步测量并记录试验车辆的运行数据，包括：实时速度，纵向位移，最高速度，累计行驶公里数等信息。采用对称指数平均滤波算法对16 段时间所记录的数据进行选取，得到2178457+1853781=4032238组数据。

4.2 模型参数辨识

为获得模拟驾驶人“感知-决策-操控”行为过程的HMM模型，需要辨识模型中状态概率分布列Π，状态概率转移矩阵A和输出概率转移矩阵B。对滤波后的车间距数据计算并统计。车间距小于1.5 m 和大于16.5 m 的数据量较少，仅占数据量的11.13%，不作为重点研究内容。为更好地体现数据的统计规律性，具体刻画和描绘驾驶人不同交通流状态下驾驶操控行为，按照车间距间隔6 m进行分类，获得[1 .5,7.5)m，[ 7.5,13.5)m，[1 3.5,19.5)m 这3 个车间距区间，各自对应数据量如表1所示。

表1 按照车间距划分后的统计数据Table 1 Statistical data table by vehicle spacing

为获得HMM 模型中隐含状态的概率分布列，即ΔV的概率分布列，先将车辆速度变化所在区间[ΔVmin,ΔVmax]划分为NX个子区间，依据大样本量情况下频率近似概率思想，获得车辆速度变化量位于每个区间的概率，即

式中：nΠi为车辆的速度变化量位于区间[ ΔVxi-1,ΔVxi)的样本点的数量；nΠ为研究区间(车间距区间)内样本点的总数；pi为车速变化量位于[ ΔVxi-1,ΔVxi)区间的频率。取NX分别为8、10 和8，计算获得车间距[1 .5,7.5)m ，[ 7 .5,13.5)m ，[1 3.5,19.5)m 这3 个区间上，车辆速度变化量的概率分布列，如表2所示。

表2 车辆速度变化量概率分布列ΠTable 2 Probability distribution of vehicle speed variation Π

同理，分别将车辆速度变化量区间[ΔVmin,ΔVmax]划分为NX个子区间，将输出车间距变化区间[Smin,Smax] 划分为NY个子区间。采用大样本量下频率近似概率的方法，通过式(15)和式(16)计算获得车辆速度变化的概率转移矩阵A=[aij]及输出概率转移矩阵B=[bij]。

式中：nAij为车辆的速度变化量位于区间[ ΔVxi-1,ΔVxi)的样本点的数量；nAi为研究区间内样本点的总数；nBij为车辆的速度变化量位于区间[ ΔVxi-1,ΔVxi)，车间距位于区间[Smj-1,Smj)的样本点的数量；nBi为研究区间内样本点的总数。

取不同的NX和NY，计算获得车间距[1 .5,7.5)m，[ 7 .5,13.5)m，[1 3.5,19.5)m 这3 个区间上车辆速度变化的概率转移矩阵A=[aij]及输出概率转移矩阵B=[bij] 。以车间距[1 .5,7.5)m 为例，结果如表3和表4所示。

通过计算结果可以看出，表3和表4中的行最大值有7/10 位于对角线上；同理，发现另外两个车间距区间下概率转移矩阵计算表中的行最大值分别有8/10 和7/10 位于对角线上。这表明车辆速度变化量在下一时刻有73.3%向自身所在的区间转移，即速度变化呈现平稳状态。通过计算还可以看出，每行的次最大值有82.14%向自身所在区间的相邻区间进行转移。说明驾驶人在短时间内倾向于操控车辆平稳运行，没有急加速或急减速的驾驶决策和行为。这与大多数驾驶人的驾驶操控行为特性相吻合。说明模型可以实现对驾驶人“感知-决策-操控”行为过程的模拟和预测。

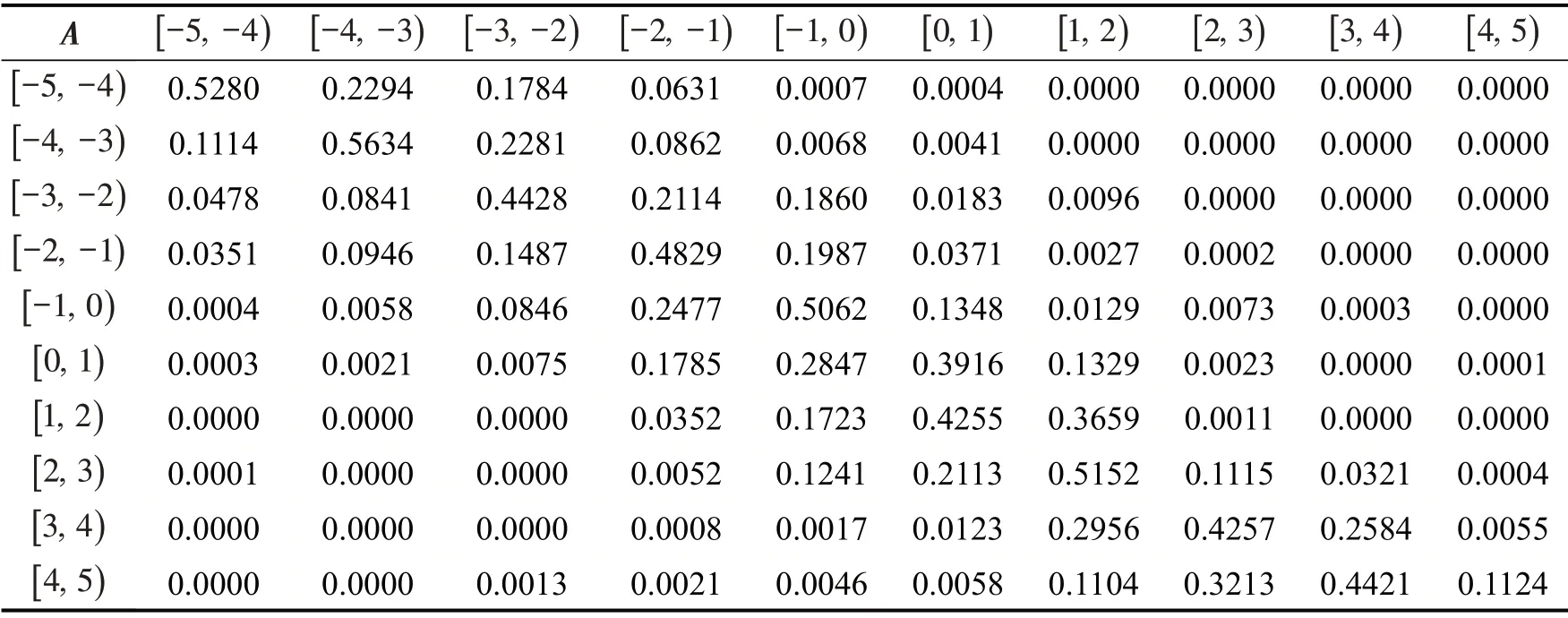
表3 车速变化量概率转移矩阵ATable 3 Probability transfer matrix A of vehicle speed variation

表4 输出车间距概率转移矩阵BTable 4 Probability transfer matrix B of output vehicle spacing

4.3 应用示例

重新选取编号为006号、008号和019号的3辆车作为研究算例，分别采集3辆车15 min的自然驾驶数据，如表5所示。

表5 隐含状态车辆速度变化量区间划分Table 5 Interval division of vehicle speed variation in hidden state

通过辨识获得Π、A和B，使用MATLAB 中HMM 工具箱中的命令multinomial-prob 和viterbipath实现维特比优化方法，得到待优化的驾驶人决策序列，如表6所示。

表6 输出状态车间距区间划分Table 6 Interval division of output state

根据优化算法得到3辆车的闭环响应曲线，如图4～图6所示。可以看出：模型仿真与实际车间距的总体趋势一致，整体近似效果较好；比较实际车间距和模型仿真后获得车间距，模型预测的车间距平均误差仅为1.47%；样本量越大，隐含状态和输出状态区间划分越细致，仿真效果与实际数据一致性越好，模型的预测准确性越高。表明：所建立的基于HMM驾驶人“感知-决策-操控”行为模型，克服了传统模型应用时对交通场景的限定及缺乏对驾驶行为过程随机性和动态性考虑的问题，可以更好地模拟和描述驾驶人跟车驾驶行为。

图5 编号008车辆的模型仿真与实际车间距对比图Fig.5 Comparison between model simulation and actual vehicle spacing of vehicle No.008

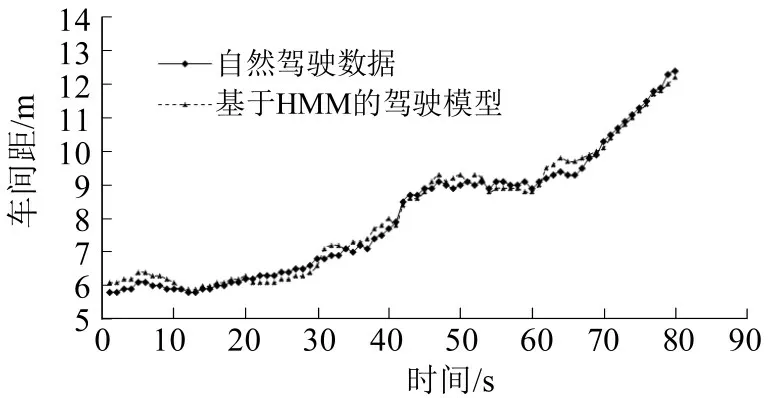
图6 编号019车辆的模型仿真与实际车间距对比图Fig.6 Comparison between model simulation and actual vehicle spacing of 019 vehicle

5 结论

对于驾驶行为的准确模拟是实现自动驾驶技术的重要前提，而驾驶行为存在随机性和不确定性，本文提出一种HMM结合随机模型预测控制的驾驶人跟车行为建模方法。建立驾驶人“感知-决策-操控”行为模型并应用多源数据采集和融合方法，利用自然驾驶数据实现HMM参数的辨识。自然驾驶数据表明：模型预测的车间距平均误差仅为1.47%。模型的建立为更好地满足智能网联环境下对于驾驶行为预测准确性和精确性的要求，为自动驾驶技术研发提供支持。

本文基于大样本量情况下频率近似概率的思想求解模型中状态概率分布列，因此，模型更适用于大数据采集下的交通场景。由于模型是对跟车行为进行模拟，模型应用时需将转向和换道行为车辆数据进行滤波处理，确保模型应用的准确性。