基于故障可诊断性的齿轮箱传感器优化布置

彭珍瑞， 刘 臻

(兰州交通大学 机电工程学院，兰州 730070)

齿轮箱作为调节转速和传递扭矩的旋转机械设备，其是否正常运行将直接决定机器能否正常工作。因此，有必要通过传感器来测得数据对齿轮箱进行状态监测与故障诊断，以便排除故障隐患，传感器优化布置就变得尤为重要。另外，若要达到对齿轮箱故障诊断的目的，前提是结构具有故障可诊断性。因此，寻找一组传感器集合，使其检测的数据能够达到期望的故障最大可诊断性就变得很有必要[1]。

近年来，国内外学者深入研究了传感器优化布置问题，但对于齿轮箱这类复杂机械设备传感器优化布置方面研究甚少。Kammer[2]提出有效独立法，以Fisher信息矩阵的行列式为优化目标，从全部自由度中逐步迭代删除对目标模态线性独立性贡献较小的自由度，保留对目标模态线性独立性贡献较大的自由度，直到得到较优的传感器布置方案。模态动能法的主要思想是在模态动能较大的位置处布置传感器，以提高结构模态测试时的信噪比，便于信号采集[3]。基于以上两种方法，很多人进行了改进，刘伟等[4]提出了有效独立平均加速度幅值法和有效独立模态动能法两种传感器优化布置方法，在考虑模态线性独立的同时能具有较高平均动态响应和模态动能。詹杰子等[5]提出了有效独立-改进模态应变能法，最终布置的传感器位置在具有模态独立性前提下，可以提高测点组合的抗噪性。还有人将智能算法引入到传感器优化布置中，以模态动能、模态信息矩阵的行列式、奇异值比值等作为优化目标，实现测点的优化[6-9]。文献[10]中仅安装了一些自身感兴趣变量的传感器，对于如何布置传感器具体安装数量及位置，以保证实现齿轮箱相关故障诊断方面没有针对性的研究。王桂兰等[11]从风机齿轮箱的动力学模型出发，将结构分析方法应用到齿轮箱传感器的优化配置中，实现传感器数量最少，识别、隔离可能出现的故障能力最大的配置目标。

以上传感器优化布置研究大多都集中于齿轮箱的模态观测性，而对齿轮箱可能发生的故障信号是否能被识别与分离研究较少，因此本文以齿轮箱有限元分析为基础，从实时测得齿轮箱运行状态信号出发，能更好的量化评价每一种故障的可检测性及与其他故障的可分离性。将故障可诊断性应用于齿轮箱传感器优化布置中，并将模态矩阵的奇异值比值、故障可诊断性、平均加速度幅值构成综合评价指标，对传感器数量和位置均进行优化，确定最合理的传感器布置方案，使得最终布置的传感器既反映齿轮箱的模态信息，还能对可能出现的故障实现识别与分离。通过ZDH10型齿轮箱故障诊断实验台实验，利用相关系数对实验结果进行验证，证明了所提方法的可行性。

1 基本理论

1.1 计算模型

对于一个具有任意自由度的线性系统，其运动方程为

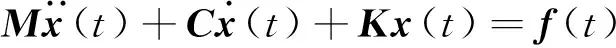
(1)

式中：M，C，K分别为质量矩阵、阻尼矩阵、刚度矩阵；f(t)为力向量；x(t)为响应向量。根据模态叠加原理，响应向量可以表示为

x(t)=Φq(t)

(2)

式中：Φ为模态振型矩阵；q(t)为模态坐标向量。

1.2 有效独立平均加速度幅值法

有效独立平均加速度幅值法(effective independent-average acceleration amplitude,EI-AAA)是针对有效独立法(effective independence，EI)所选取的测点没有较大的能量，从驱动点频响函数的近似表达式出发，推导出的一种传感器优化布置方法。为了使齿轮箱的初选测点集合不但具有尽可能高的平均加速度幅值，而且还要尽可能的保证测试模态具有较好的线性独立性。利用有效独立-平均加速度幅值法，即利用式(3)进行迭代，不断删除对目标模态独立性贡献较小且具有较低加速度响应的节点，即删除Hii接近于0的节点，保留对目标模态的线性独立性贡献较大且具有较大加速度响应的节点，即保留Hii接近于1的节点，直到达到所要求的传感器数目为止。

H=diag(Φ(ΦTΦ)-1Φ)·diag(ΦΦT)

(3)

1.3 K均值聚类算法

K均值聚类算法是一种迭代型聚类算法。本文中随着对齿轮箱有限元网格划分的细化，使得某些自由度在重要模态中的振型值相近，这些自由度在动力载荷下的响应也近似相等，这就会导致信息冗余。因此，采用欧氏距离式(4)作为相似性指标，将齿轮箱s个节点d阶振型的数据归为K类，进而可以有效地避免信息冗余问题[12]。

(4)

式中：K为聚类中心个数；s为节点数；Φi为第i个节点对应的振型；φk为第k个聚类中心振型。

1.4 核密度估计

核密度估计[13]是一种用于估计概率密度函数的非参数方法，本文用核密度对齿轮箱状态的频域信号进行密度函数估计。对于一组频谱数据{c1,c2,c3,…,cn/2}，其服从密度函数f(c)的分布，则f(c)的核密度估计为

(5)

式中，w为带宽；Kw(u)为核函数。本文选应用最广泛的高斯核函数为核函数

(6)

那么，f(c)的概率密度函数就可以写为

(7)

1.5 相关函数信息融合

相关函数信息融合是利用实测的两振动信号的相关函数来确定权值[14]。当传感器布置数量在两个及两个以上时，为了获得更全面的信息，需要将两个传感器采集的信息融合为一个。主要步骤如下：

步骤1利用传感器测得m个齿轮箱的运行状态信息X1(n),X2(n),…,Xm(n)。

步骤2利用互相关函数表达式式(8)对测得的每个信号分别与其余信号进行相关，相关程度越大，其对应的权值就越大。

步骤3采用相关信号的能量式(9)、式(10)来表征相关程度，即能量越大，相关程度越大。

步骤4通过式(11)确定各信号权重。由式(12)确定融合信号。

离散性随机振动信号的互相关函数表达式为

(8)

式中：N为信号长度；RXiXj直接反映两信号Xi(n)和Xj(n)之间的相关性。则振动信号的能量为

(9)

信号xi(n)与其他信号的总相关能量为

(10)

根据权值与相关函数的能量成正比原则得到

ρ1∶ρ2∶…∶ρm=E1∶E2∶…∶Em
ρ1+ρ2+…+ρm=1

(11)

由信号权重得到融合后的信号

X(n)=ρ1X1(n)+ρ2X2(n)+…+ρmXm(n)

(12)

1.6 故障可诊断性

故障可诊断性包括故障可检测性和故障可分离性[15-16]。本文中，故障可检测性FD(fi)指齿轮箱发生某种故障与未发生故障的概率密度函数的最小K-L散度值，故障可分离性FI(fi,fj)指齿轮箱发生某种故障与齿轮箱发生另外一种故障的概率密度函数的最小K-L散度值。K-L散度的计算公式为

(13)

式中，pi(c)和pj(c)为对两个不同故障的概率分布。故障可检测性FD(fi)可表示为

FD(fi)=min[K(pi‖pNF)]

(14)

式中：PNF为齿轮箱未发生故障的概率密度函数；pi为齿轮箱发生某种故障的概率密度函数。当FD(fi)越大，表明故障可检测性越强；当FD(fi)=0时，表示故障不能被检测。故障可分离性FI(fi,fj)可表示为

FI(fi,fj)=min[K(pi‖pj)]

(15)

式中，pi和pj为齿轮箱发生一种故障和另外一种故障的概率密度函数，当FI(fi,fj)越大时，表明故障fi和fj的可分离性越明显，当FI(fi,fj)=0时，表明故障fi和fj能被分离。

1.7 相关系数

若齿轮箱处于大致相同的故障状态，那么相同工况下采集到的振动信号在频谱上会有相似的密度函数曲线，而不同故障状态下振动信号频谱的密度函数曲线则有较大的差异，利用相关系数衡量密度函数曲线之间的相似性或者差异性。假定采集到齿轮箱某两种状态频谱的密度函数为f1(c)和f2(c)(c=1,2,3,…,n/2)则它们之间的相关系数为

(16)

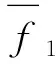
(17)

(18)

相关系数ρ12的取值范围为[-1,1]，其值越大，就表明两者相似度越高，反之，相似度就越差。

2 评价指标

目前，传感器的布置方案有多个评价指标，如奇异值比值、平均加速度幅值等，但这些都是反映齿轮箱的模态观测性，并不能反映齿轮箱中可能出现故障的识别与分离，因此，本文在评价传感器布置方案时，引入了故障可诊断性。另外，如果仅仅以奇异值比值、平均加速度幅值、故障可诊断性其中一个指标进行评价时，评价目标比较单一，仅仅只能考虑到一个因素，而合理的传感器布置，应需考虑多个因素。再加上这三者之间并不会发生冲突，因为故障可诊断性是从测点实时测得的信号出发，而奇异值比值和平均加速度幅值是从齿轮箱的振型出发，则故障可诊断性与奇异值比值和平均加速度幅值这两者之间分别独立，也就不会存在冲突；另外，平均加速度幅值准则是保证传感器能够布置在具有较大响应的节点处，而奇异值比值是尽可能的保证测点振型之间的正交性[17]，也就是保证各测点振型的独立性，并不会影响测点的加速度响应，则奇异值比值与平均加速度幅值是相互独立的，所以三个评价指标是相互独立的，并不会发生冲突。因此，本文将奇异值比值、故障可诊断性、平均加速度幅值三个评价准则构成综合指标评价，评价不同布置方案，确定最优传感器布置方案。

2.1 奇异值比值

模态矩阵的奇异值比(singular value ratio,SVR)作为判断传感器布置优劣程度的一项重要指标，为模态矩阵奇异值的最大值与最小值之比

(19)

式中：svd(·)为奇异值向量；Φ为所布置传感器构成的模态振型矩阵。为统一综合评价指标最大化，取S的倒数，具体函数转换为

(20)

f1越大则传感器布置效果越好。

2.2 平均加速度幅值

结构模态测试时一般都采用加速度传感器，传感器应该布置在具有较大的平均加速度幅值(average acceleration amplitude,AAA)的位置处，有利于数据的采集和提高测量的抗噪能力，计算公式为

Y=diag(ΦΦT)

(21)

式中，Y为一列向量，当所有元素都较大的时候，测点位置会较好。因此，建立平均加速度函数为

f2=mean(Y)

(22)

式中，mean(Y)为所布置位置的平均加速度幅值的整体平均值。

2.3 故障可诊断性

故障可诊断性是对齿轮箱可能发生故障可被检测和与其余故障可分离的综合体现，当每一种故障的可检测性和可分离性都较大的时候，测点的布置位置会较好，因此将故障可诊断性的平均值f3作为目标函数。

f3=mean(FD(fi)+FI(fi,f2)

(23)

2.4 综合评价指标

为避免某个指标信息被淹没的情况，对各个指标进行归一化处理并求和，即可得综合评价指标函数的表达式

(24)

式中，f为传感器布置结果的综合体现，如果综合评价指标越大，说明各项评价指标都较好，传感器布置更合理。

3 传感器优化布置

由于目前大多数的研究都集中于齿轮箱的模态观测性，而当齿轮箱发生某种故障时，故障是否能更容易检测到并将它们区分开，研究较少，也就是说当传感器布置在哪个位置处(如输入端、输出端等)时，既能够检测到这种故障，又能将这种故障与其余故障更好的辨识出来。因此，为了使安装的传感器获取的信息不但可以反映齿轮箱的模态信息，还能对可能出现的故障实现识别与隔离，构建了一种基于故障可诊断性的齿轮箱传感器优化布置方法，其流程如图1所示。

图1 传感器优化布置流程图Fig.1 Flow chart of optimal sensor placement

3.1 初选测点

先建立齿轮箱有限元模型，进行模态分析，提取齿轮箱的模态振型。由于有限元网格划分精细，大部分自由度有相似的动力特性，会引起信息冗余。本文根据自由度在重要模态中振型值的相似性，使用K均值聚类算法按隶属度对有限元划分的节点进行自动分类，将动力特性相似的自由度划分为一簇。在每一簇中再利用有效独立-平均加速度幅值法选出精英个体(即所含振动信息丰富的自由度)，再将这些精英个体组为一体，再从这些精英个体中选出具有较大平均加速度幅值和较大模态独立性的节点作为初选测点。对齿轮箱节点聚类步骤如下：

步骤1从所提取的齿轮箱振型矩阵中随机选取K个节点所对应的振型作为最初的聚类中心。

步骤2根据每个节点所对应的振型与这些聚类中心的欧氏距离，将节点分到距离最近的聚类中心所对应的类中。

步骤3更新聚类中心，即求得每一类中所有元素的均值，并将其作为新的聚类中心。

步骤4判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回步骤2。

3.2 故障可诊断性判断

首先，由3.1节初选的节点找到实体中齿轮箱所对应的位置。并在所有的初选位置上分别布置传感器，测得齿轮箱正常的以及可能发生故障(如主动轮断齿、从动轮磨损等)的状态信号，其次，对测得的信号进行快速傅里叶变换得到其对应的频谱图，接着对其频谱图进行核密度估计式(7)求得概率密度函数。最后，用式(14)确定其对应故障的可检测性；用式(15)确定故障的可分离性，用式(23)确定在每一个节点处的故障可诊断性。

由动态规划算法的思想，选择故障可诊断性最大的节点位置，然后确定此节点位置，再从剩余的节点中分别与其两两组合测得可能发生故障的信号，然后将这两个位置的信号利用相关函数数据融合算法[13]进行信息融合，再利用核密度估计对其分别进行概率密度函数估计，确定它们的故障可诊断性，再选择故障可诊断性最大的两个节点位置组合，然后确定这两个节点位置，依次确定第三个、第四个，直至所有初选测点进行信息融合并确定它们的故障可诊断性为止。

假设初选测点是A，B，C，D四个位置，有a(正常)，b，c，d四种状态。具体的故障可诊断性步骤：

步骤1分别在A，B，C，D这四个位置处，测得a，b，c，d四种状态的信号。

步骤2对在每一个位置测得的信号进行快速傅里叶变换得到其对应的频谱图，利用核密度估计求得它们的概率密度函数。

步骤3求b，c，d的概率密度函数与正常信号(a)概率密度函数之间的K-L散度值确定其对应故障的可检测性；再分别求b，c，d两两之间概率密度函数之间的K-L散度值，确定故障的可分离性，进而确定在每个节点处的故障可诊断性。

步骤4选择故障可诊断性最大的位置，确定此位置并分别与其余位置组合，判断各组的故障可诊断性。假如A最大，就确定A位置，继续判断A与B，A与C，A与D的故障可诊断性。当确定的位置在两个及两个以上时，对测得的信号进行信息融合。

步骤5返回步骤2，直到初选测点组合完成为止，也就是A，B，C，D四个位置组合完为止。

3.3 综合指标确定布置方案

当需要确定最合理的传感器数目时，应使用尽量少的传感器来使得各目标函数值均较好。合理的传感器布置应该综合考虑各项指标，因此，以奇异值比值、平均加速度幅值和故障可诊断性构成的综合评价指标式(24)对由3.2节确定的节点位置进行评价，最终确定传感器最优布置位置。

4 应用实例

4.1 齿轮箱主要参数

齿轮箱试验台主要由伺服电机、ZDH10型齿轮箱、磁粉制动器组成，如图2所示。以ZDH10型齿轮箱为研究对象，其具体参数：材料为HT150，其泊松比为0.25，密度为7 100 kg/m3，弹性模量为1.5×1011Pa。在齿轮箱的各零件中，齿轮故障所占的比例最大，能达到60%以上。因此本文就齿轮可能发生的故障进行故障可诊断性判断，齿轮具体参数如表1所示。齿轮状态如表2所示。可能发生的故障如图3所示。选取INV982X系列的压电式加速度传感器。

图2 故障诊断装置Fig.2 Fault diagnosis setup

图3 齿轮故障Fig.3 Gear fault

表1 齿轮参数Tab.1 Gear parameters

表2 齿轮状态Tab.2 Gear state

4.2 齿轮箱传感器位置初选测点

依照图纸在Solidworks中建立ZDH10型齿轮箱的实体模型，然后导入ANAYS Workbench 17.0进行网格划分，计算前6阶模态，提取振型矩阵。将齿轮箱箱体划分为10 207个节点，5 143个单元。首先根据各节点振型的动力相似性，利用K均值聚类将节点聚为4类，对每一类用EI-AAA法筛选出100个节点。再将每一类的100个节点集结在一起，用EI-AAA法从这400个节点选择5个节点，作为初选测点。具体初选的测点位置如表3所示。节点对应测点位置如图4所示。对应在故障实验台上的具体位置如图2所示。

表3 初选测点位置Tab.3 Initial measuring points

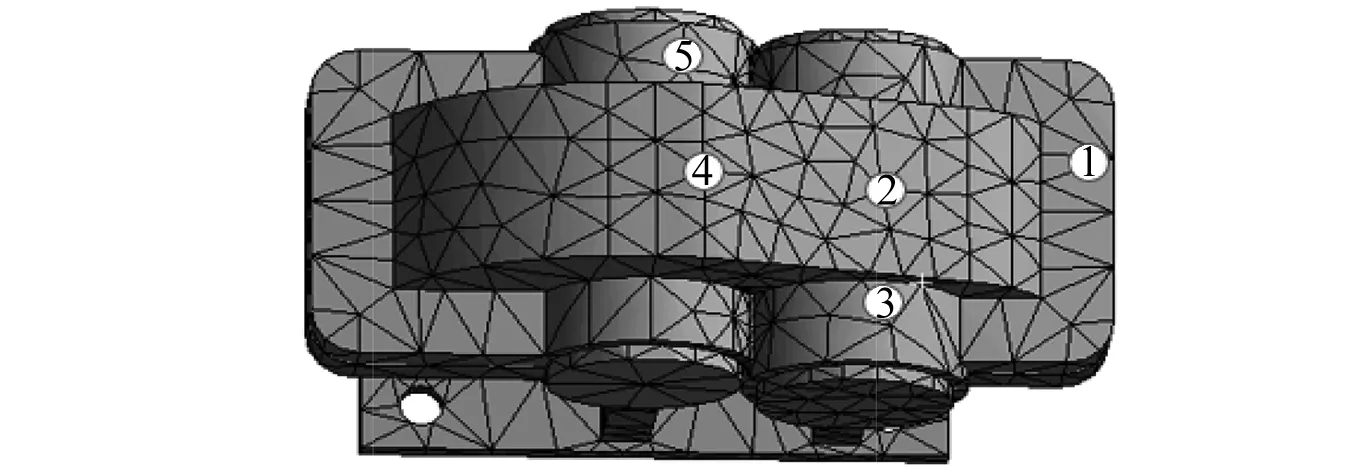
图4 初选测点位置Fig.4 Initial measuring points

4.3 故障可诊断性判断

在实验中，驱动电机的转速为348 r/min，磁粉制动器的施加电流为0.1 A，采样时间为6 s，采样频率5 kHZ，振动传感器测量齿轮箱垂直方向上的振动数据，当传感器布置在节点7460、节点6579、节点7788时，齿轮箱表面都比较平整，可以直接将传感器贴在上方。在节点6925(输入端)和节点9121(输出端)处布置传感器时，会存在传感器在节点的左侧和右侧(背对伺服电机)两种偏移情况，通过试验发现在这两个位置处，测得的信号基本一样，因此就将传感器布置在较为平整的一边，输入端在左侧较平整，输出端在右侧较平整。

4.3.1 确定第一个位置

分别在节点7460、节点6959、节点6925、节点7788和节点9121处，测得F1，F2，F3，F4和F5五种状态的信号，进行核密度估计，以节点7460为例，其对应的频谱及其核密度估计图如图5所示，然后利用K-L散度确定F2，F3，F4，F5四种故障的可检测性与可分离性，具体数值如表4所示。

表4 故障可诊断性量化评价Tab.4 Quantitative evaluation of fault diagnosability

图5 五种状态下的频谱图及其对应的密度函数Fig.5 Spectrum and their corresponding density functions under five states

当在节点6925处时，故障可诊断性的均值最大，确定第一个位置为：节点6925。

4.3.2 确定第二个位置

在确定第一个位置的基础上，继续判断节点6925+节点7460、节点6925+节点9121、节点6925+节点7788、节点6925+节点6579的故障可诊断性。当判断以上两个节点位置的故障可诊断性时，分别测得各组节点F1，F2，F3，F4和F5等五种状态的信号，并进行对应状态的信息融合，再对融合信号的频谱图进行核密度估计，进而确定四种故障的可诊断性，具体数值如表5所示。

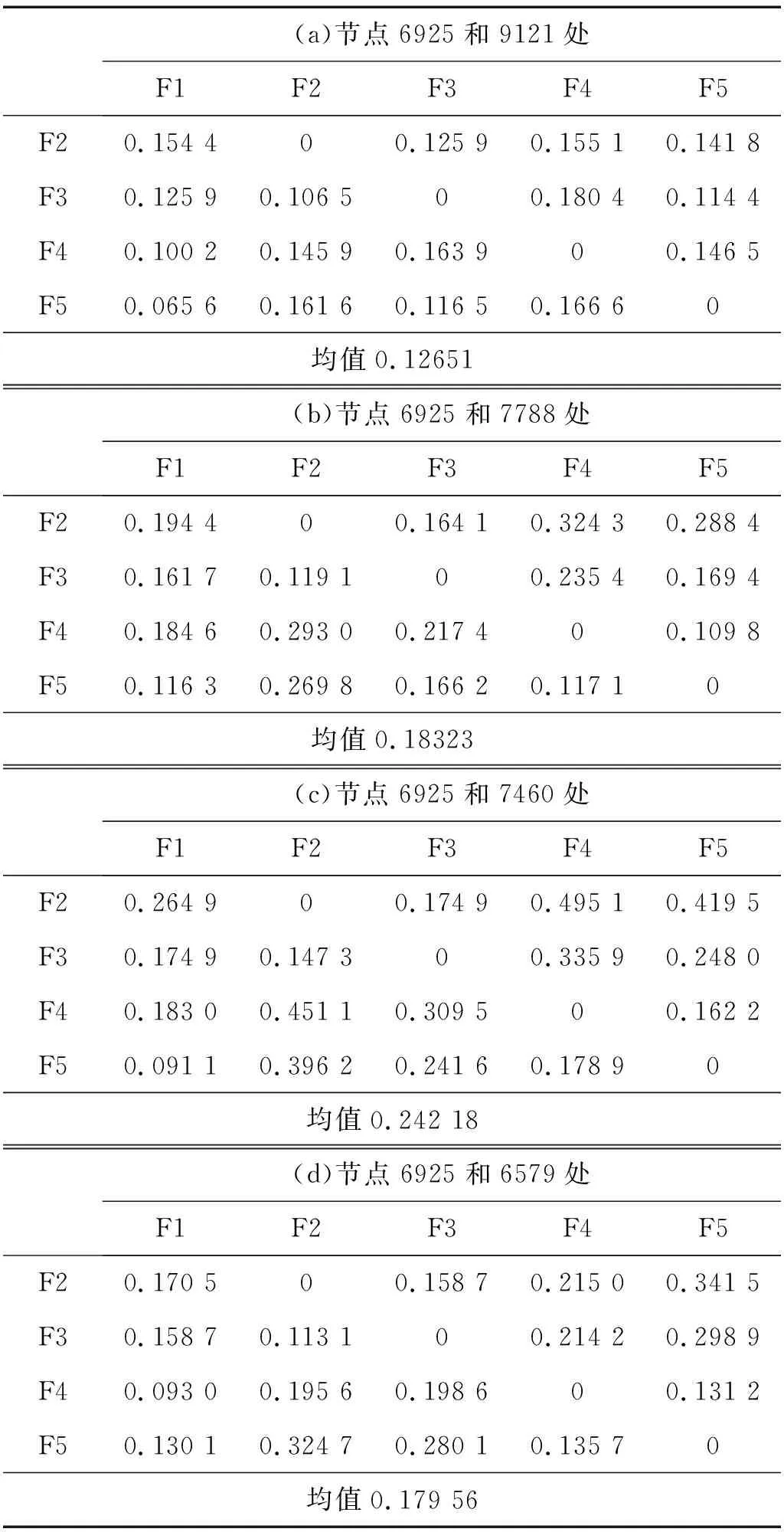
表5 两信号融合下的故障可诊断性量化评价Tab.5 Quantitative evaluation of fault diagnosability based on two-signal fusion

当传感器布置在节点6 925和7 460处时，故障可检测性和故障可分离性的均值最大，因此确定前两个位置即：节点6925+节点7460。

4.3.3 依次确定第三、第四、第五位置

在前两个位置的基础上，然后继续判断节点6925+节点7460+节点9121、节点6925+节点7460+节点7788、节点6925+节点7460+节点6579。由于篇幅限制，就没列举具体数值。当在节点7788+节点7460+节点6925处时，故障可检测性和故障可分离性的均值较大，因此，确定前三个位置即：节点6925+节点7460+节点6579，接下来继续判断节点6925+节点7460+节点6579+节点9121、节点6925+节点7460+节点6579+节点7788。当在节点6925+节点7460+节点6579+节点7788处时，故障可检测性和故障可分离性的均值较大，确定传感器前四个位置即节点6925+节点7460+节点6579+节点7788；然后确定节点6925+节点7460+节点6579+节点7788+节9121的故障可诊断性。具体故障可诊断性变化图如图6(b)所示。

4.4 综合评价确定方案

根据故障可诊断性得到布置不同数量的传感器对应的不同布置结果，首先根据式(19)，式(22)计算出不同布置方案对应的奇异值比值、平均加速度幅值。利用式(24)对不同的传感器布置方案进行综合评价，确定最优传感器布置方案。具体评价结果如表6所示，则选择两个传感器即节点6925和节点7460时齿轮箱的故障可诊断性和模态可观测性最大。

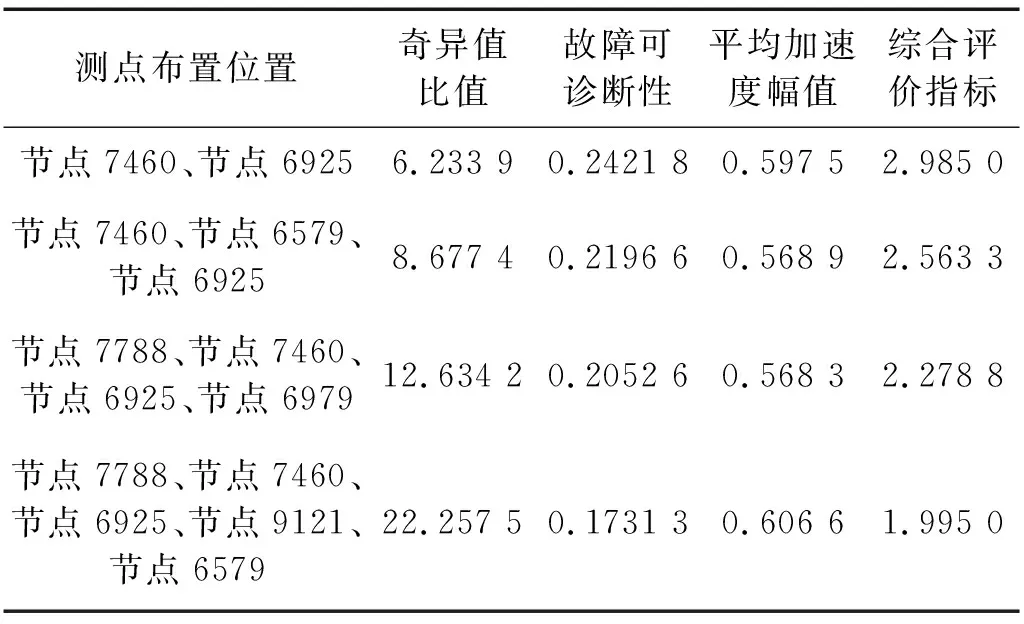
表6 综合评价指标Tab.6 Comprehensive evaluation index

单个评价指标结果如图6所示，如果仅仅以奇异值比值(判断两测点振型的正交性，测点至少有两个，因此从2开始)、平均加速度幅值、故障可诊断性其中一个进行评价时，奇异值比值是在布置两个传感器(即节点6925和7460)时，效果较好，如果存在冲突，平均加速度幅值和故障可诊断性在两个(即节点6925和7460)测点时，效果会最差。而在两个测点时，平均加速度幅值和故障可诊断性的值都较大，即效果较好，则这个评价指标之间不存在冲突。因此，利用综合评价指标能更好地量化评价传感器位置。由图6也可知，当传感器布置在两个节点时，奇异值比值和故障可诊断性都最好，平均加速度幅值也仅次于最好值，也印证了综合评价指标的合理性。

图6 三个评价指标Fig.6 Three evaluation indexes

4.5 方法对比

当利用有效独立平均加速度幅值法直接对齿轮箱进行传感器优化布置时，得到的节点位置为节点9121和节点7788，故障可诊断性均值为0.187 22，远小于在节点7460和节点6925处的值。具体故障可诊断性量化评价如表7所示。

表7 EI-AAA法故障可诊断性量化评价Tab.7 Quantitative evaluation of fault diagnosability by EI-AAA

4.6 结果验证

为了证明在节点6925和节点7460两个位置处，所布置传感器的合理性，分别测得齿轮箱F1，F2，F3，F4，F5的状态信号，进行核密度估计，并求它们在这两个位置处两两之间的概率密度函数的相关系数。当他们之间的相关系数越小，即相关度越低，说明两种故障越容易区分。相反，这两种故障越难区分。为了证明在节点6925和节点7460比其他位置更为合理，与其他三种布置方案进行比较，相关系数评价如表8所示，当在节点6925和节点7460两个位置处时，他们之间的相关系数最小，任意两故障也更容易区分。从而也证明了传感器在节点6925和节点7460两个位置处布置的合理性。

表8 相关系数评价Tab.8 Correlation coefficient evaluation

5 结 论

本文构建了一种齿轮箱故障可诊断性的传感器优化布置方法，以ZDH10型齿轮箱为例进行传感器优化布置，获得了较好的布置效果。

(1) 利用K均值聚类算法和有效独立平均加速度幅值法从各聚类自由度中选择出所含信息较丰富的自由度作为待选测点，能够有效避免信息冗余。

(2) 将多个传感器信息进行信息融合，并利用核密度估计对其对应的频谱进行密度函数估计，再利用K-L散度进行故障可诊断性判断，确定每一种可能发生的故障的可检测性和可分离性。

(3) 通过使用由模态矩阵的奇异值比值、故障可诊断性、平均加速度幅值构成的综合评价指标对传感器数量和位置进行了优化，综合考虑了各方面因素，可获得最合理的传感器布置方案。