爆炸冲击荷载下扩腔体积和能耗随抵抗线的变化规律研究
雷 振, 黄永辉, 陈文梦, 张智宇, 周继国
(1. 贵州理工学院 矿业工程学院,贵阳 550003; 2. 昆明理工大学 电力工程学院,昆明 650500;3. 昆明理工大学 国土资源工程学院,昆明 650093)
随着工业技术的高速发展,工程爆破正在向着科学化、精细化和数字化方向发展,诞生了很多先进的理论和技术,主要涉足的研究和应用领域有:民用爆炸物品和起爆方法的高端化研究,工程爆破施工装备的先进化研究,基础爆破理论的完善和突破方面的研究,数值模拟技术的准确化研究,工程爆破的精细化控制方面的研究等。然而,因炸药爆炸具有瞬时、高温、高压等极端态特性,关于爆破破岩过程中,能耗的精准统计和分布规律是学术界一致公认的难题。
近年来Whittles等[1]对岩石破碎特性进行了试验与数值模拟,研究了应变率、冲击能、破碎度和破碎能效率之间的关系。Hamdi等[2]介绍了一种用于评价工程爆破中岩石破碎能量的新方法。吴亮等[3]依据材料力学、岩石力学理论,从爆破能量整体分布角度出发获得了柱状药包临界埋深以下的爆破能量做功分布占比:冲击波能耗约为40%,爆轰气体中用于扩腔和裂纹扩展的能耗约为23%。顾文彬等[4]以阻抗匹配作为分析角度对耦合、空气不耦合、水不耦合三种装药结构下的爆破能量传递规律进行研究,表明不耦合装药条件下存在合理的不耦合系数使得爆破能量可以高效作用于岩石。肖思友等[5]对高地应力下爆破荷载和动态卸载效应对破岩效果和损伤破坏范围的影响进行了研究,基于断裂力学与破碎能量准则计算出了爆破荷载下岩石破碎块度与岩石损伤范围。宗琦等[6-7]通过分析爆炸能量的折射和反射规律,建立了爆炸能量折射率和反射率的计算公式以及岩石和炸药的最佳阻抗匹配关系,探讨了不同装药方式对爆破能量传递效率的影响。韩亮等[8-12]对台阶、大爆破等情况下冲击波和爆破振动传播规律进行研究。
然而对于爆炸时扩腔能以及抵抗线对扩腔能的影响规律方面的研究并不多见。
基于上述原因,本文采用断裂力学能耗理论和基础模型实验的方法,围绕爆炸扩腔能耗计算方法及不同抵抗线扩腔能的变化规律开展研究,该研究对精细化控制爆破理论和技术的应用具有实际意义。
1 扩腔能耗计算方法
无限区域介质中,炸药产生爆炸之后,会在炮孔附近迅速形成爆炸空腔,同时在周围不同范围的介质形成粉碎区、裂隙区,并在远区介质引起弹性变形,形成弹性振动区。
台阶爆破时,岩石介质存在自由面,炸药埋深小于“临界埋深”,炸药处于半无限介质区域之中,炸药在炮孔内部产生的冲击波与爆生气体同样会对周围岩石造成粉碎,形成爆腔,如图1所示。炸药所形成的爆炸空腔造成了矿岩的粉碎,从炸药能量利用角度考虑,该部分能量造成了矿岩的粉碎,易导致矿石损失,增加矿石贫化,属于无用能。台阶爆破时,炮孔数量众多,众多爆腔的形成会造成大部分能量的耗散与矿岩粉碎,而爆破参数的变化通常会改变爆腔形态以及炸药能量用于爆腔能耗的分布。因此,对于不同爆破参数下的爆腔能耗的研究具有重要的现实意义。
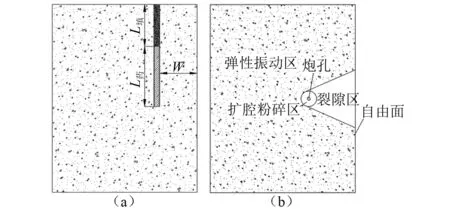
图1 台阶爆破岩石状态分布图Fig.1 Bench blasting state of rock
岩石和混凝土动态损伤和动态强度方面,冯君等[13-18]利用SHPB等相关设备进行了研究。对于爆炸荷载下岩石和混凝土损伤,一般认为炸药在爆轰之后,迅速在炮孔周围激起超声速的爆炸冲击波,此时周围岩石受到剧烈压缩,冲击波开始对岩石做功,孔壁周围岩石质点发生位移形成爆腔,炮孔直径增大,随着岩石被逐渐粉碎,冲击波所携带的能量迅速被损耗,并迅速衰减,在冲击波到达粉碎区边缘时,冲击波衰减为应力波,其对岩石的压缩结束,冲击波所引起的爆炸扩腔过程结束;继冲击波作用之后,炸药所产生的爆生气体迅速膨胀,并继续以准静态压力的形式作用在爆腔孔壁上,产生膨胀对岩石做功,导致腔壁岩石质点继续产生径向移动,爆腔在此压力之下继续产生扩张,爆腔体积进一步增大,爆生气体压力在对岩石做功之后逐渐降低。当炸药埋深小于“临界埋深”,巨大的爆生气压会贯穿岩石自由面,此时气压力下降到与周围的围岩压力相均衡,爆腔扩张过程结束。
所以爆腔形成过程分为两个阶段,第一阶段冲击波扩腔,将炮孔半径r0扩增到r1;第二阶段爆生气体继续扩增,最终爆腔半径达到r2,如图2所示。其能量来源于冲击波以及爆生气体,表示为
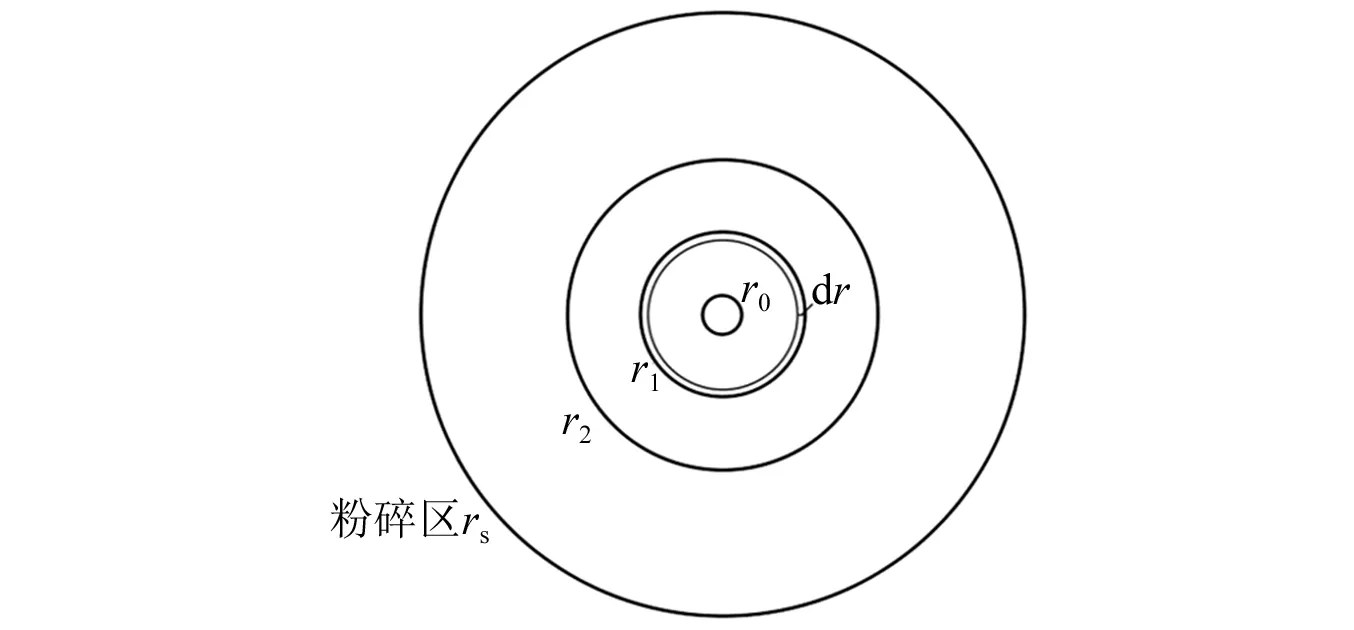
图2 爆腔示意图Fig.2 Explosion cavity
Ec=Es+Eg
(1)
式中:Es为冲击波扩腔做功,J;Eg为爆生气体扩腔做功,J。
冲击波压力以及爆生气体压力在衰减至岩石动态抗压强度之前,它们的压力值都大于岩石动态抗压强度,衰减至低于岩石动态抗压强度后,二者压缩岩石产生扩腔作用的能力丧失,所以其对于岩石所产生的有效做功均为克服岩石动态抗压强度做功,爆腔形成所需炸药能量即为二者克服岩石动态抗压强度做功所消耗的能量。因此,从岩石自身角度出发,冲击波与爆生气体的扩腔作用可视为相同过程,即岩石的整个压缩过程。
(1) 冲击波扩腔能计算
将r1范围内的介质沿径向划分为若干微元体,各微元厚度为dr,如图2所示,则某微元受冲击波所做的功可表示为
dEs=2πrlcσrdr
(2)
式中:r为微元dr对应的半径;lc为柱状爆腔轴向高度;σr为冲击波压应力,随着扩腔的进行,会发生不断衰减,为关于r的函数。
由两部积分转换为
(3)
式中:r1为炮孔直径;r2为最大扩腔直径。
(2) 爆生气体扩腔能计算
某微元体受爆生气体所做的功为
dEg=2πrlcPdr
(4)
式中,P为爆生气体膨胀过程的瞬时压力,随气体的膨胀压力不断衰减,也是关于r的函数。Eg可表示为
(5)
(3) 简易计算方法
将爆腔rc范围内的介质沿径向划分为若干个微元体,各微元厚度为dr,如图2所示,则压缩某微元,克服其动态抗压强度所做的功可表示为
dE=2πrl0σcddr
(6)
所以,炸药径向压缩岩石能耗可表示为
(7)
式中:l0为柱状装药高度;lc为柱状爆腔轴向高度。
实际爆破中,柱状药卷在轴向上也会对岩石产生粉碎压缩,其能耗为
(8)
将轴向与径向压缩的能耗相加,得到Ec计算方法为
(9)
式中:r为微元dr对应的半径,m;lc为柱状爆腔轴向高度,m,可通过实验测量得到;σcd为岩石动态抗压强度。
2 模型试验方案和基础力学测试
2.1 试验方案
模型试验以研究台阶爆破过程中炮孔扩腔能耗随最小抵抗线的变化规律为目的,因此前提条件假定为:炮孔直径、装药量、装药长度、浇筑模型的材料配比和强度均不变。尽量保证实验工艺精细化,每组试验浇筑三个模型,统计结果取平均值,减少实验过程的人为误差。
浇筑模型的试验材料采用普通硅酸盐水泥作为模型胶结材料,粒径为0.35~0.50 mm的石英砂为模型骨料,材料配比选择水泥、石英砂、水的质量比1∶5∶1,模型尺寸:长600 mm,宽600 mm,高650 mm,炮孔直径10 mm。待模型制作完成且湿养一周,并在自然环境下养护28 d后再开展实验。浇筑的试验模型如图3所示。

图3 试验模型图Fig.3 Test model
2.2 模型制作及材料性能测试
模型材料力学性能测试中浇筑15个尺寸为100 mm与模型材料配比、保养过程完全一致的试件,进行基础力学性能测试,测试过程如图4所示。

图4 标准试件物理力学参数测试Fig.4 Division diagram of explosion cavity
分别测试材料的密度、纵波波速、单轴抗压强度、泊松比,试件的主要物理力学参数测试结果如表1所示。

表1 材料物理力学参数Tab.1 Physical and mechanical parameters of materials
2.3 爆破参数
模型试验选在云南民爆集团安宁化工厂的试验场地,在浇筑模型时预留炮孔,孔深由装药长度、雷管长度和填塞长度三部分构成,其中雷管长65 mm,装药长度40 mm,填塞长度等于最小抵抗线;炸药单耗采用公式
qm=Q/LW2
(10)
工业炸药采用药芯为黑索金的导爆索,导爆索每米装药量25 g,炸药性能参数如表2所示,雷管选用8号瞬发电雷管,其中猛炸药量0.58 g,详细的爆破参数如表3所示。炸药爆炸作功的过程是极其迅速的,可以假定炸药爆轰生成的高温高压气体进行绝热膨胀作功,根据热力学第一定律,系统内能的减少等于系统放出的热能和系统对外所做的功,研究扩腔能耗及其在炸药爆炸过程中总能量的占比,总能量采用爆热和炸药量的确定方式。模型养护达要求后进行反向装药爆破试验。

表2 炸药性能Tab.2 Explosive performance
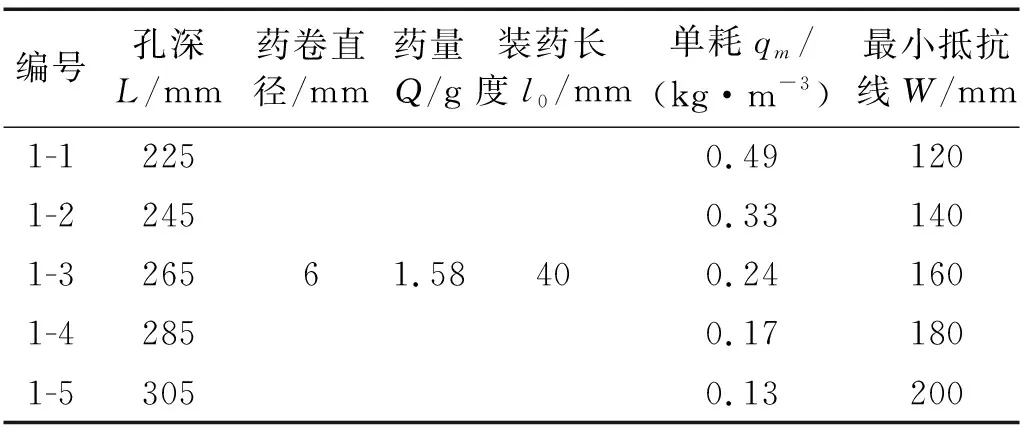
表3 爆破参数Tab.3 Parameters of blasting
3 爆炸荷载下扩腔规律
3.1 爆腔体积变化规律
为减少实验误差,每种抵抗情况下至少进行三组实验,在爆破试验完成之后,部分模型爆腔形态如图5所示,爆炸发生时,炮孔壁岩石受到爆炸产物巨大的冲击荷载,远远大于岩石的抗压强度,在此荷载下周围岩石发生压缩性粉碎,产生不可逆破坏,炮孔直径发生增大,形成大于炮孔原有体积的爆腔。
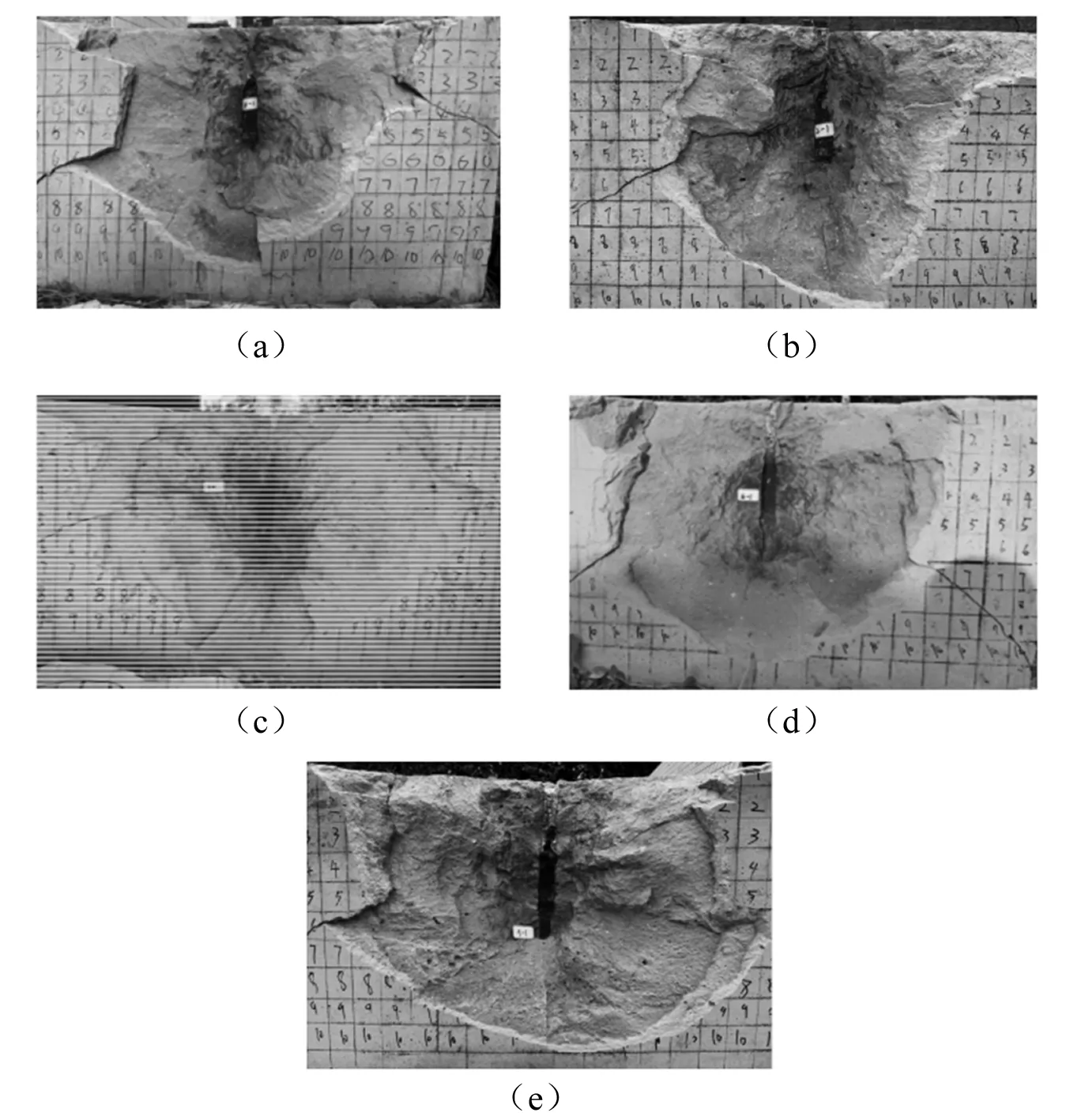
图5 爆腔形态图Fig.5 Shape of cavity
在爆破试验完成之后,对各个模型炮孔所形成的爆腔进行半径与轴向长度的统计,排除误差较大实验结果,采用测试结果相差不大情况下的平均值作为实验结果,得到各抵抗线爆腔相关参数如表4所示。其中炮孔周围岩石扩腔体积Vc通过式(11)进行计算
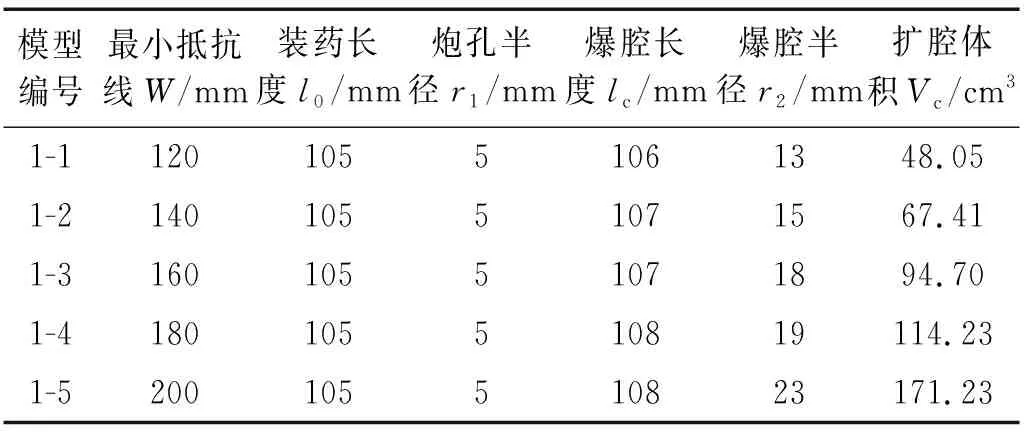
表4 爆腔试验结果表Tab.4 The table of blasting chamber test results
(11)
不同抵抗线情况下的模型试验结果显示:
(1) 随最小抵抗线的增大,爆腔在炮孔轴向方向上的长度基本未产生变化,其大小几乎与装药长度相同,表明柱状药卷在轴向上的扩腔长度和对岩石造成的粉碎破坏范围与抵抗线变化关系不大,最小抵抗线的变化对炸药在轴向的做功影响很小。
(2) 随着最小抵抗线的增大,爆腔半径逐渐增大,岩石过度粉碎的扩腔区域体积明显增大,当抵抗线由120 mm增加到200 mm时,爆腔半径由13 mm增加到23 mm,炮孔半径的倍数由2.6倍增加到4.6倍,符合粉碎区半径一般约为药包半径的2.5~4.7倍条件;扩腔体积由48.05 cm3增加到171.23 cm3,抵抗线增加1.67倍而扩腔体积增加3.56倍,呈现指数增长态势,详情如图6所示,表明最小抵抗线的变化对于柱状药卷在径向的粉碎作用产生了较大影响,减小最小抵抗线长度可减小矿岩的过度粉碎区域,降低无用功。
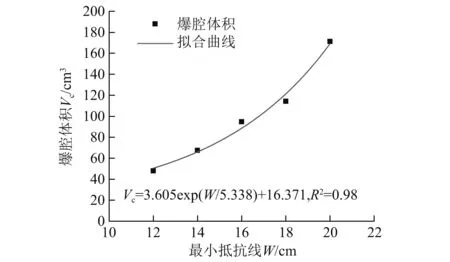
图6 不同抵抗线爆腔体积变化趋势图Fig.6 The change trend of the volume with the minimum holdout line
3.2 爆腔能耗规律
此次试验爆破对象为素混凝土,根据相关文献研究成果,动态抗压强度取静态抗压强度的1.3倍,σcd=10.89 MPa,根据文中构建的爆腔能耗计算方法对爆腔扩张所需能量进行计算,获得了不同抵抗线情况下的爆腔扩张能,具体数值详如表5所示。
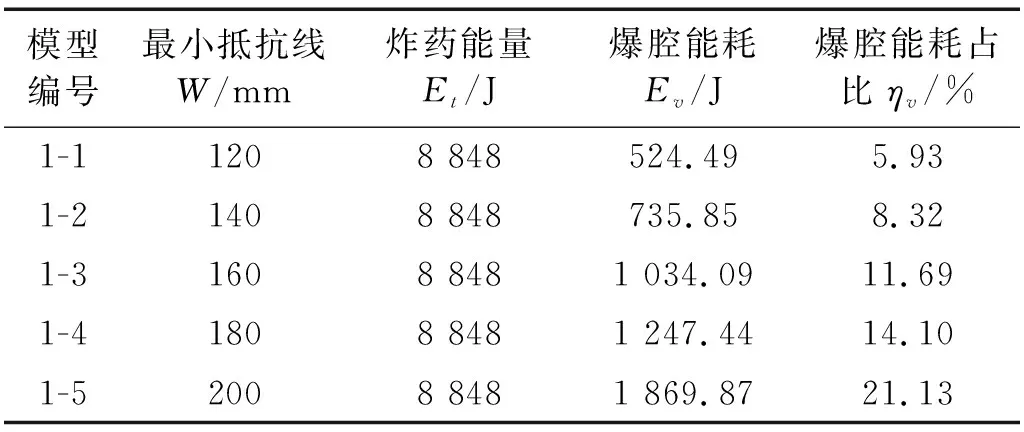
表5 爆腔能耗表Tab.5 The table of energy consumption
爆腔能耗随最小抵抗线变化关系,可见随着最小抵抗线的增大,用于岩石粉碎的能耗会逐渐增大,当最小抵抗线为120 mm时,粉碎能耗约524 J,而当最小抵抗线增大到200 mm时,岩石粉碎能耗达到了1 870 J,同样达到最小抵抗线为120 mm时的3.56倍,说明最小抵抗线的变化在较大程度上影响着爆腔扩张所消耗的能量,最小抵抗线越大,爆轰产物所受约束作用更大,对岩石的压缩粉碎作用的时间更长,更多的能量用于爆腔的扩张,炸药对于破碎岩块的抛掷作用以及抛掷动能占炸药能量比例皆会发生下降。扩腔体积和扩腔能满足式(12)的分布规律
Ec=σcdVc
(12)
表明当岩石动态抗压强度确定时,爆腔能耗与爆腔体积成正比,而随着最小抵抗线的增大,爆腔体积逐渐增大,所以爆腔能耗随最小抵抗线增大是由于爆腔体积逐渐增大所导致的。对最小抵抗线与爆腔能耗关系进行拟合得到两者存在幂函数关系如图7所示。
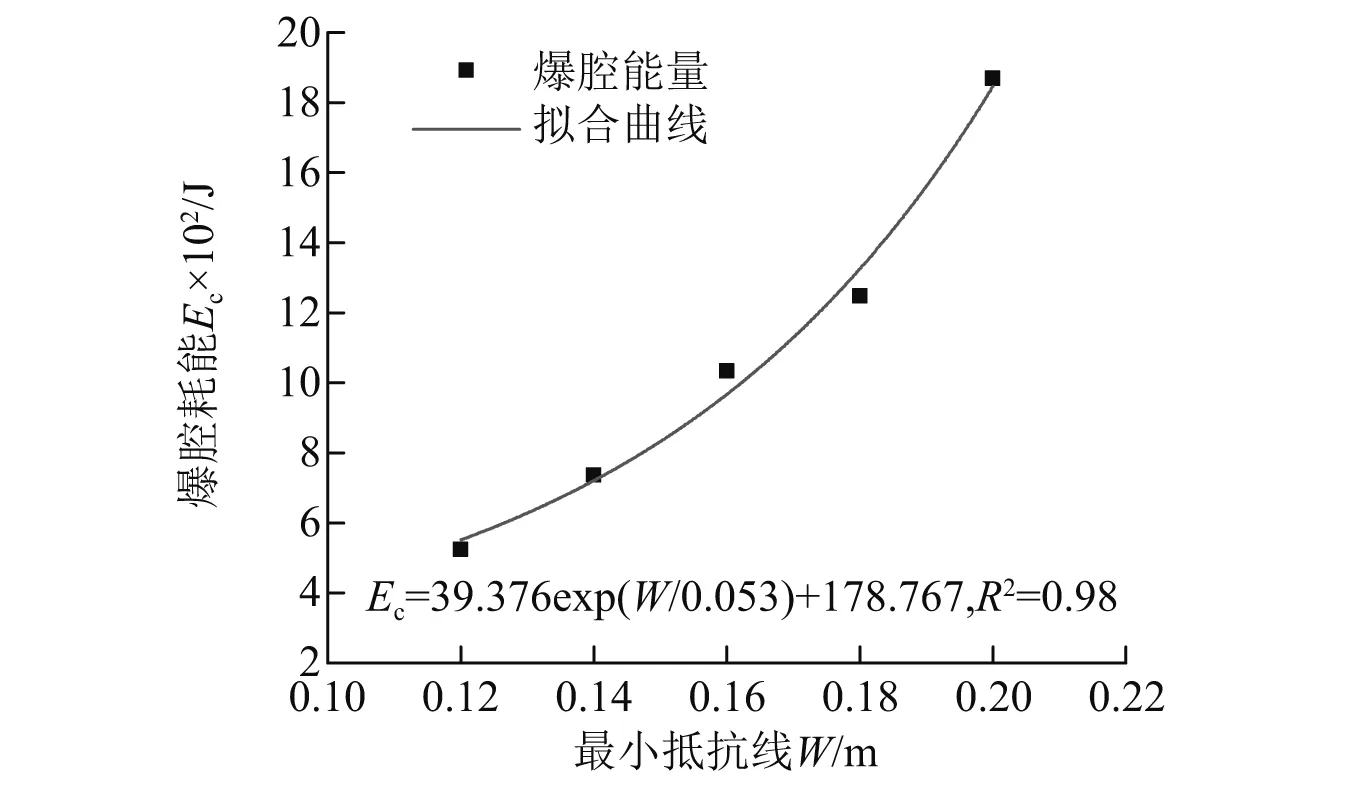
图7 爆腔能耗随最小抵抗线变化关系Fig.7 The change trend of cavity expansion with the minimum holdout line
并利用式(13)对爆腔能耗占比进行计算
ηc=Ec/Et
(13)
计算结果见表5。计算结果充分反映了不同抵抗线情况下爆腔能耗的准确占比和变化关系,炸药能量用于扩张爆腔的比例介于5%~21%,随最小抵抗线增大逐渐增大。说明装药量一定时,最小抵抗线的大小影响爆破能量对炮孔周围介质的作用效应,最小抵抗线的增大会增加炸药能量用于粉碎岩石的比例,导致爆腔体积的增大,改变炸药的能量分布。
4 结 论
通过基础理论分析和大量的模型试验获得了炮孔内炸药爆炸荷载下炮孔周边岩石过度粉碎区即爆腔体积随着最小抵抗线的变化规律:
(1) 运用动态抗压强度,构建了炮孔周边岩石扩腔过程中过度粉碎区岩石破碎能耗的简易计算公式,利用计算公式对模型试验中扩腔能耗的计算结果在合理的范围内,验证了计算公式的可行性。
(2) 扩腔影响范围主要在朝向自由面的径向方向,最小抵抗线增大会延缓台阶自由面鼓包作用发生的时间,使爆炸产物与岩石相互作用时间延长,增强其对于岩石的粉碎作用,导致爆腔半径、爆腔体积和扩腔能耗的增大,呈明显的指数增长趋势。
(3) 炮孔周边区域岩石介质的过度破碎能耗及其在炸药爆炸过程中的占比,直接关系到工程爆破时能量利用率和爆破效果。
如何精准获得工程爆破中能耗的占比和提高有用功的问题一直是难题,文中仅研究了最小抵抗线的影响规律,未考虑其它影响因素。最小抵抗线和其它爆破参数以及岩石介质性质的耦合影响规律待进一步研究。

