大前进比变转速旋翼气弹动力学建模与载荷特性分析

余智豪， 周 云， 宋 彬

(中国直升机设计研究所 直升机旋翼动力学重点实验室，江西 景德镇 333001)

变转速旋翼为当前研究热点，未来直升机发展中也有多处采用变转速旋翼技术[1]。一方面降低旋翼转速能有效提高旋翼升阻比，并能降低旋翼需用功率和耗油率[2-3]，从而达到提高航程的目的，波音公司采用优化旋翼转速概念(optimum speed rotor, OSR)[4]研制A160T[5-6]长航时无人直升机，创下续航时间、航程、降噪等多项记录；另一方面，共轴高速直升机采用变转速技术，通过降低旋翼转速有效推迟前行激波产生，实现高速前飞，Sikorsky针对军方“未来垂直起降飞行器”项目而研制的S-97侵袭者目前已突破370 km/h前飞速度。该构型的高速直升机未来还有巨大的发展前景[7-8]。

随着长航时直升机以及共轴高速直升机的研制成功和发展，越来越多的团队开展了变转速旋翼方面的研究工作。虽然采用变转速技术能提升直升机性能和提高前飞速度，但同时也出现复杂的气弹动力学问题。旋翼转速降低和前飞速度增加使得反流区扩大，该区域的桨叶段处于负迎角状态，存在动态失速以及负升力现象，这对反流区气动力计算提出更高要求。Chopra团队[9]在研究大反流区气动力计算时提出对动态失速模型进行修正，进而提高计算精度。另有研究[10]表明通过修正L-B模型中的迎角以及变距运动，修正有效分离点和临界法向力系数的方法能拓展模型适用范围，在大反流区内取得较好的气动力计算精度。另外大前进比下反流区扩大，气动载荷分布发生改变，国外团队在研究UH-60全尺寸变转速试验[11]当中发现：随着反流区的扩大，旋翼为满足配平会造成桨叶内外段气动载荷差距增大，同时反流区内的负升力区域以及反流区内气动中心位置的改变会造成桨叶内外段的扭矩差异，使得桨叶产生周期性的脉冲气动载荷，同时对桨叶结构载荷以及桨毂载荷都带来严峻的影响。

旋翼转速降低会导致桨叶频率比增加，所以桨叶通常设计成刚硬轻质，以提高挥舞摆振固有频率，尽可能的使其在转速区间内出现较少的共振点。马里兰大学研究团队针对变转速技术进行多个转速下的风洞试验[12]，试验中前进比最高达到1.2。试验表明：前进比增加，挥舞载荷4/rev的谐波量显著增加(4片桨叶)，同时桨毂垂直力4/rev的谐波量显著增加，且扭矩会更早的受到尾迹干扰的影响。桨盘低马赫数区和反流区扩大后，桨根气动力矩在旋转周期内会产生很强的峰值变化。在转速范围内，桨叶固有频率与旋翼整数倍转速频率存在多个交叉点，会带来严重的振动载荷问题。国内有关变转速动力学方面的研究较少，韩东等[13-14]针对变转速旋翼动力学问题进行理论分析和模型旋翼实验，研究发现：转速降低，挥舞、摆振低阶载荷幅值增加，且在共振转速状态下挥舞、摆振运动存在相互耦合，出现低阶挥舞、摆振载荷突增的现象。目前国内并未开展大前进比旋翼气弹动力学相关的研究工作。

降低转速会出现复杂的大前进比旋翼气弹动力学问题，对变转速旋翼设计提出了严格的要求。本文针对大前进比变旋翼气弹动力学问题，建立考虑大前进比配平的旋翼气弹分析模型；并对大前进比反流区气动力计算和配平计算进行适当修正，重点分析不同转速状态下的桨叶气动和结构载荷，并得出相应结论，为变转速旋翼结构设计以及后续的动力学优化设计提供理论依据。

1 大前进比旋翼气弹动力学建模

1.1 旋翼动力学模型

本文采用Green应变以及中等变形理论，通过Hamilton原理建立旋翼动力学方程

(1)

式中， δU为系统应变能，其变分形式可表示为

(2)

式中：ε为应变矩阵；σ为材料应力矩阵。

δT为动能项，表达式为

(3)

式中：qb为广义自由度矩阵；Mb为桨叶惯性运动引起的质量矩阵；FM为动能的非线性广义力。

δW为外载荷做功项，包括气动力和力矩两部分

(4)

式中：Fa为气动力；Ma为气动力矩；Gb为广义力系数矩阵。

采用中等变形梁理论以及有限元方法建立旋翼动力学模型，并采用Newmark积分法建立气弹响应计算模型，通过计算得到桨叶上每个自由度节点的响应，进而求解桨叶剖面结构载荷。桨叶剖面结构载荷是由当前剖面至桨尖的长度内单位长度气动载荷和剖面单位长度惯性载荷积分而来，为

F=FI+FA

(5)

式中：F为广义力； 下标I为惯性载荷部分； 下标A为气动载荷部分。桨叶载荷计算方法采用力积分法，表达式为

(6)

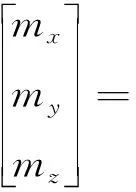
(7)

式中：L,M为剖面位置的三个力以及三个力矩，包括气动和结构载荷两个部分；f,m为整片桨叶的载荷量； 下标u,v,w分别为径向、弦向和垂直于弦向方向的位移。

1.2 大前进比反流区气动力计算修正

本文采用的旋翼气动力计算模型为非线性准定常气动模型。有效迎角采用小角度假设(见式(8))。但桨根段剖面ut速度小，有效迎角大，若继续采用小角度假设会造成较大误差；同时反流区桨叶剖面来流从翼型后缘向前缘移动，又处于负迎角状态。为准确描述在桨叶剖面坐标系内合速度矢量方向变化导致的实际迎角变化，对有效迎角表达式进行修正，修正后的表达式为

α=tan(-up/ut)≈-up/ut

(8)

式中：ut为剖面弦向速度；up为垂直于弦向速度。

(9)

XH-59A旋翼在μ=0.45的桨叶剖面迎角分布图，如图1所示。明显看出在未修正前剖面有效迎角在270°附近阶跃式跳动且不是连续分布，偏离真实情况。说明此时小角度假设在低马赫数区域以及反流区内不适用。通过修正方法改进之后，有效迎角呈连续变化且变化趋势合理(在后行侧低马赫数区域迎角为负)，这说明本文提出的方法有效可靠。

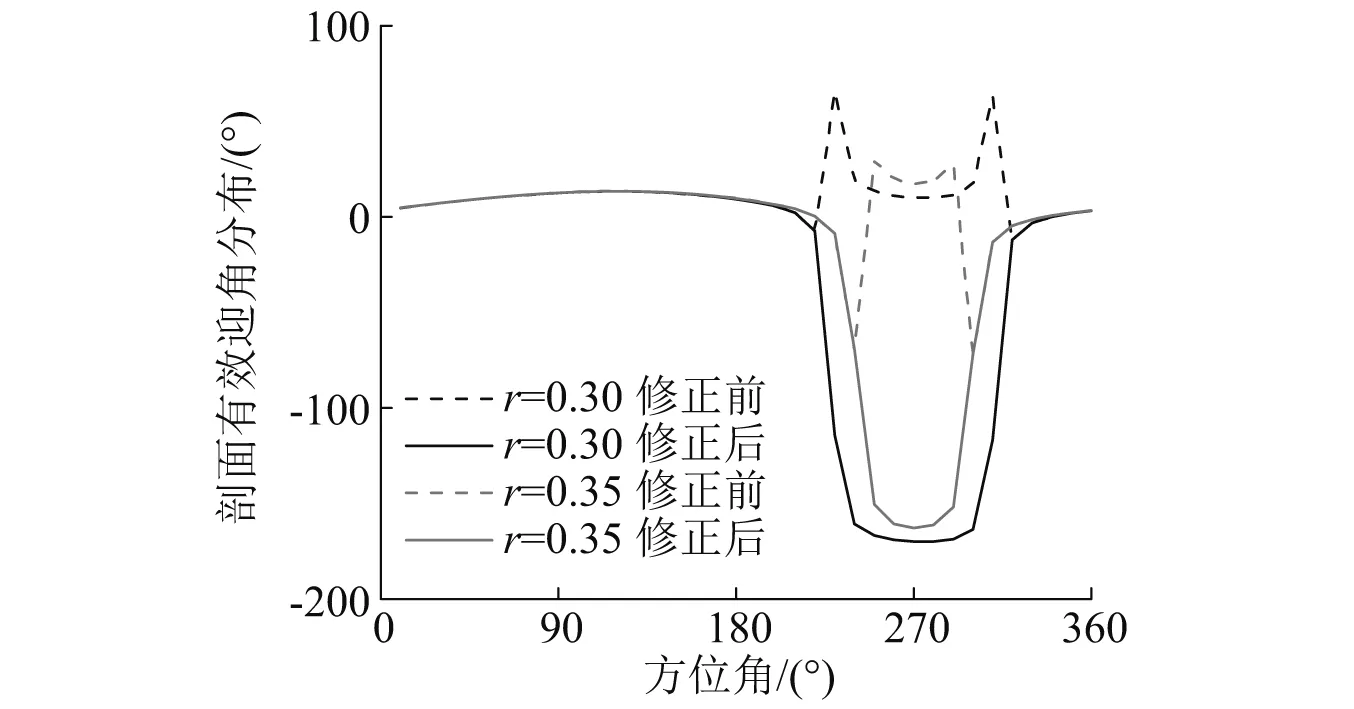
图1 迎角修正Fig.1 The correction of angle of attack

1.3 大前进旋翼气弹配平计算修正

大前进比旋翼气弹分析中配平计算为关键环节之一。目前旋翼配平计算普遍采用Newton迭代法，传统方法在中小前进比条件下具有很好的收敛性，但配平计算中只生成一次Jacobian矩阵，且矩阵质量与初始配平操纵有关。

随着前进比增加、气流非对称性增加、操纵量的变化对配平影响的敏感度增加，造成迭代计算量增加，配平计算难以收敛甚至发散。本文建立一种自适应Newton迭代过程，如图2所示。通过在迭代过程中判断残差数值变化情况，及时根据中间迭代的操纵值更新Jacobian矩阵，进行新一轮的配平迭代，采用逐步逼近的方式控制残差变化，从而能保持良好的收敛性，扩展配平计算的适用范围。

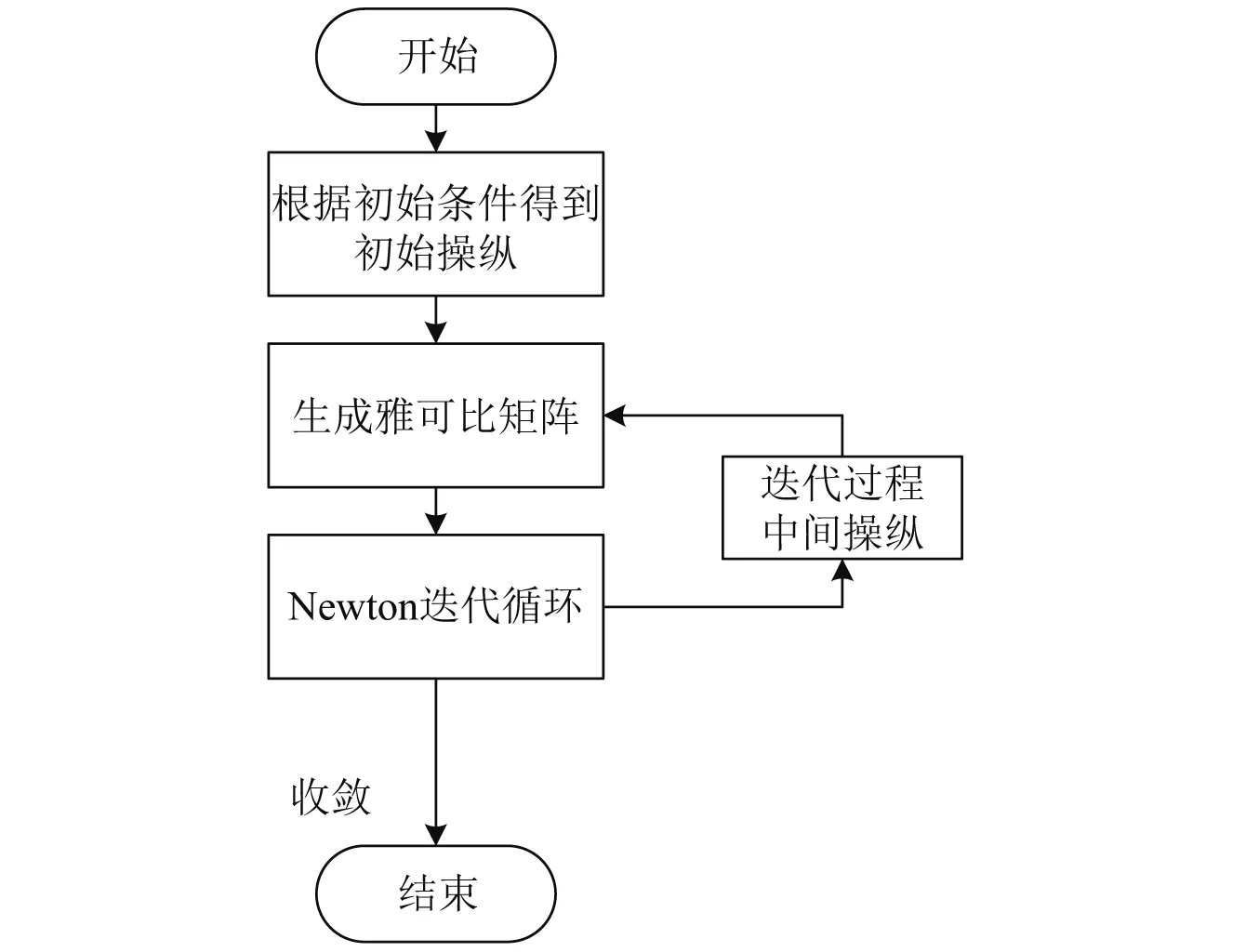
图2 Newton迭代流程Fig.2 Newton iteration flow

1.4 模型验证

为验证本文旋翼动力学模型的准确性，本节采用XH-59A全尺寸风洞试验计算的刚性桨叶模态频率并对比验证。具体参数可在文献[15]中查阅。本文计算的低阶桨叶模态与试验值吻合度良好，如图3所示。图中：F1为挥舞1阶；F2为挥舞2阶；E1为摆振1阶；E2为摆振2阶；T1为扭转1阶。证明本文采用的旋翼动力学模型准确有效。

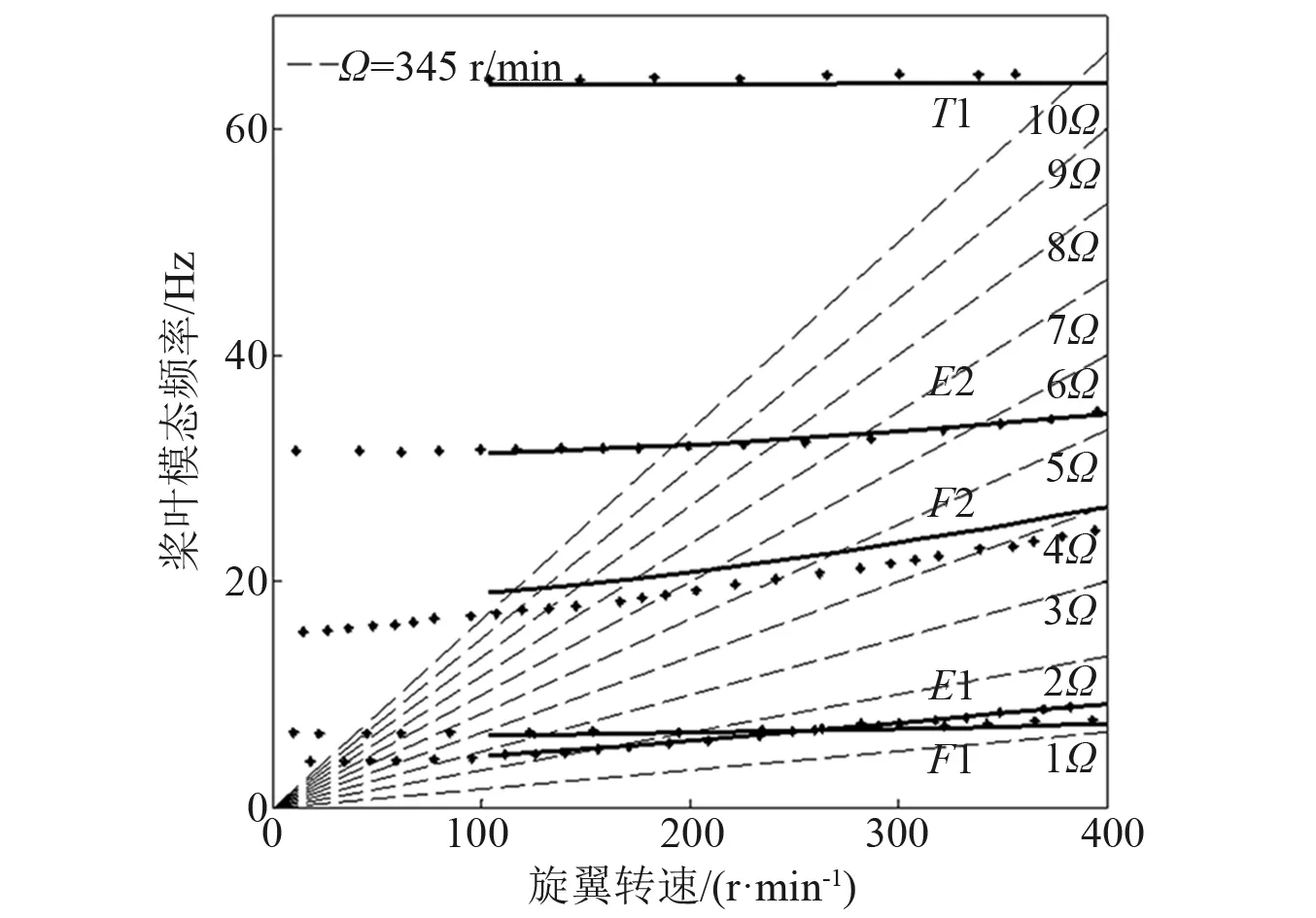
图3 桨叶模态频率Fig.3 Rotor blade dynamic modes

2 大前进比旋翼气弹动力学特性分析

本文采用的OSR专利技术中有较详细参数的旋翼作为算例模型，其采用NACA0012翼型，具体参数如表1所示。重点研究不同转速和前进比下的旋翼气动/动力学变化。选取75%～100%转速和3组前飞速度组合，如表2所示。包括桨叶模态的计算和单旋翼风洞配平的计算。

表1 OSR旋翼参数Tab.1 Rotor parameter of OSR

2.1 桨叶气动载荷分析

0.25R桨叶剖面气动力计算结果图，如图4所示。随着转速变化的曲线，从法向气动力结果图4中可知，由于转速降低，为保持相同拉力水平前行侧的升力增加以及后行侧升力集中，造成大前进比下桨根剖面法向力沿方位角分布出现较大波峰效果，产生周期性交变脉冲效应。转速越低，该现象就越明显。并且从图4中观察到，150 km/h前飞速度下桨根在后行侧区域法向力几乎为0，前飞速度增加开始出现负法向力，即会产生负升力效应。

图4 半径0.25R剖面法向力Fig.4 Normal force of 0.25R

半径0.25R剖面力矩计算值结果图，如图5所示。图5(a)中75%转速下力矩在270°附近出现脉冲式跳动(此时前进比为0.295)。图5(b)中，随着前飞速度增加至200 km/h，力矩峰值更加明显，脉冲式效应更突出。最终大前进比下桨根剖面产生周期性交变脉冲式气动力矩。旋翼后行侧的升力集中和反流区的交变脉冲效应都会对载荷造成影响。

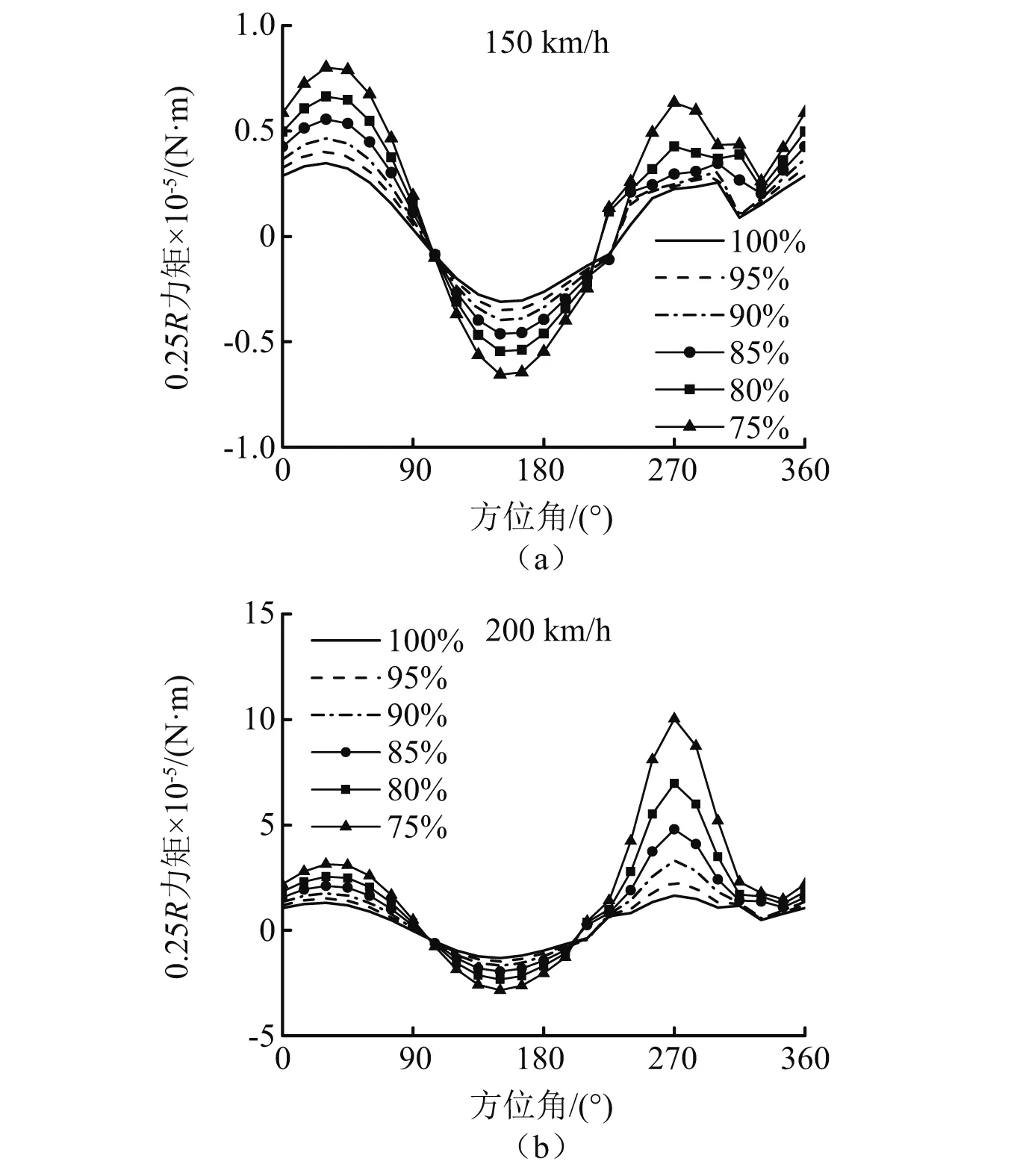
图5 半径0.25R剖面气动力矩Fig.5 Aero moment force of 0.25R

2.2 桨叶结构载荷分析

桨叶模态频率的计算如图6所示。从图6可知，在75%～100%转速区间，挥舞和摆振一阶频率未与转速整数倍频率发生交叉，这是为了避开共振问题，旋翼采用刚性桨叶将摆振1阶频率设置在1Ω以上。但挥舞2阶在转速区间内与5Ω频率发生交叉(旋翼为4片桨叶)，而5Ω频率的载荷会传递至机身带来振动问题，同时也说明变转速旋翼仍然存在共振问题，不容忽视。

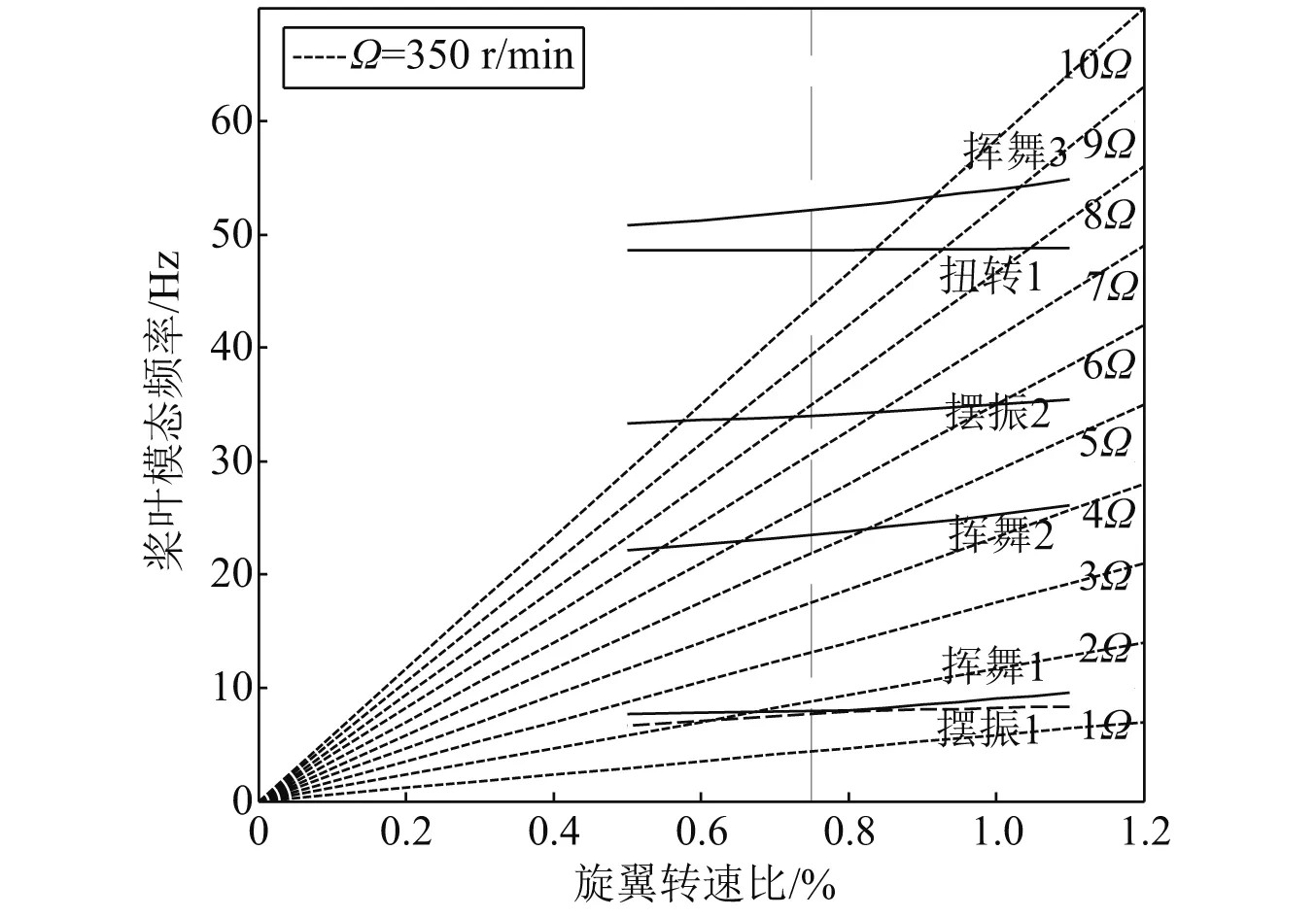
图6 桨叶模态频率Fig.6 Rotor blade dynamic modes

旋翼在大前进比下，剖面升力和力矩出现周期性脉冲效应，同时转速降低使得离心力刚度降低，造成挥舞载荷增大。计算桨根0.1R处挥舞和摆振弯矩并进行谐波提取。在200 km/h速度下，挥舞弯矩呈现多个波峰，整体载荷水平随转速降低而不断增加，载荷在270°附近波峰峰值明显增加，曲线逐渐呈现2阶谐波特征，说明挥舞2阶谐波分量占比增加，如图7(a)所示。图7(b)挥舞谐波载荷分解图也验证这一说法。转速降低，挥舞0阶、2阶、3阶载荷逐渐增加，而1阶谐波量降低。这是因为离心力刚度降低而总拉力不变，导致挥舞弯矩整体增加。而在配平计算中，随这转速降低，桨盘前倾角(αs)降低，导致1阶谐波量降低。

图7 桨根挥舞弯矩Fig.7 Flap bending moment of blade root

摆振弯矩计算结果图，如图8(a)所示。摆振运动受挥舞运动影响较大，受到气动力及摆振阻尼等影响。转速降低，挥舞弯矩在90°和270°附近数值增加，相应的摆振弯矩结果在90°和270°附近也出现较大波峰，且后行侧升力集中以及反流区负升力对摆振载荷影响更加明显。将摆振弯矩结果进行谐波分解并提取前3阶谐波，如图8(b)所示。随着转速降低或前飞速度增加都会造成摆振各阶谐波量增加，尤其对2阶、3阶载荷的影响最为显著。

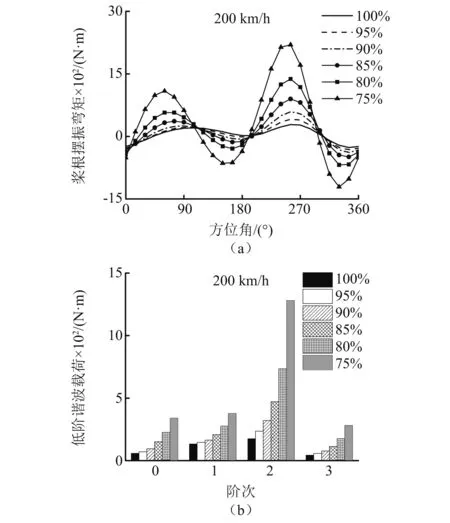
图8 桨根摆振弯矩Fig.8 Edge bending moment of blade root

注意到挥舞和摆振弯矩2阶谐波量在75%转速时增幅较大，尤其是摆振弯矩，这一点可以从图6模态频率图中观察到：在75%旋翼转速下挥舞模态接近2Ω频率，存在共振问题，摆振模态并未接近2Ω频率，但挥舞也引起摆振载荷的增加，且2阶影响显著，若继续降低转速必然会引起强烈的2阶摆振载荷，造成严重的动力学问题。

2.3 脉冲气动力对结构载荷的影响分析

为进一步研究大前进比状态下的周期性交变脉冲气动力对结构载荷的影响，计算85%转速不同前进比下的桨根0.1R剖面挥舞弯矩和挥舞弯矩中气动载荷部分(见式(7))，如图9、图10所示。从图中看出随着前进比增加，挥舞弯矩中的气动部分出现多波峰。随着前进比增加，反流区扩大即负升力区域增加，此时需要桨盘其他区域产生更多升力以抵消负升力，同时为满足升力对称性，后行侧升力集中在桨叶外段，气动力造成的挥舞弯矩进而增加。图9中270°方位角后挥舞弯矩显著增加也能验证这一点。

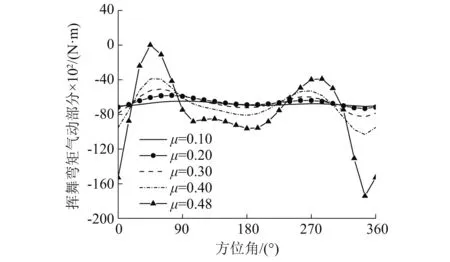
图9 结构载荷中气动载荷部分Fig 9 Part of airloads in structure loads

图10 挥舞弯矩Fig.10 Flap bending moment

3 结 论

为研究大前进比变转速旋翼气弹动力学特性，本文修正大前进比旋翼气动力计算方法和旋翼配平计算方法，建立了适用于大前进比旋翼气弹分析的模型，研究分析了不同转速和速度下旋翼气动力和结构载荷特性，并得到以下结论：

(1) 随着前进比增加，桨盘后行侧出现升力集中，同时大反流区内桨叶剖面几乎不产生升力甚至出现负升力，气动力矩在大反流区内出现较大波峰,升力及力矩呈现周期性脉冲效应。

(2) 周期性脉冲气动力引起挥舞弯矩中气动力部分的增加，脉冲式气动力的影响随着前进比的增加更加显著。

(3) 前进比增加，导致挥舞、摆振载荷增加，2阶挥舞、摆振载荷增加明显，且在转速区间内容易出现共振问题，恶化振动载荷结果。