Intelligent Fast Cell Association Scheme Based on Deep Q-Learning in Ultra-Dense Cellular Networks

Jinhua Pan,Lusheng Wang,Hai Lin,Zhiheng Zha,Caihong Kai

1 Key Laboratory of Knowledge Engineering with Big Data,Ministry of Education.School of Computer Science and Information Engineering,Hefei University of Technology,Hefei 230601,China

2 Anhui Province Key Laboratory of Industry Safety and Emergency Technology,Hefei 230601,China

3 Key Laboratory of Aerospace Information Security and Trusted Computing,Ministry of Education.School of Cyber Science and Engineering,Wuhan University,Wuhan 430072,China

Abstract:To support dramatically increased traffic loads,communication networks become ultra-dense.Traditional cell association (CA) schemes are timeconsuming,forcing researchers to seek fast schemes.This paper proposes a deep Q-learning based scheme,whose main idea is to train a deep neural network(DNN)to calculate the Q values of all the state-action pairs and the cell holding the maximum Q value is associated.In the training stage,the intelligent agent continuously generates samples through the trial-anderror method to train the DNN until convergence.In the application stage,state vectors of all the users are inputted to the trained DNN to quickly obtain a satisfied CA result of a scenario with the same BS locations and user distribution.Simulations demonstrate that the proposed scheme provides satisfied CA results in a computational time several orders of magnitudes shorter than traditional schemes.Meanwhile,performance metrics,such as capacity and fairness,can be guaranteed.

Keywords:ultra-dense cellular networks (UDCN);cell association (CA);deep Q-learning;proportional fairness;Q-learning

I.INTRODUCTION

With the fast development of mobile Internet and the increment of the number of user equipments (UEs),traffic loads in cellular networks dramatically increase,challenging the capacity of traditional cellular networks.The low-power femtocells densely deployed indoor or on hotspots are inexpensive but capable of supporting a large amount of traffic loads,which is widely considered as a promising technique for future ultra-dense cellular networks(UDCN)[1–3].In such a network,each UE may be covered by several overlapped femtocells,so cell association (CA) for each UE with the most appropriate cell becomes a critical issue for balancing traffic loads among the cells during the network optimization procedure [4].Traditional homogeneous cellular networks contain only a single type of cells,so the base station (BS) with the maximum signal-to-interference-plus-noise ratio(SINR) for each UE is usually associated [5,6].BSs in a heterogeneous network may have quite different transmission power and bandwidth setups,so the idea used for a traditional network may not achieve the optimal CA result anymore.For load balancing purpose,a basic idea is cell range expansion(CRE)which adds a bias on the receiving power values of the femtocells to attract more UEs to them [7].A Q-learning based scheme was proposed to obtain each cell’s bias value so that user requirements are satisfied and the overall quality of service(QoS)is optimized[8].

More general ideas are to optimize directly the associations between UEs and BSs.Yeet al.[9]maximized a logarithmic objective function by transferring it into a convex optimization problem through relaxation constraints and obtained the optimal CA result by solving its Lagrange duality.By modeling CA into a bipartite graph matching problem,a virtual BS method was used to keep the numbers of BSs and UEs equaling each other and an iterative Hungarian algorithm procedure was applied in [10].Iterations continued after removing the UEs associating with real BSs and the same number of virtual BSs,until all the UEs were associated with real BSs.It was pointed out in [11]that,when the objective function is proportional fairness,CA could be transferred into a twodimensional assignment problem by virtualizing each BS into an amount of virtual BSs.Hungarian algorithm was used to solve this assignment but the time cost determined by the total amount of virtual BSs becomes quite large.A dynamic clustering model was used in [12]for CA,a matching game within each cluster was performed and the final matching result was obtained.Zhouet al.[13]studied the CA problem in femtocell networks toward the minimization of service latency.Several near-optimal algorithms were proposed including a sequential fixing algorithm,a rounding approximation algorithm,a greedy approximation algorithm,and a randomized algorithm.Sunet al.[14]aimed at maximizing the system’s long term throughput and modeled CA as a stochastic optimization problem.A restless multi-armed bandit model was used to derive an association priority index and an index-enabled association policy was raised for making CA decisions.

A generic cell association problem is NP-hard,the above schemes may find the optimal performance in terms of a certain metric,but their computational time costs are too large.Intelligent methods could learn,predict,and make decisions based on vast training,so it provides a possibility to design a new type of CA schemes.To maximize the long-term service rate and minimize its variance,Liet al.[15]raised a distributed reinforcement learning scheme to solve the load balancing problem during associations between vehicles and BSs in the dynamic vehicular network scenario.To solve the joint optimization on CA and power allocation,a multi-agent Q-learning scheme was proposed in [16].However,Q-learning based scheme may not traverse enough state-action pairs when the solution space is quite large,so it may become a trend to combine reinforcement learning with deep neural network (DNN) for similar decisions.Zhonget al.[17]modeled the multichannel access problem into an observable Markov decision process and raised a deep reinforcement learning based scheme to maximize the average channel quality of each user in a certain period.Zhaoet al.[18].designed a distributed multi-agent deep reinforcement learning scheme for the joint CA and resource allocation optimization.A double deep Q network was used to maximize network utility under the premise of guaranteeing QoS.Mean field theory was used to model the CA problem in[19]and a deep Q-learning based scheme was proposed to focus on the case when each user may not observe all the states in the system.In[20],the CA problem between vehicles and BSs in V2X communication was modeled as a discrete nonconvex optimization and a distributed deep reinforcement learning scheme was proposed.

The above works are representative optimization solutions for the CA problem,but for the application in a UDCN,it is difficult to find a scheme that completes the CA optimization in a sufficiently small computational time.This paper proposed a deep Q-learning based CA scheme to maximize the network utility.Qlearning is used to update the Q values of state-action pairs and generate samples to train the DNN toward convergence.The trained DNN is a fitting of the Q function to predict the Q values of actions in the scenarios with BSs at the same locations and UEs with the same distribution.To apply the trained DNN,the state of each UE is inputted and the BS corresponding to the action with the maximum Q value is associated.Considering proportional fairness as the network utility,simulations compared with several traditional schemes demonstrate that the proposed scheme achieves almost the highest proportional fairness and very high Jain’s fairness in an extremely low computational time.

The remaining of this paper is organized as follows.In Section II,the problem is modeled as a combinatorial optimization.Section III proposes our deep Qlearning based CA scheme.Section IV shows the convergence of the proposed scheme and compares it with several representative schemes.In the end,Section V concludes the paper.

II.SYSTEM MODEL

Considering a UDCN composed of macrocells and femtocells whose BSs are denoted by B={Ba|a=1,2,...,N},whereNis the total number of BSs.All the BSs operate in the same frequency bandW.UEs in the network coverage area is denoted by U={Us|s=1,2,...,M},whereMis the number of UEs in the scenario.A 0/1 variablexsais used to represent the association betweenUsandBa,i.e.,1 if associated and 0 otherwise.The number of UEs associated withBacan be denoted bySupposing that these UEs averagely divide the whole bandwidth ofBa,the rate for the association betweenBaandUsis

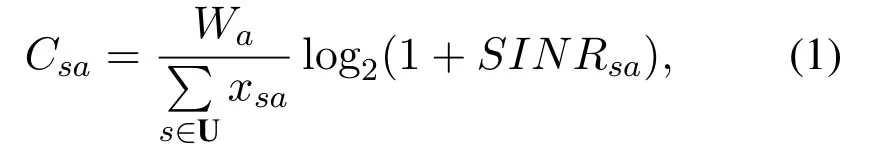
AndSINRsais calculated by

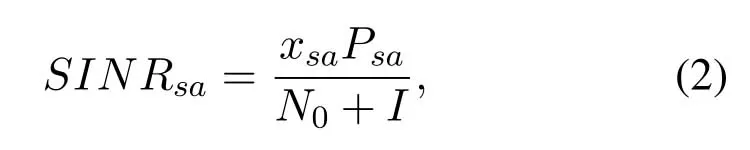
whereN0is the power of additive white Gaussian noise (AWGN),represents the total interference,Psarepresents the receiving power of the link betweenUsandBa.The association result x is anM ·Nmatrix,composed ofxsa,so the maximization of the total utility is written as

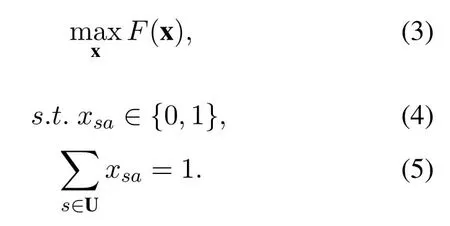
If capacity is the objective,we haveF(x)=Similarly if proportional fairness is the objective,System capacity is a performance metric with well-known physical meaning,so it is quite common to use it as the objective of resource management.However,this objective function may lead to the allocation of most resources to only a few UEs near the BSs,which sacrifices the other UEs.Therefore,we tend to use proportional fairness as the objective function so that a tradeoff between system capacity and UE fairness is reached.

III.DESIGN OF THE PROPOSED SCHEME

Since the above combinatorial optimization requires too much computational time in UDCN,this paper devotes to designing a fast CA scheme that may reach a near-optimal association of the above problem.We firstly try a Q-learning based CA scheme,which converges to the optimum by a continuous search integrating a reward and punishment mechanism.It focuses on the strategy toward the global optimum but the time cost becomes unacceptably large because the dimensions of state and action spaces are large in UDCN.Deep Q-learning uses a well-trained DNN to take the place of the Q table,which may drastically decrease the time cost on the premise of guaranteeing a quite competitive utility.Therefore,we apply it into the CA problem and propose a deep Q-learning based scheme in this Section.

3.1 Q-learning Based CA Scheme

Q-learning is a classic model-independent reinforcement learning algorithm,whose intelligent agent learns from states’ optimal actions toward the maximization of the cumulative expectation through a target-oriented learning process[21].Entities involved in this process are listed as follows.

Environment:the scenario including macrocells,femtocells,UEs,buildings,terrain,etc.

Agent:the decision-maker that changes the association of a certain UE during each iteration.

State:a state is a UE,and all the UEs in the scenario form the whole state space.

Action:an action is a decision made by the intelligent agent,so it is an association with a BS in this issue,or denoted directly by a BS.The UE may associate with another BS or it may not associate with any BS before an action is chosen.All the BSs in the scenario form the whole action space.

Reward:the variation of the total utilities before and after an action.Denoting the associations before and after an action as xt−1and xt,the reward can be calculated as

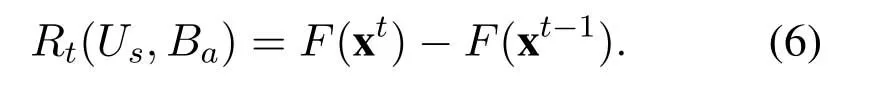
Q table:a two-dimensional table storing Q values of all the state-action pairs.Each row corresponds to a state,and each column corresponds to an action.

Bellman equation:the equation to iteratively update the Q value,given by

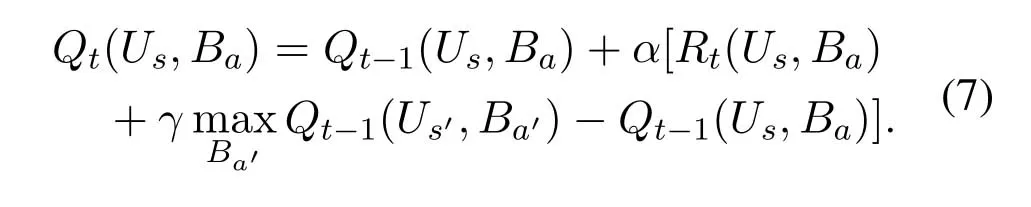
whereγ ∈[0,1]is the discount factor indicating the impact of future reward on the current decision.α ∈[0,1)is the learning rate which decides the retainment of the experience and affects the convergence rate.Ba′represents the action forUs′reaching the maximum Q value.

Improvedє −greedyaction selection strategy:traditional strategy is to select equivalently a random action with probabilityєand to select the action reaching the maximum Q value with probability 1−є.In the CA issue,UEs tend to associate with a BS not far from them,so it is reasonable that the selection probabilities must be related to the distances between UEs and BSs.In our improved strategy,before episode reaches a given bound,the selection probability of each actionBais whered(Us,Ba) represents the distance betweenUsandBa.Note that,distances in (6) may also be replaced by a function of received signal strength which could be easily detected in a real network.Afterepisodereaches a given bound,the above strategy is used with probabilityє,otherwise the action maximizing the Q value is selected.

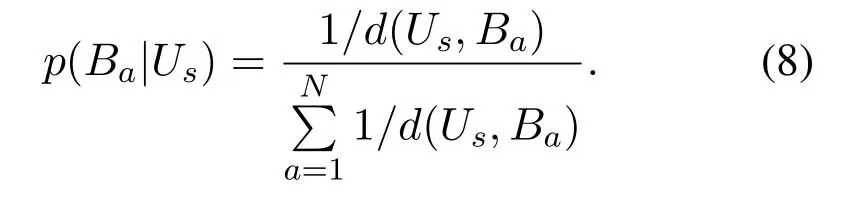
The main idea of a Q-learning based CA scheme is to calculate the reward during each iteration and use it to update the Q value of the corresponding state-action pair.After the Q table converges,each state selects the action that maximizes its Q value.The procedure of algorithm 1 is shown below.

3.2 Deep Q-learning Based CA Scheme

?

The Q-learning based scheme in the above subsection can reach a near-optimal solution,but a single Q table may not be used for different scenarios and the scheme should run again when the scenario is changed.Combining with the forecasting capability of DNN in the scheme,we could use a training process to keep on updating the DNN,so that the relationship between stateaction pairs and their Q values could be used to predict the utility of each UE-BS pair in a scenario with the same BS locations and UE distribution.Settings and parameters in this scheme are almost the same as those in the Q-learning based scheme,except that the state ofUsinputted into the DNN should be represented by its receiving power values from all the BSs,given by ps={psa|a=1,2,...,N}.

The convergence of a DNN is substantially reached by updating its weights and bias terms.The converged DNN should be a fitting of the Q function,and the experience replay strategy makes the fitting stable [22].In the designed deep Q-learning based CA scheme,thekth sample in the storage is denoted by,where Q(Us(k))={Qt(Us(k),Ba)|a=1,2,...N}represents the vector of Q values of all the actions of stateUs(k).The scheme contains the following two phases.

3.2.1 Training phase

The agent trains offline toward a converged DNN and a number of samples are randomly chosen from the storage during each training.The procedure is shown by Algorithm 2.

First of all,we initialize the DNN,the associations x,the Q table,and related parameters.Some parameters that are different from Algorithm 1 are the storage capacityT,the number of samples for each trainK,the number of observed samplesV,the training intervalS,and the maximum number of iterations forepisode.

Then,we choose a random state and carry out the same Q value update sub-process as Algorithm 1 to obtain a sample,including action selection strategy,next state selection,reward calculation,Q table update,etc.The sample will be put into the storage as long as there is still space.Once the amount of samples in the storage exceedsV,we extractKsamples from the storage to train the DNN.

The activation function of the neurons in the DNN is a sigmoid function,given byr=1/(1+e−z).Since its output range is(0,1),the Q value vectors should be rectified,i.e.,the values less than 0 are rectified to 0s.Then,the values are normalized to the range(0,1).

Generally speaking,a deeper network could decrease the number of neurons,which can further decrease the generalization error.However,a too deep network may cause a gradient vanishing problem,which may on the contrary increase the generalization error[23].Combining with our experience,the DNN used in the scheme contains five layers.The numbers of neurons in input,output,and hidden layers are all set to the same as the number of BSs,as shown by Figure1.

?

Once a state is inputted into the DNN,a vector is outputted,representing the Q values of all the actions.AfterKstates are inputted,the mean squared error(MSE)of their loss is calculated by

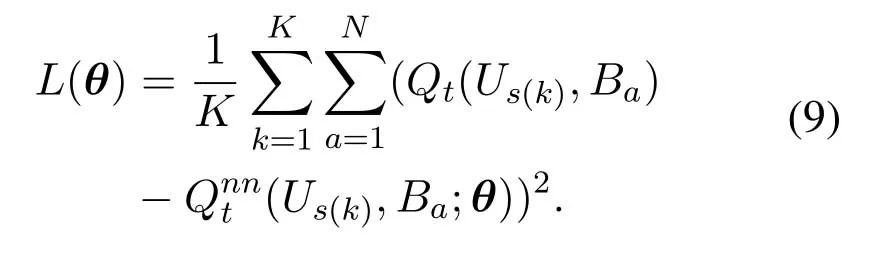
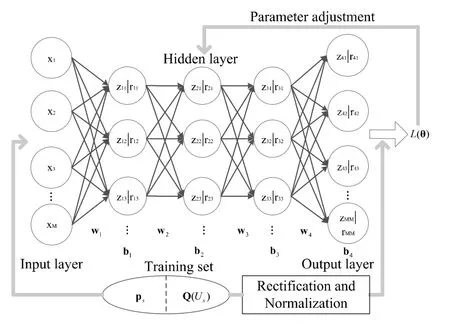
Figure1.Training of the DNN.

whereθ={w1,...,w4,b1,...,b4}denotes weights and bias terms.represents the Q value of a certain state-action pair obtained by the DNN.Eq.(9) actually shows the difference between the calculated Q value and the ideal Q value.Backpropagation is used to calculate the gradients of the loss on all the parameters,given by

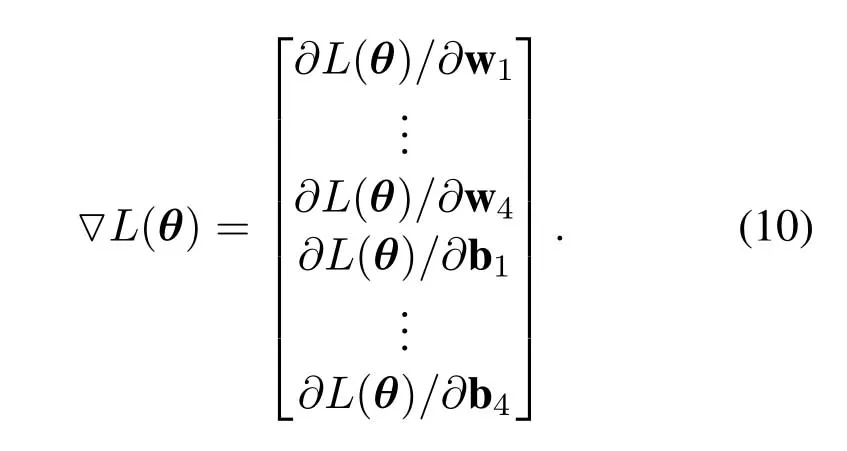
Then,the elastic gradient descent method is used to update the parameters,given by

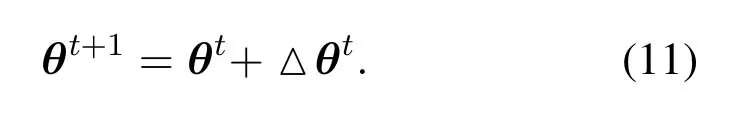
where △θtis generated by the descent method whose details are out of the scope of this proposal.

3.2.2 Application phase

By applying the trained DNN for CA decision,we could quickly reach a satisfied association result.Specifically,we just need to input the state of each UE into the DNN,so that the Q values of all the actions can be obtained and the one with the maximum Q value is selected.

Since the scheme provides the CA result in a quite short computational time,it is suitable for quite dynamic scenarios where UEs move rapidly without obviously changing their distribution.For such a scenario,traditional game or optimization based schemes take too much time to reach a satisfied CA result and the UEs already move to other locations and their channel conditions are already changed.However,the proposed scheme may provide real-time CA decisions whose performance can be always close to the optimum as time goes on.The procedure of the application phase is shown in Algorithm 3.

?

IV.PERFORMANCE EVALUATION

Simulations are performed in a square area with side length equaling 200 meters.The UDCN is composed of 30 BSs with 1 macrocell in the center and 29 femtocells located uniformly in the area.A number of UEs are distributed obeying the Poisson clustering process[24].Transmission powers and bandwidths are 40 dBm and 10 MHz for the macrocell and 21 dBm and 6 MHz for the femtocells.Spectral density of the AWGN is−174 dBm/Hz.Path loss is calculated by the close-in free space reference distance model with frequency-dependent path loss exponent [25],given by

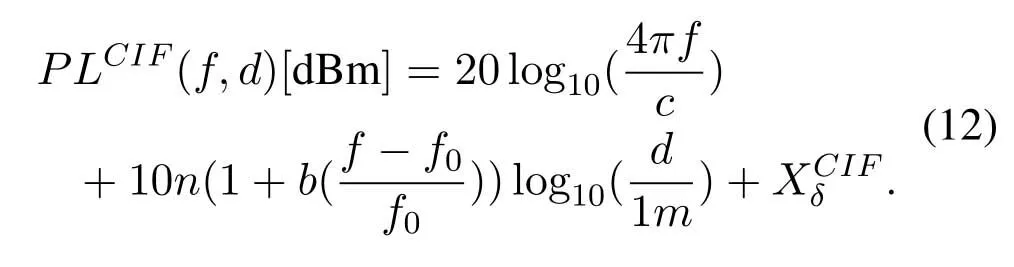
where the carrier frequency isf=3.5×109Hz,the path loss exponent isn=2.59,the slope optimization parameter isb=0.01,the shadowing fading isand the reference frequency isf0=39.5×109Hz.The following simulations are run on a computer with Intel Core i5-3570 CPU@3.4 GHz and 8 GB RAM.

4.1 Convergence of the Proposed Schemes

For the Q-learning-based scheme,referring to[21]and our experience,α,γ,andєare set to 0.4,0.9 and 0.4,respectively.By simulating the associations of 300 UEs,we show the convergence effects of the following four configurations:

Purely random:the initial associations of all the UEs are completely random.Entries in the Q table are all set to 0.The next state selection strategy is also random.The traditionalє −greedyaction selection strategy is applied.

Max-SINR Initiation:compared with the above configurations,the initial associations of all the UEs are changed into max-SINR based associations.Corresponding entries in the Q table are set to 0.4.

Max-SINR + Enhanced action selection:compared with the above configurations,the difference is that the improved action selection strategy in Subsection 3.1 is applied.

In fact, the more he considered the matter, the more he felt that he would be wise to put a good face on it, and to let people suppose that he had really brought about the marriage of his own free will

Algorithm 1:compared with the above configurations,the difference is that the next state selection strategy in Subsection 3.1.A is applied,so the configurations become totally the same as Algorithm 1.Considering the receiver sensibility as−79 dBm[26],we obtain the maximum transmission range of a femtocell BS as 83.2 meters which is configured as the selection range of the next action.

Figure2 shows the comparison of the four configurations.We can see that,after three improvements on the configurations,the proposed Algorithm 1 converges much faster than the others and it is the stablest among all of them.

For the deep Q-learning based scheme,referring to [23]and our experience,the parameters are set as follows:the maximum number of iterations is set to 50000,T=2000,V=2000,S=500 andK=400.Besides,the step length and decay in the gradient descend method are set to 0.05 and 0.5.Figure3 shows the convergence effects of Algorithm 2 and three other configurations as described above.We can see that the configuration in the proposed Algorithm 2 converges faster than the others.

Figure4 compares the association results of the two schemes in Section III.To demonstrate the relationship clearly,a scenario with 200 UEs are used.The figures show that the associations by the two schemes are almost the same,except for a few UEs locating far from all the BSs.For those UEs,the performances of associating with the most appropriate two or three BSs are quite similar,so the differences actually cause quite limited effect on the performance of the whole network.

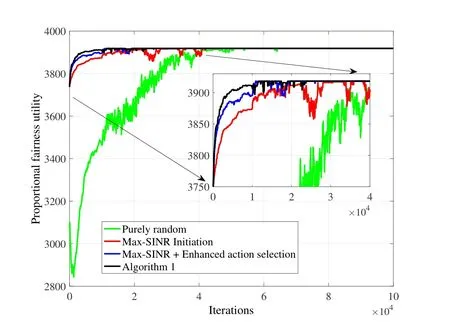
Figure2.Convergence of the Q-learning based CA scheme with different configurations.

4.2 Performance Comparison with Representative Schemes

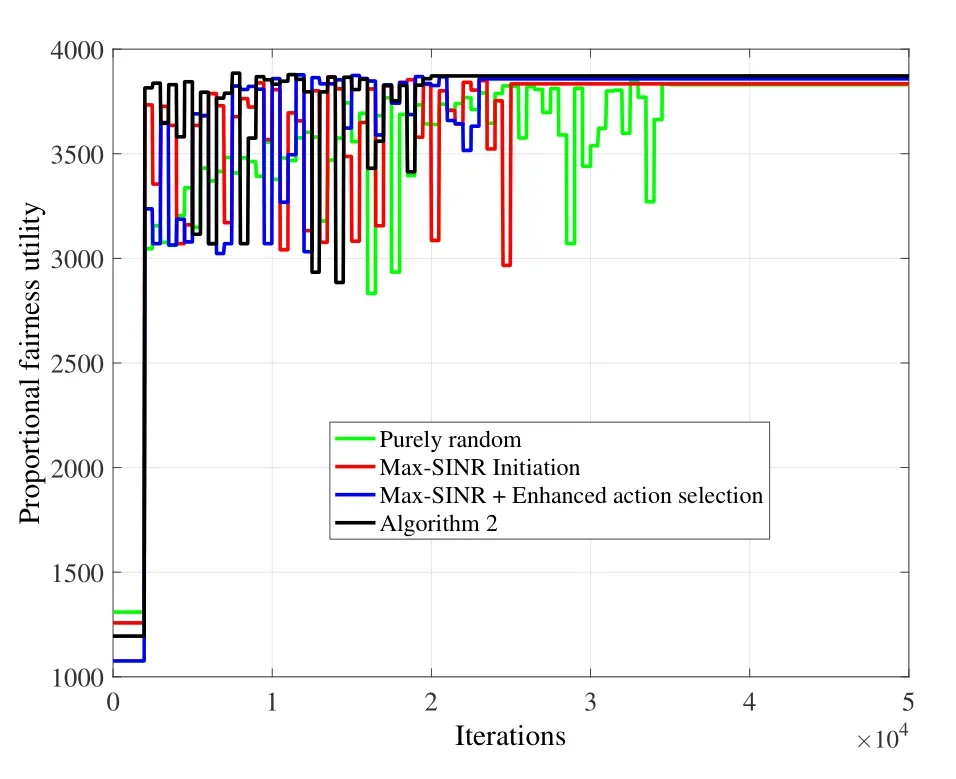
Figure3.Convergence of the deep Q-learning based CA scheme with various configurations.

In this subsection,we compare our proposals with several traditional schemes,including Hungarian algorithm based scheme toward maximum proportional fairness [11],max-SINR scheme [5],and Q-learning based scheme toward maximum CRE bias [8],and the curves are denoted by HA,SINR,and QLCRE,respectively.The optimization objectives of the proposed schemes are generic,so we draw four curves for them in the following figures,including Q-learning based scheme toward maximum capacity(QL-C),Q-learning based scheme toward maximum proportional fairness(QL-PF),deep Q-learning based scheme toward maximum capacity(DQL-C),and deep Q-learning based scheme toward maximum proportional fairness(DQL-PF).

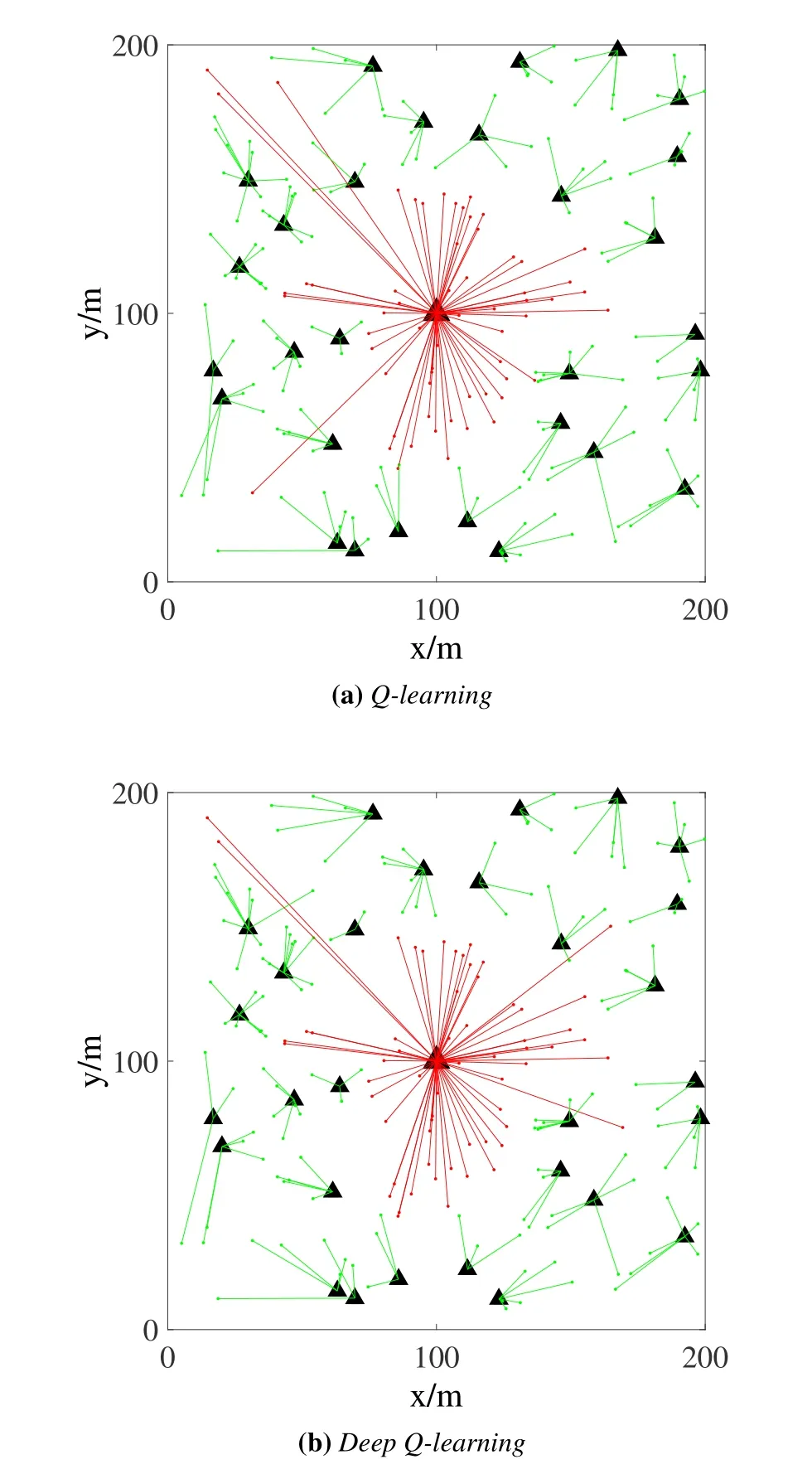
Figure4.Comparison of CA results.

Figure5 shows the computational times of all the above schemes.HA transforms the problem into a two-dimensional assignment problem and the solution is polynomial-time,but the complexity is as high asO[(MN)3]and its computational time is much longer than all the other schemes.We can only draw the left part of its curve,because its computational time becomes unacceptably long for an ordinary computer.The three schemes using Q-learning all require a search process,so their time costs are all relatively long.QL-PF requires only a fine adjustment from the initiation of max-SINR,while QL-C requires more adjustment during the search,so their computational times are a little bit different from each other.QL-CRE only searches on the CRE bias,which has a much smaller solution space than the common CA scheme,so it is generally the fastest among the three schemes using Q-learning.The schemes with the minimum computational times are the rests,i.e.,SINR,DQL-PF,and DQL-C,whose computational complexities are allO(MN).SINR requires an amount of division operations,while the two deep Q-learning based schemes require mainly additive and multiplicative operations,so the latter two schemes require even less time than the traditional max-SINR scheme.Note that,the counted running time of a deep Q-learning based scheme is on the application phase.Their training phase surely requires as long time as Q-learning based schemes or even longer,but that phase is not required for CA decisions after the DNN converges and the training is complete.The proposed deep Qlearning based CA scheme fits for mobile scenarios where UEs gradually move.Since the scheme requires a time cost in the magnitude of milliseconds for a scenario containing even more than 10000 UEs,it can be used to dynamically make CA decisions,as UEs could not move too much within a second.By contrast,schemes with severely large time costs cannot be used for mobile scenarios,because they may not complete the optimization before UEs move to new locations.In summary,among all the compared schemes,only the traditional max-SINR scheme and the two deep Qlearning based schemes are fast enough for practical usage in UDCN,i.e.,in the magnitude of milliseconds.It is a strong evidence to predict that,after the wide usage of received signal strength based,SINRbased,and capacity-based schemes in traditional networks,a quite promising type of schemes specifically for UDCN may be deep Q-learning based schemes.

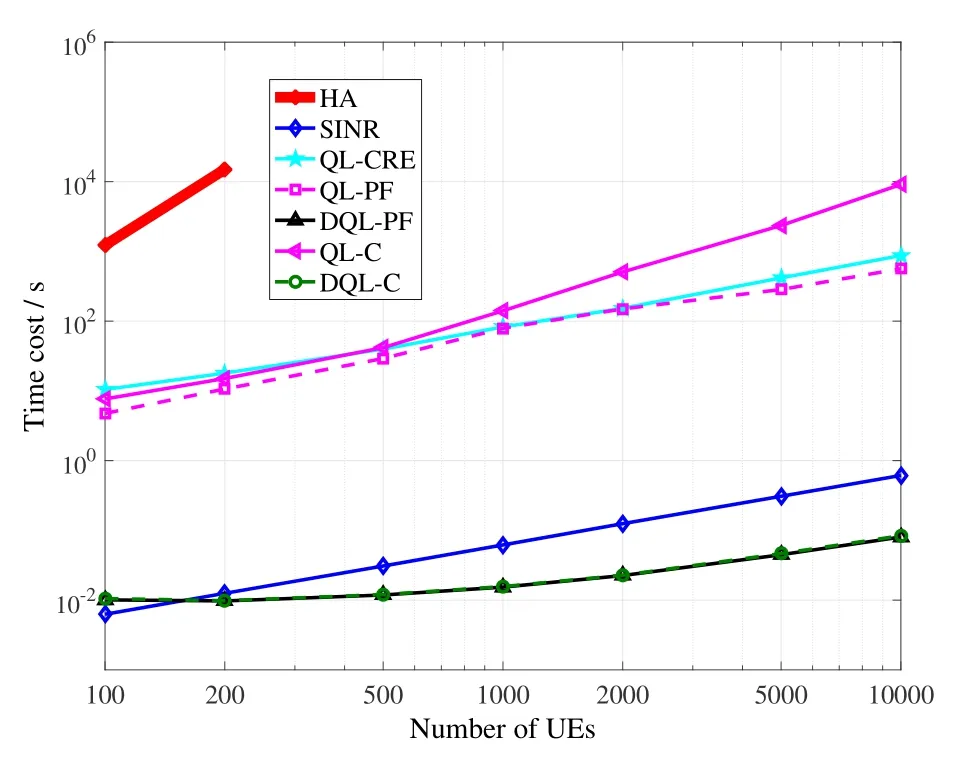
Figure5.Comparison of computational times.

Figure6,Figure7,and Figure8 further compare the above schemes,in terms of proportional fairness utility,Jain’s fairness,and system capacity.HA,QLCRE,QL-PF,and DQL-PF tend to improve proportional fairness,so these schemes achieve quite high proportional fairness,as well as relatively high Jain’s fairness.The Jain’s fairness of DQL-PF is a bit lower than the other three schemes due to the fact that its design and training of the DNN may still be improved.SINR is a traditional tradeoff scheme between fairness and system capacity,so its proportional fairness and Jain’s fairness are also high but lower than the four schemes above.In terms of system capacity,curves of QL-C and DQL-C are obviously much higher than the other schemes,because the two are specifically for optimizing this performance metric.Along with the increment of the number of UEs,system capacity should not always dramatically increase,because these UEs share the same total bandwidth.

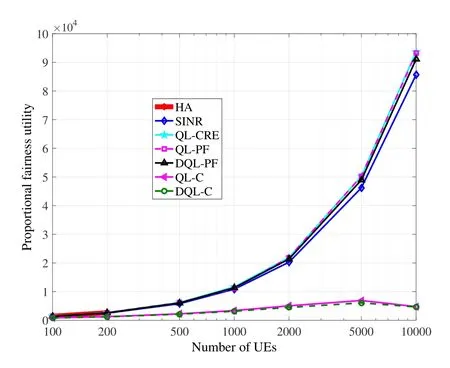
Figure6.Comparison of proportional fairness.

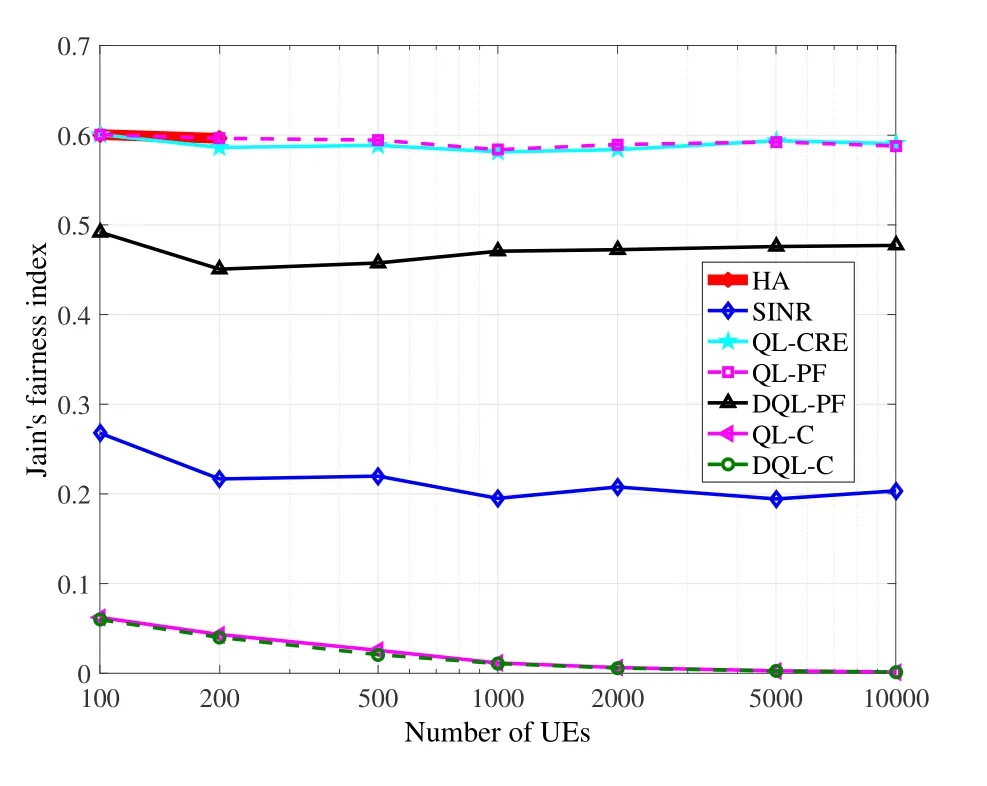
Figure7.Comparison of Jain’s fairness.

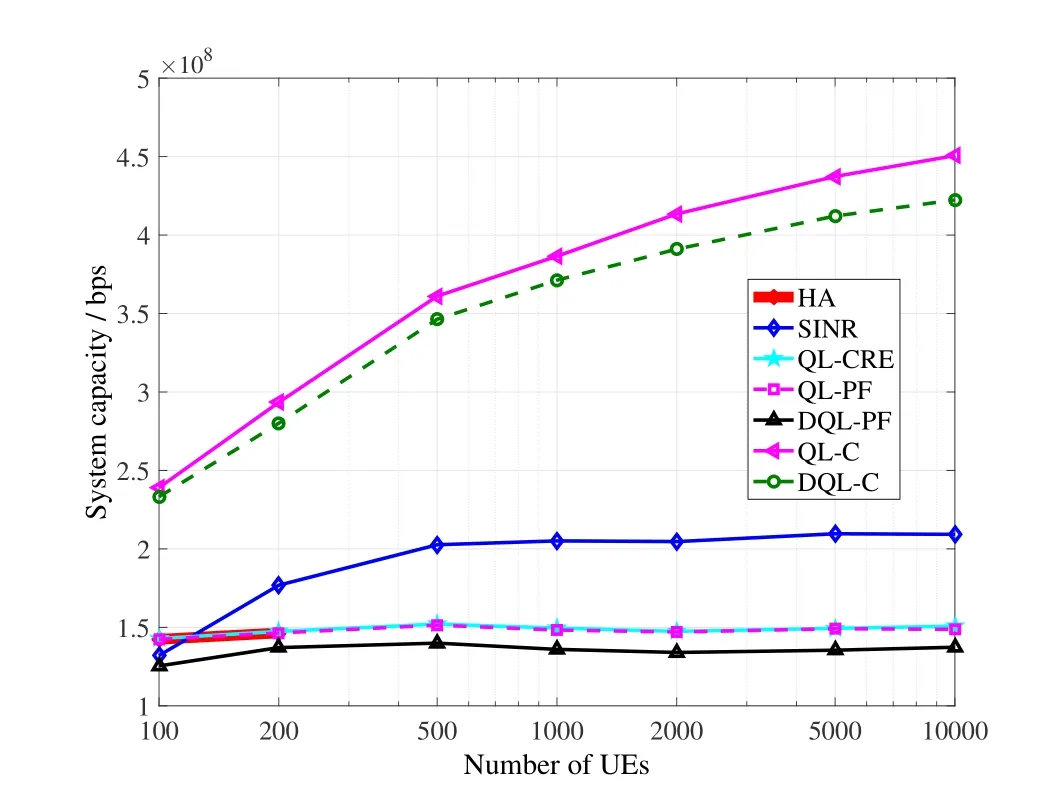
Figure8.Comparison of system capacity.

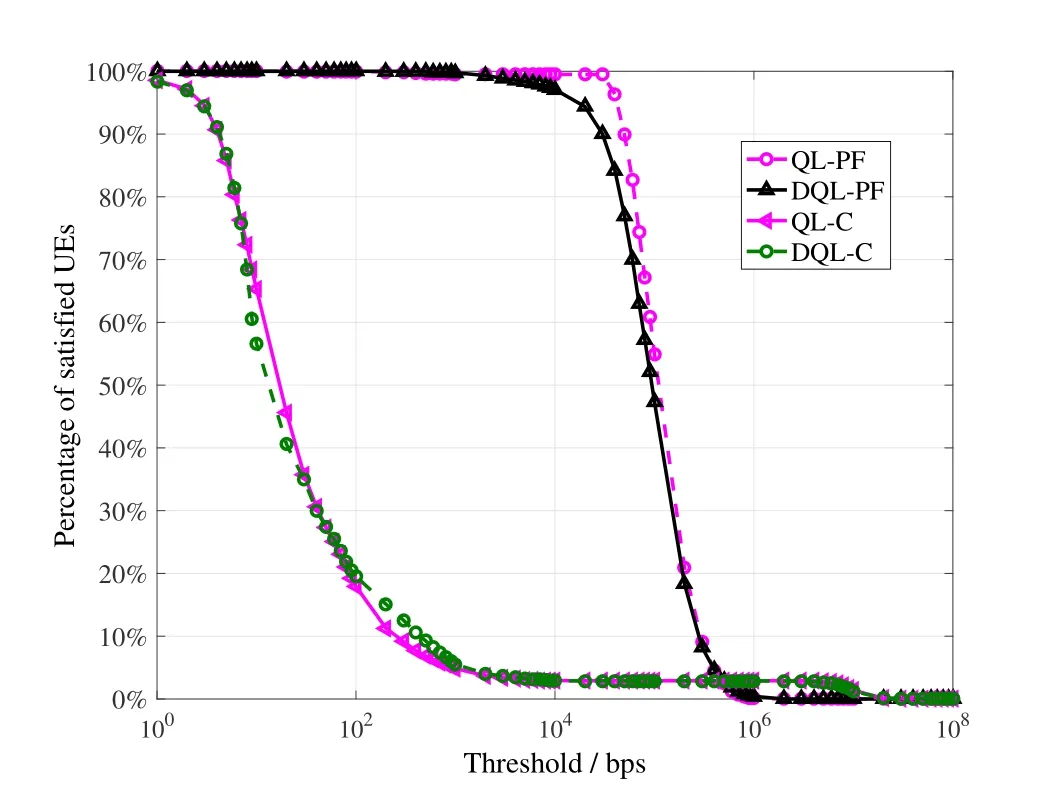
Figure9.Comparison of the percentages of satisfied UEs.

Although most of the schemes achieve much lower system capacity than QL-C and DQL-C,it should not be an evidence to propose the two schemes.By randomly deploying BSs and UEs in the simulation area,there are always a few UEs too close to some BSs,so a scheme maximizing the system capacity tends to provide these UEs an extremely good association condition,such as allocating each of them a whole BS.This kind of association strategy may reach a very high system capacity,but it may not be reasonable because of the sacrifice of too many other UEs.On the contrary,by maximizing proportional fairness,a scheme tends to balance the loads on some level,so the fairness is high and no UE is strategically sacrificed.To the best of our experience,the achieved system capacity by proportional fairness oriented schemes,such as QL-PF and DQL-PF,are stable,which demonstrates actually a normal association solution with most of the UEs basically satisfied.Take the scenario with 1000 UEs as an example,Figure9 shows the percentages of UEs whose achieved capacities surpass a given threshold.Most of the UEs in QL-PF and DQL-PF achieve capacities between 10 Kbps and 1 Mbps,while most of the UEs in QL-C and DQL-C achieve less than 100 bps.Given a relatively compromised threshold,such as 10 Kbps,the percentages of satisfied UEs by QLPF and DQL-PF reach more than 95%,but those of the other schemes reach only less than 5%.

V.CONCLUSION

UDCN is a major trend of future network development and CA becomes a significant research topic for such a network paradigm.An extremely fast CA scheme based on deep Q-learning was proposed in this paper.A DNN was trained iteratively until it converges using samples generated from the Q-learning process.The converged DNN was then applied for CA decisions in the scenarios with the same locations of BSs and the same distribution of UEs.Simulations demonstrated that the proposed scheme could make a CA decision in the magnitude of milliseconds,which is much faster than the compared traditional optimization schemes.Therefore,it should be a promising scheme for CA in UDCN scenarios.

ACKNOWLEDGEMENT

This work was supported by the Fundamental Research Funds for the Central Universities of China under grant no.PA2019GDQT0012,by National Natural Science Foundation of China (Grant No.61971176),and by the Applied Basic Research Program of Wuhan City,China,under grand 2017010201010117.