Development of Hybrid ARQ Protocol for the Quantum Communication System on Stabilizer Codes
Jiaxin Li,Zhongwen Guo,Hongyang Ma
1 College of Information Science and Engineering,Ocean University of China,Qingdao 266100,China
2 School of Science,Qingdao University of Technology,Qingdao 266033,China
Abstract:In this paper,we develop a novel hybrid automatic-repeat-request(ARQ)protocol for the quantum communication system using quantum stabilizer codes.The quantum information is encoded by stabilizer codes to against the channel noise.The twophoton entangled state is prepared for codeword secure transmission.Hybrid ARQ protocol rules the recognition and retransmission of error codewords.In this protocol,the property of quantum entangled state ensures the security of information,the theory of hybrid ARQ system improves the reliability of transmission,the theory of quantum stabilizer codes corrects the flipping errors of codewords.Finally,we verify the security and throughput efficiency of this protocol.
Keywords:quantum communication system;hybrid ARQ;quantum stabilizer codes;reliability;security.
I.INTRODUCTION
Quantum communication protocol enables users of quantum network to establish a shared secret communication to achieve message confidentiality and integrity,thus it plays an important role to achieve secure communications.There have been many protocols for quantum network proposed and their security has been extensively studied [1–9].In 1984,Bennettet al.[10]proposed a protocol (BB84) for quantum key distribution (QKD) in which the sender transmits single-photon pulses to the receiver in such a way that security is ensured by physical laws.In 1992,Bennett [11]showed that in principle any two nonorthogonal quantum states suffice the task of distributing secret information over an insecure channel and presented a simplified QKD protocol (B92).In 2004,Scaraniet al.[12]introduced a new class of QKD protocols,tailored to be robust against photon number splitting(PNS)attacks.This protocol is provably better than BB84 against PNS attacks at zero error.In 2012,Liuet al.[13]utilized the four-particleχ-type states as the information carriers,presented a quantum protocol for private comparison with the help of a semi-honest third party(TP).In 2013,Liet al.[14]proposed a quantum probabilistic encryption algorithm for a private-key encryption scheme based on conjugate coding of the qubit string,and analyzed the security of the schemes against two kinds of attacks.In 2017,Joyet al.[15]proposed two deterministic secure quantum communication (DSQC)protocols employing three-qubit GHZ-like states and five-qubit Brown states.In 2018,Wengerowskyet al.[16]presented an entanglement-based wavelengthmultiplexed quantum communication network,which is fully passive and thus has the potential for unprecedented quantum communication speeds.In 2019,Zhouet al.[17]put forward a semi-quantum key distribution(SQKD)protocol based on four-particle cluster states,which can achieve key distribution among one quantum party and two classical parties simultaneously.In 2019,Brassardet al.[18]proposed a noisy interactive quantum communication,studied the problem of simulating protocols in a quantum communication setting over noisy channels.In 2019,Cuiet al.[19]proposed a Measurement-device-independent QKD scheme using hyper-encoding,which is unconditionally secure,even for weak coherent pulses with decoy states.In 2019,Yanet al.[20]proposed a mutual semi-quantum key agreement protocol using Bell states,which not only resists against some common attacks but also assures the fairness property.In 2019,Chistiakovet al.[21]proposed feasibility demonstration of twin-field quantum key ditribution system based on multi-mode weak coherent phasecoded states and show that in principle it can beat well-known fundamental limit of repeaterless quantum communications,i.e.,the secret key capacity of the lossy communication channel.In 2020,Leuchset al.[22]reviewed the R&D advances for quantum communication systems.The last two decades have witnessed tremendous advances in both theoretical developments and successful experimental demonstrations of various quantum communication systems[23–32].
Above quantum communication protocols provide robust security guarantee;however,the reliability of the quantum information transmission in decoherent quantum channel has not been considered,that is,error messages may be delivered to user,or even lost.Hybrid automatic-repeat-request(ARQ) systems [33–35]are used to solve above problems in classical network,but cannot apply to quantum network.Therefore,we present a quantum secure communication system,based on a novel hybrid ARQ scheme using a kind of quantum error correction(QEC)[36–38]code,simultaneously provides robust security guarantee and reliability guarantee.
The organization of this paper is as follows.After introducing our notations and giving an overview of relate work in section II,the proposed scheme is described in section III.Section IV is devoted to discuss the analysis of this scheme.Finally,we present the conclusion in section V.
II.OVERVIEW
In this section,we review the traditional theories relevant to the presented work,that is,quantum logic gates and quantum stabilizer codes.
2.1 Quantum Logic Gates
Quantum logic gates are basic operations on qubits,which are realised by unitary transformations described by unitary matrices.A unitary matrix has the property that its inverse is its complex conjugated,U−1=U†.Single qubit gates are formally described by 2×2 unitary transformations.Some useful single qubit gates and their representations are summarized in the Table1.The first four gatesI,X,Y,Zare equivalent to the Pauli matricesσi,σx,σy,σz,respectively.

Table1.Notations for the common single qubit gates.
It is important to operate on more qubits at the same time as well.A 2-qubit gate that we will make frequent use of is the controlled-NOT gate,which we’ll often refer to as CNOT.CNOT is the prototypical controlled operation with two input qubits,known as the control qubit and target qubit.In terms of the computational basis,the action of the CNOT is given by|c〉|t〉 →|c〉|t ⊕c〉 t,c ∈{0,1};that is,if the control qubit is set to|1〉then the target qubit is flipped,otherwise the target qubit is left alone.Single qubit gates and CNOT gate can be used to implement an arbitrary unitary operation onnqubits,and therefore are universal for quantum computation.
2.2 Quantum Stabilizer Codes
Controlling qubits errors and decoherence is one of the major challenges facing the field of quantum communication.Quantum stabilizer codes,a grouptheoretical structure and subclass of quantum codes,has proved particularly fruitful to meet this challenge.A [n,k]quantum stabilizer code is defined to be the vector spaceVWstabilized by a subgroupWofnqubits Pauli groupGnsuch that−I /∈WandWhasn −kindependent and commuting generators,
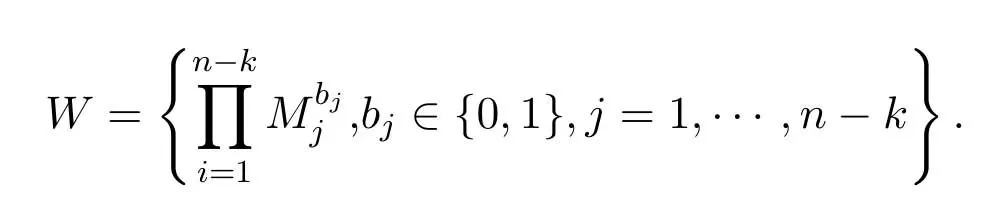
To detect and correct the error states introduced during transmission,then−kgenerators of a[n,k]quantum stabilizer code are used to encode original states,which expand thekqubits tonqubits.The encoding equation is
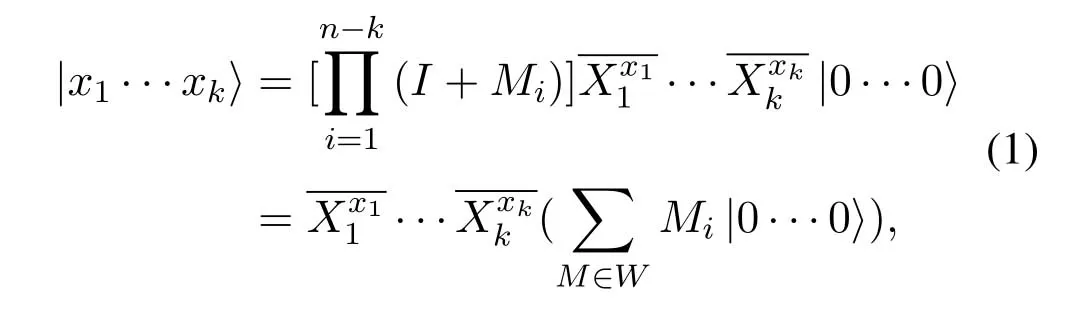
whereMiis thei-th generator of the [n,k]quantum stabilizer code,is X gate performing on a qubitxi,and|0···0〉is spanned byn|0〉.For a logical state,in addition to the need for 1-dimension of space to accommodate the state,a 3n-dimensional Hilbert space is needed to distinguish the three correctable errorsE ∈{ex,ey,ez},whereexis bit flip error that can be corrected by X gate,ezis phase flip error that can be corrected by Z gate andeyis bit and phase flip error that can be corrected by Y gate.Therefore,a(3n+1)-dimensional Hilbert space is needed for a[n,k]quantum stabilizer code,the parametersnandksatisfy

III.PROPOSED SCHEME
The proposed scheme is divided into four processes,that is,preliminary process,transmission process,detection and correction process,and hybrid ARQ process.
3.1 Preliminary Process
We demonstrate an extensible quantum network architecture of transmitting quantum information,which hasM+1 quantum network nodes,as shown in Figure1.This quantum network architecture is many to many,and nodes are connected via quantum channels.LetS={S0,S1···,SM}be a set of nodes.At any point of time,any subset ofSmay decide to execute the protocol.A node may execute many protocol instances in parallel.SupposeStis the transmitter,Sris the receiver,t,r ∈{0,1,···,M}.Step 1:Stsends information qubits toSr,the qubits will be encoded by a[n,k]quantum stabilizer code at first.The information qubits blockλ={|ϕ1〉,|ϕ2〉,···,|ϕm∗k〉}hasm ∗kqubits,m ∈{1,2,···}.|ϕj〉=α|0〉+β|1〉(α2+β2=1)is thej-th qubit ofλ.Eachkqubits inλare spanned into a quantum logical state|ψi〉.|ϕx〉⊗|ϕy〉is a product state of|ϕx〉and|ϕy〉.After spanning,Stobtains a logical states blockλ′with m product quantum states,λ′={|ψ1〉,|ψ2〉,···,|ψm〉},where
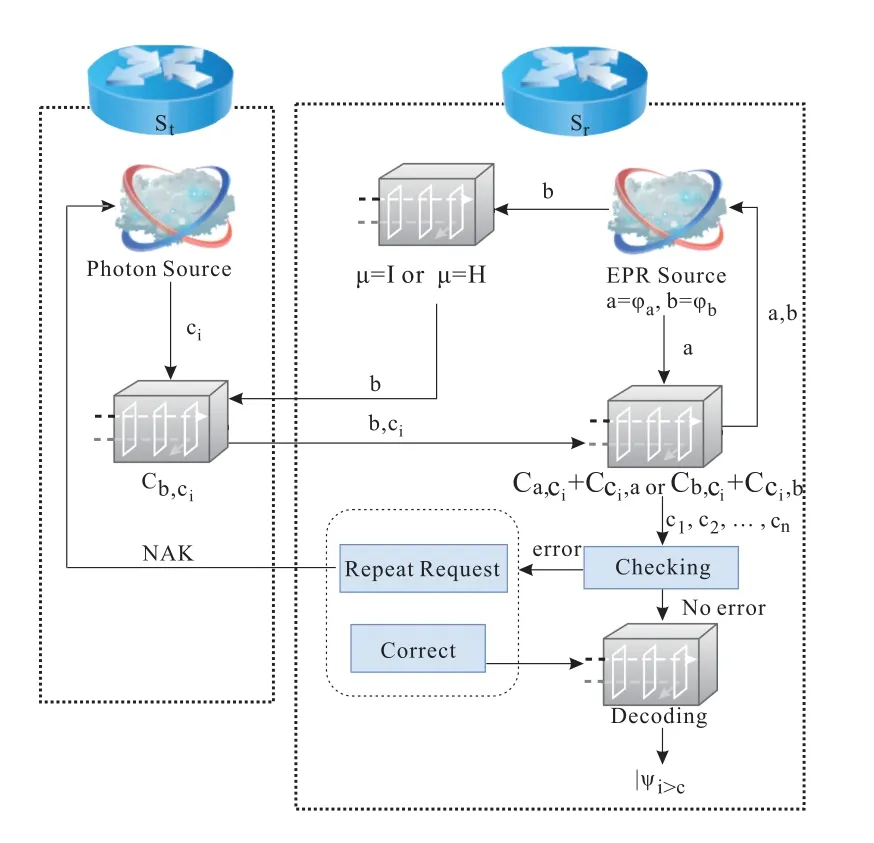
Figure1.Extensible quantum network architecture.
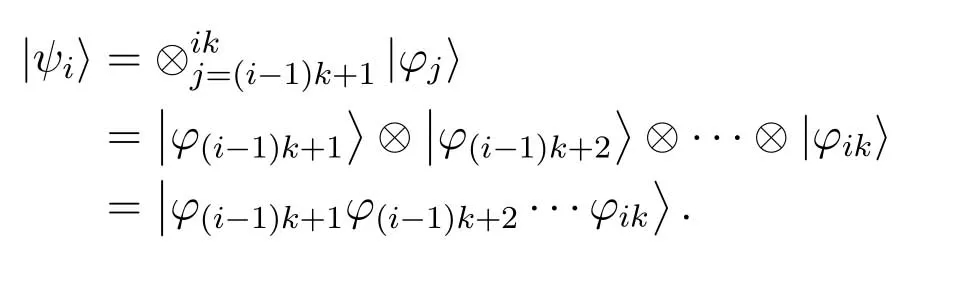
Step 2:Encode every quantum logical state inλto the codeword state by Eq.(1),which is accomplished by using quantum gates.Thek-qubit state|ψi〉is expanded ton-qubit state|ψi〉c.After encoding,Stobtains a transmission blockγwith m codewords,
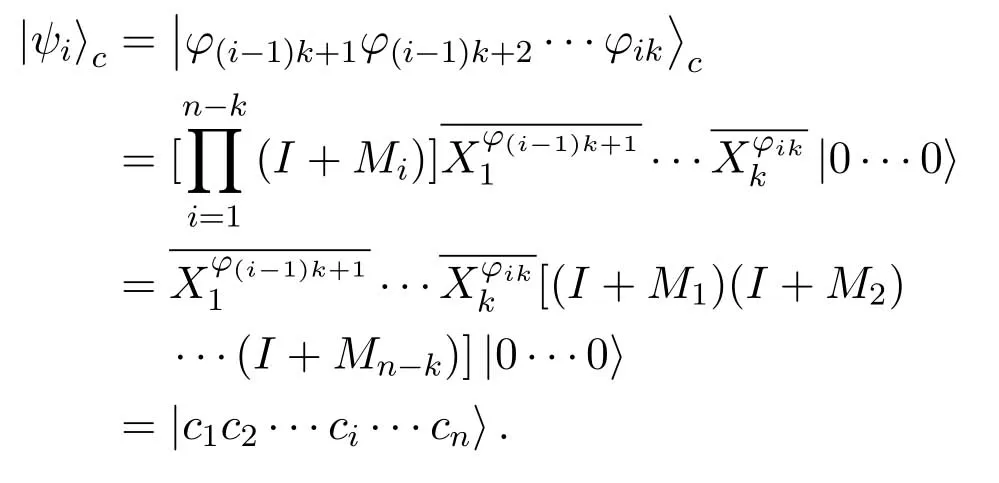
3.2 Transmission Process
Step 3:StsendsγtoSrin units of|ψi〉c.The transmission process is based on a quantum entangled state.Therefore,a two-photon entangled state ofϕaandϕbis prepared firstly.The two-photon entangled state
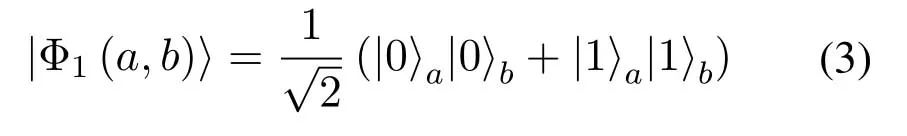
is the maximum entangled state ofHm=Ha ⊗Hbin Hilbert space,whereaandbrepresentϕaandϕb,respectively.Perform Hadamard gate on|Φ1(a,b)〉,we get
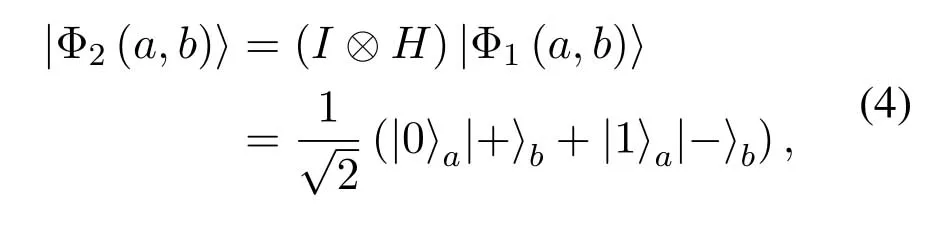
where|±〉=|0〉±|1〉.For a message photonciin|ψi〉c=|c1c2···cn〉,there are
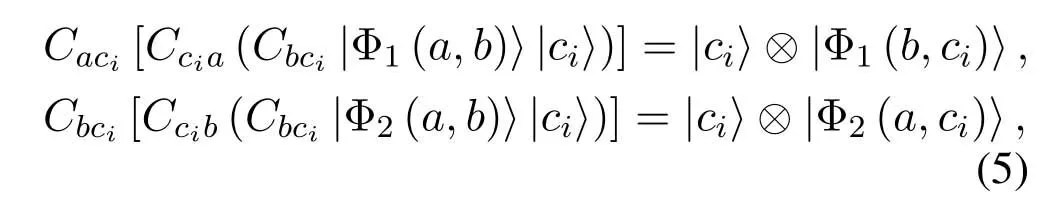
where|ci〉is the state ofci,Caci,Ccia,Cbci,Ccibare CNOT operations.For example,Cacimeans a CNOT gate performs on photonsϕaandci,whereϕais control qubit andciis target qubit.Based on Eq.(5),the transmission process of|ψi〉cis as follows.
Step 4:Srperforms a random single qubit gateµ ∈{I,H}on the photonϕb,and keepsϕawhile sendingϕbtoStvia quantum channel.Thus,StandSrwill randomly share the quantum states|Φ1(a,b)〉or|Φ2(a,b)〉.Stprepares photonciaccording to|ψi〉c,and performsCbcion photonϕbandci,and then sendsϕbandcitoSr.Srreceivesϕbandci,and then gets message state|ci〉by measuring according toµselected in advance.Whenµ=I,SrperformsCaci,Cciaonϕaandcirespectively,and gets|ci〉by measuringϕa.Whenµ=H,SrperformCbci,Ccibonϕbandcirespectively,and gets|ci〉by measuringϕb.Repeatingntimes,andSrreceives|ψi〉c.The codeword transmission process is shown in Figure2.
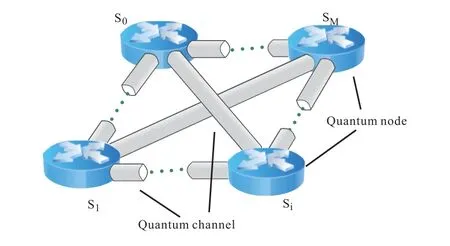
Figure2.Codeword transmission process.
3.3 Detection and Correction
Step 5:Srgenerates a check matrix,denoted asHS,to detect the received|ψi〉c.HSis constructed by the [n,k]quantum stabilizer codes generators.SupposeEis an error that corrupts|ψi〉cafter transmission.IfEis an correctable error,E ∈{ex,ey,ez}commutes or anti-commutes with the generatorsMi ∈{M1,M2,···,Mn−k},giving
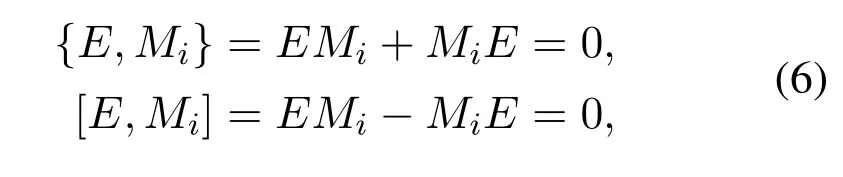
then we haveMiE(ϕi)=−EMi(ϕi)=−E(ϕi)orMiE(ϕi)=EMi(ϕi)=E(ϕi).It shows that if aMianti-commutes withE,the eigenvalue of the error state becomes−1.HSis constructed as

hasn −krows and 2ncolumns.HZcommutes withMiand anti-commutes withex.HXcommutes withMiand anti-commutes withez.HX+HZcommutes withMiand anti-commutes withey.
Step 6:SrusesHSto measure|ψi〉c,and obtains a error syndrome matrix,denoted asλe.According toλe,the type ofEis detected.The corresponding Pauli gate is then used to correct the error.
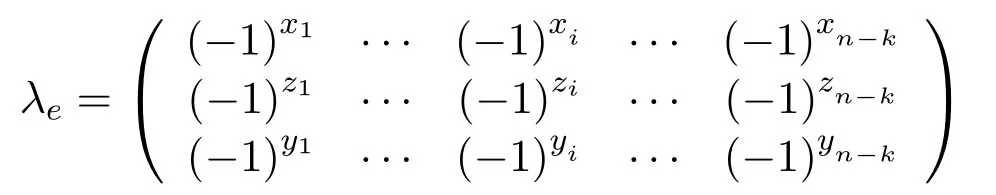
has 3 rows andn −kcolumns,andxi,zi,yi ∈{0,1}.The three rows of the matrix correspond toex,ez,ey,respectively.If all elements inλeare 1,it indicates no error occurs in the transmission process.If the element of thex-th row andy-th column in the matrix becomes−1,it indicates that they-th qubit in|ψi〉chas an error corresponding to thex-th row.The quantum gate,which anti-commutes withE,is executed to correct|ψi〉c.In particular,ifEis a uncorrectable error,a retransmission will be initiated.
3.4 Hybrid ARQ Process
Step 7:When|ψi〉cis detected uncorrectable,Srrejects|ψi〉c,and sends a negative-acknowledgment(NAK)toSt.Otherwise,Sraccepts|ψi〉c,and sends a positive-acknowledgment(ACK)toSt.
A transmitter buffer (TB) is provided atStto store the copy states of transmitted codewords.IfStreceives NAK of|ψi〉cor no acknowledgment of|ψi〉cin a round-trip delay time,a retransmission is initiated,and the copy state of|ψi〉cis sent toSr.Retransmission will continue until|ψi〉cis successfully accepted.
A receiver buffer (RB) is provided atSrto store the error-free received codewords following a uncorrectable codeword,ensures the codewords are deliverd to user in order.When the first negatively acknowledged coedword in RB is successfully accepted,the error-free codewords in consecutive order will be released until the next uncorrectable codeword is encountered.
SupposeNis the number of codewords that can be transmitted during a round-trip delay period.Consider the size of the RB isN,that is,RB can store N codewords simultaneously.Every codeword inγhas sequence number(SN).The range of SN is 1,2,···3N.These numbers are used cyclically,that is,a new codeword following the codeword with SN of 3N has numbered with one again.Next,we describe this process from the perspective of transmitter and receiver,respectively.
3.4.1 Transmitter Operation
Step 8:Firstly,the codewords inγare stored and numbered in the input queue bySt.Secondly,Stsends codewords in order,and stores the copy of the current sending codeword in TB.When the current sending codeword is|ψi〉c,the forward index (FWX) of|ψi〉cis computed.In this operation,FWX is denoted asfT.Mathmatically,
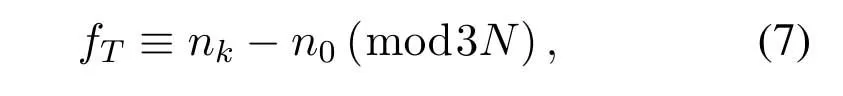
wherenkis the SN of|ψi〉c,andn0is the SN of the earliest NAK or unACK codeword in TB.fTis the remainder resulting from dividingnk −n0by 3N,obviously,0≤fT <3N.According tofTand acknowledgment,Stdecides to transmit the next codeword in the input queue or initiate a retransmission.The rules of transmitter operation are shown as follows:
Case 1.If fT Case 2.If fT Case 3.If fT=0,all the codewords in TB with FWX≥N are moved back to the input queue.These codewords have been transmitted;however,the RB has no space to store them(buffer overflow).Therefore,these codewords will be retransmitted. Case 4.If fT ≥N,the first codeword in the input queue is the next one to be transmitted.(In this case,|ψi〉c maybe a codeword that was moved back to the input queue from TB owing to the RB overflow.) 3.4.2 Receiver Operation Step 9:The receiver operation is devided into two parts,that is,normal-state operation and block-state operation.If|ψi〉chas no error or correctable errors,Srsends an ACK toSt,|ψi〉cis delivered to the user in correct order,and RB is empty.In this event,the receiver is said to be in the normal state.If|ψi〉chas uncorrectable errors or|ψi〉cis out of order,Srsends a NAK toSt,and enters the block state.In block state,no codeword is delivered to user. wherenkis the SN of|ψi〉c,nmis the SN of the last accepted and delivered codeword,neis the SN of the earliest codeword in RB,andnlis the SN of the last codeword (or the codeword has a reserved space) in RB.Obviously,0≤fR <3N,0≤lf <3N,and 0≤lb <3N. According tofRandλe,the rules of normal-state operation are as follows: Case 5.If fR=1and λe is a error-free pattern,SN of|ψi〉c is in correct order and|ψi〉c has no error.|ψi〉c is to be accepted and delivered to users directly,and an ACK of|ψi〉c is to be sent to St.Sr detects the next codeword and stays in normal state. Case 6.If fR=1and λe is a correctable error pattern,SN of |ψi〉c is in correct order and the error in|ψi〉c can be corrected.|ψi〉c is to be delivered to users after corrected,and an ACK of|ψi〉c is sent to St.Sr detects the next codeword and stays in normal state. Case 7.If fR=1and λe is an uncorrectable error pattern,|ψi〉c is to be discarded and the first location of RB is reserved for |ψi〉c.A NAK is sent to St,and Sr enters the block state. Case 8.If1 Case 9.If1 Truly the man would have had no objection to be rich, but he thought to himself: I must first ask my daughter about this, 14 so he went in and told them that there was a great white bear outside who had faithfully promised to make them all rich if he might but have the youngest daughter. Case 10.If1 Case 11.If fR >N or fR=0,|ψi〉c is a codeword that has been preciously accepted and delivered,the acknowledgment has been lost and caused the retransmission.|ψi〉c is to be ignored and an ACK is to be sent to St.Sr stays in the normal state and processes the next incoming codeword. Supposeniis the SN of the last codeword delivered to the user.According tolf,lb,λeandni,the rules of block-state operation are as follows: Case 12.If lf Case 13.If lf Case 14.If lf Case 15.If lf ≥N and lb ≤2N,|ψi〉c is a codeword that has been preciously accepted and delivered,an ACK of|ψi〉c is to be sent to St.Sr stays in the block state and processes the next incoming codeword. Case 16.If lf ≥N and lb >2N,|ψi〉c is a new codeword,due to the limitted size of RB,it will be rejected.Sr sends a NAK of|ψi〉c and stays in the block state. The Security of this protocol depends on every process of communication between a transmitter and a receiver.The secret data is encoded by quantum stabilizer codes and transmitted through quantum channel.There is no information revealed.However,attacks by eavesdroppers(Eve)could still exist.Security analyses under typical attacks are given as follows. 4.1.1 Attack via Bell method The operatorµ ∈ {I,H}in transmission prosess is randomly selected bySr,two different quantum keys,denoted|Φ1(a,b)〉and|Φ2(a,b)〉,are randomly generated.They satisfy〈Φ1(a,b)|Φ2(a,b)〉 /=0,which means they are nonorthogonal.Therefore,it is impossible to distinguish two quantum states using Bell method.In addition,since the entangled states|Φ1(a,b)〉and|Φ2(a,b)〉will not be affected by the operation of Eq.(5),that is,the security of this two quantum keys will not be affected by the encryption and decryption algorithm in the communication process,thus the keys|Φ1(a,b)〉and|Φ2(a,b)〉can be used multiple times. 4.1.2 Attack via ancilla particle Suppose Eve intercepts the particle sent by transmitter,which will be entangled with an ancilla|e〉prepared by Eve.The unitary transformation denotedUthat implement on transmitter’s particle does not change the state of single photons. whereUcan be written as where|a|2=|a′|2,|b|2=|b′|2,and|a|2+|b|2=1.So the probability of Eve being detected is the eavesdropping brings a certain amount of error rate,and it must be detected. According to the information theory,the amount of maximum accessible information in quantum system is limited byHolevolimit: whereS(ψ) is the Von-Neumann entropy of stateis a state prepared in probabilitypi.If communicating parties prepare states|0〉and|1〉,then the information entropyH(p)=Thus the Von-Neumann entropy of Eve isS(ψ′)=0 Throughput efficiency is defined as the ratio between the average number of quantum codewords successfully received by the receiver per unit time and the total number of quantum codewords sent by the transmitter per unit time.Suppose a hybrid ARQ system uses a[n,k]quantum stabilizer code for error detection and correction.First,definePcis probability that the receiving codeword contains no error,and contains detectable and correctable errors.Pdis probability that the receiving codeword contains detectable but uncorrectable errors.Peis probability that the receiving codeword contains undetectable errors. Obviously,Pc+Pd+Pe=1.These three possibilities are determined by channel noise.An uncorrectable codeword will be rejected and retransmitted.Therefore,the probability that a receiving codeword is accepted by the receiver isP=Pc+Pe.The mathematical definition of error rateP(E)is which is determined by the quantum stabilizer code parametersnandk.For the usual situation wherePe ≪Pc,P ≈Pc.The probability that a codeword being retransmitted is For the receiver successfully accept a codeword,the average number of retransmissions required is The throughput efficiency of the hybrid ARQ scheme with the[n,k]quantum stabilizer is It can be seen that the throughput efficiency of this hybrid ARQ scheme depends on the channel noise and the parametersn,kof the quantum stabilizer code.According to Eq.(2)and Eq.(17),the relationship betweenn,k,andηharqis shown in Table2. Table2.The relationship between n,k,and throughput efficiency of this protocol. In [39],the transmitter sends secret qubits in the noisy quantum channel.Half of the qubits with different measurement bases are discarded,and half of the remaining qubits are consumed for error correction of Calderbank-Shor-Steane(CSS)codes.[39]has a throughput efficiency of 0.2500P.In[40],the transmitter sends 2n+δqubits,wherenqubits are used to detect errors.The throughput efficiency of [40]is 0.5000P.According to Table2,whenn=10,ηharqreaches 0.5000P.Whenn=1012,ηharqis as high as 0.9881P.Therefore,our protocol performs well in terms of throughput efficiency. It is proposed the novel hybrid ARQ protocol for the quantum communication system using quantum stabilizer codes and demonstrated its security with respect to against attacks.The reliability of this protocol is guaranteed by the automatic retransmission scheme of ARQ,and the error-correcting scheme of quantum stabilizer codes.The security of this protocol is guaranteed by the special properties of quantum entangled states.Therefore,the protocol is realized in current condition. ACKNOWLEDGEMENT The work is supported by was supported by the Shandong Province Higher Educational Science and Technology Program (Grant No.J18KZ012),and the National Natural Science Foundation of China (Grant No.11975132,61772295),and the Shandong Provincial Natural Science Foundation,China (Grant No.ZR2019YQ01).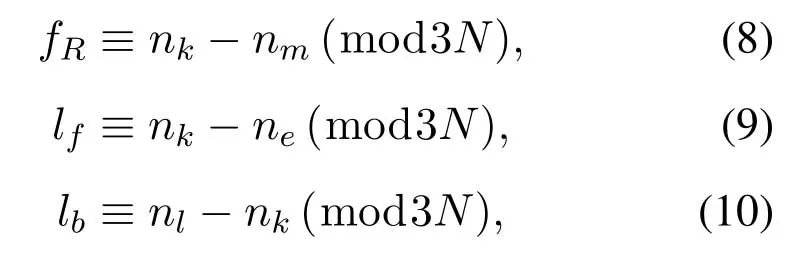
IV.ANALYSIS
4.1 Security Analysis Under Typical Attack
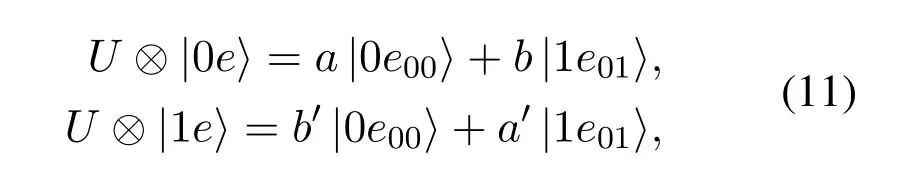
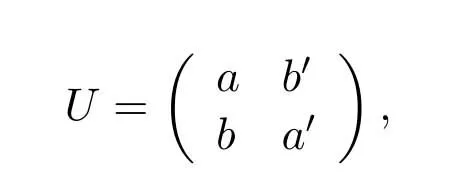
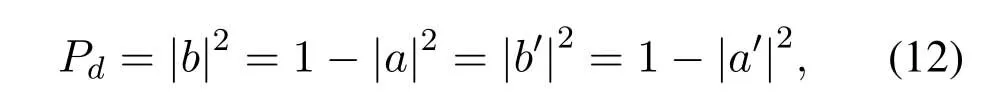
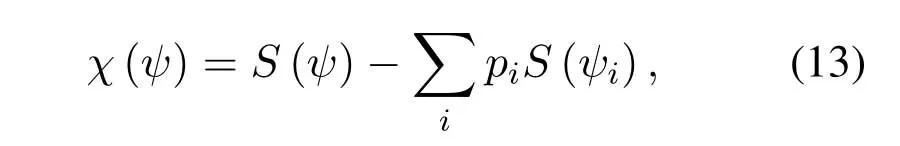
4.2 Throughput Efficiency Analysis
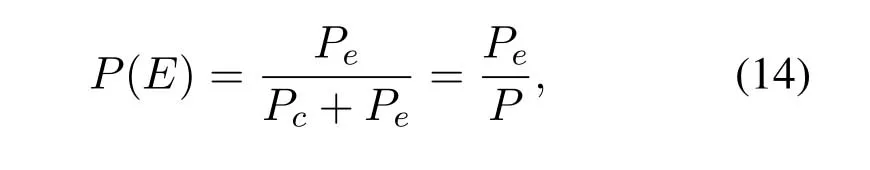
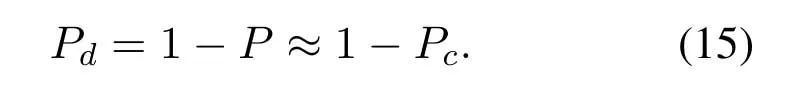
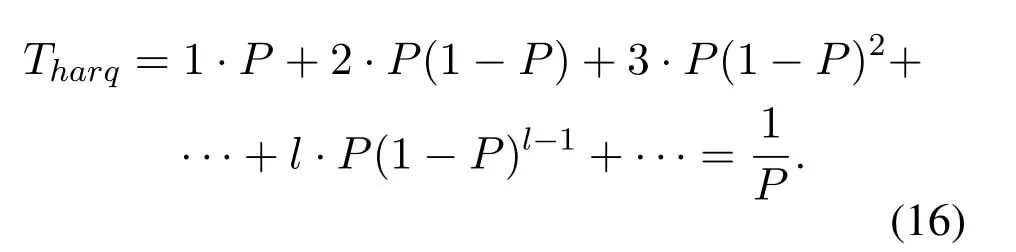


V.CONCLUSION

