Coded Modulation Faster-than-Nyquist Transmission with Precoder and Channel Shortening Optimization
Hui Che,Yong Bai
1 School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China
2 School of Information and Communication Engineering,Hainan University,Haikou 570228,China
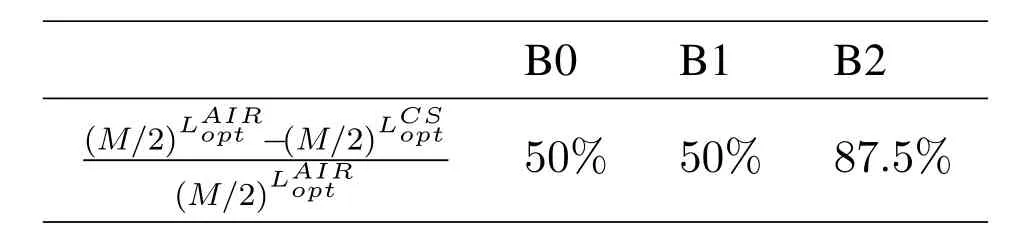
Abstract:Faster-than-Nyquist (FTN) signaling can improve the spectrum efficiency(SE)of the transmission system.In this paper,we propose a coded modulation FTN(CM-FTN)transmission scheme with precoder and channel shortening(CS)optimization to improve bit error rate (BER) performance and reduce the complexity of FTN equalizer.In our proposal,the information rate(IR)or spectral efficiency(SE)is employed and verified as a better performance metric for CM-FTN than the minimum Euclidian distance(MED).The precoder of CM-FTN is optimized for maximizing the IR criterion using the bare-bones particle swarm optimization (BB-PSO) algorithm.Further,a three-carrier CM-FTN system model is used to capture the broadening effect of precoder.Also targeting for the IR maximization,the inter-symbol interference (ISI) length for CS is optimized to reduce the receiver complexity without performance loss.Simulation results demonstrate that our method has a 0.6dB precoding gain compared with the nonprecoding scheme and a maximum of 87.5% of the complexity of FTN equalizer is reduced without BER loss.
Keywords:faster-than-Nyquist;coded modulation;information rate;minimum Euclidian distance;precoder;channel shortening
I.INTRODUCTION
Spectrum efficiency (SE) is a key performance indicator for transmission systems.In the future communication system,high SE is required because of the explosive growth of data traffic.Faster-than-Nyquist(FTN)signaling can improve the SE by packing the transmission interval of the neighboring shaping pulses and introduces inter-symbol interference(ISI)due to the violation of the Nyquist zero-ISI theorem.Mazo [1]first introduced the FTN using sinc pulse in 1975,and Liveris[2]put forward a more practical FTN scheme with raised-cosine pulses in 2003.Rusek introduced the multi-carrier FTN in [3][4]and the FTN into multiple-input multiple-output(MIMO)system in [5].The traditional FTN mainly considers the impact of the minimum Euclidean distance(MED)on system performance.The FTN can work together with coded modulation as CM-FTN in a more practical system and the system performance in such a transmission system needs to be investigated.
In this paper,we investigate a CM-FTN transmission scheme with precoder and channel shortening(CS)optimization to improve bit error rate(BER)performance and reduce the complexity of FTN equalizer.Firstly,we should find a robust and reliable metric as a measure of CM-FTN performance for precoder optimization.This metric must be consistent with the BER performance of the CM-FTN.There are two metrics in the FTN related literature,namely the MED and information rate(IR).
1.1 MED Vs.IR
Mazo employed MED to measure the performance of the FTN system [1].The FTN signal [1]can be expressed as

wherexnis theuncodedbinary transmit symbol,φ(t)is the ideal sinc pulse,the FTN symbol periodTs=τT,τis the time packing factor (TPF) andTis the Nyquist symbol period forτ=1.For the FTN system,Mazo in [1]showed that the lower bound for maximum likelihood sequence estimation (MLSE) is Forney’s lower bound[6],i.e.,
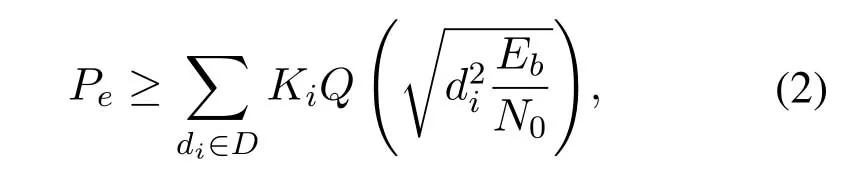
whereDdenotes the set of all possible normalized Euclidian distancedi,Kidenotes a weighting factor which is determined by the pattern of error sequences ofd2i,andQ(·) is the cumulative Gaussian function[6].Because of the exponential decrease of the Gaussian function,(2) will be dominated by the term involving the normalized minimum Euclidian distance(MED)dminofDat the high signal-to-noise ratio(SNR),
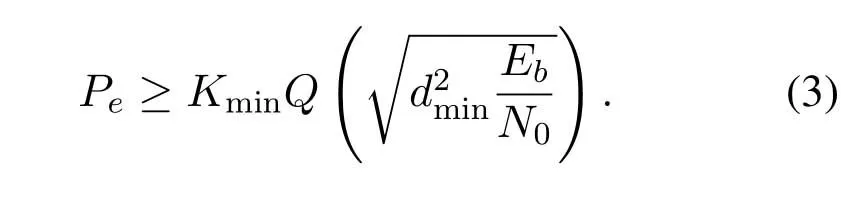
This inequality is tight for high SNR orEb/N0.d2mindrives the asymptoticrawerror probability and is a measure of a systems noise immunity.The wordrawis to emphasize that the system does not consider forward error correction (FEC) and therawBER is the BER for output of the FTN equalizer.FTN signaling does not affect the MED of uncoded binary sinc pulse transmission,and hence the asymptoticrawerror probability in theory,as long as the TPFτis above the Mazo limit[3][7][8][9].Therefore,many past papers analyzed and optimized the FTN system based on the MED criterion or Mazo limit.
For the first time,Rusek and Anderson have analyzed FTN signaling from the perspective of information theory and obtained the constrained capacities of FTN with Gaussian source in [10].FTN signaling significantly benefits from excess bandwidth[10].For the finite alphabet,the IR of the ISI channel and its bounds based on auxiliary channel(or mismatched channel)have studied in[11][12][13].Our study finds that the IR or SE is a robust and reliable metric as a measure of CM-FTN performance;on the other hand,the MED is not a robust and reliable metric as a measure of CM-FTN performance.TherawBER of the CM-FTN at an operating point generally corresponds to the low SNR region.However,(2) will be determined at low to medium SNR by all possible normalized Euclidean distance and not just the MED.The MEDd2mincannot yield reliable information of FTN at the low SNR.The MED and IR cannot always be harmonious in the ISI system.This situation also exists in the Nyquist system[14].The maximal MED cannot ensure a large the average mutual information of coded modulation(CM-AMI)or average mutual information of bit-interleaved coded modulation (BICM-AMI) in the Nyquist system.Maximizing MED between the constellation points,unfortunately,could not ensure a large IR and IR considers the Euclidean distance set beside the MED in[14].
1.2 Convolutional Precoding
At present,there are three main precoding methods for FTN:FIR filtering(convolution),IIR filtering,and matrix decomposition [15–17].IIR filtering includes two methods,Tomlinson-Harashima precoding(THP)[18–21]and Linear pre-equalization (LPE) [22,23].The IIR filtering and matrix decomposition are primarily concerned with reducing the complexity of the receiver.The convolutional precoding(FIR filtering)is primarily concerned with improving the performance.This paper focuses on the convolutional precoder.
The PSD of the transmission waveform can be changed by convolutional precoding.This reform in the transmission waveform may result in an improvement in MED and IR.Said[24]and Rusek[25]optimized the convolutional precoder by maximizing the MED.Since the MED is not a robust and reliable metric as a measure of CM-FTN performance,we propose to optimize the convolutional precoder by maximizing the SE of CM-FTN and some results can be found in[26].The relationship between IR and SE is given in(16).Moreover,precoding an FTN signal may significantly alter and broaden its transmission spectrum[27].We employ a 3-carrier FTN system model to capture the broadening effect for convenience.In[28],a proper transmission filter has been designed with the Gaussian source and CS detector to improve the mutual information.However,it may not be proper for the FTN transmitter withM-ary finite alphabet.The SE of CM-FTN based on CS is evaluated as the fitness function for precoder optimization in this paper.
In order to maximize the SE of FTN with a finite alphabet,a particle swarm optimization (PSO)can search a precoder good enough for the CM-FTN system employing a CS detector.The SE is a nonlinear function of the precoder b,and the traditional linear optimization algorithm may not suitable here.Two evolutionary computation paradigms can be used for nonlinear function optimization,i.e.,genetic algorithm (GA) and particle swarm optimization (PSO).The PSO has better ergodicity than GA [29].Compared to GA,PSO is easier for implementation and there are few parameters to be adjusted for PSO[30].PSO has the same effectiveness(finding the true global optimal solution) as GA but with significantly better computational efficiency [31].The PSO method based on bird flocking is one of the most famous artificial intelligence (AI)-based optimization algorithms[32].It is an intelligent approach for the optimization of nonlinear functions.A swarm of particles is initiated and fly in the solution space to find the optimal solution.Each particle has a velocity and position vector.The bare-bones PSO(BB-PSO)algorithm is conceptually the simplest of all PSOs.The velocity and position update rules in PSO are substituted by sampling from a probability distribution[33][34].Each particle in BB-PSO only has a position vector and eliminates the velocity vector.Both original PSO and BB-PSO may suffer from premature convergence when solving complex multimodal problems.[35]theorized that populations with fewer connections might perform better on highly multimodal problems,while highly interconnected populations would be better for unimodal problems.Based on this idea,the neighborhood search strategies are applied to the BB-PSO to find the best precoder for CM-FTN.Peng et al.in[36]considered SE maximization for multi-carrier FTN.However,they approximated the ISI and ICI as Gaussian noise and employed the approximative memoryless channel.With the increase of the SNR,the influence of ISI and ICI gradually exceeds the effect of noise for their method.In theory,the information rate no longer increases with the increase of the SNR after the SNR exceeds a certain threshold.The larger the ISI and ICI,the lower the threshold.
1.3 Receiver with Channel Shortening
The FTN can be seen as the symbolic convolutional coding over the field of the real or complex domain.The complexity of the maximum posterior probability(MAP)receiver for FTN isO(ML),whereMis the constellation cardinality andLis the ISI length.The ISI length is very large for FTN and the original BCJR algorithm detection becomes unmanageable because of high-complexity.In order to reduce the computational complexity,there are six methods as follows.Firstly,the simplest solution is that the BCJR detector works with a truncated version of the channel response [2]and it may yield poor performance unless the truncated part of the channel response has negligible power.Secondly,LPE[22]makes the FTN equivalent to an orthogonal transmission.However,the method LPE is failed whenτ <1/(1+β),whereβis the roll-off factor of root raised-cosine(rRC).Thirdly,a frequency-domain equalization (FDE) based on a minimum mean square error(MMSE)criterion is employed for FTN [37].However,it is a suboptimal algorithm,and the cyclic prefix length is too long for FTN with lowτ,which reduces the SE of FTN.Fourthly,the sum-product algorithm (SPA) with the factor graph (FG) [38]for FTN makes the complexity growing linearly with the number of interferers,and it is not suitable for FTN with lowτdue to too long ISI length.Fifthly,the MBCJR based on Forney[39][40]or Ungerbocek model [41]selects a portion states of allMLstates and is a breadth-first algorithm.However,the MBCJR detector may lead to low quality of soft output and updates the state space at each time index.Sixthly,the channel shortening(CS)uses an information-theoretic framework to reduce the ISI lengthLfor the BCJR detector,and the BCJR detector can offer satisfactory performance with reasonable complexity for CM-FTN.
CS is a technique originally proposed by Falconer and Magee in 1973[42]and improved in[43]for general linear channels,such as MIMO and ISI channels.Li et al.[44]have proposed the code based channel shortening (CCS) algorithm to reduce the complexity.The cascade of FTN and output-retainable convolutional code(ORCC)in[44]has improved the energy efficiency at the expense of reduced SE.By using an information-theoretic framework,the optimal front-end filter for CS can be formulated in closed form.For the CS in [43],there are two parameters that are determined firstly,namely the power spectrum of the transmitted signal and the given ISI length considered at the detector.The power spectrum of the transmitted signal is optimized by convolutional precoder with IR or SE criterion.The complexity of FTN equalizer is much higher than that of IR calculation.The FTN equalizer needs to consider both forward and backward recursions,while IR calculation only considers forward recursion.The FTN equalizer needs to save the log-likelihood ratio(LLR)values for all states in forward and backward recursions.It is not necessary to save the LLR values for all states in forward recursion,because IR calculation only considers the accumulated results.Due to the iteration between the FTN equalizer and the LDPC decoder,the complexity of the FTN equalization further increases.Therefore,with limited computing and storage resources,IR calculation can use a larger ISI length to achieve the true IR and the FTN equalizer should use a smaller ISI length.A smaller ISI length may cause equalization losses.There is a trade-off between complexity and performance.The lower bound on the true IR is achievable by a maximum-likelihood decoder with the same ISI length [11][13][43].The calculation of the lower bound needs a smaller ISI length than IR calculation.The ISI length for the CM-FTN is optimized according to the criteria of the lower bound on IR close to the true IR,which minimizes ISI length without performance loss.CS optimization relies on precoder optimization.However,the ISI length of CCS in[44]is optimized by the MED metric.Li et al.in [45]proposed the pre-equalized interference cancellation for FTN to reduce the complexity.They also approximated the ISI as well as ICI as Gaussian noise and updated the equalizer tap vector with the linear minimum mean square error (LMMSE) criterion.Their method has the same problems as[36]and LMMSE is not the optimal criterion in theory.
In summary,we have the following main contributions in this paper.
• We find that IR or SE is a better performance metric for the CM-FTN rather than the MED.
• We optimize the precoder of CM-FTN for maximizing SE by introducing BB-PSO algorithm.
• We minimize the ISI length for the channel shortening in the CM-FTN to achieve the lower bound close to the true IR without performance loss.
The paper is organized as follows.Section II presents the 3-carrier system model for CM-FTN transmission with precoder and CS.Section III investigates precoder and CS optimization based on the IR criterion.Section IV provides theoretical results and Monte-Carlo simulation results.Section V offers concluding remarks.
II.SYSTEM MODEL
The system model for CM-FTN transmission with 3-carriers modulation is illustrated in Figure1.In the transmitter,Kinformation bits u=[u1,···,uK]Tare encoded by a (N,K) binary channel encoder to yield a lengthNcodeword c=[c1,···,cN]T,whereci ∈{0,1}.The code rate of the channel encoder isr=K/N.The codeword c is permuted by a random bit-interleaver with interleave lengthN.The bitinterleaver’s output d feeds theM-ary signal mapper which employs a quadrature amplitude modulation(QAM)and Gray labelling.x=[x1,···,xNm]Tis a symbol sequence,wherexiis aM-ary symbol,m=log2MandNm=N/m.M-ary symbol sequence x is delivered to the precoder b and then feeds the FTN modulator.The FTN modulator employs theT-orthogonal rRC pulse with a roll-off factorβas the shaping pulseh(t).In order to maintain almost the same PSD,the shaping pulse has a time-truncation to±ζTaroundt=0 andζ=30 in this paper.The time-truncation toh(t) leads the spectrum spreading.A carrier FTN signal can be expressed,
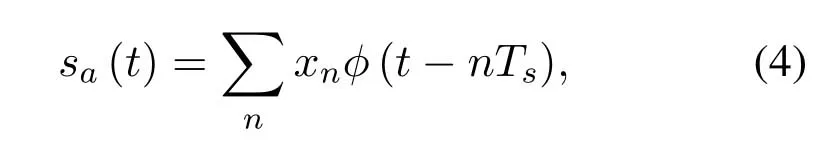
whereTsdenotes the FTN symbol period andφ(t)is the reform of transmission wave form,
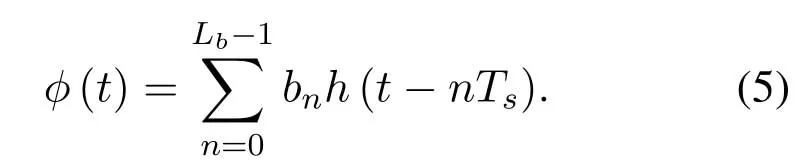
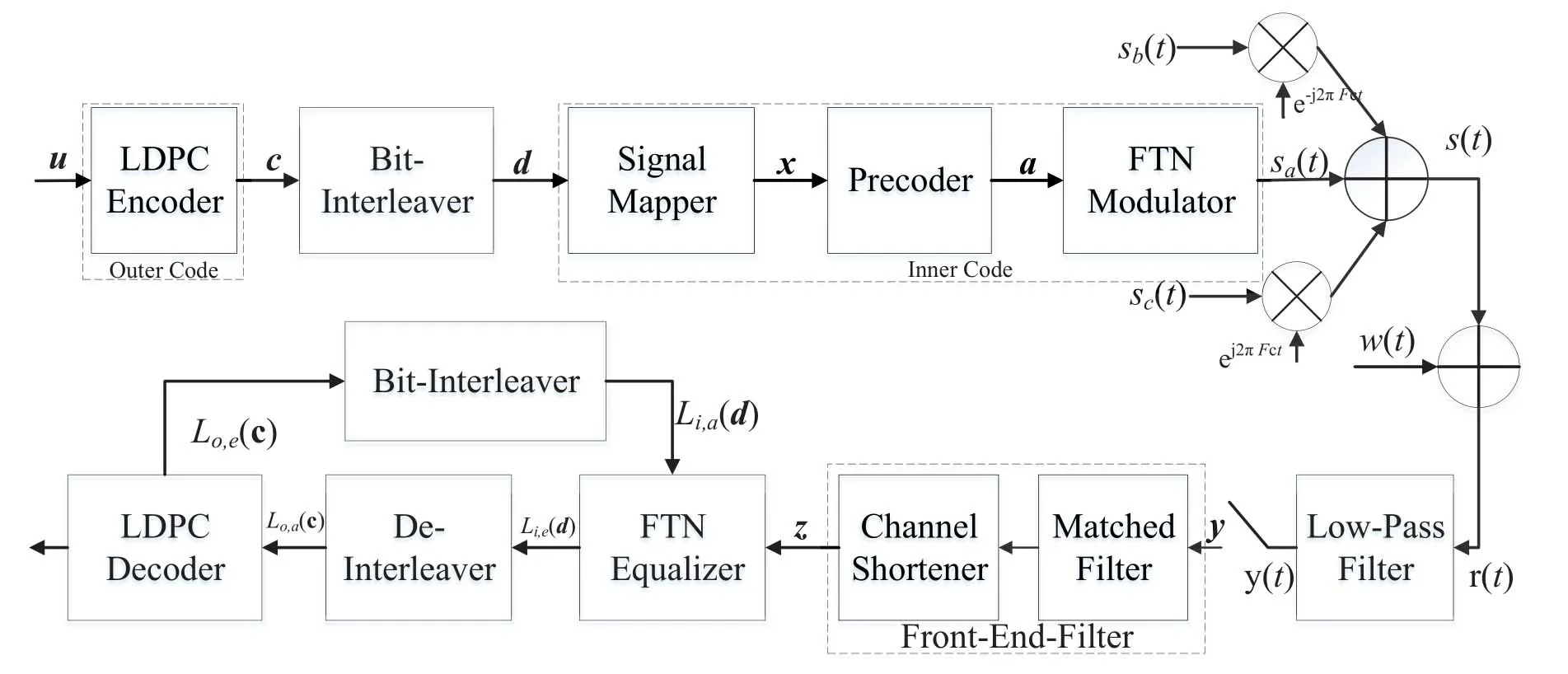
Figure1.Coded modulation FTN transmission system with precoder and channel shortening.
Lbis the support of b,i.e.,the precoder b=[b0,···,bLb−1].The FTN symbol periodTs=τT,whereτis the time packing ratio (TPR) andTis the orthogonal symbol period.Theφ(t) has unit energy,i.e.∞−∞|φ(t)|2dt=1.The upsampler between the precoder and FTN modulator is optional whenτ ≤1/(1+β).This upsampler is essential whenτ >1/(1+β)[22].This paper pays attention toτ <1/(1+β)and does not use the upsampler.It is obvious that (4)constitutes symbolic convolutional coding over the real field.Meanwhile,(4) is a filtering process,and it can be treated as ISI.Precoding an FTN signal may significantly alter and broaden its transmission spectrum[27].We employ a three-carrier FTN system model to capture the broadening effect,
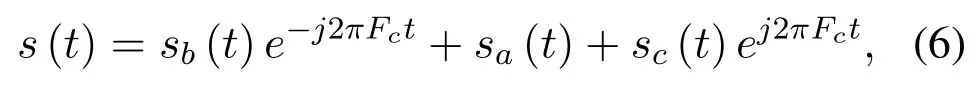
where the synchronous carriessb(t) andsc(t) employ the same signal processing assa(t),and the subcarrier spacingFc=µW,whereµis the frequency packing ratio (FPR);Wis the orthogonal subcarrier spacing andW=(1+β)/T.When 0.5<µ ≤1,the central carrier signalsa(t) is mainly affected by adjacent-channel interference(ACI),sb(t)e−j2πFctandsc(t)ej2πFct.The precoder b has an important impact on ACI.
The three-carrier FTN signals(t) is transmitted over the AWGN channel and the received signal is given byr(t)=s(t)+w(t),where the white Gaussian noisew(t)has two sides PSDN0/2.
We evaluate the ultimate performance limits of this communication system where single-carrier detection[46]is employed at the receiver side.The low-pass filter(LPF)picks up the valid signal from received signalr(t)for the FTN signalsa(t).An ideal low pass filter(ILPF)is employed in this paper and its bandwidth isW.In order to prove the superiority of the IR in theory,we use an ILPF which will not cause IR loss.In practical applications,the ILPF can be replaced by an rRC filter with a small roll-off factor.The output of ILPF is sampled everyTssecond.The sampled signal y pass through the front-end-filter hr,which consists of a matched filter and channel shortener.The receiver employs a reduced-complexity max-log-MAP symbol FTN equalizer based on the Ungerboeck observation model[47]together with the CS method[43][28].The CS algorithm calculates a front-end-filter hrand a target response gr.The BCJR algorithm based on the Ungerboeck observation model[48]accepts the target response gras the ISI channel and works on the mismatched channel model.The mismatched conditional probability distribution function(PDF)
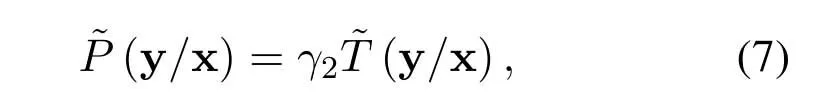
whereγ2[49]is independent of x,
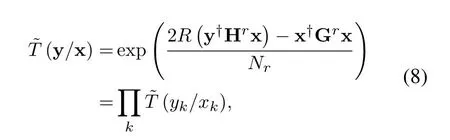
(·)†denotes Hermitian transpose andNris the mismatched noise density[43].The mismatched channel
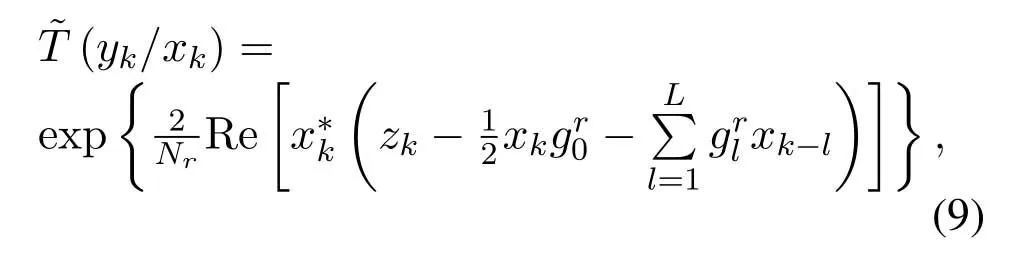
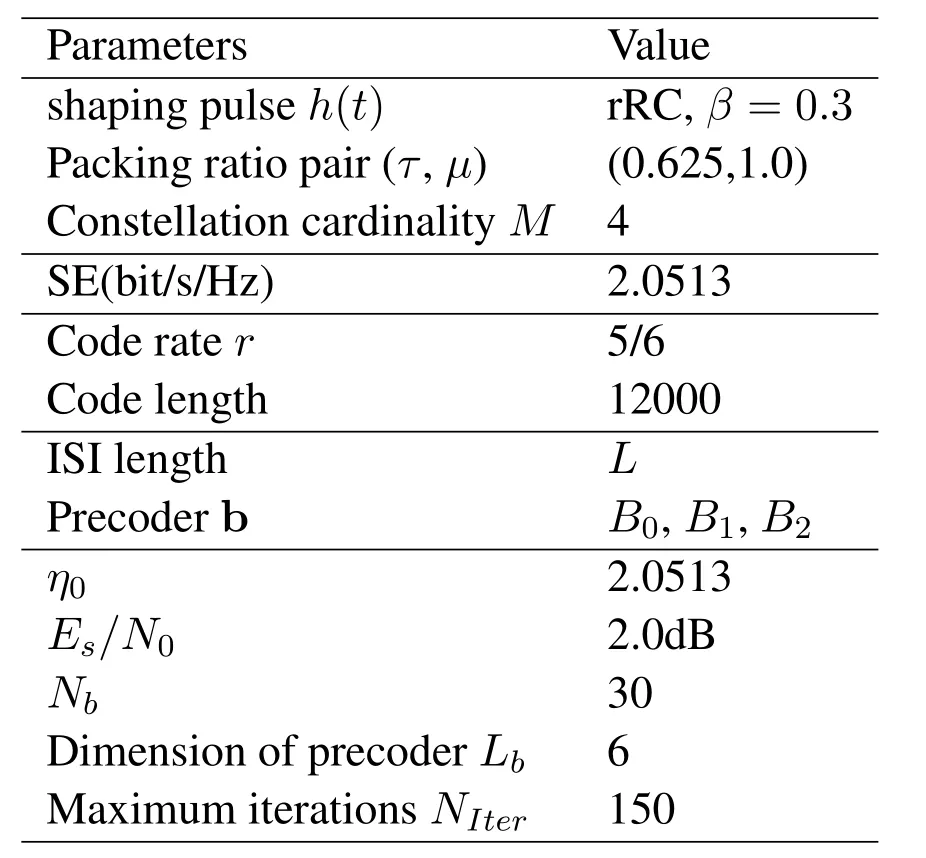
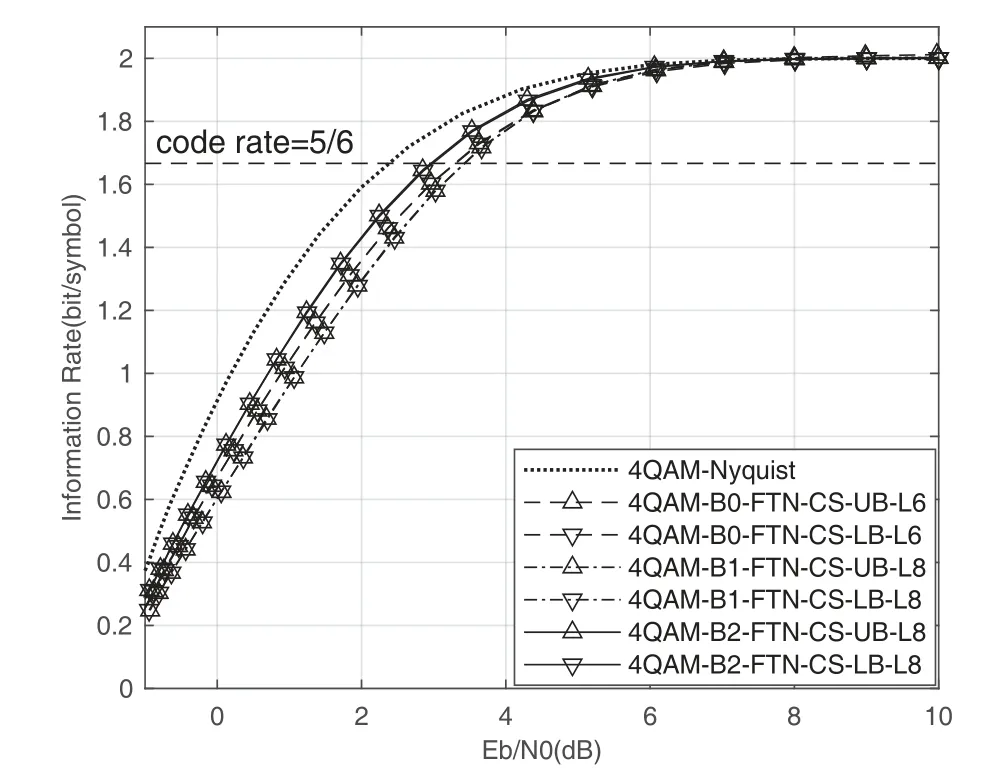
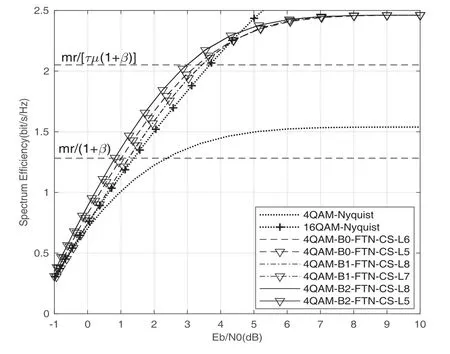
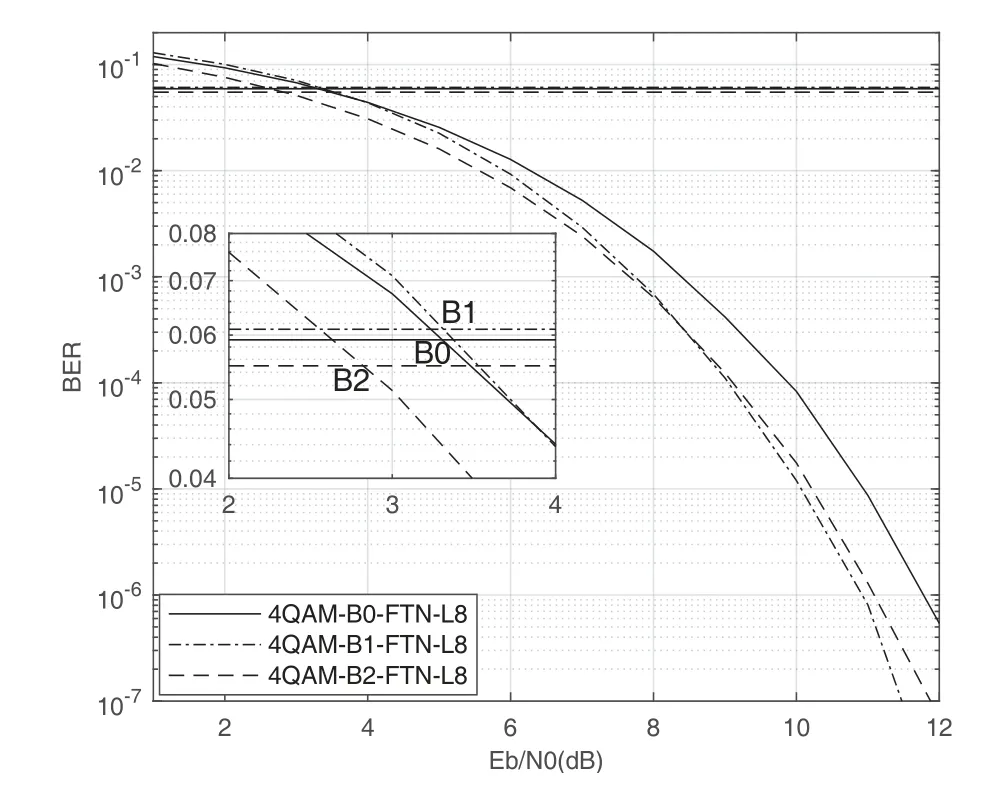
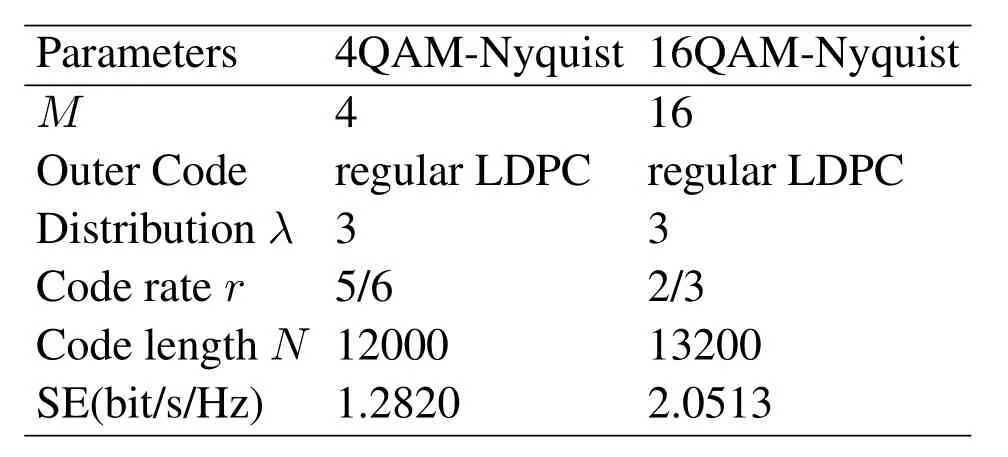
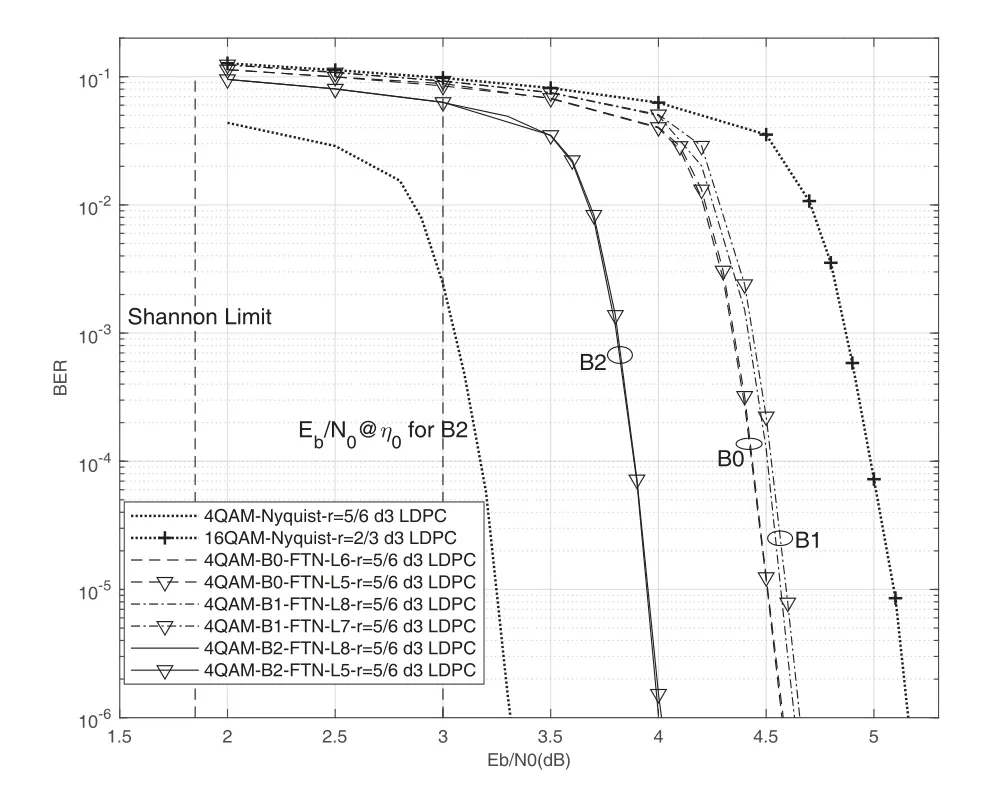
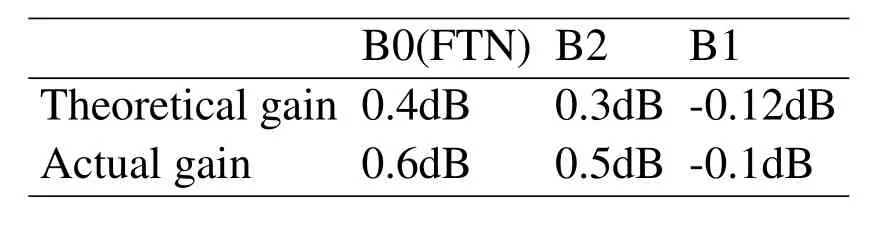
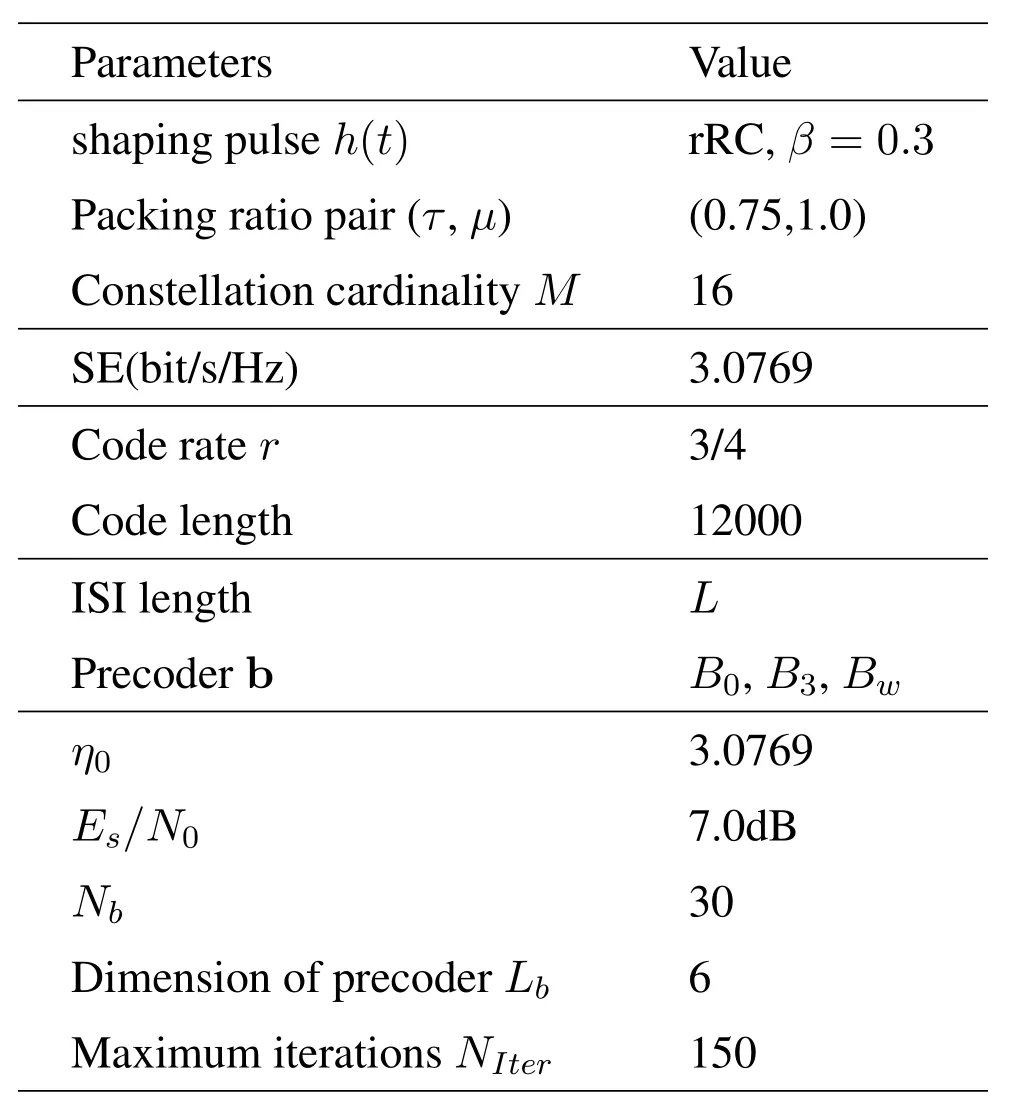
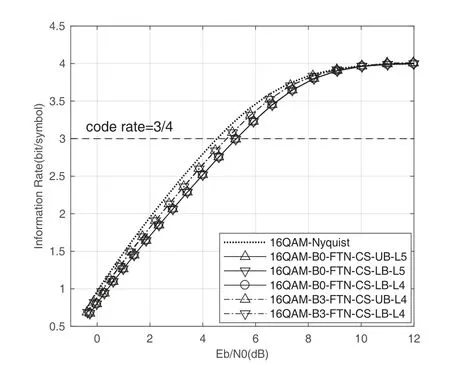
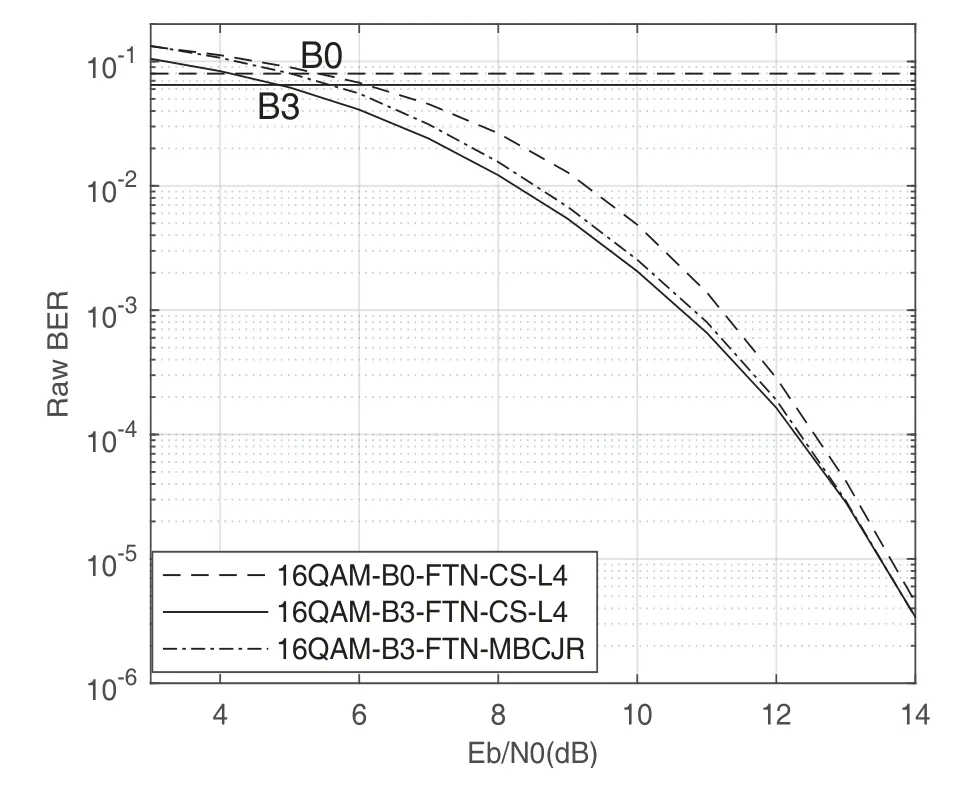
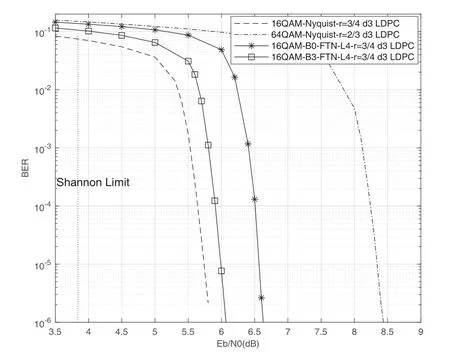
law where (·)∗stands for conjugate,gr=[gr0,gr1,···grL]hasL+1 taps,Lis the ISI length,zkis the output of the the front-end-filter,ykis the sampled value in y,Hrand Grare convolutional matrices corresponding to hrand gr[43],respectively.It should be noted that hrand grare revised by the precoder b[28].The original Ungerboeck BCJR algorithm hasLI+1 taps,whereLI=2[ζ/τ]+Lband[·]represents rounded down operator.The mismatched CSBCJR algorithm can reduce complexity whenL As shown in figure 1,the transmitter can be seen as a serially concatenated code (SCC) [50]which consists of the cascade of an inner code and outer code.The channel encoder severs as outer code.The cascade of the signal mapper,precoder and FTN modulator servers as inner code.The LLR values are passed between the FTN equalizer and LDPC decoder.After several iterations,a sequence ˆu can be found,which is regarded as the estimate of u. On the one hand,the shaping pulse is usually truncated(compressed)in the time domain.From the time scaling property,the compression in the time domain is equivalent to the expansion in the frequency domain.Thus,the absolute bandwidth of time-truncation rRC used in signal carrier FTN [25]is greater thanW.Most single carrier FTNs employWas their bandwidth to evaluate spectral efficiency and ignore the out-of-band expansion.To some extent,this evaluation method for single carrier FTN is insufficient.On the other hand,precoding an FTN signal may significantly alter and broaden its transmission spectrum[27].Therefore,we plan to employ a multicarrier FTN transmission at the beginning.When the number of carriers is large enough for multi-carrier FTN,the SE for this CM-FTN with a vanishing BER(such as 10−6) wherem·r(bit/symbol)is the maximum IR for the CM system with vanishing probability of error,andTsFcis the time-frequency resource occupied by each FTN symbol.Multi-carrier CM-FTN uses carrier spacingFcinstead of the bandwidthWto calculate SE.For a fair comparison with single-carrier precoded FTN in[25],we setFc=Win multi-carrier precoded FTN.Unlike single-carrier FTN,multi-carrier still has intercarrier interference (ICI) even ifFc=W.Multicarrier FTN is more sufficient than single-carrier FTN.The single-carrier detection [46]is employed at the receiver side.A single-carrier receiver can tolerate a small amount of inter-carrier interference (ICI).Each carrier employs the same signal processing procedure and has the approximate IR as well as BER performance.Because each carrier has the approximate performance,for convenience we replace the multicarrier FTN with the 3-carriers FTN which also considers the ICI. AsNm →∞,the per carrier information rate (IR)[11]supported by the FTN system can be expressed as whereEY(·)denotes the expectation operator with respect to the random variable Y,P(y/x)is the original channel law, and it can be computed by means of the simulationbased algorithm (SBA),i.e.,the forward recursion of the BCJR algorithm[11].The problem of computingP(y)is that the state spaces for the FTN channel are too large.The SBA works on a trellis withMLstates per time index,which becomes computationally unmanageable for large values ofMandL.So,we need to resort to bounds.Upper and lower bounds on the IRI(X;Y)[11][13]can be computed as follows It can also be computed through the SBA. From (11)to (15),we can find thatILB=IUB ⇔(y/x)=P(y/x)⇔IUB=I(X;Y) &ILB=I(X;Y).The law of the auxiliary channel in[13]and[43]does not considerγ2and is equivalent to ˜T(y/x)in this paper.The law ˜T(y/x) does not qualify as a valid conditional PDF.The law of the auxiliary channel is a significant quantity for the tightness of the upper and lower bounds.Unlike [43],this paper employs (7)as the law of the auxiliary channel to making the upper and lower bounds tighter and giving the IRis the smallestL,which yields the true information rate up to the accuracy of the plot. ForM-ary input,an optimization algorithm,which searching for the precoder b with IR or SE criterion to design an optimized FTN transmission filter,is introduced in this section. The lower boundILBon theI(X;Y)is achievable by a maximum-likelihood decoder for the auxiliary channel[11][13][43].ILBis a function of precoder b and ISI lengthLin this paper.The spectral efficiency(SE) for FTN system withM-ary input symbols can be expressed as whereηMFTNis the function of the precoder b andL.The larger theL,the tighter the upper and lower bounds,and the higher the computational complexity. By maximizing the SE in (16),the BB-PSO algorithm can help us find a precoder b good enough for CM-FTN based on CS and this can be described as follows, where the precoder b is the part ofφ(t) in (5) andLis a fixed value during the search.There is a trade off between the precision and computational complexity forL.The input sequence x isM-ary symbol sequence instead of Gaussian sequence.The values of precoder b can be seen as the particle positions andηMFTN(b,L)is the fitness function.The BB-PSO swarm hasNbparticles.The topologies structure{Ti} ≡{T1,T2,···,TNb}and Tirepresents local or global neighborhood topologies for thei-th particle.piis the previously best position(precoder)found by thei-th particle up to the current iteration,labeledk.giis the best neighbor fori-th particle in Ti.bi,piand giareLb-dimensional vectors with the componentsbij,pijandgij,j=0,1,···,Lb −1.The update rule for BB-PSO with Gaussian distribution is given as follows[33] whereN(,) represents the Gaussian distribution with mean (pij(k)+gij(k))/2 and standard deviation|pij(k)−gij(k)|.To find the optimal precoder,each particle moves in the direction to its previous best position piand local optimal giin the swarm. In this paper,the topologies structure{Ti}is the ring,which is suggested by Kennedy in [35].In the ring topology structure,a particle communicates with two of its neighbors using a ring topology.The main steps of BB-PSO searching the precoder for the FTN system are listed as follows[26]. Step 1.Determine the parameters of FTN system employing a CS detector for evaluating spectral efficiency,such asM,h(t),τ,µ,ISI lengthL,Es/N0,Nband the maximum spectral efficiencyη0atEs/N0. Step 2.Randomly initialize the swarm{bi}and biis the precoder. Step 3.Generate the ring topology{Ti}according to swarm sizeNb.For each particlei,initialize pi=biand Step 4.For each pair of piand gi,calculate its new position vector biaccording to (18). Step 5.For each particlei,evaluate the fitness function(bi,φ(t))in (16).And then set pi=biif(bi,L)(pi,L). Step 6.For each particlei,gi= pj∈Ti,bj∈Ti. Step 7.The global best position Step 8.IfηMFTN(gb,L)≥η0,then stop the algorithm and output the results gb andηMFTN(gb,L);otherwise go to Step 4 until a maximum number of iterationsNIteris reached. For coded modulation FTN with iterative decoding,the equalization complexity per iteration isO(ML)and the iterations increase computational complexity several times.For the CM-FTN with a largerL,the original BCJR algorithm detection becomes unmanageable due to high-complexity.The CS can reduce the ISI lengthLfor the FTN equalizer (BCJR detector).However,how to determine the value ofLfor CS has not been studied in the relevant literature.In this paper,we minimize the ISI lengthL=for CS such that The lower boundILBon theI(X;Y) is achievable by a maximum-likelihood decoder and the CS-BCJR decoder based onhas the lowest complexity without performance loss.This optimization can offer satisfactory performance with reasonable complexity for CM-FTN. Table1.Parameters for 4QAM-FTN. Figure2.Information rate for 4QAM-FTN-C0 and 4QAMNyquist.The FTN system without precoder is denoted as B0.The optimized precoders for the CM-FTN based on MED and IR criterion are denoted as B1 and B2,respectively. 4.1.1 Theoretical analysis The parameters for low order (4QAM) FTN system and BB-PSO algorithm are listed in Table1.In this paper,a set of parameters is selected from Table2 in [25],such as shaping pulseh(t),packing ratioτand dimension of precoderLb.Figure2 shows the results for the suggested boundsILBandIUBgenerated by using SBA based on CS and for the CM-AMI of 4QAM-Nyquist.It should be pointed out that B0-FTN is the benchmark for precoder optimization in this paper.This paper focuses on the optimization of precoderB2andLfor CM-FTN.The CS bounds withL=6 yield the true information rateI(X;Y) up to the accuracy of the plot[11].The bounds generated by using a truncated Ungerboeck receiver(TrU)[13]are also shown in Figure2.The TrU bounds need a larger ISI lengthL(L=7)to yield the true IR up to the accuracy of the plot.The simple truncation may minimize the channel mismatch [13]but it needs a larger ISI lengthLto yield the true information rate.Compared with TrU method,the CS method can use a smaller ISI lengthLto making the upper and lower bounds tighter and giving the true IRI(X;Y).=6 for 4QAM-B0-FTN based on CS.This paper focuses on the CM-FTN,where the code rateris usually less than 1.The 4QAM-B0-FTN has 0.9dB loss compared to the 4QAM-Nyquist at IR=1.67bit/symbol (r=5/6).The precoder can help the CM-FTN system to reduce this loss to the Nyquist system with the same code rater. Table2. for 4QAM-FTN with precoder. Table2. for 4QAM-FTN with precoder. note:B1=[-0.730270 0.600866-0.306958 0.009961-0.099239-0.038660]B2=[0.071940-0.216892 0.083173-0.810880 0.500629-0.180853] ? The 4QAM-FTN with B0 achieves the SE=2.0513bis/s/Hz (IR=1.67bit/symbol) atEs/N0=2.5dB.The precoder B2 can achieve precoding gain compared with B0 when the 4QAMB2-FTN achieves the same SE at lowerEs/N0,such as 2 .0dB in Table1.The BB-PSO algorithm is employed to find the optimal precoder for the CM-FTN system.The global best position gb is considered as the preco der B2.A largerLvalue can result in a more accurate IR value,but the corresponding complexity is also higher.There is a trade-off between ac curacy and computational efficiency in practice.Consideringiklm, 4QAM-B0-FTN,L=6 is a reasonable reference value for 4QAM-FTN in the precoder search process.The precoder B1 can help the 4QAM-FTN-B1 achieve the maximum MED[25].The MEDs for 4QAM-FTN system with different precoders are listed in Table2.The true information rateI(X;Y)for 4QAM-FTN with different precoder are shown in Figure3.for 4QAM-FTN with the precoder B0,B1 and B2 are 6,8 and 8,respectively.Compared with the 4QAM-B0-FTN,4QAM-B2-FTN has a 0.3dB precoding gain when the code rateris 5/6.Compared with the 4QAM-B1-FTN,4QAM-B2-FTN has a 0.42dB gain when the code rateris 5/6.It can be seen that the gap between the 4QAM-Nyquist and 4QAM-FTN can be reduced by the aid of precoder B2.Surprisingly,4QAM-B1-FTN has a 0.12dB loss compared with 4QAM-B0-FTN even if the MED of the 4QAM-B1-FTN is larger than that of the 4QAM-B0-FTN.The MED and IR cannot be harmonious in the FTN system.It can be seen that the IR is a more robust metric for error performance compared to MED in the following BER simulation.This situation also exists in the Nyquist system[14]. Figure3.Information rate for 4QAM-FTN with different precoder. We can find a minimum ISI lengthfor CS such thathas a little loss compared with the SEI(X;Y)/[τµ(1+β)].The SE of 4QAM-FTN withis shown in Figure4.4QAM-FTN-CS withhas a little loss compared with 4QAMFTN-CS withbut the computational complexity is greatly reduced.For the QAM-FTN,their realand complex-valued parts can be detected dependently or independently.If their real- and complex-valued parts are detected independently,the complexity can be further reduced and the calculation complexity isThe reduced complexity for 4QAMFTN-CS withare listed in Table3.L=for the FTN equalizer in (9). Figure4.SE of 4QAM-FTN-CS with Table3.Reduced complexity for 4QAM-FTN-CS with Table3.Reduced complexity for 4QAM-FTN-CS with ? As shown in Figure4,the SE of CM-Nyquist with a vanishing BER ismr/(1+β) and SE of CMFTN with a vanishing BER ismr/[τµ(1+β)].The maximum SE of 4QAM-Nyquist is 1.5385bit/s/Hz(r=1),which is less than SE of CM-4QAM-FTN(SE=2.0513bit/s/Hz,r=5/6)in this paper.16QAMNyquist is employed here and it can achieve the same SE as CM-4QAM-FTN(2.0513bit/s/Hz).4QAM-B0-FTN with=5 has a 0.4dB FTN gain compared to 16QAM-Nyquist at same SE.4QAM-B2-FTN with=5 has a 0.3dB precoding gain compared with 4QAM-B0-FTN with=5 at the same SE.It should be noted that the SE of 4QAM-Nyquist is less than that of 4QAM-FTN at the same code rater. 4.1.2 Monte-carlo simulation Figure5.Raw BER for uncoded 4QAM-FTN based on CS. Table4.Simulation parameters for CM-Nyquist. TherawBER for 4QAM-FTN is shown in Figure5.4QAM-B1-FTN has the largestd2minand it has the lowestrawBER atEb/N0=11dB;4QAM-B0-FTN has the smallestd2minand it has the highestrawBER atEb/N0=11dB.This result confirms that a larger MEDd2minleads to a betterrawBER performance at high SNR.4QAM-B1-FTN has the largestd2minbut it has the highestrawBER atEb/N0=3dB.The largest MEDd2mincannot lead to the lowestrawBER at low SNR.4QAM-B0-FTN has the smallestd2minbut it has not the highestrawBER atEb/N0=3dB.The MEDd2mincan’t tell us reliable information of FTN at the low SNR.TherawBER of the CM-FTN at an operating point generally corresponds to the low SNR region,which will be confirmed below.The MED has a noncritical effect onrawBER at low SNR and has a critical impact on rawBERat high SNR.This results in the intersection between B1 and B2 in Fig.5.The MEDd2minis not a robust performance metric for the CM-FTN. In order to confirm the effectiveness of the optimization method proposed,we compare the BER performance of the optimized 4QAM-FTN with the 16QAM-Nyquist and 4QAM-Nyquist.16QAM-Nyquist has the same SE as the 4QAM-FTN.4QAMNyquist has the same outer code as the 4QAM-FTN.The parameters for CM-4QAM-Nyquist and CM-16QAM-Nyquist are listed in Table4.Here,the rate-5/6 regular LDPC code is employed for 4QAM-FTN and 4QAM-Nyquist and its average column degree is 3,abbreviatedr=5/6 d3 LDPC.The parameters for CM-4QAM-FTN are listed in Table1.The number of local iteration(LDPC iteration)is limited to 30 and the number of global iteration (turbo iteration) is limited to 5.Figure6 shows the BER performances of CM-4QAM-FTN,CM-4QAM-Nyquist and CM-16QAMNyquist.The CM-4QAM-B0/B1/B2-FTN withhas approximately same BER performance as the CM-4QAM-B0/B1/B2-FTN withThis confirms that CS optimization based on the IR criterion is effective.The CS decoder based onhas the lowest complexity with a little BER performance loss. CM-4QAM-B0-FTN has a nearly 0.6dB FTN gain compared to CM-16QAM-Nyquist at BER=10−6.The FTN gain is close to the theoretical gain(0.4dB).CM-4QAM-B2-FTN has a nearly 0.5dB precoding gain compared with CM-4QAM-B0-FTN at BER=10−6.The precoding gain is close to the theoretical gain(0.3dB).The gap between CM-4QAM-Nyquist and CM-4QAM-B2-FTN is only 0.65dB.The BER gap is close to the theoretical gap (0.6dB).CM-4QAM-B1-FTN has a nearly 0.1dB precoding loss compared with CM-4QAM-B0-FTN at BER=10−6.The precoding loss is close to the theoretical loss (0.12dB).A large MED cannot guarantee a better BER performance and better IR performance produces a better BER performance.These gains and losses are summarized in Table5. The CM-FTN achieves the BER=10−6at the operating point.RawBER=5.92×10−2for CM-4QAMB0-FTN at the operating point;rawBER=6.2×10−2for CM-4QAM-B1-FTN at the operating point;rawBER=5.7×10−2for CM-4QAM-B2-FTN at the operating point;TheserawBERs are represented by the intersection points B0,B1 and B2 in Figure5.It can be seen that therawBER of the CM-FTN at the operating point generally corresponds to the low SNR region in Figure5.The intersection B2 in FigureRaw-BER4QAM has a 0.5dB gain compared with intersection B0;the intersection B1 has a 0.1dB loss compared with intersection B0.TherawBER results in the low SNR region are consistent with the previous BER results.Precoder can enhance the performance of CMFTN because it improves therawBER of FTN system at low SNR.However,the MEDd2mincan’t tell us reliable information about therawBER of FTN at the low SNR.This paper uses IR or SE as a performance metric for the CM-FTN system rather than the MED. Figure6.BER performance of 4QAM-FTN,4QAM-Nyquist and 16QAM-Nyquist. Table5.Gain and loss for 4QAM-FTN. As with the previous analysis method,we first optimize the precoder for high order FTN by BB-PSO algorithm.Then we optimizefor the high order FTN with/without precoder according to the criteria,theILBclose to theI(X;Y).The FTN-CS withto yield the true IRI(X;Y).The FTN-CS withcan reduce the complexity without BER performance loss. 4.2.1 Theoretical analysis A set of parameters for high order (16QAM) FTN is selected from Table6 in [25],such as shaping pulseh(t)and packing ratioτ.The parameters for 16QAMFTN system and BB-PSO algorithm are listed in Table1.16QAM-FTN with B0/B3/Bw has the same MED as shown in Table7.Their MEDs reach a maximum of 0.8.There is no need for precoding optimization based on the MED criterion.Figure7 shows the true information rateI(X;Y)for 16QAM-FTN with/without precoder.16QAM-B3-FTN has a 0.4dB precoding gain compared with the 16QAM-B0-FTN at thecode rater=3/4,even if they have the same MED.16QAM-B3-FTN reduces the gap between 16QAMNyquist and 16QAM-B0-FTN from 0.8dB to 0.4dB at the same code rate.andfor 16QAMB0-FTN-CS;andfor 16QAM-B3-FTN-CS.Consideringin the benchmark 16QAM-B0-FTN,L=5 is a reasonable reference value for 16QAM-FTN-CS in the precoder search process. Table6.Parameters for 16QAM-FTN. Table7. for 16QAM-FTN with precoder. Table7. for 16QAM-FTN with precoder. note:The FTN system without precoder is denoted as B0.B3 is the optimized precoders for the CM-16QAM-FTN by IR criterion.Bw is the waterfilling filter [28]for CM-16QAM-FTN.B3=[0.3445 0.1484 0.4833 -0.6526 0.4176-0.1592]. ? The SE of CM-Nyquist with a vanishing BER ismr/(1+β) and SE of CM-FTN with a vanishing BER ismr/[τµ(1+β)]as shown in Figure8.The maximum SE of 16QAM-Nyquist is 3.0769bit/s/Hz(r=1),which equals SE of CM-16QAM-FTN(SE=3.0769bit/s/Hz,r=3/4)in this paper.However,it is difficult to construct an LDPC code withr=1.64QAM-Nyquist is employed here,which can achieve the same SE as CM-16QAM-FTN (3.0769bit/s/Hz).16QAM-B0-FTN with=4 has a 1.4dB FTN gain compared to 64QAM-Nyquist at same SE.16QAMBw-FTN with=4 has a 0.1dB loss compared with 16QAM-B0-FTN with=4 at the same SE.There is no precoding gain for 16QAM-Bw-FTN. Figure7.Information rate for 16QAM-FTN with different precoder. Figure8.SE of 16QAM-FTN-CS with 4.2.2 Monte-carlo simulation Figure9.Raw BER for uncoded 16QAM-FTN based on CS. Table8.Simulation parameters for CM-Nyquist. Figure10.BER performance of 16QAM-FTN,16QAMNyquist and 64QAM-Nyquist. TherawBER for 16QAM-FTN is shown in Figure9.Due to the same MED,both FTNs have approximately equalrawBER performance at the high SNR region,such asEb/N0=14dB.However,theirrawBER performance is quite different in the low SNR region,such asEb/N0=6dB.The MEDd2mincan’t tell us reliable information of the FTN at the low SNR.The MEDd2minis not a robust performance metric for the higher-order CM-FTN.We compare the performance of 16QAM-B3-FTN using the CS technique and the MBCJR method in [40].M=32 [25]for the MBCJR algorithm.TherawBER performance of the MBCJR algorithm is worse than that of the CS algorithm at the low SNR region.The two algorithms have approximately equalrawBER performance at the high SNR region.The MBCJR often leads to low quality of softoutput at low SNR.This is not good for the iterative system,so this paper considers the optimization of the CS algorithm. We compare the BER performance of the optimized CM-16QAM-FTN with the CM-64QAM-Nyquist and CM-16QAM-Nyquist in Figure10.The parameters for CM-16QAM-Nyquist and CM-64QAM-Nyquist are listed in Table8.The rate-3/4 regular LDPC code is employed for 16QAM-FTN and 16QAM-Nyquist and its average column degree is 3,abbreviatedr=3/4 d3 LDPC.The number of local iteration is limited to 30 and the number of global iteration is limited to 5.The ISI length for FTN equalizer is CM-16QAM-B0-FTN has a nearly 1.8dB FTN gain compared to CM-64QAM-Nyquist at BER=10−6.CM-16QAM-B3-FTN has a nearly 0.6dB precoding gain compared with CM-16QAM-B0-FTN at BER=10−6.The precoding gain is close to the theoretical gain(0.4dB).The gap between CM-16QAMNyquist and CM-16QAM-B3-FTN is only 0.3dB.The BER gap is close to the theoretical gap(0.4dB).These gains are summarized in Table9. RawBER=7.99×10−2for CM-16QAM-B0-FTN at the operating point;rawBER=6.48×10−2for CM-16QAM-B3-FTN at the operating point.TheserawBERs are represented by the intersection points B0,B3 in Figure9.It can be seen that therawBER of the high order CM-FTN at the operating point generally corresponds to the low SNR region in Figure9.The intersection B3 in Figure9 has a 0.6dB gain compared with the intersection B0.ThisrawBER results in the low SNR region are consistent with the BER results.This result again confirms that IR or SE is a better performance metric for the CM-FTN system than the MED.The MEDd2minis not robust especially forrawBER performance in the low SNR region. TheserawBER and BER results are agreement with the theoretical analysis and confirm that the optimization method can provide a satisfactory performance improvement. Table9.Gain for 16QAM-FTN. In this paper,we investigated a coded modulation FTN(CM-FTN) transmission scheme with joint optimization of precoder and channel shortening to improve BER performance and reduce the complexity of FTN equalizer.Our study identified that IR or SE is a better performance metric for the CM-FTN system than the MED.Unlike[43],this paper employed (7)as the law of the auxiliary channel to making the upper and lower bounds tighter and giving the IRI(X;Y).We optimized the precoder of CM-FTN based on maximizing the SE criterion by using the BB-PSO algorithm.Then,we optimizedfor CM-FTN with-/without precoder according to the criterion that theILBis close to theI(X;Y) and FTN equalizer acceptsas the minimum ISI length without performance loss.We verified our proposals by Monte-Carlo BER simulations to demonstrate the performance gain of the joint optimization for the CM-FTN.The precoding gain for 16QAM-FTN(4QAM-FTN)is 0.6dB(0.5dB)atBER=10−6and it is close to the theoretical gain based on the IR criterion.The BER gain at the operating point and therawBER gain in the low SNR region are consistent with the theoretical analysis.A maximum of 87.5%of the complexity of FTN equalizer is reduced,and there is no BER loss.Our contributions in this paper can be extended to other ISI channels and scenarios. ACKNOWLEDGEMENT This work was supported by National Natural Science Foundation of China(No.61961014).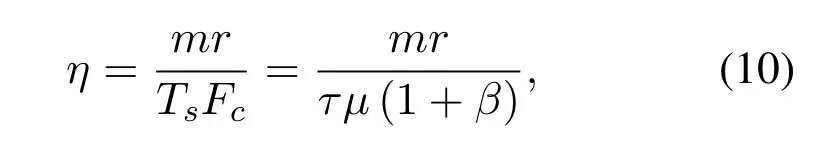
III.PRECODER AND CHANNEL SHORTENING OPTIMIZATION BASED ON IR CRITERION
3.1 Information Rate Criterion
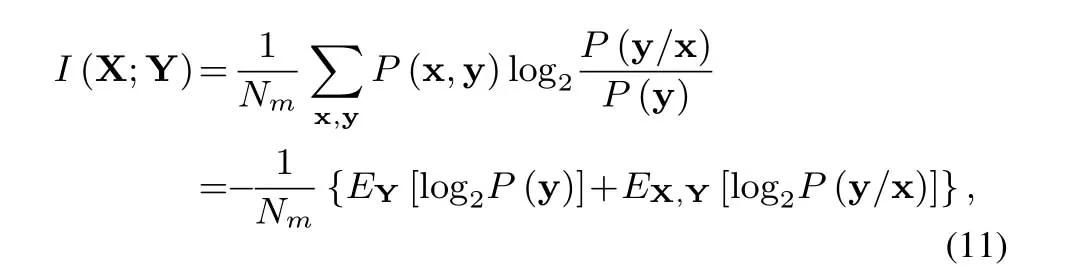
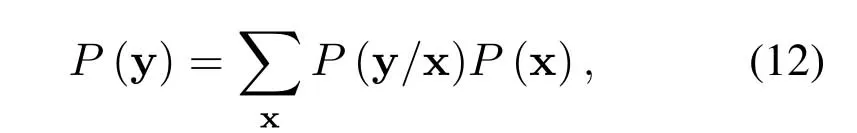

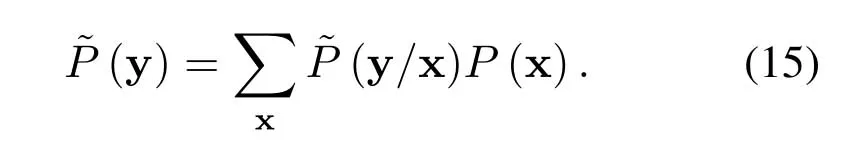
3.2 Precoder Optimization Based on IR Criterion
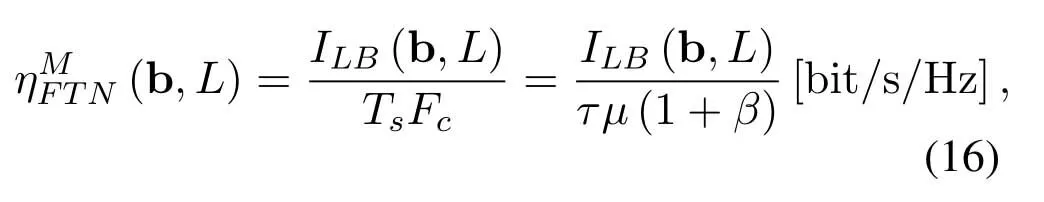

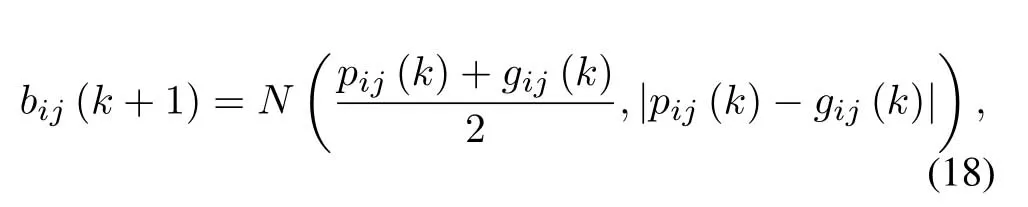
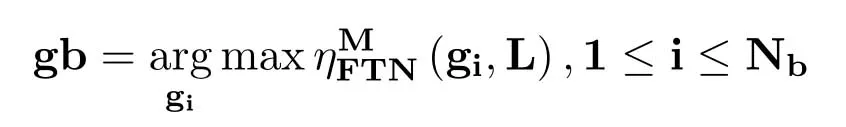
3.3 CS Optimization Based on IR Criterion
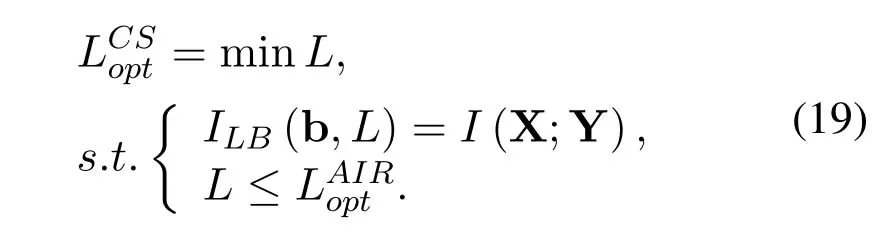
IV.RESULTS
4.1 Case 1:Low Order FTN

4.2 Case 2:High Order FTN




V.CONCLUSION
- China Communications的其它文章
- Future 5G-Oriented System for Urban Rail Transit:Opportunities and Challenges
- Multi-Stage Hierarchical Channel Allocation in UAV-Assisted D2D Networks:A Stackelberg Game Approach
- Performance Analysis of Uplink Massive Spatial Modulation MIMO Systems in Transmit-Correlated Rayleigh Channels
- Development of Hybrid ARQ Protocol for the Quantum Communication System on Stabilizer Codes
- Analysis and Design of Scheduling Schemes for Wireless Networks with Unsaturated Traffic
- A Survey on Routing Algorithms for Opportunistic Mobile Social Networks

