An Efficient Trajectory Planning for Cellular-Connected UAV under the Connectivity Constraint
Dingcheng Yang,Qian Dan,Lin Xiao,*,Chuankuan Liu,Laurie Cuthbert
1 School of Information Engineering,Nanchang University,Nanchang 330031,China
2 School of Computer Science,Jiangxi University of Traditional Chinese Medicine,Nanchang 330004,China
3 Information Systems Research Centre,Macao Polytechnic Institute,Macao,China
Abstract:Unmanned Aerial Vehicles (UAVs) acting as aerial users to access the cellular network form a promising solution to guarantee its safe and efficient operations via the high-quality communication.Due to the flexible mobility of UAVs and the coverage range limits of ground base station(GBS),the signalto-noise ratio (SNR) of the communication link between UAVs and GBS will fluctuate.It is an important requirement to maintain the UAV’s cellular connection to meet a certain SNR requirement during the mission for UAV flying from take off to landing.In this paper,we study an efficient trajectory planning method that can minimize a cellular-connected UAV’s mission completion time under the connectivity requirement.The conventional method to tackle this problem adopts graph theory or a dynamic programming method to optimize the trajectory,which generally incurs high computational complexities.Moreover,there is a nonnegligible performance gap compared to the optimal solution.To this end,we propose an iterative trajectory optimizing algorithm based on geometric planning.Firstly,we apply graph theory to obtain all the possible UAV-GBS association sequences and select the candidate association sequences based on the topological relationship among UAV and GBSs.Next,adopting the triangle inequality property,an iterative handover location design is proposed to determine the shortest flight trajectory with fast convergence and low computation complexity.Then,the best flight trajectory can be obtained by comparing all the candidate trajectories.Lastly,we revealed the tradeoff between mission completion time and flight energy consumption.Numerical results validate that our proposed solution can obtain the effectiveness with set accuracy and outperform against the benchmark schemes with affordable computation time.
Keywords:UAV communication;trajectory planning;cellular-connected UAV;connectivity requirement
I.INTRODUCTION
As Unmanned Aerial Vehicles (UAVs) have the cost effectiveness and outstanding capability to execute complex and dangerous tasks,the applications of UAVs have had a massive upsurge in recent years,in areas such as cargo delivery,aerial imaging,data collection,plant protection,and aerial base stations[1,2].In order to support these applications and ensure they are operated in a safe and controllable way,the critical control and command(C2)message should be exchanged between the UAV and ground pilot/controller via control and non-payload communication (CNPC)[3]with an ultra-reliable service;the data traffic for applications such as video streaming or sensor data should be high-quality delivered over the high-rate payload communication[4].
Wireless channel propagation models are roughly classified into two types:large-scale path loss models and small-scale fading models which is mainly divided into Rayleigh fading model and Rice fading model.In reality,large-scale loss models are widely being applied for multifarious substantial scenarios.In previous studies,the channel model between the UAV and the GBS can be classified into three categories:Spatial free model[5],field measurement model[6],and probabilistic LOS model[7].[8]investigated the challenges and the fundamental tradeoffs in UAV-enabled wireless network,and the authors also proposed potential benefits and applications of UAVs in wireless communications.[9,10]studies the UAV channel modeling and measure campaigns launched for UAV channel modeling,which helps extend the practical application of UAVs in multiple areas.To illustrate the most essential design insights and for ease of exposition,we adopt the line-of-sight propagation model to explain our algorithm ideas.The UAV communicated with the GBS by line-of-sight channel when the flying in rural and suburban environments.In practical applications,considering non-line-of-sight channels and other performance requirements will be left as our future work.
Traditional point-to-point UAV-ground communications over unlicensed spectrum would restrict the operational ranges of these applications to visual-lineof-sight(VLOS)range owing to the public safety and link quality constraints[11,12].The research community has proposed a new solution namedcellular −enabled UAV communicationto extend the operation range for UAV applications [13].Specifically,since mobile operators already have constructed the ground infrastructure with a ubiquitous coverage,it can be adapted to serve such air-to-ground link[14].Then,UAVs can act as aerial users to communicate with the ground base station in the cellular network [15],so enabling the UAV to operate in beyond-VLOS ranges[16].UAV −assisted cellular communicationis a UAV carry communication device that acts as an airborne mobile base station to enhance coverage of terrestrial cellular networks[17].UAV-BSs have wide applications in emergency communication,rescue and other fields[18].
Compared to terrestrial users in a cellular network,a cellular-connected UAV has more flexible mobility and a higher altitude operating environment,which bring both opportunities and challenges for the optimization of cellular-enabled UAV communication[19].In work of [20],the author summarized the challenges and research directions of mmWave-UAV communications.UAVs would fly above the vegetation,buildings and terrain elevations [21].The radio path between UAV and GBS is more likely to experience line-of-sight(LOS)propagations,which leads to macro-diversity gains,but also suffering sever interferences from surrounding GBSs [22].Non-orthogonal multiple access (NOMA) technique and deep learning methods have been used to investigate the interference management issues for Cellular-Connected UAVs [23].Combining mobile edge computing and cellular-connected UAV,the computation offloading to GBS and UAV trajectory optimization were studied in[24].Recently,many researchers focused on energy efficiency.In the work [25],the energy consumption model of different flight modes of UAVs is discussed.The work [26]considers the advantages of wireless power supply in two-way communication.The capacity of battery also be considered in airborne relay communication.Energy-efficient cooperative relaying scheme was adopted to extend network lifetime [27].In the work[28,29],the authors adopt solar panels to solve the problem of energy limitation of UAVs.
In the work of [30],the authors proposed a flight power model for fixed-wing UAVs and maximized the flight energy efficiency by optimizing the flight trajectory.While the authors in [31]studies a rotarywing UAV sends/collects data to/from multiple ground nodes (GNs),and minimize the energy consumption of UAV flight to meet the throughput requirements of each GN.In [32],it is proposed a cooperative UAV sense-and-send protocol to enable the UAV-to-X communications,and the optimal solution which is maximized the uplink sum-rate is investigated by formulating the subchannel allocation and optimizing UAV speed.In work [33],the UAV acts as an amplifyand-forward relay,and the trajectory and the transmit power of UAV is optimized by minimizing the outage probability of the relay network.While the authors in[34]investigate the scenario that one UAV jointly performs sensing tasks and data transmission to the single base station,the energy efficiency(EE)of the system is maximized by optimizing UAV sensing and transmission.
Considering the mission for a UAV is to fly from a starting location to a final location,it is an important issue to investigate the wireless connectivity between the cellular-connected UAV and its associated GBSs under a prescribed QoS requirement in terms of minimum SNR for data traffic[35].Considering the QoS requirement may not be satisfied for some of the flight time,[1]proposed a dynamic programming method to optimize the UAV trajectory with a constraint on outage duration:it can obtain a approximate solution with a higher computation complexity.[36]analyzed the trajectory optimization issue for a cellular-connected UAV maintaining the wireless connectivity with one of the GBSs at all time.Moreover,adopting graph theory and Lagrange relaxation method,the authors extended the solution to a scenario with an outage duration constraint in[37].The proposed algorithms in[37]should involve complex mathematical tools to resolve the optimization problem with high commutation complexity.
In this paper,we study the path planning schemes of cellular-connected UAVs with real-time connection limits to the cellular network.We adopt graph theory and geometric inequality to design an efficient trajectory planning algorithm.Firstly,Graph theory is adopted to obtain all the possible UAV-GBS association sequences based on the topological relationship between UAV and GBSs.Secondly,applying the triangle inequality property [38],the optimal handover point between two GBSs can be obtained by an iterative method with fast convergence and low computation complexity.Then,through comparing all the candidate trajectories,the shortest trajectory can be determined.Finally,we revealed the tradeoff between mission completion time and flight energy consumption.
The rest of the paper is organized as follows.Section II introduces the system model and problem formulation.In Section III,an efficient algorithm is proposed to design the optimal trajectory.In Section IV,numerical results are analyzed.Finally,conclusions are drawn in Section V.
II.SYSTEM MODEL
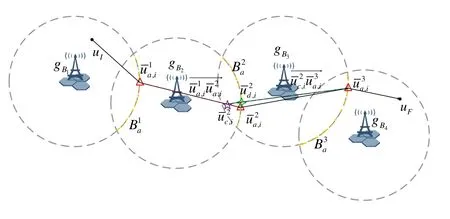
As shown in Figure1,we consider a cellularconnected UAV that is served byL ≥1 GBSs during the flight mission.Suppose that the cellular-connected UAV operates at a constant altitudeH.The cellularconnected UAV performs a flight mission from an initial locationLIto the final locationLFwith a constant speedV.The UAV must maintain its wireless connection performance with the one of the GBSs under the connectivity requirement during the flight mission[39].
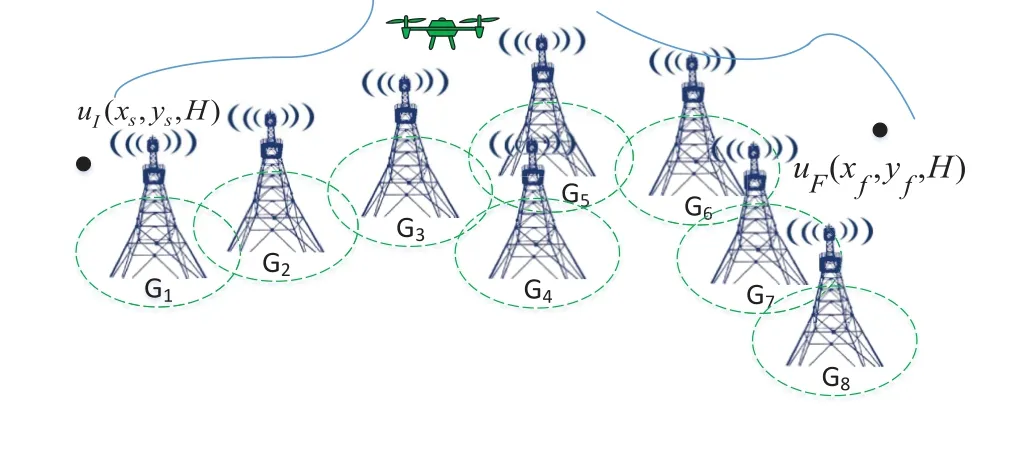
Figure1.Illustration of a cellular-connected UAV trajectory designing system.
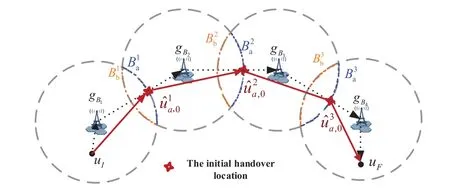
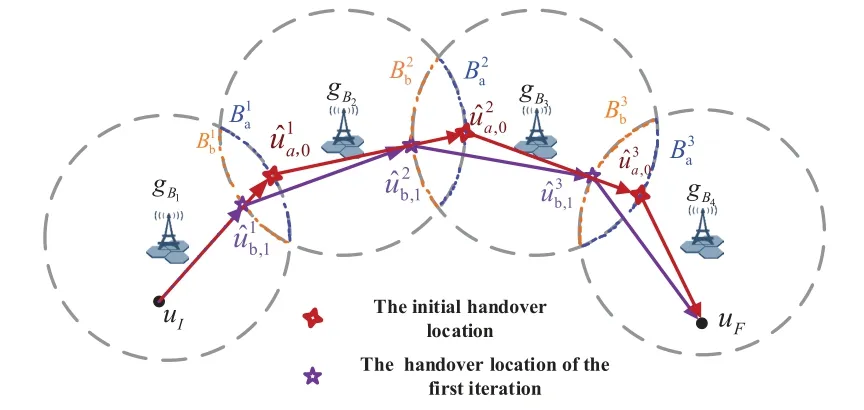
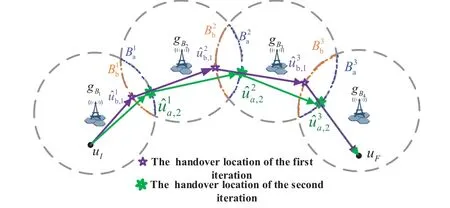
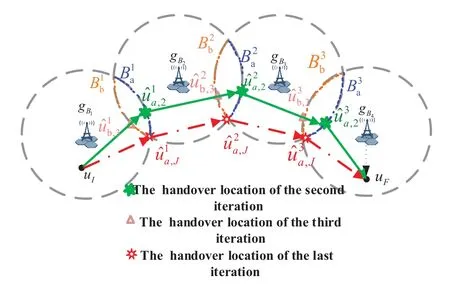
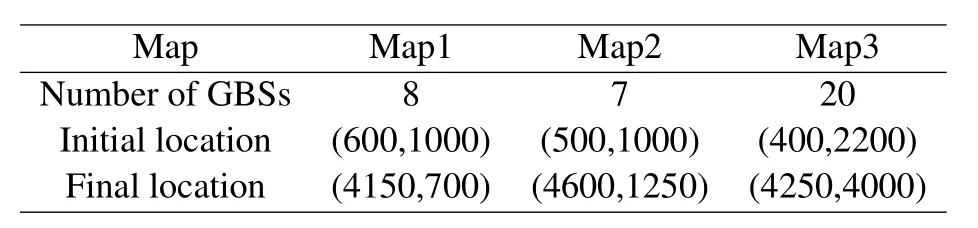
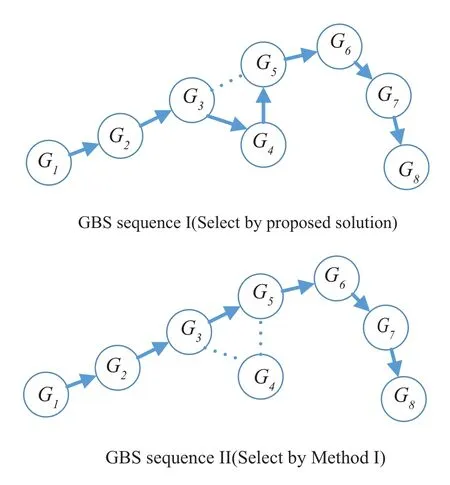
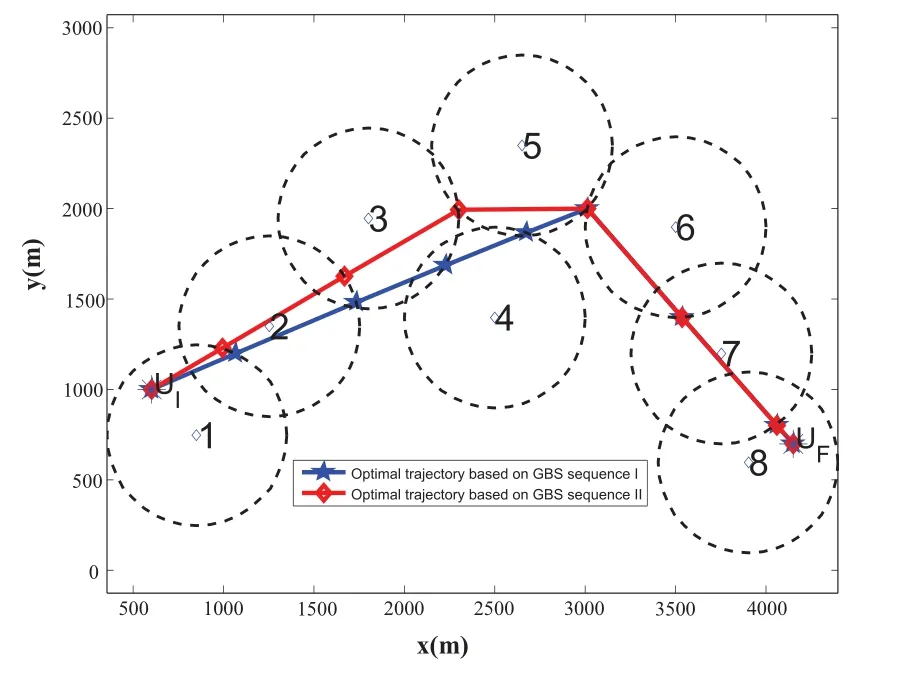
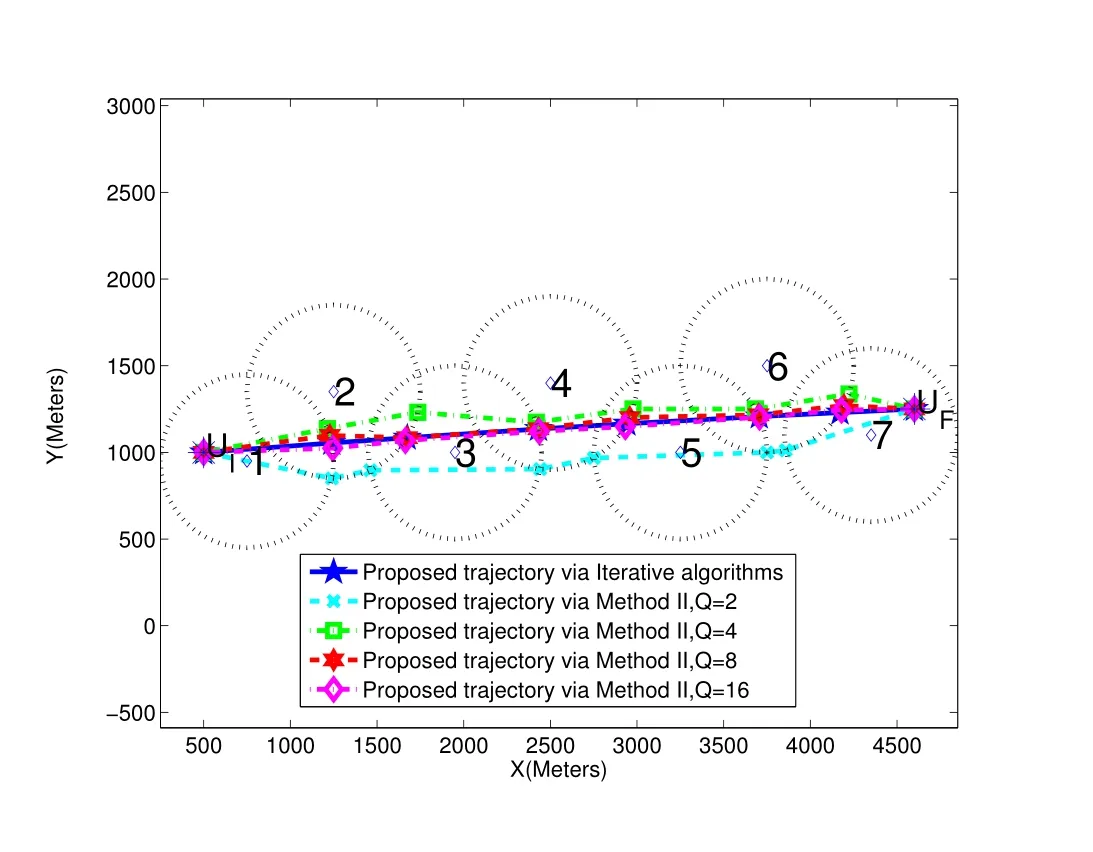
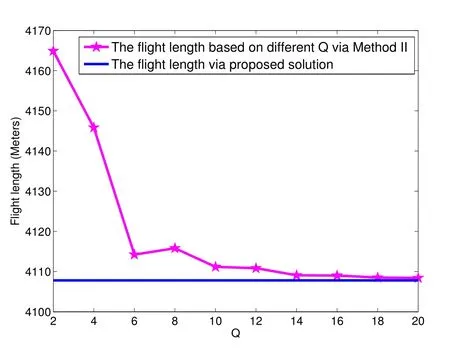
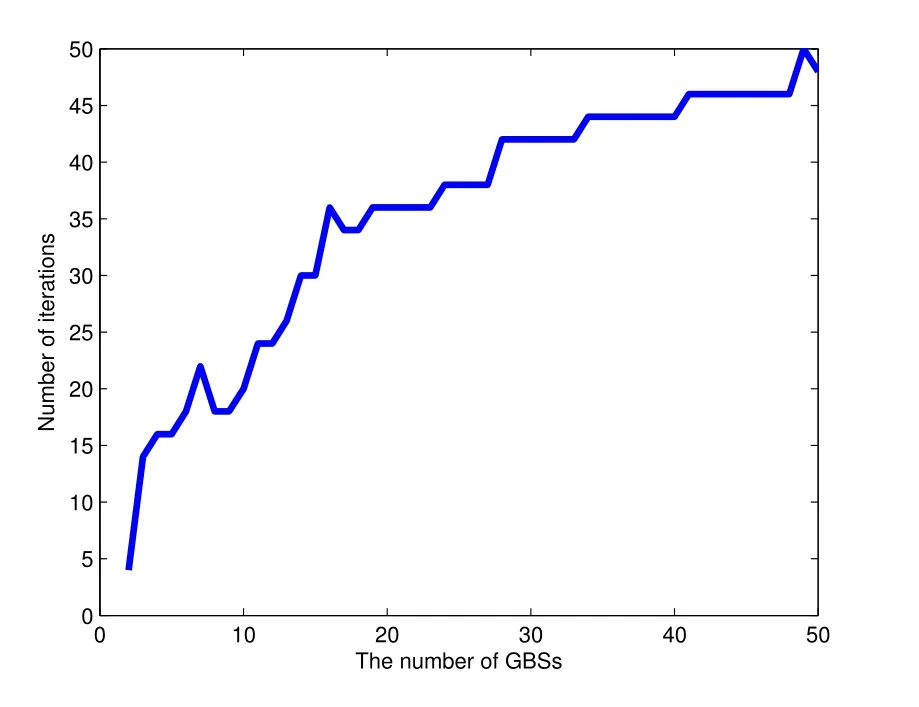
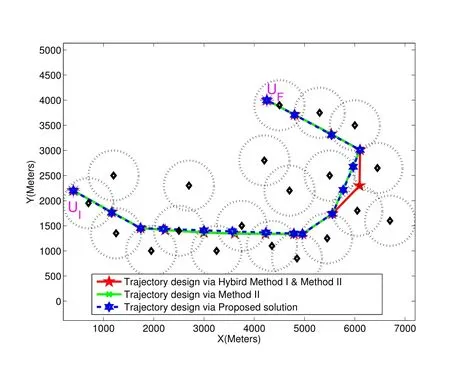
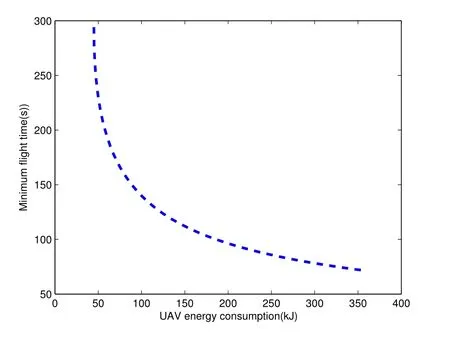
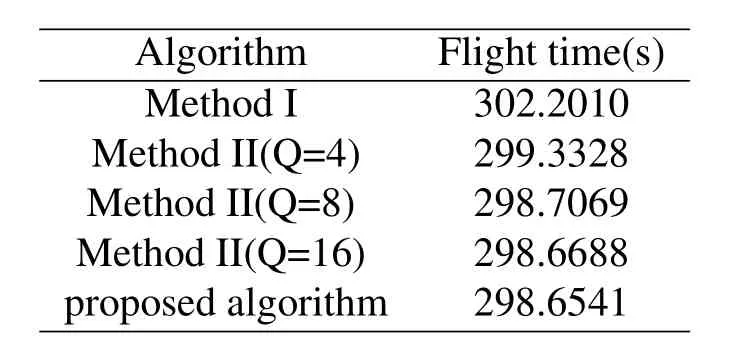
For ease of exposition,we assume that all antennas of the GBS are deposed at the same fixed height ofHgwithHg ≪ H.Consider a threedimensional (3D) Cartesian coordinate system such that thel −thGBS is located at (xl,yl,Hg),wherel ∈L={1,2,3,...L},Lis set ofLGBSs.We denoteLI(xI,yI,H) andLF(xF,yF,H) as the coordinates of the initial location and the final location,and the time-varying coordinate of the flying UAV can be denoted as(x(t),y(t),H),where 0 To illustrate the most essential design insights and for ease of exposition,we adopt the LoS communication model for the UAV-to-GBS/GBS-to-UAV links in this paper [16].This is a reasonable assumption for certain environment such as in rural area where there is little blockage and scattering,and/or when the UAV flies at sufficiently high altitude so that there is a high probability of clear LoS link with the GBS of interest[17].The time-varying channel coefficient between cellular UAV andl −thGBS can be expressed as: whereβ0denotes the channel power gain at the reference distance ofd0=1 m. Generally,there are two main data stream between the cellular UAV and the GBSs[40,41].The UAV uploads the collected information(such as image,video,or sensor data)to the base station.The GBSs send the command or information data from the server to the UAV.In practical implementations,in order to emphasize the real-time performance of information transmission and reception,assume that the receiver side of the cellular UAV needs a large signal-to-noise ratio[42].Therefore,the connectivity performance with QoS requirement between UAV and GBS would be an important issue for this scenario[43].When the UAV flies through multiple GBSs overlap areas,it would connect to the nearest base station to obtain the maximum signal-to-noise ratio.Consequently,the SNR at the cellular UAV can be written as In this paper,we adopt the receiver SNR of the UAV as the evaluation criterion of connectivity for the cellular-connected UAV communication.It is assumed thatsminis the minimum SNR requirement for the communication between the UAV and the GBSs.Therefore,the maximum horizontal distancedmaxbetween the cellular UAV and its closest GBS is: It is indicated that the SNR constraint of UAV’s QoS requirement can be equivalent to the location constraint on the horizontal distance between the cellular UAV and its closest GBS.In other words,the relationship between the actual distanced(t) from the UAV to its closest GBS and the thresholddmaxwould evaluate the cellular UAV’s connectivity performance.For the real-time QoS requirement scenario,the delaysensitive connectivity constraint should be maintained as follows: In this paper,we aim to minimize the UAV’s flight time from the starting location to the final position while maintaining the real-time connection between cellular UAV and GBSs.We denoteVmaxas UAV maximum flight speed.Then the UAV’s velocity constraint is‖˙u(t)‖ ≤Vmax,∀t ∈{0,T},where‖˙u(t)‖represents the UAV velocity.The UAV maintains realtime communication with the GBS during the flight.The signal-to-noise ratio is adopted to indicate the UAV communication service quality.The UAV only communicates with the nearest single GBS at each time during the flight.In order to meet the quality of communication services,the projection distance of the UAV from the GBSs at any time during the flight must be less thanR.The optimization problem can be formulated as: Note thatP1 is a non-convex optimization problem[44].It is difficult to directly solve it efficiently.We propose a two-step iterative algorithm based on graph theory and geometric inequality to find the efficient solution. Considering the cellular UAV’s connectivity constraint,the feasibility of the flight trajectory would be the first important issue to be checked[39].We adopt GBS-UAV association sequenceB=[B1,...,BN],whereBn ∈L[36]to indicate the order in which the GBS associates with the cellular UAV along the flight trajectory,e.g.the cellular UAV is first associated with GBSB1,then it hands over to GBSB2,etc.,There would be in totalNassociated GBSs along the UAV’s trajectory.The feasible GBS-UAV association sequence should satisfy the following conditions as mentioned in[36]: It is indicated that there is a disk region centered at the GBSglwith radiusdmaxon the horizontal plane,within which the UAV can communicate with the GBS while satisfying the QoS requirement.Furthermore,any two consecutive GBSs in the GBS-UAV association sequence should have an intersection area that can guarantee the UAV’s connectivity when the hand over operation occurred.Therefore,the feasibility of flight trajectory can be formulated as a graph connectivity problem.It is proposed to construct an undirected weighted graph denoted asG=(V,E),where the vertex setVis presented as: whereU0,UFdenote the cellular UAV’s initial/final locations,Glindicates thel −thGBS.The edge setEis formulated as: The weight of each edge can be given as: The feasibility issue of the flight trajectory can be reformulated as whether there is a path fromU0toUFin graphG.It can be solved efficiently by the classic algorithms of graph theory such as breadth-first search and depth-first search.Generally,the number of feasible association sequence would be an enumerable number since the QoS of the air-to-ground communication link would be the key factor of UAV’s trajectory optimization.Moreover,it is proposed to refine the trajectory planning range if the GBSs are at the opposite direction for flight path planning.Then,the comparison among the candidate association sequence would be affordable.Based on the a feasible GBSUAV association sequenceB=[B1,...,BN],the time duration of the UAV flight can be divided intoNsegments aswhereTndenotes the time duration when the cellular UAV is served by GBSBn.Apparently,the optimal UAV trajectory during the timeTnwould be straight flight with the maximum velocity from the handover pointun−1of entering the GBS cell to the handover pointunof leaving the GBS cell[36].Therefore,the original objective function of minimizing the total flight time of UAV can be equivalent to that of minimizing the total UAV flying distance.Then,the optimization problem can be reformulated asP2,which is aiming to jointly optimize the UAVGBS association sequenceBand the handover points location{un}Nn=0. The above optimization problem can be divided into three subproblems:(1) GBS-UAV association sequence selection and(2)the shortest flight path design with the given GBS-UAV association sequenceBk.In the next section,we propose an efficient algorithm to obtain the minimized flight trajectory with the given GBS-UAV association sequenceBk.Then,the optimal trajectory of problemP2 can be obtained by comparing the optimal trajectories of the candidate GBSUAV associated sequencesBk.(3) we revealed the tradeoff between mission completion time and flight energy consumption of UAV. In this subsection,we assume that the UAV-GBS association sequence is predefined.Therefore,we omit the UAV-GBS association sequence indexkfor the sake of brevity so it is stated asBin this subsection.Without loss of generality,the feasible handover regionRnbetween two GBSs in the given GBS-UAV association sequenceBcan be presented as: It is noted that the optimal GBS-UAV association sequence should maintain the non-repeated GBS property and the handover location between two GBSs should be located on the intersection coverage boundary from [36].Then,the possible handover location region can be expressed as: where WhereBnadenotes the handover event occurs at the boundary ofgBnGBS,andBnbdenotes the handover event occurs at the boundary ofgBn+1.In a given UAV-GBS association sequenceB,the region of the UAV handover point can be determined by the formula Eq.(21),Eq.(22),anduncan be effectively obtained by searching the region.Therefore,the problemP2 can be solved by finding all the handover points{un∗(B)}Nn=0under the given sequenceBi.Therefore,problemP2 reduces to the following GBS-UAV association optimization problem.The flight trajectory optimization problem of minimizing the total flying distanceP3−Bcan be formulated as: Whereu0=uI,uN=uF.This optimization problem is difficult to solve by classic optimization techniques.In [36],graph theory and convex optimization are adopted to obtain the suboptimal solution.However,there is performance gap with optimal solution due to the GBS-UAV association sequence selection being not optimal and quantization levels not sufficiently large.Moreover,the complexity of the solution in[1]is dramatically increased if the performance gap from the optimal solution should be small enough.Based on the given feasible GBS-UAV association sequenceB,the initial feasible trajectory can be obtained by sequentially connecting all the centers of the GBS circles with initial/final location as shown in Figure2.The handover points between two adjacent GBS circles can be stated as: It is noted that there are two handover points that can be selected for the UAV,which can provide an opportunity to optimize the trajectory design.In the following,we propose an iterative path searching algorithm based on geometric inequality.Applying the triangle inequality [38],the length of the UAV’s trajectory can be shortened by sequentially connecting the handover points and initial/final location as shown in Figure2.As the handover operation can be occur either at theBnaboundary or at theBnbboundary,the handover points can be iteratively updated by alternatively selecting the handover boundary.Without loss of generality,we select the boundaryBnaas the handover boundary for the initialization.Then,the handover points can be presented as[ˆu1a,0,ˆu2a,0,...,ˆuN−1a,0]. Figure2.Illustration of initial handover point selection. Figure3.Illustration of handover point selection in the first iteration. Then,the triangle inequality can be presented as: Moreover,we propose to alternately choose the boundaryBnbas the handover plane to update the handover locations.Then,the handover location of the first iteration can be updated as the intersection betweenandBnbas shown in Figure3,which can be presented as: Furthermore,the trajectory can be updated by connecting the handover pointswith initial/final locations.The UAV’s trajectory can be updated as: Figure4.Illustration of handover point selection in the second iteration. The following geometric inequality of UAV flight distance holds true to demonstrate that it can shorten the flight distance. It is noted that the first handover pointbelongs to the boundary ofB1b,which means the updated UAV trajectoryT2served by the first GBS would have the same trajectory withT1.It can be drawn as the violet line in Figure3.In the second iteration as shown in Figure4,using the same approach to deal with the boundaryBna,the handover pointscan be obtained as follows: The updated UAV trajectory at the second iteration can be written as: Figure5.Illustration of handover point selection in the third and last iteration. The UAV flight distance can be further shortened based on the following geometric inequality: It is noted that the last handover pointbelongs to the boundary ofwhich means the updated UAV trajectoryT3served by the last GBS would have the same trajectory withT2.This is depicted as the green line in Figure4. Until now,we can conclude that the handover points can be alternately updated as follows: Figure6.Illustration of non-turning handover point. And the UAV flight distance can be presented as: Proposition 1.There are two types of handover points in the optimal trajectory design:one is non-turning handover point,the other is turning handover point.For any non-turning handover pointorit should be aligned in a straight line with its adjacenthandover pointsorForany turning handover pointorit must be lo-cated at the intersection between Bna and Bnb. Proof.This can be proved by proof of absurdity.Without loss of generality,we consider the scenario of the optimal handover points located at the boundaryBna.Assume the optimal handover pointsare obtained.Consider a specific optimal handover pointthat is not the intersection betweenBnaandBnb,and is not aligned with its adjacent handover points (and) in a straight line.It can be drawn as shown in the Figure6. For this scenario,we propose a method to find a new handover points which can shorten the flight distance as follows: 1.Select an arbitrary pointfrom vectorwithin the regionRn. 2.It can be easily proved that the following triangle inequality is true. 3.The new handover point can be obtained as: Therefore,there have other candidate handover points to minimize the flight distance and the handover pointsare not the optimal solution for the UAV trajectory design.In other words,it is proved our proposition:if the handover point is not located at the intersection betweenBnaandBnb,then,the optimal handover point should be aligned with its adjacent handover points in a straight line. Based on the proposition 1,the proposed UAV’s trajectory design can be efficiently converged via determining the types of handover points and checking the relationship with the adjacent handover points.It is noted that the alternative iteration method can guarantee that the UAV’s trajectories within each association GBS circle are updated towards the optimal trajectory simultaneously.The main complexity of the proposed solution is dominated by implementing the feasible UAV-GBS association sequence using the Dijkstra algorithm,which has low complexityO(L2). In this subsection,the UAV trajectory planning with connectivity constraint can be efficiently solved by an triangular inequality alternate iteration algorithm based on a unified graph theory and geometric inequality design framework as follows: 1.Apply graph theory to check the feasibility of the UAV trajectory with connectivity constraint and list the candidate feasible UAV-GBS association sequences for finding the shortest path. 2.For each given feasible UAV-GBS association sequence,we adopt the alternately iteration method with geometric inequality to design the shortest flight path.Through analyzing the properties of two types of handover points,the convergence of the proposed algorithm can be easily verified. 3.Comparing the length of the shortest UAV flight paths with different UAV-GBS association sequences,the optimal solution of Problem P1 can be obtained. The above algorithm is summarized as Algorithm 1. ? The cellular-connected UAVs gains the shortest distance when the direction of the UAV does not change,the handover points of UAVs between the GBSs will be in a straight line.However,it is necessary to change the flight direction sometimes to meet the limitation of real-time connection.When the flight direction of UAV changes,the turning handover point of the UAV’s flight is the switching point between the GBSs,which only appears at the edge of the overlapping area of GBSs coverage to determine the shortest path. This subsection focuses on the characterization of the optimal Time-Energy (T-E) tradeoff under any givenIn this paper,we assume that the UAV is flying at a constant speed.It is worth noting that the propulsion energy depends on the UAV flying velocity as well as its acceleration.Due to the flight trajectory is composed of several straight lines,moreover,the QoS of UAV is satisfied by the connectivity range.The propulsion energy for UAV’s acceleration can be ignored for this scenario [31].Then,for ease of explanation and calculation,the velocity of UAV can be modeled by constant value to evaluate the propulsion energy of UAV.The propulsion power consumption of rotary-wing UAV [31]flying with speedVcan be modeled as: WhereP0andPirepresenting the blade profile power and induced power in hovering status,which are two constants.Utipis the tip speed of the rotor,blade,v0denoted the mean rotor induced velocity in hover,d0andsare the fuselage drag ratio and rotor solidity,ρandAare the air density and rotor disc area.With given UAV trajectoryu(t),the propulsion energy consumption can be expressed as: Where min‖u(t)−gBi‖ ≤Rdenoted the UAV flies from the initial position to the final position always under the coverage of the cellular network.The Pareto boundary ofCwhich is defined as the set of all pairs(T,E)at which it is impossible to decrease one of them without increasing the other.To characterize the Pareto boundary,one solution is to obtain the minimum completion time for any given value of energy consumption while completing the mission.Then,it is important to study minimum completion time and minimum energy consumption i.e.,the lower-bound ofTandE.The time minimization(TMin)problem can be formulated as Solving (P4-TMin) can obtain the minimum time point of the Pareto boundary.Denote the lower-bound of mission completion time asTmin,the corresponding energy is denoted asETmin.The energy minimization(EMin)problem can be formulated as LetEmindenote the optimal objective value that is obtained through solving(P4-EMin);the corresponding time is denoted asTEmin.Solving (P4-EMin)and (P4-TMin) can determine two extreme points of the Pareto boundary of the T-E region that indicate minimum mission completion time and the minimum energy consumption,which are represented as(Tmin,ETmin)and(TEmin,Emin) With given optimized path length in Eq.(22)and the constraints in Eq.(35),Eq.(36),Eq.(37),Eq.(38),the problem of P4 can be effective solved. In this section,we provide numerical results to validate the performance of our proposed trajectory design.We have taken some of parameters values from[1].The fixed altitude of the UAV and each GBS is set asH=90mandHg=12.5m,the maximum speed of UAVs is assumed to bevmax=70m/s.The channel power gain at the reference distanced0=1mis set asρ0=80dB.According to the given parameters,the maximum communication distancedmaxbetween UAV and GBS can be set to 500m. Table1.Simulation map settings. Figure7.The topology of different UAV-GBS sequence. Figure8.The trajectory of different UAV-GBS sequence. The association sequences between the UAVs and the GBSs is one of the key factors determining the length of the flight path.We evaluate the performances between our proposed solution and the method I in[36].In Figure7,the UAV has two candidate association UAV-GBS sequences topology for it flying from initial location to the final location based on Figure1.Based on the Method I proposed in literature[36],the GBS association sequence I would be selected to optimise the flight path.Furthermore,the optimal flight path can be obtained as the red path based on the iterative algorithm in Figure8.However,the red path is not the shortest flight path for this scenario.Adopting our proposed iterative optimization algorithm that we list all possible GBS association sequence paths and compare their length to obtain the final optimal result.The blue path can be obtained according to the GBS association sequence II that is the shortest flight path.Therefore,Figure8 proves that our proposed algorithm can guarantee the optimal flight path can be selected,which is outperform than the Method I in[36]. Figure9.The trajectory of proposed solution and Method II with different Q. Table2.UAV simulation parameters. Next,we investigate the performances of our proposed solution and Method II in [36].As shown in Figure9,there are multiple paths involving two algorithms that the UAV flying from initial location to the final location.The shortest one (blue path) is based on our proposed iterative optimization algorithm.The other paths are based on Method II in literature [36]with different quantization stepQ.It can be observed that the flight path of the UAVs according to differentQvalues would be fluctuated.The flight length comparison can be drawn as shown in Figure10.As the value ofQincreases,the length of the flight path obtained by Method II is gradually approaching the length obtained by our proposed iterative optimization algorithm.The algorithm complexity of Method II isO(L4Q2).whereLis the number of all GBSs.The algorithm complexity of Method II increases as theQvalue increases.The algorithm complexity of our proposed iterative algorithm iswhereO(L2) is the complexity of Dijkstra algorithm which is used to search the candidate UAV-GBS association sequences.Srepresents the number of association sequences whose path lengths need to be compared.Iidenote the number of iterations ini −thcandidate UAV-GBS association sequence.Nidenote the number of GBSs ini −thcandidate UAV-GBS association sequence.Figure11 shows the relationship between the number of GBSs in the UAV-GBS association sequences and the number of algorithm iterations to obtain the optimal solution.As the number of GBSs increases,the number of iterations gradually increases.The figure shows that the change in the number of iterations is relatively small for different numbers of GBSs.The algorithm complexity of our proposed iterative algorithm is much lower than Method II.Next,we comprehensively evaluate three different algorithms.TheQvalue of Method II mentioned in the literature [36]is set to 8.In the Figure12,we can see that the proposed iterative optimization algorithm is closer to the optimal solution than other algorithms.Table3 shows the flight time of different algorithms at the same speed V=30m/s.The completion time of Method I is obviously higher than that of Method II and the optimization algorithm.The completion time of method II gradually decreases as theQvalue increases.When the completion time of method II and optimization algorithm is similar,the complexity is higher. Figure10.The flight length of proposed solution and Method II with different Q. Figure11.Number of iterations with different number of GBSs. Figure12.Illustration of different trajectory designs. Finally,Figure13 shows the complete Pareto boundary of the T-E region,the T-E region is located above and to the right of the Pareto boundary.In order to facilitate the calculation,we take the flying speed of the UAV to an integer.The flying speed of the UAV with the lowest power isV=13m/s,the flying speed of the UAV with the least energy consumption isV=17m/s.We can observe the minimum flying time of the UAV decreases as the energy increases.We can make a trade-off between UAV flight mission time and flight energy consumption. Figure13.minimum flight time versus energy consumption for UAV. Table3.Completion time of different algorithms. In this paper,we investigate the trajectory optimization problem of the UAVs in the case of cellular network connections.We converted the shortest path of the UAVs from initial location to the final location at a constant speed and altitude.We reformulate the problem and proposed efficient algorithm by combining of graph theory and geometry inequality scheme.As the number of iterations increases,the results tend to approximate the optimal solution.We studied the timeenergy tradeoff for UAV.The simulation results prove the feasibility of the algorithm. The UAV adopts the cellular network to connect with the GBSs in real time.The cellular network has strong anti-interference ability,and the channel interference between multiple UAVs is also small.There are 3D beamforming,antenna beam selection,collation,power control,and inter-cell interference coordination,etc,which can be applied to reduce aerial interference.The triangular inequality iterative algorithm is mainly applied to the shortest path problem of a single UAV flying from the starting point to the end point under the constraints of cellular connection.In reality,the triangular inequality alternate iteration algorithm can also be applied to some multiple UAVs scenarios.In the scenario where the flying height of the UAV is different,multiple UAVs fly from different starting points to the ending flight paths without overlapping.The inequality iteration algorithm can be used to obtain the shortest path.In the scenario where multiple UAVs have the same flight altitude,if the flight areas of the UAV can be separated,and this algorithm can still be used to achieve the shortest flight path while ensuring safety.We will explore how to properly distribute the mission to separate the flight areas of UAVs in future work. This paper considers the UAV trajectory design under the real-time connectivity constraint of the GBSUAV,the premise of triangular inequality alternate iteration algorithm is that the coverage areas of GBSs overlap each other.However,the quality of connectivity constraint of the GBS-UAV communication link may not apply for other disconnection scenarios.How to extend our results to connectivity outage is an interesting direction worthy of further. ACKNOWLEDGEMENT This work was supported by National Natural Science Foundation of China (NO.61703197 and NO.62061027).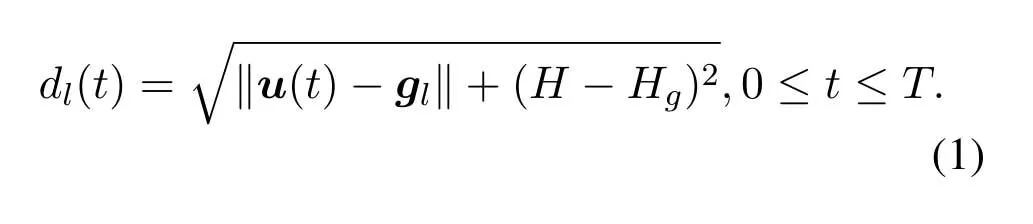
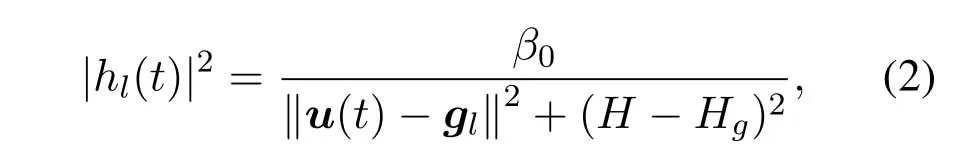
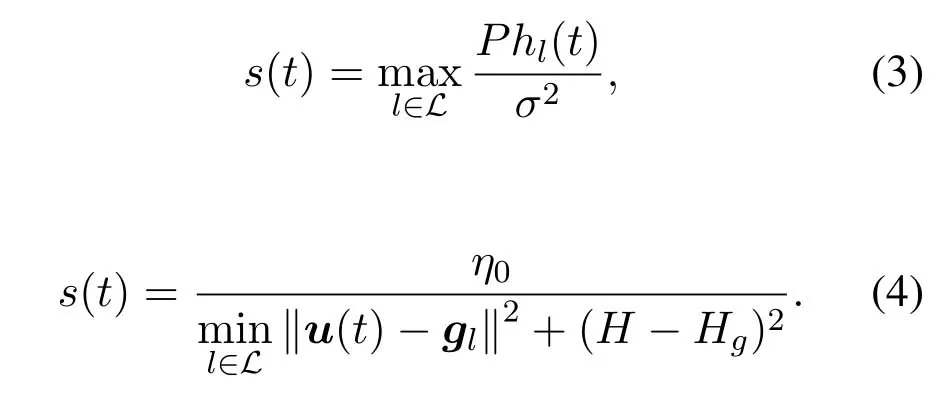
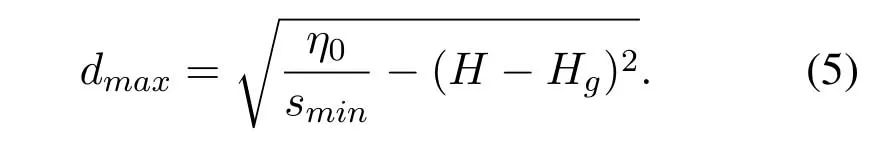
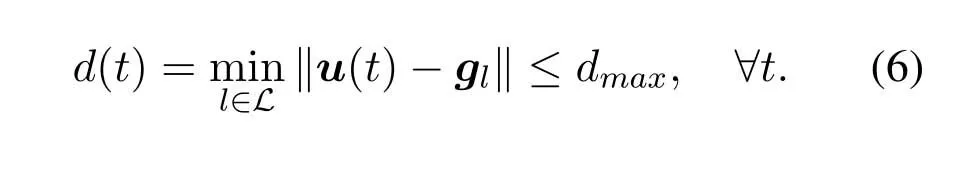
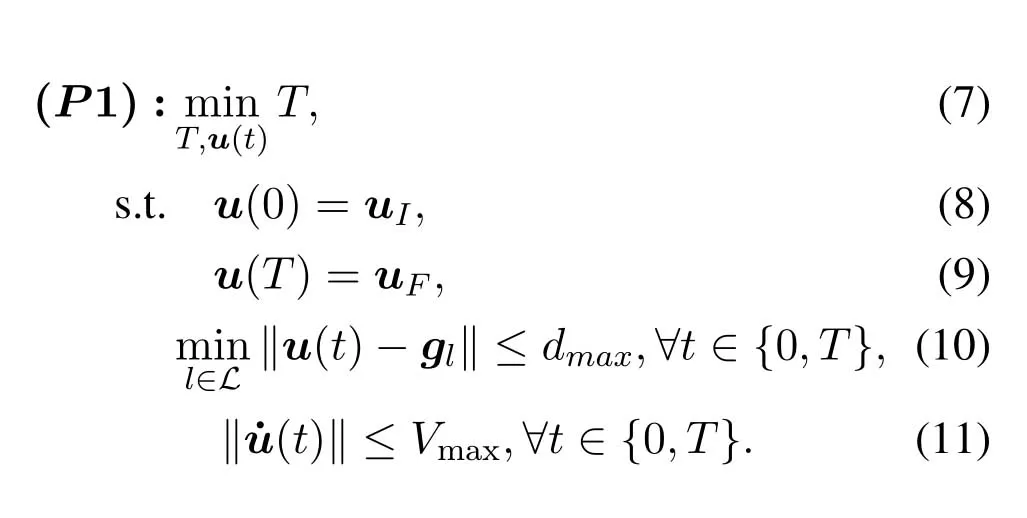
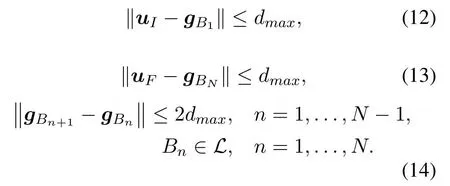
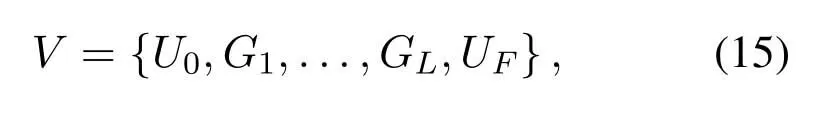
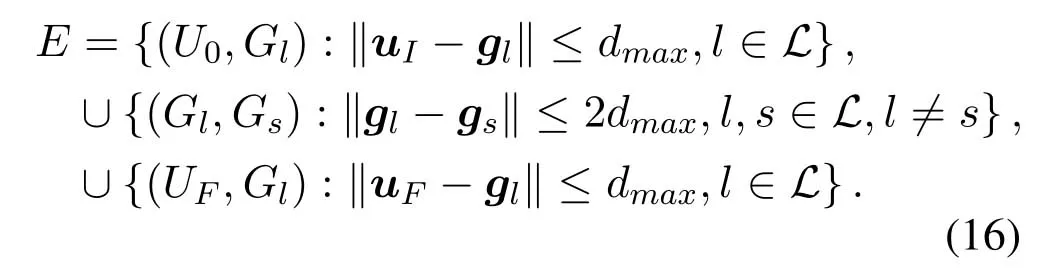
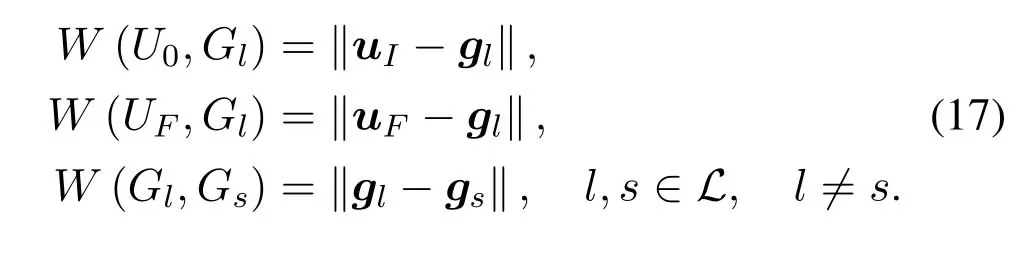
III.PROPOSED SOLUTION
3.1 Efficient Algorithm for Handover Location Design Based on Geometric Inequality
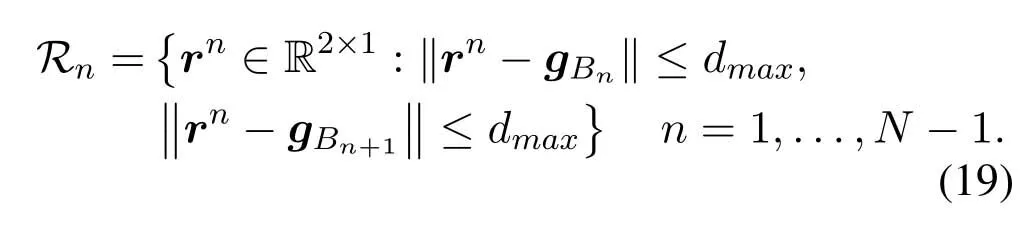
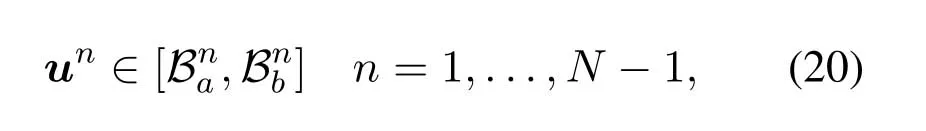
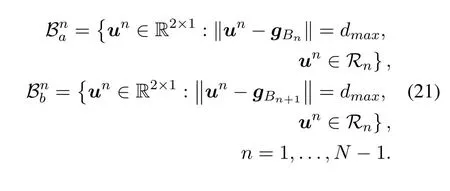
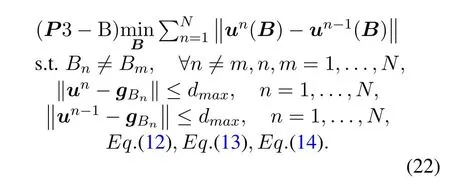
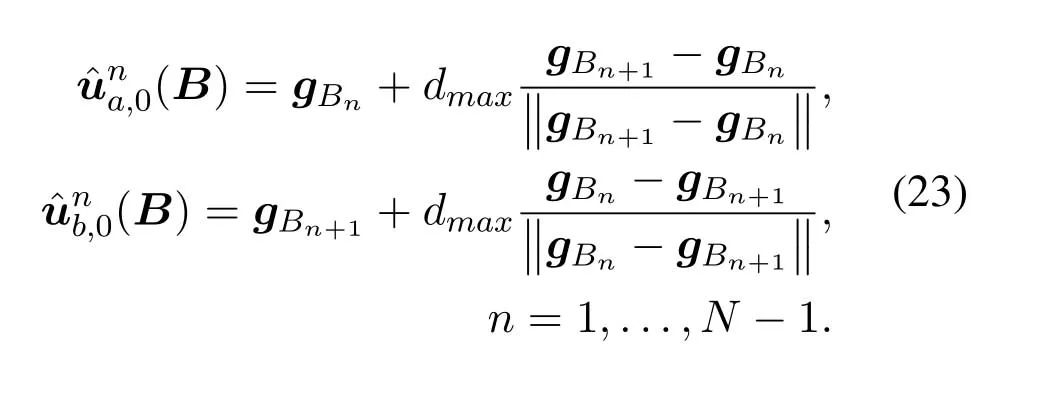

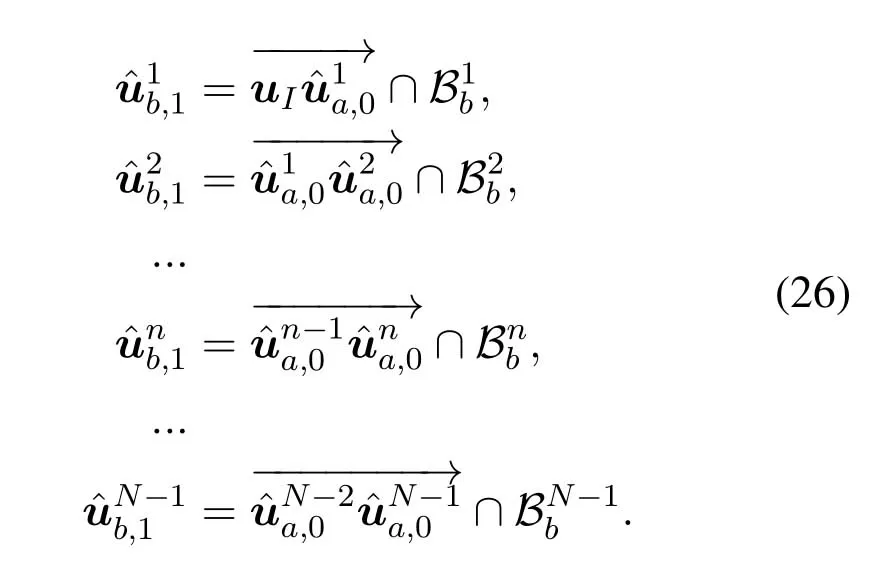
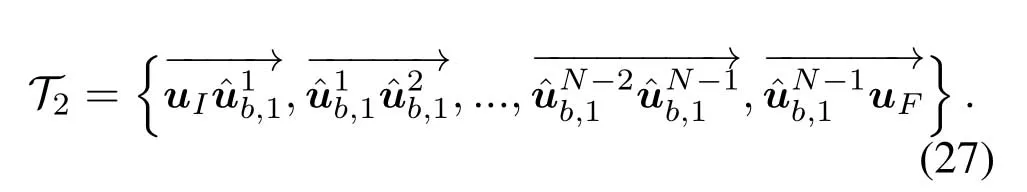
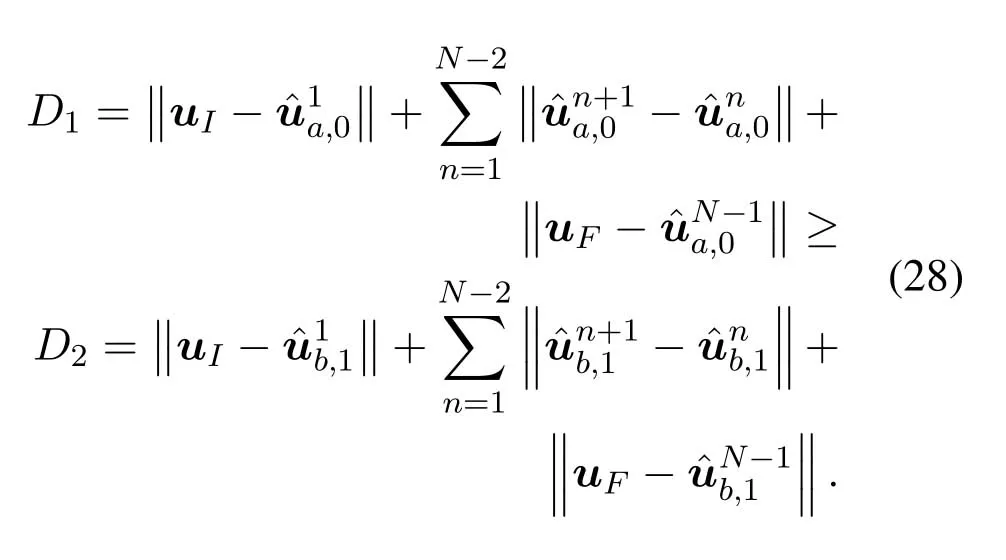
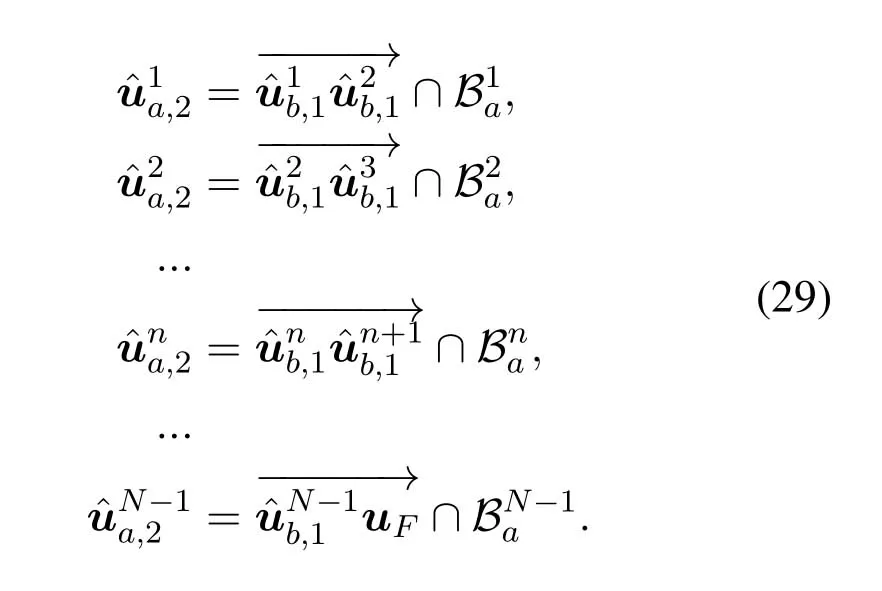
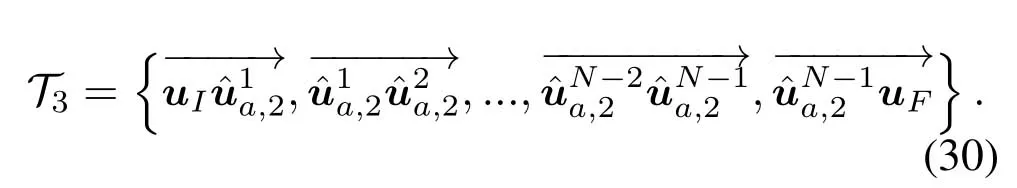
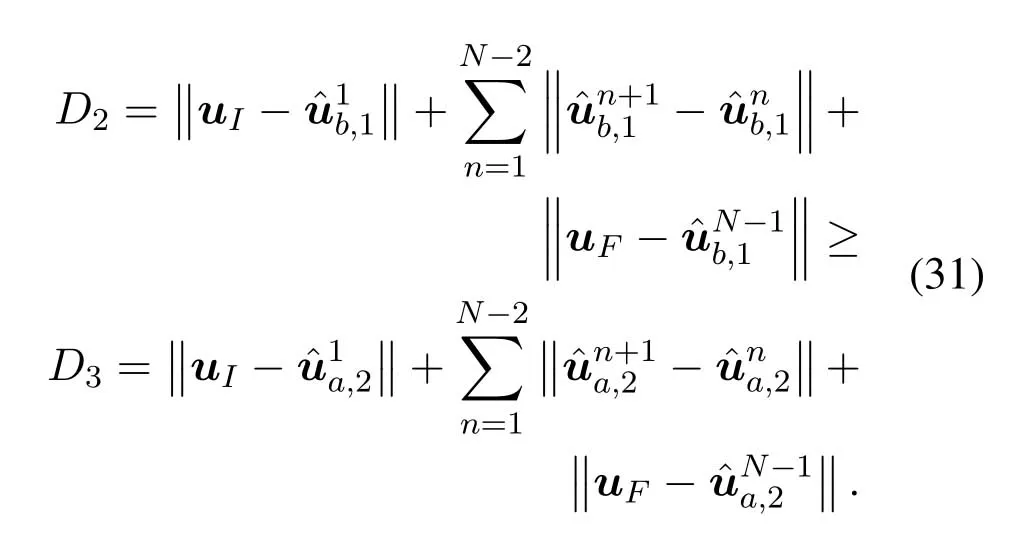
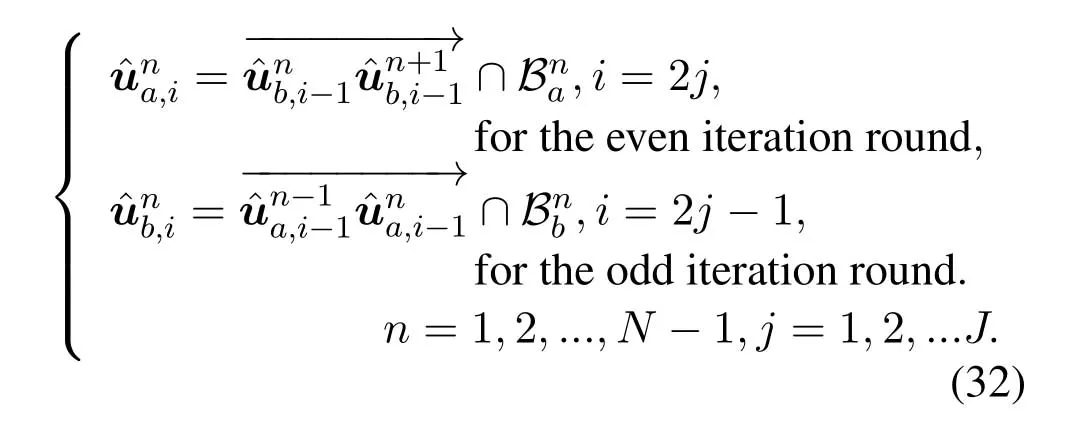
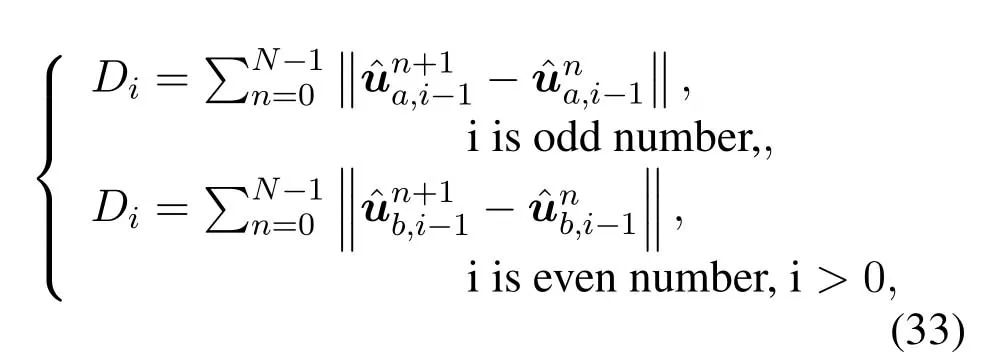
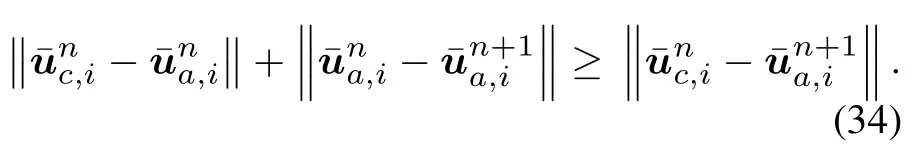
3.2 Summary of Geometric Inequality Based Algorithm for Problem P1

3.3 The Tradeoff Between Completion Time and Flight Energy Consumption
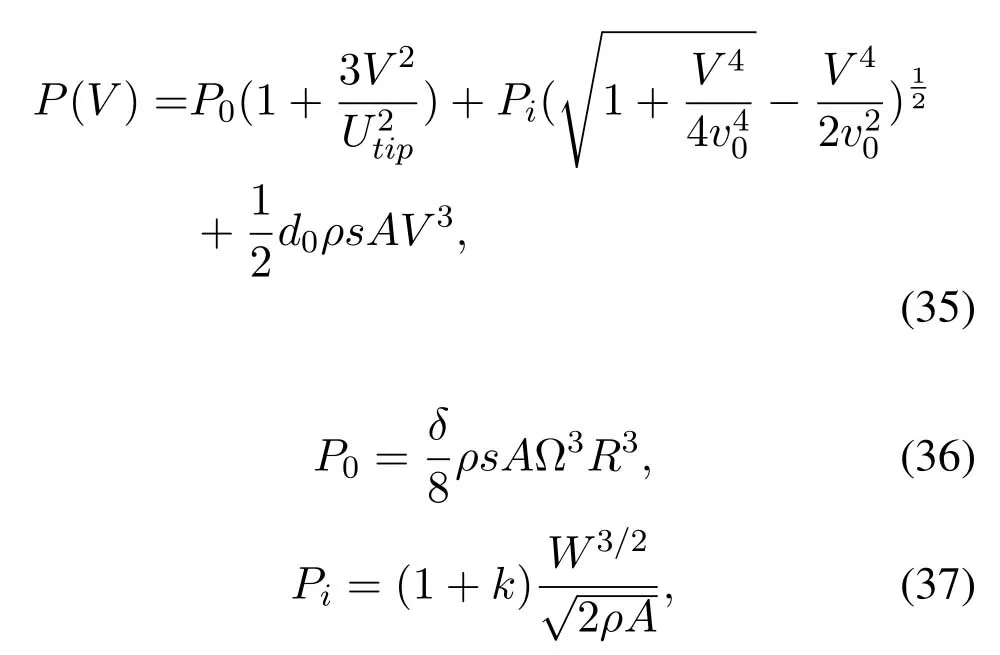
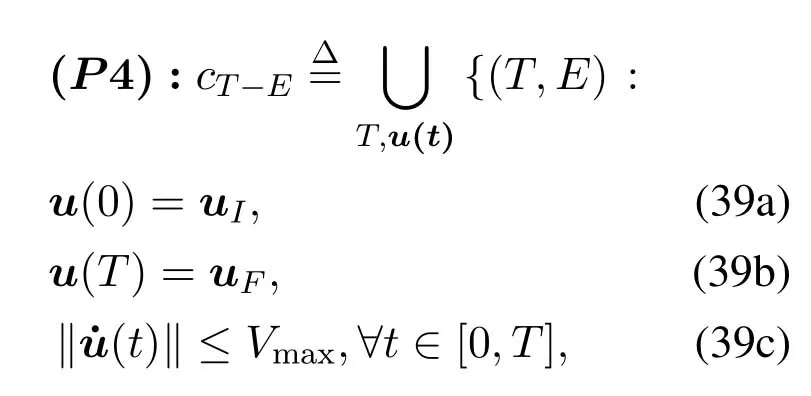
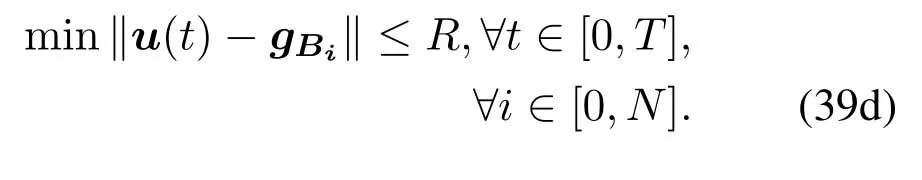
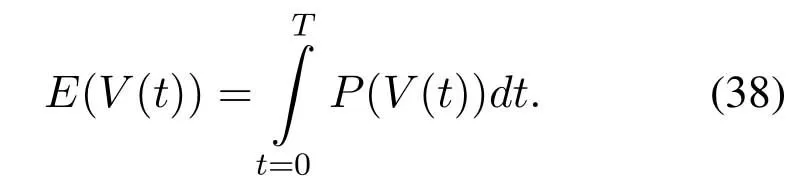
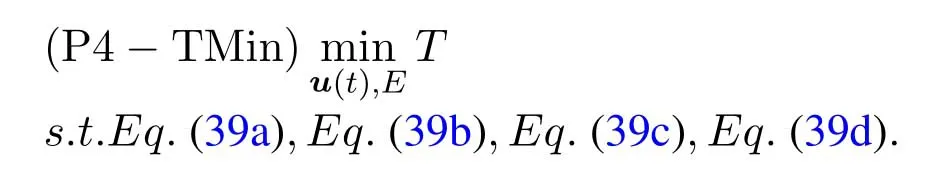
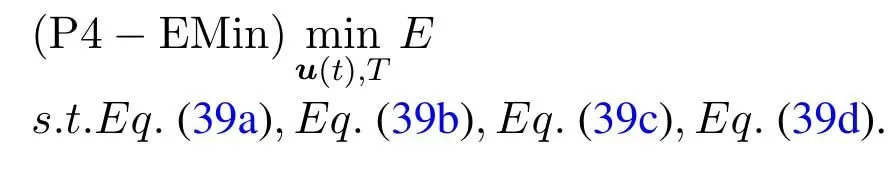
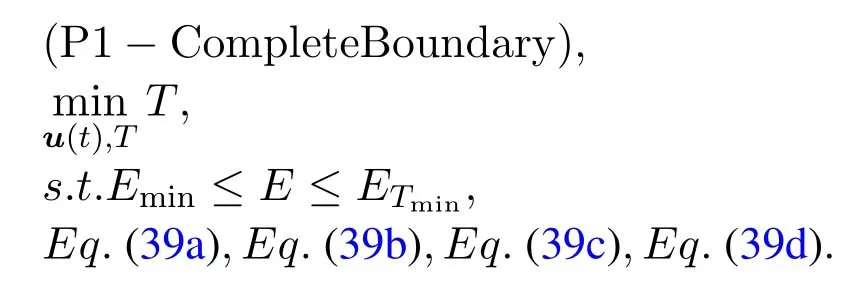
IV.SIMULATION RESULTS

V.CONCLUSION
- China Communications的其它文章
- Future 5G-Oriented System for Urban Rail Transit:Opportunities and Challenges
- Multi-Stage Hierarchical Channel Allocation in UAV-Assisted D2D Networks:A Stackelberg Game Approach
- Performance Analysis of Uplink Massive Spatial Modulation MIMO Systems in Transmit-Correlated Rayleigh Channels
- Development of Hybrid ARQ Protocol for the Quantum Communication System on Stabilizer Codes
- Coded Modulation Faster-than-Nyquist Transmission with Precoder and Channel Shortening Optimization
- Analysis and Design of Scheduling Schemes for Wireless Networks with Unsaturated Traffic

