基于车辆成组的V2V协同计算卸载策略研究

0 引言

随着无线通信技术和车载互联网的爆炸性发展，越来越多的车辆配备了具有通信、存储、计算和人机交互能力的车载单元［1］。许多智能交通应用程序可以在车载单元上运行，同时也有相当比例的车载应用对计算资源与能源需求极大，被称为计算密集型应用。面对这些应用，单个车载单元的计算能力可能无法完全满足要求。车联网边缘计算（VEC）的出现为解决这一问题提供了新的途径［2］。VEC 与移动边缘计算（MEC）相比，其终端从个人移动设备变为了高速移动的车辆。通过将核心网的计算资源部署到车辆网络的边缘，路侧单元（RSU）覆盖范围内的车辆可以将部分或全部任务卸载给部署在RSU 的MEC 服务器以获得更好的计算服务，这种方式称为车辆到基础设施（V2I）卸载［3］。另一种方法是将任务卸载给其他有计算能力的车辆，称为车辆到车辆（V2V）卸载［4］。与V2I卸载相比，V2V 卸载可以充分利用其他车辆的计算资源，缓解路边MEC服务器的压力。

通过V2I 卸载，车辆可以将计算任务卸载到部署在RSU的MEC服务器来完成计算。然而，在典型的车载网络场景中，车辆在计算卸载过程中高速移动，使得V2I 卸载面临许多问题，如车辆可能在计算结果返回之前离开RSU 覆盖的小区，高速移动会影响无线链路质量。在热点地区，由于交通拥挤和移动终端数量过多，RSU 会承受很大的负载［5］。因此，如何充分利用闲置车辆的大量计算资源来降低RSU 的负载是计算卸载的关键问题之一［6］。文献［7］考虑将卸载到负载过重RSU 的计算任务转移到周围负载较轻的RSU，并通过车辆将计算结果带回轻负载RSU 的范围内。在文献［8］中，V2I卸载问题被视为车辆与RSU 之间的匹配问题，通过求解任务车辆与RSU 之间的最优匹配来最小化所有车辆的平均计算时延。在文献［9］中，计算任务被分成若干个无依赖关系的子任务，分别卸载到沿途经过的各个RSU，通过车速、链路质量、RSU 覆盖半径、子任务大小等因素预测经过每个RSU 覆盖小区的时间，以此来分配子任务数量，确保计算结果的返回。

对于车载网络中的V2V 卸载，车辆通常成组来共享信息并互相帮助完成计算任务。文献［10］提出了一种协同车辆边缘计算网络架构，该网络中的多个相邻车辆组成一个组，组中的车辆可以通过无线链路相互通信和协作完成计算任务。文献［11］考虑了车组内成员的协作以及计算任务的可分割性，其中组内的不同车辆具有不同类型的计算任务。文献［12］将计算任务分为顺序子任务和依赖子任务，并提出了一种任务调度算法确定任务的最优计算顺序。在文献［13］中，作者将计算任务划分为若干有先后顺序的子任务，并将任务分配问题看作并行处理器的最小完成时间问题，提出了一种基于列表调度的任务分配算法，以最小化任务的总完成时延。

然而，上述研究并没有充分考虑计算卸载过程中车组内的车辆之间保持稳定连接的时间以及车辆在计算过程中离开车组的情况。本文联合考虑车组成员能保持稳定连接的时间和车辆突发离组的情况，具体分析了车辆因故障离组和中途主动离组的2 种情形。对计算任务根据不同类型划分子任务，设计了一个动态的组内计算任务分配算法，其中计算任务卸载总时延包括任务上传时延、任务计算时延和结果返回时延。为了使整个车组计算任务的总时延最小，提出了一种车组内计算任务分配算法。该算法调整了子任务的分配方式，通过迭代实现总时延最小。

1 系统模型

1.1 网络拓扑

本文研究单向直行道路上，车组在行驶过程中的计算卸载问题，场景如图1所示。在该场景中，路侧单元RSU 均匀分布在道路两侧，其覆盖范围互不重叠。这n个RSU 记作R={R1,R2...Ri...Rn}，其中Ri表示第i个RSU。每个RSU 的覆盖半径为r，相邻RSU 之间由光纤连接。同车道内前后M辆车组成一个车组。用U=(U0,U1...Ui...UM-1)表示车组内的车辆，其中U0的计算任务仅靠自己不能完成，称为任务车；组内其他车辆或多或少有可以提供给任务车的空闲计算资源，称为服务车。本章中任务车U0的计算任务分为4 种类型，分别是图像处理、视频处理、交互式游戏、增强现实［14-16］，可以用L=(LA,LB,LC,LD)表示，每种类型的任务可以划分成若干相等大小的不相关的子任务，以I作为子任务划分的大小单元。

整个车组以共同的速度v向前行进，车组内每一辆车的计算能力分别为f=(f0,f1,...,fm-1)，单位是CPU圈数/s，其中f0是本地计算的计算能力。

1.2 通信模型

在车辆形成车组后，由任务车U0作为车头来协调组内车辆和分配计算任务。组内车辆分享行驶路线使得U0可以获取组内各车辆能与车组保持稳定卸载的时间信息，用τ={τ1,τ2...τm-1}分别表示组内车辆预计离开车组的时间节点。要尽量保证分配给车辆Ui的计算任务在τi时间内完成并返回。组内车辆通过LTE-V 方式进行通信，根据香农公式可知任务上传到组内服务车的速率如式（1）所示。

式中：

B0——分配给任务车的信道带宽

h——上行信道衰落系数

N0——高斯白噪声功率

pi——卸载到第i辆车的子任务数量

图1 基于车辆成组的V2V卸载

任务车将带宽分成M-1 份向组内每一辆服务车传送分配的任务。卸载到第i辆车的任务传输时间如式（2）所示。

然后考虑计算结果的返回。由于返回的计算结果数据量通常很小，所以车组内的计算结果返回时延可以忽略不计。相邻RSU 之间的光纤带宽为B，子任务返回结果的数据量为dbit。任务返回时由于返回数据量很小，在RSU 之间的传输时间可以忽略不计，所以任务的返回时间主要由每次经过RSU的等待时间tw决定。子任务结果在RSU 之间返回时每经过一个RSU 都要有一个等待时延，经过n个RSU 则返回时延为ntw。

1.3 计算模型

本文假设车组内任务车辆的计算负载较重，且计算任务可以分割为若干相等大小的无依赖关系的子任务。执行计算任务需要耗费车辆的计算资源，通常使用执行该计算任务所要耗费的CPU 圈数来表示。任务执行时的复杂度用执行单位大小的任务需要耗费的CPU圈数来表示。假设4种不同类型任务的计算复杂度不同，分别是αA,αB,αC,αD，单位为CPU 圈数/bit。

考虑到任务分割，这4 类任务划分为若干个子任务。4 种任务的每个子任务数量表示为NA,NB,NC,ND，子任务总数为N。

假设每个子任务的大小为Ibit。车组中的每辆车都由任务车辆分配了一定数量的子任务，分配给第i辆车的4 种任务的子任务数分别为pi={piA,piB,piC,piD}，则第i辆车的计算时延包括了4 种任务的计算时延，可通过式（3）计算。

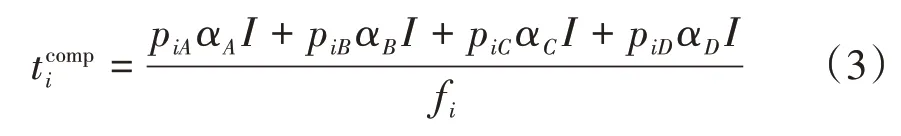
如上所述，组内的每辆车都被分配了这4 类任务中若干数量的子任务。本文通过调整每辆车被分配的子任务数量以降低总任务时延。

2 算法设计与实现

2.1 问题建立

对于组内被分配了计算任务的服务车辆，在任务计算完成后将计算结果直接返回给任务车辆。对于中途离开的服务车辆，考虑该车辆在离开车组后继续进行计算工作，在计算完成后借助RSU 将计算任务返回给原车组中的任务车辆。

车辆离开车组的原因包括客观因素与主观因素。例如车辆在行驶过程中突发故障就属于客观因素。对于这种情况，可以根据已行驶时间估计车辆在未来一段时间内出故障的概率。对于第i辆车在任务过程中发生故障的概率可以用式（4）表示。

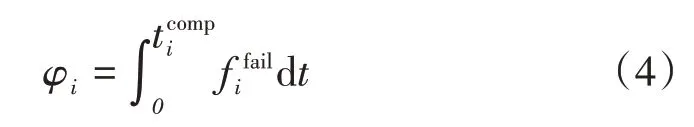
式中：

车辆也可能因驾驶者的主观意愿临时变更行驶方向或是需要在原地停留一段时间。对于这种情况，可以根据车辆历史参与计算任务卸载的情况来推测本次任务过程中会发生主观离组的可能性。假设车辆i历史参与任务卸载的次数为yi，在任务过程中主动离开的次数为xi，通过车辆历史参与任务卸载次数和中途离开的次数的比值可以推测其本次任务过程中离组的概率，具体如式（5）所示。

根据上面的2个因素，如果有一个因素发生，车辆就会离开车组。因此，第i辆车在任务过程中离开车组的概率可以用式（6）算出。

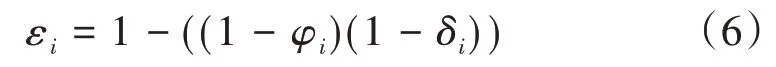
车组中所有车辆离开车组的概率，用ε ={ε1,ε2,...,εm-1}表示。假设车辆在离开车组后保持原地等待，同时不停止任务的计算过程，同时车组继续保持前进。表示第i辆车离开车组的时刻。离开车组的车辆在完成计算任务后将计算结果返回给当前所在的RSU。车组在车辆i离开车组后经过的RSU 数量由式（7）给出。

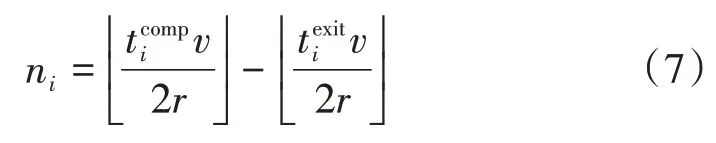
离开车组的服务车辆可以通过式（7）获得车组当前所在的位置，并将结果返回到其范围内的RSU。接下来，结果将在相邻的RSU 之间传输，并最终到达车组当前所在的RSU。返回时延是由式（8）定义。

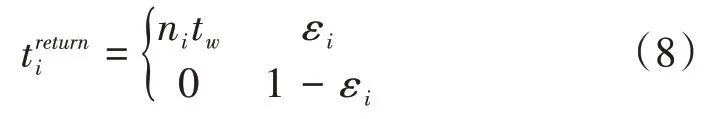
车组中每个车辆的总任务时延如式（9）所示，是任务上传时延、任务计算时延和任务返回时延之和。

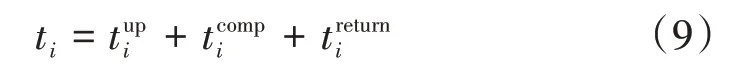
整个车组的总任务时延定义为车组中所有任务完成的时间，也就是组内最后一个车辆完成任务的时间。本文目标是通过优化组内车辆子任务的分配，以最小化任务完成的总时延。

因此，本文所讨论的时延最小化问题可以表述为式（10）。

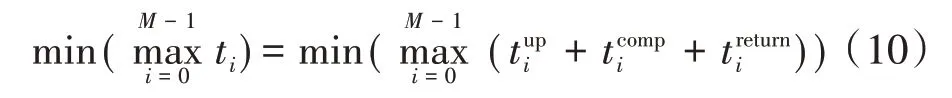
限制条件如下：

a）ti<τi

b）pi=piA+piB+piC+piD

d）0≤pi≤N

e）piA≤NA,piB≤NB,piC≤NC,piD≤ND

在上述条件中，条件a）是对每辆车中计算任务时延的限制，即每个车辆的计算任务必须在该任务的限制时延内完成。b）为子任务数量的约束条件，即分配给每个车辆的子任务数量等于4 种子任务数量的总和。c）以及d）是对每个车辆分配到子任务数量的限制，表明每辆车被分配到的每种类型的子任务数不超过车组内该种类子任务的总数。e）给出了车组内每种类型子任务数量上限的约束。

2.2 所提算法

通过分析发现，目标函数属于混合整数规划问题，存在最优解。这类问题在问题规模较小时可以通过暴力枚举法在较短时间内找到最优解。然而当问题规模扩大后，暴力枚举所需的时间则呈指数级增长。具体来看，式（10）相当于将N个任务放进M个容器内，一共有MN种可能性，时间复杂度为O(MN)，属于NP-hard 问题。通过启发式算法在较短的时间内找出一个次优解也是解决这类问题的一个途径。本文使用模拟退火算法对该式进行求解，以得到较低时间代价的次优解。

在车组形成后，组内的服务车辆将路由、计算资源、历史完成情况、故障概率等信息发送给任务车辆。任务车辆然后根据式（6）预测在计算任务过程中各个服务车辆的离开概率。首先任务车辆在分配每一个子任务前，通过式（2）、式（6）、式（8）、式（10）分别计算将此子任务卸载到每一个服务车辆的卸载时延，然后根据贪心算法依次将4种类型任务的子任务分给组内的服务车辆。贪心算法的策略是每个服务车辆被分配任务后累积自己的总任务时延，任务车辆将下一个子任务分配给当前总任务时延最小的服务车辆。在所有子任务分配完毕后，使用模拟退火算法优化子任务的分配方式，在所限定迭代次数内找出次优解。详细算法步骤如图2所示。

模拟退火算法的步骤包括以下几步。

a）随机在以下2个操作中二选一执行。

（a）随机选择车组内2辆车，交换其中一个不同类型的子任务。

（b）将车组内一辆车的一个子任务随机分配给另一辆车。

b）计算新的总时延与之前总时延的差值。

c）如果差值为负，即通过任务交换或任务分配得到的时延比之前低，则接受此操作。否则则按一定概率接受此次操作，接受概率与当前温度有关。

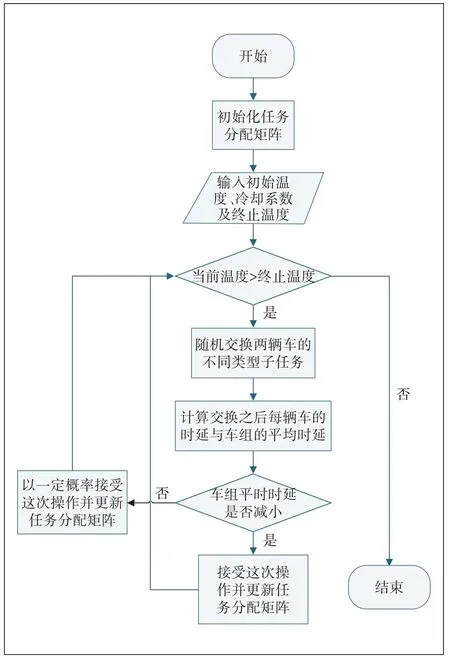
图2 车组内协同计算任务分配算法

d）将当前温度乘以冷却系数得到新的温度。

3 仿真与分析

本章通过仿真来验证所提算法的性能。仿真场景如表1所示。车组内车辆的计算能力为f={3×107，5×107，2×107，3×107，3×107}圈/s，4种计算任务的计算复杂程度分别是30、15、40、20［17］。具体参数设置如表1 所示。

所选取的对比算法分别是随机卸载算法以及贪婪卸载算法［18］。

a）随机卸载算法：4 种计算任务将随机数量的子任务分配给组内车辆。

b）贪婪卸载算法：贪婪分配算法在每次分配任务时都选择能使当前总计算时延最小的车辆进行分配。

图3 显示当车组内子任务总数为80 时，通过3 种算法分配任务的车组最小时延与迭代次数的关系。车组速度设定为18 m/s。结果表明3 种算法都能在一定次数的迭代内达到收敛。其中贪婪分配算法能较快获取极小值，在大约400 次迭代后将总时延降低到11.84 s。本文所提算法在约1 400 次迭代后收敛到最小值11.84 s。可以看出，当子任务总数量比较少时，这2种算法都能找到最小值。而随机分配算法时延大于其他2种算法，性能较差。

表1 仿真参数设置

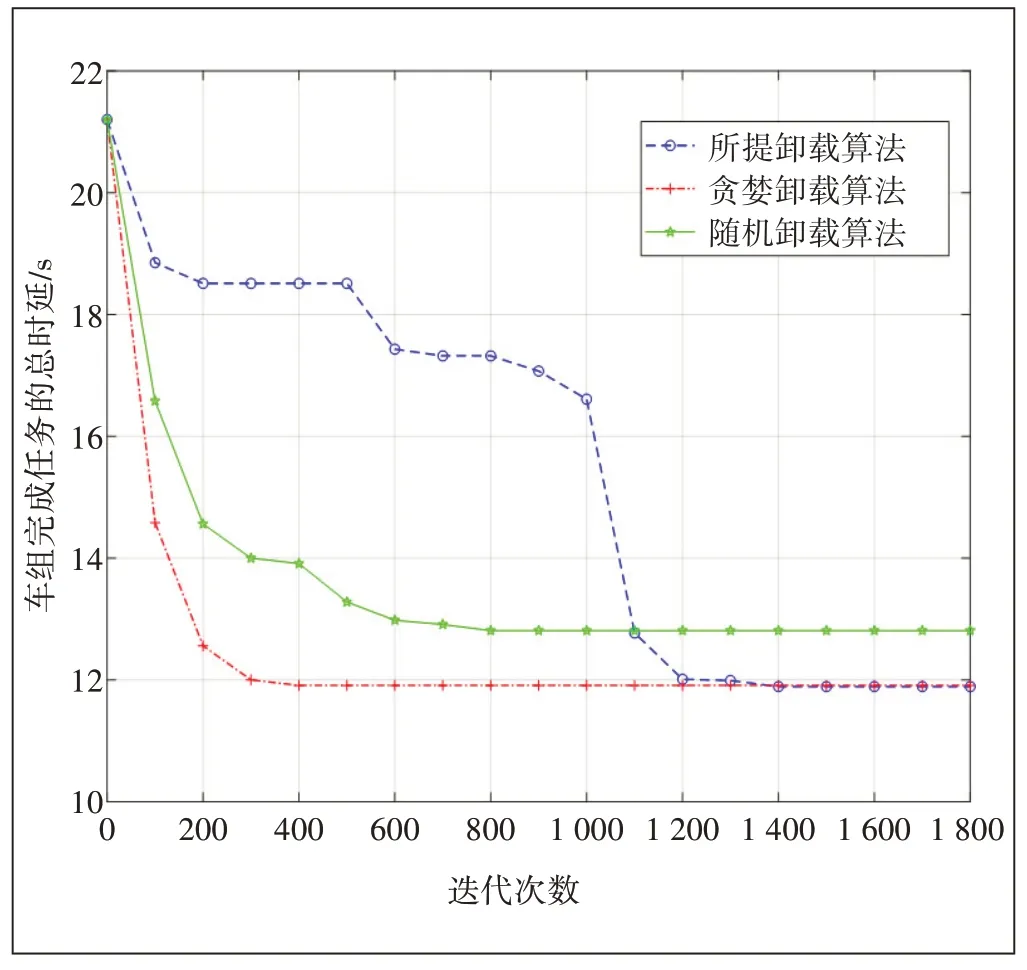
图3 N=80时车组总时延随迭代次数增加的变化

图4 展示的是当组内子任务数增加到135 时，通过3种算法分配任务的车组最小时延与迭代次数的关系，其中车速仍固定在18 m/s。随着任务数量的增加，可以看出，贪婪算法依旧可以较快地找到极小值，在约200次迭代后陷入局部极小值，由仿真结果来看，本文所提算法在约1 400 次迭代后找到了全局最小值17.64 s。随机任务分配算法性能较差。

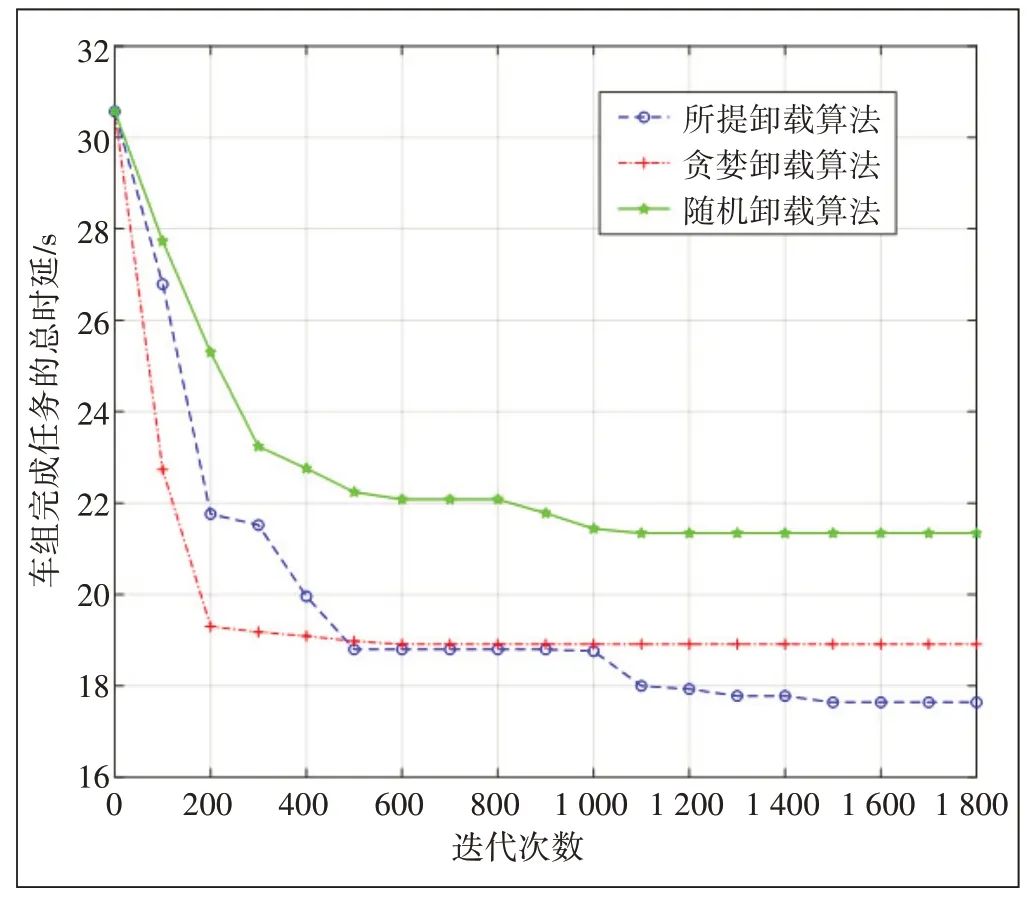
图4 N=135时车组总时延随迭代次数增加的变化

图5表示车组的总任务时延随车组内子任务数量增加而变化的情况。固定车组行驶速度18 m/s，可以看出，3 种任务分配算法得到的车组总时延均会随车组内子任务数量的增长而增长。随着子任务数量增加，在子任务数量超过100以后，贪婪算法的增长速率要明显高于本文所提算法，这是因为子任务数量越多，贪婪算法越容易陷入局部最小，从而导致车组总任务时延较大。

图6显示了计算资源的利用率与组内车辆数量的关系。将计算资源的利用率定义为参与计算的车辆的平均计算时延与任务总完成时延之比［19］。计算资源利用率越高也即意味着每一个参与计算的车辆节点的计算时间越接近。从图6 可以看出，当车组中车辆数增加时，车组的计算资源利用率随之增加，这是因为，当参与任务的车辆越多，任务就可以在更短的时间内完成，所以离开车组的车辆返回结果所需的时间就越短，对整个车组的影响就更小。从图6 的结果可以看出本文所提算法与其他2种算法相比能更合理地分配任务，提高计算资源的利用率。

图7表示车组总任务完成时延随车速增加而变化的情况。从图7可以看出车组的总任务完成时延随着车组速度的增加而增加。因为车组行驶速度越快，车组在任务进行过程中通过的RSU 单元越多，离开车辆组的车辆返回的任务结果所经过的RSU 就越多，任务结果返回到车辆组的时间也就越长。

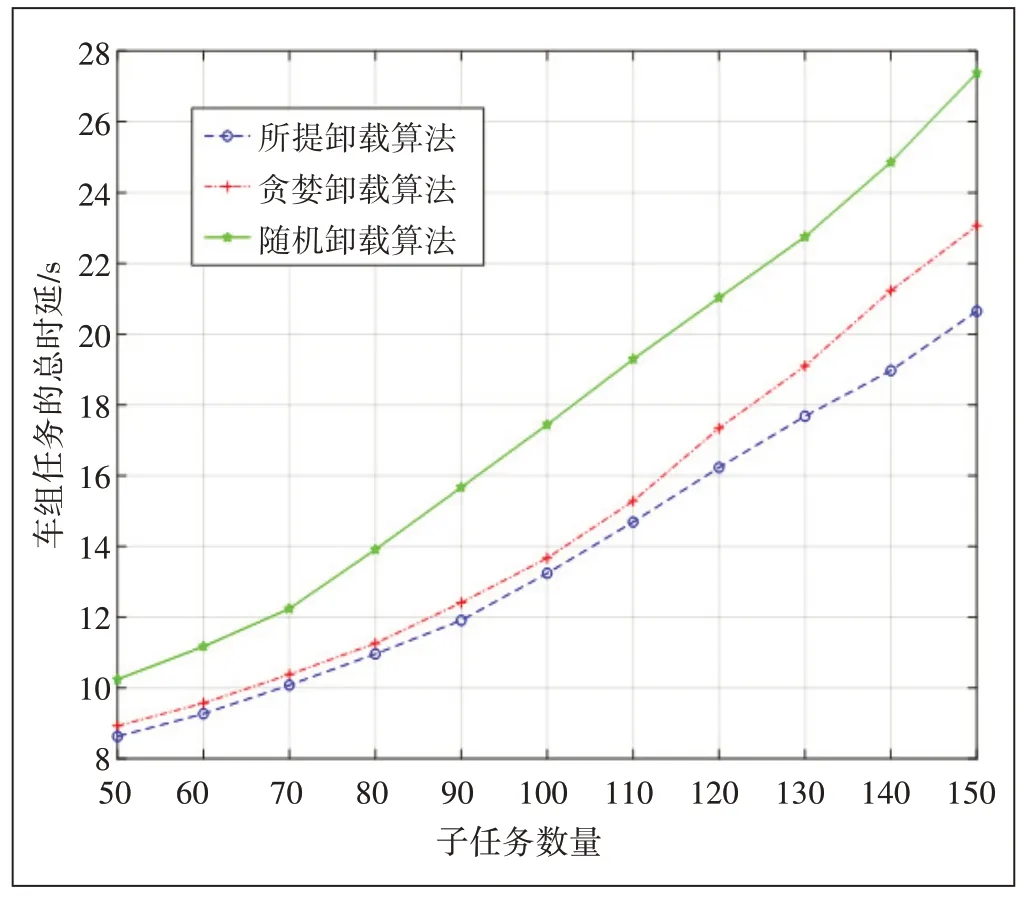
图5 车组平均任务时延随子任务数量的变化

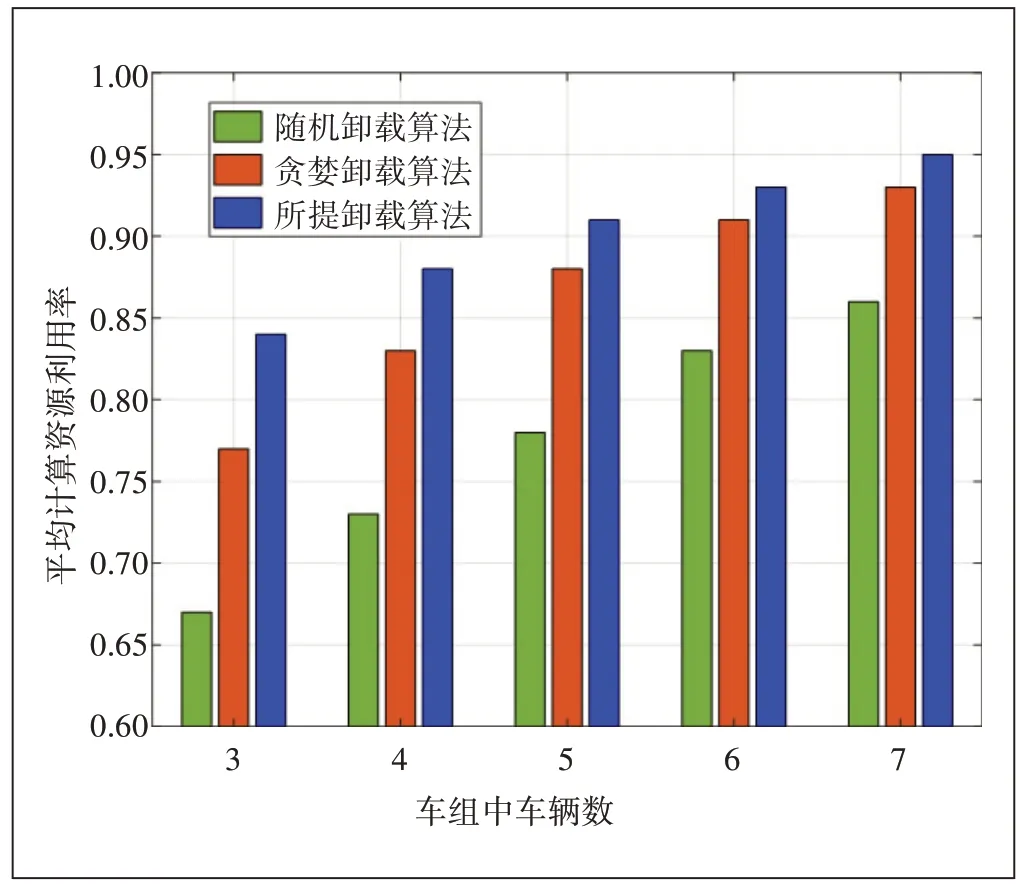
图6 车组平均计算资源利用率随车辆数增加的变化

4 结束语

本文对基于车辆成组的组内V2V 计算任务卸载问题进行了研究，提出了一种考虑车辆在计算卸载过程中离开车组的任务分配算法。首先介绍了研究背景与网络模型。然后联合考虑车组成员能保持稳定连接的时间和车辆因故障突发离组的情况，具体分析了车辆离组的2种情形并建模。将计算任务划分成不同类型的子任务，并设计了一个动态的组内计算任务分配算法。该算法调整了子任务的分配方式，通过迭代实现总时延最小。最后，通过仿真对所提算法的有效性进行了验证。

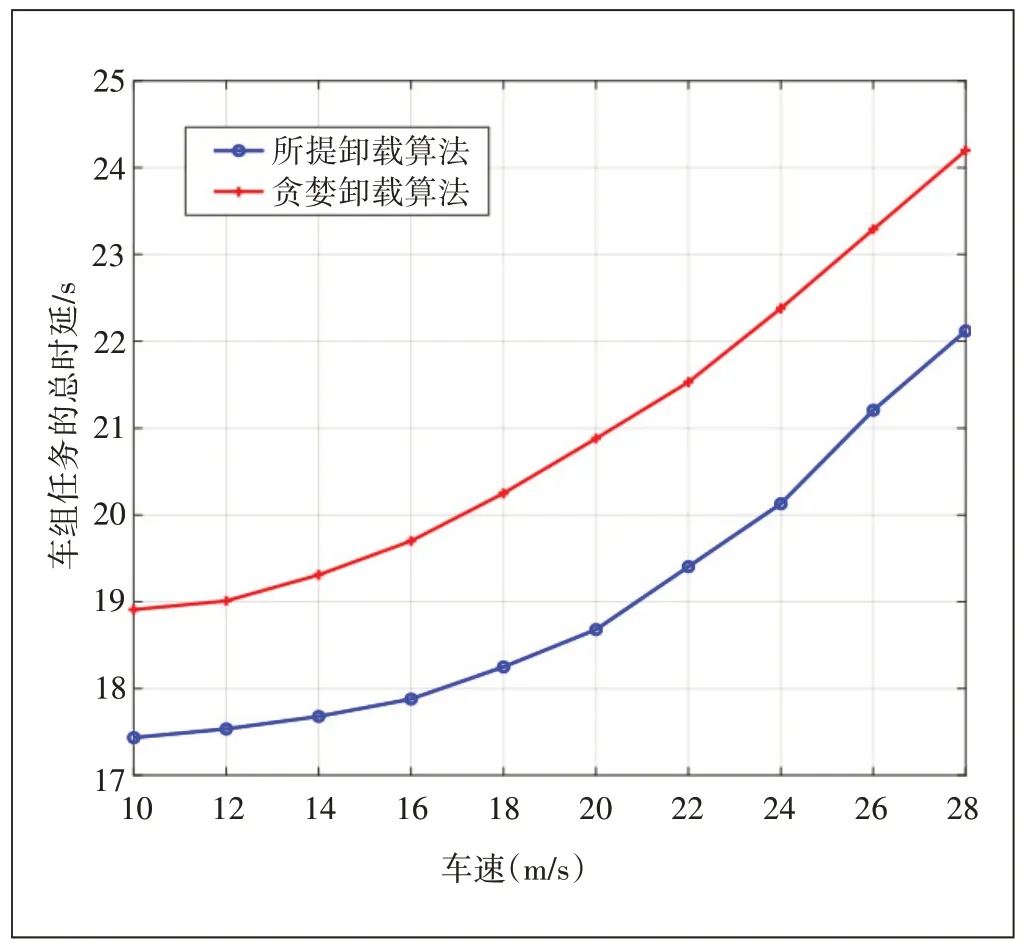
图7 车组总时延随车速的变化