损伤叶片动力参数变化规律的数值模拟与试验研究

顾永强，冯锦飞，贾宝华，张哲伟

（内蒙古科技大学 土木工程学院，内蒙古 包头014010）

运行状态下的风机叶片由于工作环境多变复杂以及运行时产生的振动和变形导致损伤从而影响风机的平稳运行[1-2]。因此针对叶片的损伤检测成为了研究热点。在目前众多的损伤识别方法中，结构的自振频率具有测量精度高、测量方法简单等优点，从而成为了结构损伤识别中最方便也是最常用的一种方法。此外，自振频率是结构的特有属性，与测量传感器个数以及测点位置无关，这就使得测量点可以根据工程实际进行设置，这些均是基于自振频率进行损伤识别被广泛应用的原因。Patil 和Maiti[3]采用结构固有频率的损伤识别方法对梁型结构进行了多裂纹试验数据研究。谢峻和韩大建[4]在前人的基础上对频率损伤识别方法加以改进并以此对钢筋夯的三跨连续梁进行有限元模拟。王乐等[5]通过建立结构固有频率与损伤值的数据库，并采用最大置信准则判断结构是否发生损伤。李录平等[6]利用有限元软件ANSYS 对损伤前后的风力机叶片进行模态分析，得到其固有频率和振型，通过计算出损伤前后的1阶模态应变能以及损伤前后单元模态应变能改变率的变化情况，可对结构进行损伤诊断和定位。在目前运用振动方法进行结构的损伤识别时，对叶片固有频率有较大影响的因素如转速等基本采用有限元分析或者数值模拟的方法，虽然其分析的结果对叶片研究具有重要的参考意义，但数值分析的结果和实际情况相比还是会有很大的不同[7]。本文通过对某小型风力发电机叶片从试验与模拟两方面出发，研究在损伤与动力刚化工况下叶片固有频率的变化规律，并提出了损伤识别的方法，用于损伤位置的定位与确定损伤的程度。

1 风力发电机叶片理论分析

1.1 叶片损伤理论分析

叶片的振动力学方程如下：

其中：[M]为质量矩阵、[C]为阻尼矩阵、[K]为刚度矩阵、[x]为位移列阵[f(t)]为激励列阵；

一般结构体系的阻尼比ζ比较小，可忽略不计,当不受外力时式（1）有非零解，即自由振动状态[8]。此时，叶片的自由振动方程如下：

设x=[ψ]eωx，[ψ]为N×1 阶自由振动的幅值阵列则频域方程可写为

此时ω2看作为特征值γ，ψ看作特征向量，所以γi是特征值，ψi是第i阶归一化的位移模态向量，则：

当叶片发生损伤时，进而结构刚度矩阵就会的改变，相应的γi及ψi也会发生改变，叶片的损伤振动变化方程为

式中：[αK]、αγi、αψi分别为结构刚度矩阵、特征值、特征向量的变化量。

式（4）、式（5）联立得：

用ψTi乘以式（6）联立式（4）可得：

当叶片发生损伤后其刚度减小即[αK]≤0，所以αγi≤0，又因为γ=ω2，因此，由αωi≤0 可看出叶片的损伤会导致其频率减小。

1.2 损伤识别理论分析

与固有频率或位移模态模态相比，模态柔度对局部损伤更敏感。针对面式悬臂梁结构，通过频率矩阵和振型矩阵在模态满足质量归一化的条件下构成柔度矩阵函数，如式(8)所示，本文采用加权柔度曲率作为损伤识别指标，计算如下。

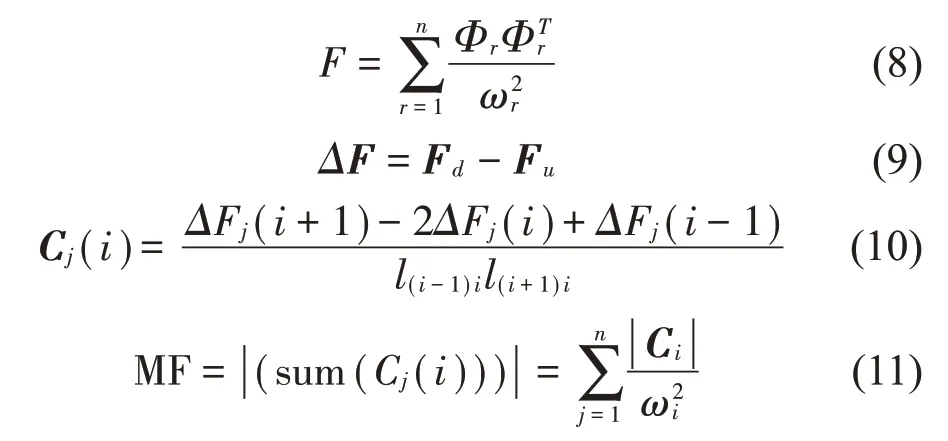
式中：F为模态柔度；Fd、Fu为损伤前后柔度矩阵；ΔF为柔度差；Φ为振型；ω为频率；Cj(i)为柔度曲率；MF为加权柔度曲率。

2 损伤风机叶片的研究

2.1 叶片模型的建立及损伤单元设定

某小型水平轴风电机组叶片长1.55 m，叶尖处7.5 cm，叶片最宽处23.5 cm，蒙皮厚4 mm，材质为玻璃钢，弹性模量为1.1 GPa，密度为7 800 kg/m3，泊松比为0.22。模型采用壳单元，边界条件为叶片根部固定，通过对叶片具体尺寸进行测量并建立有限元模型如图1所示。

图1 叶片有限元模型

通过采用降低弹性模量的方式来模拟风机叶片的的局部损伤。设损伤前单元弹性模量为E，损伤后为E′，损伤程度：

本试验选择距离叶片根部20 cm、40 cm、60 cm以及80 cm处的位置通过对伤口面积的增大模拟不同程度的损伤，如图2所示。共4 处位置8 种工况，具体损伤情况如表1。

图2 损伤位置标定

2.2 风机叶片的动力特性试验

测试设备有：XJP 数字显示仪、信号放大器、采集仪、加速度传感器等。本次试验共有9个叶片，叶片的材料都采用玻璃钢纤维复合材料制作，叶片长1.55 m 叶尖处7.5 cm，叶片最宽处23.5 cm。叶片夹在万能试验机上，其根部约束相当于固定端约束。如图3所示。

表1 损伤单元的设定

图3 叶片与端部约束

通过人为打磨叶片表面来降低局部刚度代替叶片损伤，位置距离叶片根部分别为20 cm、40 cm、60 cm、80 cm 处。如图4所示。共4 处位置8 种工况，具体与表1相同[9]。

图4 叶片损伤位置图

2.3 静止状态下模拟与试验结果对比分析

在ANSYS 中对所有工况下的叶片进行模态分析提取前2阶频率值。对试验所用叶片迅速敲击叶片测定其前2阶频率。频率值采用单叶片测三组求平均值的方法确定。首先分别测量叶片无损情况下的频率值如表2所示。

首先对比模拟数据与实验数据在相同的损伤程度下（本文模拟数据选取20%，试验数据选取损伤面积1.3 cm×8 cm）随着损伤位置的频率变化规律，结果如图5所示。

表2 无损叶片固有频率值/Hz

图5 损伤叶片频率与位置关系图

由图5可得，对不同位置同一损伤大小进行比较，不论是有限元模拟还是试验，损伤后的叶片频率与损伤位置呈线性关系，即越靠近根部叶片频率下降越多。其次，对比模拟与试验在同一位置处不同损伤大小工况下的频率变化规律，结果如图6所示。

由图6可知，无论是模拟数据还是实验数据，在同一位置处不同的损伤大小工况下，1阶频率与2阶频率改变的趋势基本相同，皆为损伤越大频率下降得越多。

2.4 旋转状态下模拟与试验结果对比分析

叶片在旋转的过程中，叶片刚度会由离心力与重力沿着叶片轴向的分力之和提供，由此导致刚度增大，最终使得结构的固有频率增大，这便是动力刚化效应。因此，最后通过对比模拟与试验在旋转工况下损伤叶片的频率变化规律确定动力刚化效应对叶片频率的影响。结果如图7、图8所示。

由图7、图8可知不论是模拟还是试验，叶片是否发生损伤，随着叶片转速的提高，其固有频率都会随之增大。叶片发生损伤时刚度下降，从而其固有频率减小。但是由于动力刚化效应的影响，其频率会增大，此时会给损伤检测带来识别困难。

3 损伤位置的识别与损伤程度的检测

在模态满足质量归一化的条件下，柔度矩阵是频率矩阵和振型矩阵的函数。由式(7)可知，利用模态柔度对结构进行损伤识别时，只需少数低阶模态就即可满足要求，无需测得高阶模态。因此，取各单元前3阶频率与振型进行计算分析。本文取损伤工况如表3所示。

图6 同一位置处不同损伤程度频率对照图

图7 模拟叶片旋转前2阶频率变化图

图8 旋转试验条件下的叶片频率变化图

表3 叶片损伤工况表/(%)

模拟叶片跨中单元8号损伤以及单元4号损伤，损伤量为刚度分别下降20%、40%、60%、80%，计算MF 值得到与结点号的对应关系如图9所示。由图可知，在损伤结点处，加权柔度曲率值远大于其他无损位置处，呈凸起状。且随着损伤程度的增大，在损伤位置处的MF值也在变大。

4 结语

通过对试验结果与模拟结果进行对比，得出以下几个结论：

(1)叶片发生损伤后其自振频率与损伤前相比较均下降，且随着损伤程度的不断增大，频率值下降越多。因此，通过自振频率的变化可对叶片是否发生损伤进行判断。

(2)通过叶片自振频率与转速的关系图可知，叶片绕轮毂旋转时产生的动力刚化效应使得叶片固有频率值随着转速的增加均呈上升趋势。且随着转速的增加，自振频率改变率逐渐降低，说明其损伤识别的敏感性逐渐下降。

(3)风电机组叶片发生损伤时，损伤位置处加权柔度曲率值的变化随损伤程度的加剧而呈上升趋势，且在损伤部位出现较其他部位更为显著的变化。因此，利用损伤前后加权柔度曲率值的变化可对叶片的损伤程度及损伤位置进行识别。

(4)自振频率的测试会受到外部环境的影响，因此实际应用自振频率进行损伤程度识别时，可能会对识别结果的精度产生一定影响。

图9 损伤识别结果