基于改进HHT和SVM的滚动轴承故障状态识别

王圣杰，殷 红，彭珍瑞

（兰州交通大学 机电工程学院, 兰州730070)

滚动轴承在旋转机械的运行中起着至关重要的作用，正确分析其故障是必要的，信号分析可以提前预测轴承故障模式，延长轴承的使用寿命[1]。

基于振动信号的故障诊断方法很多，Rai 等[2]综述了不同信号处理方法在滚动轴承故障诊断中的应用。经验模态分解（EMD）在旋转机械故障诊断中被大量使用[3]，Yang 等[4]采用EMD 对轴承振动信号进行分解将其分解为一系列固有模态函数（IMF），然后计算敏感模态函数的特征幅值，将其作为故障特征向量输入支持向量机（SVM），用来诊断滚动轴承的故障状态。EMD 容易发生模态混叠现象，Wu和Huang[5]在EMD的基础上改进提出集合经验模态分解（EEMD）。于德介等[6]将Hilbert-Huang 变换（HHT）引入齿轮故障诊断中，将局部Hilbert 能量谱与支持向量机结合实现故障模式识别。张超等[7]将EEMD分解后IMF分量的能量特征输入SVM，判断齿轮的工作状态和故障类型。EEMD与Hilbert相互结合的方法在故障诊断领域使用较多[8-9]。

多分类SVM在故障诊断中大量使用，但其参数的确定影响整个分类效果[10]。吴景龙等[11]利用遗传算法（GA）优化SVM参数实现轴承状态识别。轴承特征向量组成高维数据集，它可以更广泛地揭示原始信号的固有属性，但也带来了一些冗余和负面的特征信息，特征维数越高，分类的耗时越长[12]。因此，需要在多域特征提取后对高维特征向量进行降维处理。He 等[13]提出拉普拉斯得分（Laplacian score，LS）特征降维方法，基于每个候选特征的重要性来评估和选择有意义的敏感特征子集。

采用EEMD提取反映振动信号局部特性的IMF分量，通过相关系数删除原始数据集中的冗余特征与噪声特征，计算筛选出IMF 分量的Hilbert 边际谱能量值与Lempel-Ziv 复杂度值，由此构造轴承的初始状态特征量，采用LS逐维评价特征对于反映轴承状态数据的作用，挖掘对改善分类性能更有效的特征。利用得到的特征向量对SVM进行训练，实现轴承故障状态的自动识别。

1 数据特征提取与降维

1.1 Hilbert边际谱能量

HHT 的核心是通过EMD 将信号分解为若干IMF 分量，由于EMD 分解信号会产生模态混叠现象，应用EEMD对信号进行分解。改进HHT过程首先利用相关系数R筛选EEMD分解后含轴承故障信息量较大的IMF 分量；再对每个IMF 进行Hilbert 变换，得到相应的Hilbert谱，最后对其进行时间积分求取Hilbert边际谱。

EEMD 对传感器采集的轴承连续时间信号x(t)进行分解，得到一系列IMF分量与一个余项，对每个IMF 分量imfi(t)进行Hilbert 变换，可得Hilbert 谱，记为

式中：RC 表示取实部运算；Ai(t)为瞬时幅值；Fi(t)为瞬时频率。

Hilbert边际谱h(F)定义为

Hilbert边际谱能量E(F)定义为

式中：F1、F2为Hilbert边际谱h(F)的频率区间。

Hilbert边际谱表示信号幅值在整个频率段上随频率的变化情况，与傅里叶谱相似，但比傅里叶谱具有更高的频率分辨率。Hilbert边际谱能量增强了轴承故障信号中的频率成分，抑制了噪声的干扰影响。

1.2 Lempel-Ziv复杂度

Lempel-Ziv（全文简称L-Z）复杂度由Lempel 和Ziv提出，物理意义在于反映信号时间序列随着序列长度的增加出现新模式的速率，复杂度越大，出现新模式的速率越快。主要计算参见文献[14]。

单独以IMF分量的Hilbert边际谱能量或L-Z复杂度为特征向量时，所提取的轴承特征向量只从信号频率或时间层次出发对轴承故障进行识别，识别率较低，为此考虑从时间与频率两个角度提取轴承信号的特征向量，同时计算IMF 分量的L-Z 复杂度和Hilbert 边际谱能量组成复合特征向量，再对轴承不同故障状态进行识别。

1.3 特征降维

LS 基本思想是根据特征的局部保持能力来评价特征的重要性。给定m个数据样本，每个数据样本包含n个特征。假设Lr为第r个特征的LS，r=1,2,…,n，令fri为第i个样本对应的第r个特征，i=1,2,…,m。

（1）构建样本的最邻近图G

当两个样本xi,xj,i≠j较“近”时，将两个样本通过边相连。可以取xi的k邻近点，建立最近邻近图。

（2）计算相似度矩阵S

式中：T为合适的常数。

（3）计算图的拉普拉斯矩阵L

对于第r个特征，fr可以定义为

式中：矩阵L被称为图拉普拉斯变换。

第r个特征的拉普拉斯积分可以计算如下：

式中：Var(fr)为第r个特征对应的方差。

LS 计算公式是由特征样本间相似度之和与该特征样本间的方差之比得到的。Sij值越大，Laplacian 分数Lr越小，特征重要性越高，也就是说，一个好的特性的LS 值很低。因此，选取前几个LS 值较小的特征作为包含几乎全部故障信息的敏感特征，可以去除冗余信息，提高计算效率。在此基础上，利用LS算法对提取的多域特征建立新的低维特征集。

2 GA-SVM模式识别模型建立

SVM是一种小样本学习方法，用“一对一”的方法进行SVM多分类。核函数的选择是SVM分类方法的关键，本文选用径向基函数（RBF）。由于篇幅问题，不对SVM 具体内容进行论述，详细参考文献[11]。

GA-SVM模型的基本步骤如下：

(1)GA 和SVM 的参数设置。其中惩罚因子C和核函数g的范围分别为[0,100]和[0,1 000]。

(2)根据提取出的轴承特征向量，划分训练集和测试集。对最初的故障特征集进行归一化处理：

式中：xmin与xmax分别为特征向量数据序列中的最小值和最大值。

(3)将训练集特征代入SVM 模型中，获得种群的适应度。进行选择、交叉、变异操作，在最佳适应度下选择C和g。

3 基于EEMD-Hilbert和GA-SVM的滚动轴承故障诊断

轴承特征提取和SVM 的参数选择对于轴承的状态识别来说相当重要，而特征提取和SVM参数的合理选择将直接影响分类的诊断精度和计算时间。EEMD 方法能够将信号分解为若干个IMF 分量，可以解决EMD分解中存在的模态混叠问题。基于此，将EEMD-Hilbert和GA-SVM相互结合，对轴承不同状态进行识别。滚动轴承故障状态识别流程图见图1。具体步骤如下：

1）利用传感器采集轴承不同故障状态时的原始信号，再对故障信号进行分组；

2）采用EEMD分解信号，将原始信号分解得到一系列IMF分量；

3）计算IMF分量与原始信号的相关系数，筛选含故障信息量较大的IMF分量；

4）从时域与频域内提取轴承信号的特征向量，从时间序列角度，提取IMF分量的L-Z复杂度值，从频域角度对IMF 分量进行Hilbert 变换，提取IMF 分量的边际谱能量，两者组成轴承不同状态的特征向量；

5）计算特征向量的LS，选出最能分辨轴承数据局部结构的特征向量；

6）将训练集数据带入GA-SVM进行训练，获得C和g最优时的模型，将测试集数据输入此模型进行分类，完成滚动轴承的故障状态识别。

图1 滚动轴承故障状态识别流程图

4 算例

为验证本文所用方法的有效性，采用美国西储大学实验室采集的滚动轴承实验数据，选取轴承的10种状态故障样本[9]，具体数据如表1。轴承10种故障状态分别为轴承正常工作状态，以及轴承内圈、滚动体和外圈在3种不同损伤程度下发生的故障状态组成。其中外圈故障选择发生在6点钟方向损伤时故障数据，3 种损伤直径为0.178 mm、0.356 mm、0.533 mm。其采样频率和转速分别为12 kHz 和1 797 r/min，截取每段信号中50组数据，每组数据连续且样本点数为2 048。

轴承10种状态下的时域波形图如图2所示。

相关系数R定量地刻画了X和Y的相关程度，即R越大，相关程度越大。以轴承内圈故障为例，分别计算EEMD分解后各IMF分量与原始振动信号的相关系数R，结果如表2所示。

由表2可知，IMF1～IMF8与原始振动信号的R较大，则EEMD 分解后前8 个IMF 分量与原始振动信号相关性较强；对其进行Hilbert变换，得到的Hilbert边际谱如图3所示。

表1 轴承10种故障状态样本

根据Hilbert 边际谱能量与L-Z 复杂度计算公式，分别计算R筛选出IMF分量的特征向量，计算出轴承4种状态的Hilbert边际谱能量与L-Z复杂度进行故障辨识。IMF1分量的Hilbert边际谱能量与L-Z复杂度，如图4所示。

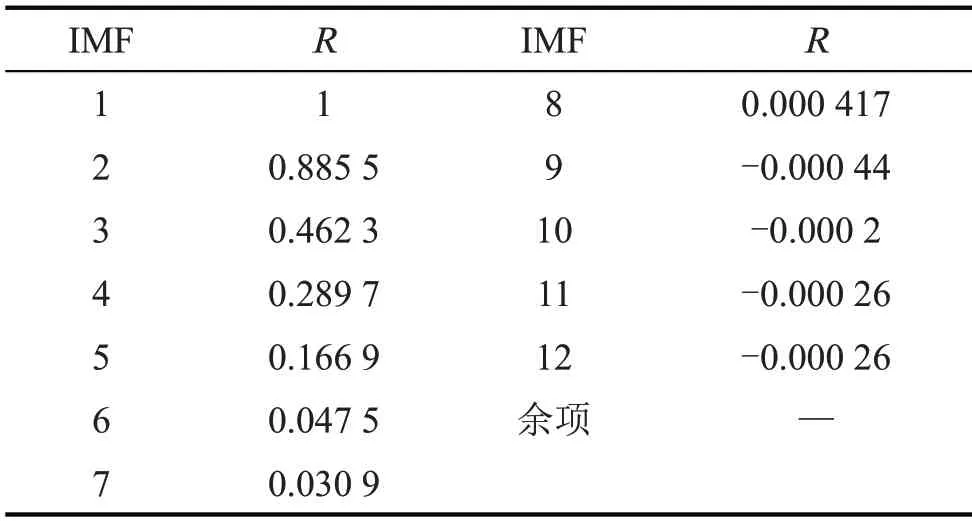
表2 IMF分量与原始振动信号的相关系数

由图4显示出滚动轴承不同故障类别之间以Hilbert边际谱能量与L-Z复杂度作为特征向量时有显著差异。因此，上述两特征量可区分出滚动轴承的故障类别。

图2 滚动轴承不同故障状态下时域图

图3 IMF1～IMF8的Hilbert边际谱

轴承10 种状态下，每种状态50 组数据，共500组数据；每组数据经EEMD分解，利用R计算前8个IMF分量的Hilbert边际谱能量与L-Z复杂度组成特征向量，每组数据共16 个特征向量；最后构成一个高维的时频域特征集大小为500×16。在此基础上，引入LS 从高维特征集中对敏感特征进行评价和选择。根据不同特征的重要性及其与主要故障信息的相关性，对其重新排序。

为了分析LS 算法的贡献以及Hilbert 边际谱能量与L-Z复杂度组成的复合特征向量的适用性，图5给出了LS 算法在不同特征向量（Hilbert 边际谱能量、L-Z 复杂度、复合特征向量）在不同维度下的诊断识别率和运行时间。

从图5中可以看出，单独以Hilbert 边际谱能量或L-Z 复杂度为轴承特征向量时，无法实现在最短时间内达到较高诊断精度。本文采用的LS 算法选择8 维特征集组成的复合特征向量，在运行时间较短的情况下，可以得到较高的诊断识别率。

为进一步验证LS 算法的有效性，将LS 算法与数据方差进行比较。将挑选的轴承特征向量作为GA-SVM 分类器的输入，获得分类精度。图6描述了两者在不同特征维数的识别率。

从图6可以看出，在特征维数小于11的情况下，使用LS 算法得到的识别率明显高于数据方差。因此，本文采用LS 算法进行轴承状态特征选择是有效的。

最后将LS 筛选出的特征向量重新组合得到的低维特征集加入到GA 优化后的SVM 分类器中，实现滚动轴承故障模式的自动识别，程序迭代5 次。图7为当惩罚因子C 和核参数g 分别优化为0.837 2和5.024 9时，SVM分类器对轴承不同故障状态的识别结果。轴承10种状态除滚动体3的分类识别率为90 %（18/20），其余状态的识别率均为100 %（20/20），轴承整体数据样本的分类识别率为99%（198/200）。

4.1 不同模型的故障诊断效果对比

图4 EEMD分解IMF1分量的Hilbert边际谱能量与L-Z复杂度值

图5 在不同特征维数下的分类性能

图6 不同特征选择方法的诊断准确性

图7 本文所用方法分析结果

用人工鱼群算法（AFSA）和粒子群算法(PSO)与GA优化SVM参数进行对比。输入相同的特征样本，IMF分量的Hilbert边际谱能量，各算法初始种群数都为20，最大迭代次数为200。将上述处理好的训练集和测试集输入构造好的模型，进行结果分析，如表3所示。（其中：POM-SVM参数优化方法；RT-运行时间（s）；SR-识别率）。

而患有哮喘、严重高血压、Ⅱ度房室传导阻滞或其他无法使用压力导丝的冠状动脉狭窄患者，对QFR风险的容忍度较高，使用QFR会提供冠状动脉功能性评估信息，患者可获得明显收益。

表3 Hilbert边际谱能量

表3为选取EEMD 分解后利用相关系数R选出的前8个IMF分量的Hilbert边际谱能量代入不同算法优化的SVM 中，其分类效果差别较大，在时间和分类正确率上GA 优化SVM 参数的平均时间只要59 s，且识别率较高，说明GA能够实现快速、准确地对SVM参数优化，构建的轴承状态识别模型能够准确地进行故障诊断。

4.2 不同特征向量的故障诊断效果对比

为验证Hilbert边际谱能量值与L-Z复杂度值相结合作为特征向量进行轴承状态识别的合理性，运用不同的特征向量输入到GA-SVM分类器中，对轴承故障进行分类，分类效果如表4。

表4 不同特征向量分类效果

从运行时间和识别率两方面观察不同特征向量的识别效果，表4和图8可看出，Hilbert 边际谱能量值与L-Z 复杂度值在轴承状态识别中比能量熵、奇异值熵、峭度为特征向量时，运行时间较短并且识别率较高。文中将两者结合组成轴承复合特征向量，识别率为99%，比单独使用Hilbert边际谱能量值或L-Z 复杂度值作为轴承特征向量时，状态识别率得到了明显提升。

图8 不同特征向量下的分类识别率

5 结 语

考虑从时间与频率两个角度提取轴承信号的特征向量，采用改进的HHT方法提取轴承不同状态下IMF分量的Hilbert边际谱能量并计算IMF分量的LZ 复杂度，两者可以很好地反映轴承不同状态下振动信号的特征量。