基于经验模式分解和排列熵的轴承故障特征提取

王 涛，胡定玉，丁亚琦，廖爱华，师 蔚

（1.上海工程技术大学 城市轨道交通学院，上海201620；2.上海地铁维护保障有限公司 车辆分公司，上海200235）

滚动轴承作为减少摩擦损失的精密元件，被广泛用于旋转机械中，但高速重载的环境导致轴承极易发生故障，影响列车的安全出行，因此对轴承的运行状况检测十分必要。当滚动轴承出现故障时，内外滚道与滚动部件之间发生碰撞，会产生一个强迫短脉冲信号，通过对这些信号进行分析可以有效检测故障从而减少事故的发生。与传统的振动分析相比，采用声信号监测轴承的健康状况更加方便快捷，无需粘贴传感器，与检测对象相互独立，该方法对轴承早期故障的检测也有较好的效果。

传统的时域与频域分析方法难以有效分析轴承故障信号的时变特性，无法准确体现其故障特征。针对该类信号，通常采用小波分解[1]和经验模式分解[2]等时频分析方法。时频分析将时频两域结合起来，可以同时考虑到两个域的性能；在时频相平面上可以精确地定位出某一时刻出现了哪些频率分量。小波分解在分析信号之前设置一些参数（小波基函数），将信号分解成不同频率范围的子信号[3-4]，不同的小波基会产生不同的分解结果，最佳小波基的选择成为了较大的难题。经验模态分解（EMD）[5]可以自适应地将信号分解为固有模态函数和残差，可以对不同的分量进行独立分析[6]。

目前EMD 已在滚动轴承故障诊断领域广泛应用，杨世锡等[7]将经验模式分解和Hilbert 变换引入旋转机械的故障诊断中，并与小波时频分析相比较，研究结果表明基于EMD 的Hilbert 变换具有更好的效果，但出现了一些虚假分量；张志刚等[8]提出一种改进经验模态分解和谱峭度相结合的算法，剔除了分解过程中出现的虚假分量，但缺点是其受噪声影响较大。

本文提出一种基于经验模式分解和排列熵的轴承故障分析的信号处理方法，为EMD分解后IMF分量的选择提供了新的方法。首先介绍相关基础理论，然后通过数值仿真与传统的包络分析进行比较，最后通过实验数据的分析验证该方法的有效性。

1 基础理论

1.1 经验模式分解算法

EMD是一种自适应时频信号处理方法，通过对复杂信号进行分解，获得一系列用于表征原始信号特性的IMF 分量，筛选一些合适的本征模态分量实现对原始信号所包含的信息特征进行分析。分解出的IMF 必须满足以下两个条件[9-11]：(1)在所需分解的数据段中，极点数和过零点数的差值不能超过一个；(2)信号的任意时刻，由极大值点插值所构造的上包络线和极小值点构成的下包络线均值为零。

EMD的实施步骤如下：

(1)找出原始信号所有的极大值点和极小值点，利用插值的方法分别对极大值点和极小值点进行连接来拟合原始信号的波形，形成上包络线和下包络线。

(2)计算上下包络线的平均值m1，求得：

若h1满足上述条件，则为信号的一个IMF分量，记为IMF1，进入下一个循环。

(3)若h1不满足条件，则用h1替代初始数据x(t)，重复步骤(a)、(b)，得到h2，并判断h2是否满足(b)的条件，若还是不满足条件，则继续循环迭代直到获得满足条件的IMF1分量。

(4)将IMF1分量从信号x(t)中分离出来，得到新的循环信号：

(5)将R1作为原始信号，重复步骤(1)～(5)，当Rn的极值点数小于2，则循环结束，得到n个IMF 分量和残余分量Rn，信号x(t)可表示为

在EMD的分解过程中，由于需要人为设置迭代次数和终止条件，因此会产生一些无关信息成分，即虚假分量。针对该问题，可以利用相关系数来识别虚假分量[12]。

1.2 排列熵算法

排列熵作为描述复杂系统的算法，对突变的信号较为敏感。当滚动轴承系统发生故障时，声信号包含的冲击成分，会对排列熵值造成影响，因此可以利用排列熵对轴承进行早期故障诊断。

给定一个序列{X(K),K=1,2,…,N}，对其进行相空间重构得：

其中：d为嵌入维数，τ为延迟时间，k为重构分量。对矩阵Z中的每一行序列进行升序排列：

式中：t表示索引的列数，R1,R2,…,Rd为X(K)中各元素所处的位置。定义xdi为重构后的任意一组序列，0 ≤Ri≤d!，对于d维相空间映射有d!种排列的可能性，计算每一种序列出现的可能性P1,P2,…,Pi，对于时间序列X(K)的i种排列熵Hp(d)：

当Pi=m!时，Hp(d)就达到最大值In(m!)，为了方便熵值的比较，往往会对排列熵值进行归一化处理：

Hp的值越小则表示该序列越有序，反之该序列的复杂程度越高。由于发生故障的轴承元件在运行过程中与其他元件发生周期性的冲击，相较于正常轴承信号，故障信号更加有序，排列熵值较小。因此可以用排列熵值的突变来判断轴承是否发生故障。

在计算排列熵时，插入维数d过小会导致重构信号状态量缺失，对冲击信号的敏感性将大大下降，算法失去有效性；插入维数过大会使得信号在相空间的重构过程中均匀化时间序列，因而一般维数选择为3～7，本文取5，时间延迟τ=1[13]。

EMD将信号分解为多个IMF分量，高频IMF分量中包含较多冲击成分，但包含大量噪声，低频IMF分量噪声成分较少，但可能是虚假分量。为筛选本征模态分量中包含信息量较大的真实分量进行信号的重构，可以利用排列熵值和相关系数来作为筛选指标。排列熵值Hp与原始信号的有效成分呈反相关，相关系数r与原始信号的线性相关程度呈正相关。基于此本文提出联合系数Co作为IMF 分量的筛选指标，取联合系数最大的前两个本征模态分量进行信号的重构：

1.3 快速谱峭度算法

谱峭度为能量归一化的4 阶谱累积量，利用计算每根谱线的峭度值来反映瞬时冲击的大小，快速谱峭度(Fast-kurtogram)则以STFT作为窗口，根据快速谱峭度图选择最佳滤波参数。

在信号x(t)的激励下系统响应y(t)Wold-cramer分解的频域表达式为

其中：H(t,f)为y(t)在频率f处的复包络信号。y(t)的四阶谱累积量为

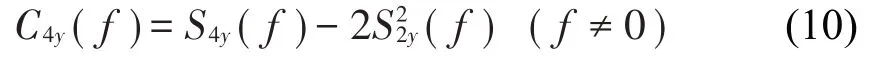
式中：S2ny(f)为2n阶谱瞬时距，用以表示复包络信号的能量大小，定义为

式中，df表示对频率f求导。谱峭度定义为

为减少运算时间，可以应用于实际的工程测量，采用塔式快速谱峭度对信号进行2倍频采样滤波迭代，将原信号进行L层滤波分解，每层滤波后的信号频段为2L个，一般情况下L为整数。为了提高信号分解的精度，在L+1 层和L+2 层中插入3×2L个滤波器，即L+1.6层，如当L=0时，第1层和第2层之间分解层数为1.6层时，表明该层将原始信号分解为3个信号频段。根据快速谱峭度图上峭度值的大小，即颜色最深的频段选取最佳滤波中心和滤波带宽，进行平方包络分析和故障提取。

2 EMD-PE故障诊断方法流程

应用快速谱峭度算法诊断轴承故障虽然取得了一定的效果，但对信号进行预处理可以进一步提高诊断效果，本文将EMD 和排列熵值相结合，提出一种基于声信号滚动轴承故障诊断的EMD-PE 方法，可以有效降低噪声的干扰并确定合适的滤波器参数。该方法流程图如图1所示。具体过程如下。

(1)对原始信号进行EMD分解，把非平稳、非线性的声信号分解为8 个本征模态分量IMF1，IMF2，···，IMF8。

图1 EMD-PE诊断故障轴承流程图

(2)计算各个本征模态分量的排列熵值Hp1，Hp2，··· ，Hp8(0 ＜Hpi＜1)和相关系数r1，r2，··· ，r8(0 ＜ri＜1)；

(3)计算联合系数，根据联合系数最大原则，筛选系数值最大的前两个本征模态分量进行信号的重构。

(4)对重构信号进行快速谱峭度分析，根据峭度最大化原则选择最佳滤波中心和滤波带宽。

(5)将从中提取到的轴承特征频率与理论故障特征频率对比，进行故障诊断。

3 轴承故障信号仿真分析

为了证明该方法在滚动轴承故障诊断中的有效性，现对模拟的轴承故障仿真信号进行分析，设轴承发生单点局部故障，传声器接收到信号的信号数学模型为

其中：x(t)为轴承故障仿真信号，A为冲击信号幅值，s(t)为脉冲冲击函数，Ti为特征频率出现的周期，fs为轴承座、传感器系统的高频固有频率，ξ为幅值衰减系数，n(t)为高斯白噪声信号。

设仿真参数A=1，特征频率fi=1/Ti=130 Hz，固有频率fs=5 000 Hz，衰减系数ξ=1000，采样频率Fs=51200 Hz，采样点数N=10 240。仿真脉冲信号如图2(a)所示，对仿真信号添加高斯白噪声，SNR=10，如图2(b)所示。

对含有高斯白噪声的仿真信号进行EMD分解，对分解后的各个IMF分量进行排列熵值与相关系数的计算，并根据式(8)求得联合系数，如表1所示。根据联合系数最大化原则，筛选出两个最佳的IMF 分量(IMF6，IMF7)进行信号的重组，图3显示的是重组信号进行快速谱峭度分析得到快速谱峭度图。由图3可以看出，分解层数为1.6，带宽为8 333.33 Hz，滤波中心为23 333.33 Hz时，谱峭度值达到最大。在滤波后的平方包络图中，准确检测出了130 Hz 的特征频率及其倍频程如图4所示，这与预设的故障特征频率相符合，于是实现了故障的诊断，说明基于EMD 和排列熵的快速谱峭度的轴承故障诊断是有效的。

表1 仿真数据

图2 仿真信号时域图

图3 仿真信号快速谱峭度图

图4 基于EMD-PE算法的轴承故障仿真试验结果

4 实验分析

实验采用SKF 公司生产的滚动轴承故障实验台，故障轴承型号为SKF6016深沟球轴承,内圈存在一条裂纹，深约1 mm，其他部位保持完好，表2为该轴承的参数。采样频率是51 200 Hz，采样时间为10s，电机转速为404 r/min，转频为7 Hz，负载为5 N。

表2 滚动轴承参数

对于外圈固定，内圈转动的滚动轴承，其内圈故障的特征频率为

将轴承参数代入式(14)中可得轴承内圈故障特征频率为55.69 Hz。

声信号的希尔伯特包络变换的频谱图如图5所示，Hilbert频谱图中虽然可以得到故障频率，但却不够明显。

对信号进行EMD 分解，得到12 个本征模态分量，计算各个分量的排列熵值、相关系数以及联合系数，如表3所示，由于篇幅有限，这里只显示前8 个IMF的计算结果，其中原始信号的排列熵值为0.77。

由表3可知IMF4和IMF5的联合系数Co较大，原始信号中的突变特性成分较多，对IMF4和IMF5分量进行重组，得到的重组信号的排列熵值为0.29，相比于原始故障信号有用信息比例有所提高。

图5 转速为404r min时声信号的希尔伯特包络变换频谱图

表3 各IMF分量排列熵值、相关系数及联合系数

对合成信号进行快速谱峭度分析得到快速谱峭度图和平方包络图,如图6(a)、图6(b)所示。选取分解层数为4，带通滤波器的滤波中心18 000 Hz，而滤波带宽为1 200 Hz,在此滤波范围内峭度值达到最大，对滤波后的信号进行平方包络分析可以得到较为明显的滚动轴承内圈故障频率53.93 Hz 及其倍频，证明了本文方法的有效性。

图6 重构信号的快速峭度谱图和平方包络谱图

5 结语

本文提出了一种基于经验模式分解和排列熵的轴承故障分析的信号处理方法，利用联合系数代替了传统的峭度值，对IMF 分量进行筛选重构。此外针对滤波参数较难确定的问题，谱峭度对声信号中瞬态冲击较为敏感，可以自动确定带通滤波器的参数。经验模式分解和排列熵相结合的滚动轴承故障诊断方法，能够有效提取出故障特征频率及其倍频。仿真及实验结果验证了该方法的有效性。