非仿射多智能体系统的自适应神经网络控制
张 薇,余昭旭
(华东理工大学 信息科学与工程学院 自动化系,上海 200237)
0 引 言
多智能体系统因其在城市交通控制、无人机及机器人编队等系统中[1,2]的广泛应用受到了大量关注,而一致性问题是其中的研究热点。早期的研究主要集中在低阶确定性系统[3-7],但由于实际系统大部分为高阶不确定性系统[8,9],故需引入神经网络或模糊系统来处理系统的不确定性[10-12]。
反步法是处理具有下三角形式非线性系统的常用方法,但由于其容易造成“复杂性爆炸”问题[13],故引入动态面控制法来简化计算[14-18]。由于传统动态面法中边界层误差动态系统的未知非线性项没有得到补偿,控制性能会下降,故文献[19]提出了一种新的非线性滤波器来改善控制性能。
此外,实际系统中大量存在的未知控制方向情况也给控制设计带来了困难。目前,Nussbaum增益函数是解决控制方向未知问题最常用的方法[20],并已应用到多智能体系统中[21-23]。不过目前考虑的大多是仿射系统,而非仿射系统具有更一般的形式,可描述更为广泛的实际系统。但具有未知控制方向的非仿射系统所具有的特性也会增大控制策略设计的难度。
本文的研究对象是有向拓扑图下控制方向未知的非仿射非线性多智能体系统,并引入Nussbaum增益函数来处理由控制方向未知而带来的问题;利用RBF神经网络来处理系统的不确定项及耦合项;将新的非线性滤波器与反步法相结合来设计控制协议,最后通过一致性分析和仿真例子来验证所提出的控制协议的有效性。
1 问题描述及预备知识
1.1 图 论
有向图G={V,E,A} 表示智能体之间的信息交换,其中,V={v1,v2,…,vN} 是节点集合,E⊆V×V是边集。定义节点vi的邻居节点的集合为Ni={vi∈V|(vi,vj)∈E}。A=[aij]∈RN×N是邻接矩阵,其中aij≥0。 如果vj∈Ni, 则权值aij>0, 否则aij=0。 通常认为智能体无法从自身获得信息,即aii=0。 定义领导者的权值矩阵为B=diag{b1,b2,…,bN}, 若智能体i(i=1,2,…,N) 能从领导者获得信息,则bi>0, 否则bi=0。 通常假定至少存在一个跟随者与领导者有信息交流,即有b1+b2+…+bN>0。
1.2 RBF神经网络及其逼近
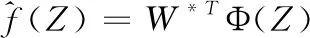
f(Z)=WTΦ(Z)+ε(Z), ∀Z∈ΩZ
(1)

引理1[24]假设RBF神经网络的基函数向量为Φ(Zb)=[φ1(Zb),φ2(Zb),…,φl(Zb)]T,Zb=[z1,z2,…,zb]T, 为其输入向量,则对任意的正整数a≤b, 有
(2)
1.3 系统描述
考虑一类由标记为0的领导者和分别标记为1,2,…,N的跟随者组成的多智能体系统,第i(i=1,2,…,N) 个跟随者的动态系统描述如下
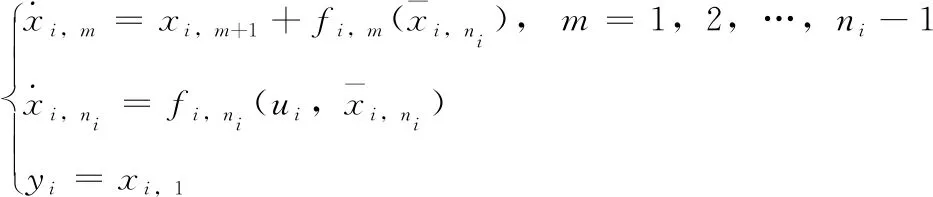
(3)
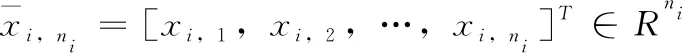
领导者的动态系统描述如下
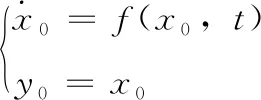
(4)
其中,x0∈R表示领导者的状态,y0∈R表示领导者的输出,且f(x0,t) 为连续有界函数。
注1:非线性系统(3)同时具有非仿射及非下三角的系统结构,可用来描述许多的实际系统,如船舶操纵系统、单杆机械臂及化工过程等。
本文的控制目标是设计分布式自适应控制协议ui,使得在有向网络拓扑下的多智能体系统中,各跟随者(3)的输出能与领导者(4)的输出同步,并且能够保证同步误差在零点的小邻域内。
为了实现以上控制目标,引入下列定义、假设和引理:

假设1[24]:有向图G包含一个领导者作为根节点的生成树。另外,第i个跟随者只能获得与其相邻的智能体的状态信息。
根据文献[24],假设1表明通过设计适当的分布式控制协议,第i(i=1,2,…,N) 个跟随者的输出yi可以实现与领导者的输出y0同步。
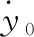
引理2[25]对于有向图G及领导者的邻接矩阵B,如果存在任意一个bi>0,那么L+B为非奇异矩阵。
引理3[25]对于有向网络拓扑G的多智能体系统,令z1=[z1,1,z2,1,…,zN,1]T,y=[y1,y2,…,yN]T和y0=[y0,y0,…,y0]T, 则有下式成立
(5)
其中,同步误差zi,1,i=1,2,…,N将在下文给出,且σmin(L+B) 为矩阵L+B的最小奇异值。
定义2[20]如果N(ζ)∶R→R是一个可微函数且具有如下特性,则称其为Nussbaum函数
(6)
(7)
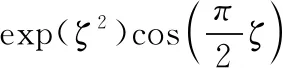
引理4[26]假设V(t) 和i(t)(i=1,2,…,N) 是定义在 [0,tf) 上的光滑函数,且对于任意t∈[0,tf), 都有V(t)≥0。 取Nussbaum函数为若有下列不等式成立
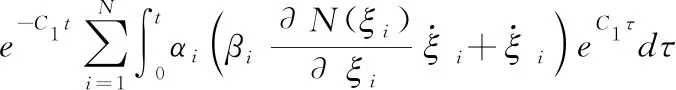
(8)
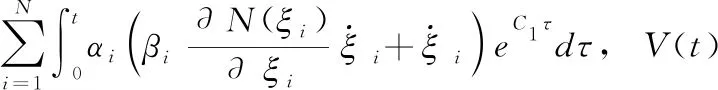

2 控制协议设计及一致性分析
本节将针对由式(3)和式(4)组成的多智能体系统,采用反步法与改进的动态面结合的方法,给出分布式自适应神经网络控制协议的设计及闭环系统的一致性分析。
2.1 自适应神经网络控制协议设计
首先,定义同步误差zi,1
(9)
其中,aij和bi分别为邻接矩阵A与B中的元素。
对于第m(1≤m≤ni-1) 步,定义误差变量
zi,m+1=xi,m+1-si,m,ei,m=si,m-αi,m
(10)
其中,αi,m是待设计的虚拟控制函数,并将αi,m通过非线性滤波后可得到si,m。 类似于文献[19],非线性滤波器设计为
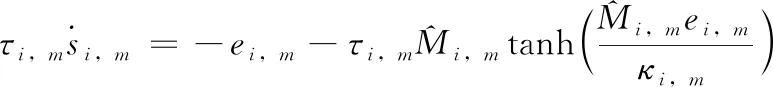
(11)
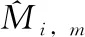
(12)
其中,βi,m和λi,m均为正的调整参数。
步骤1 根据式(9),对其求导,可得
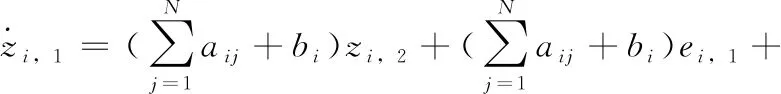
(13)
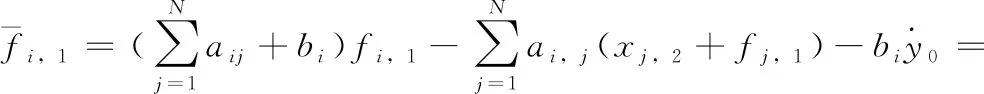
(14)
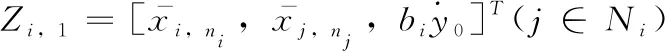
由引理1和引理5可得
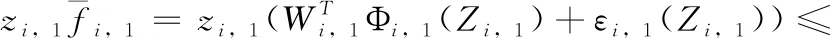
(15)

构造虚拟控制函数αi,1为
(16)
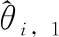
(17)
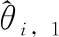
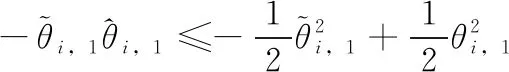

(18)
步骤m(2≤m≤ni-1) 根据式(3)和式(10)~式(11)可得
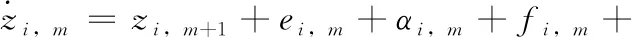
(19)
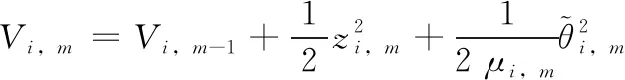
及当3≤m≤ni-1时
(20)
(21)
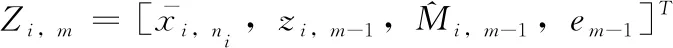
类似于式(15),容易得到
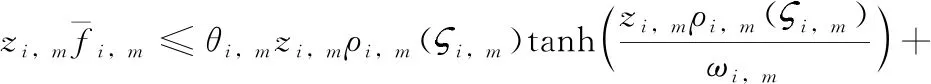
(22)
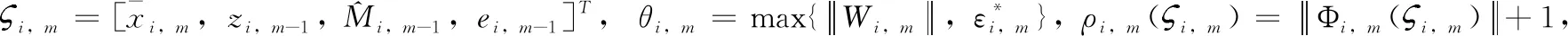
构造虚拟控制函数为
(23)
并选取自适应率为
(24)
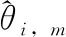
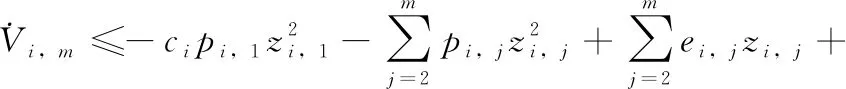
(25)
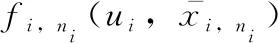
(26)
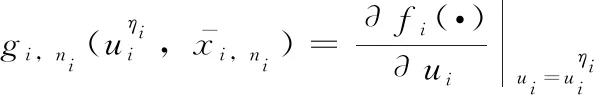
由式(26),关于zi,ni的动态系统可描述为
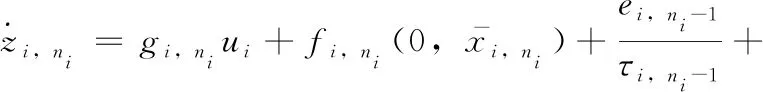
(27)
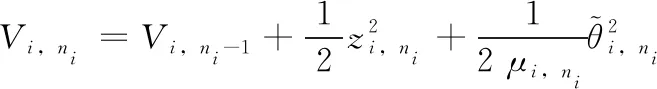
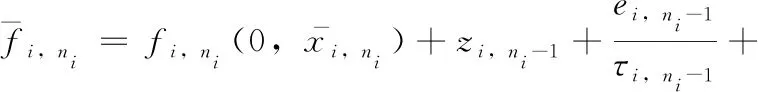
(28)
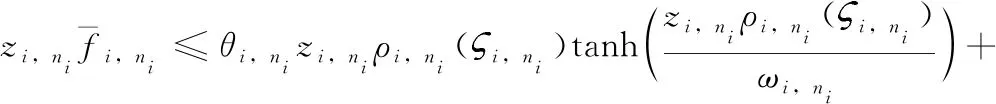
(29)

此时,实际控制协议可设计为
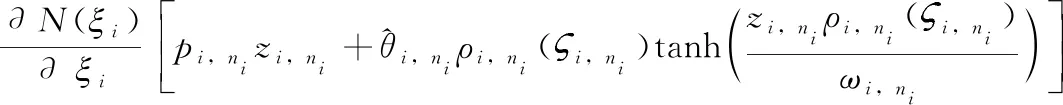
(30)
(31)
(32)
其中,pi,ni和ηi,ni皆为正的设计参数。
则由式(26)~式(32)可得
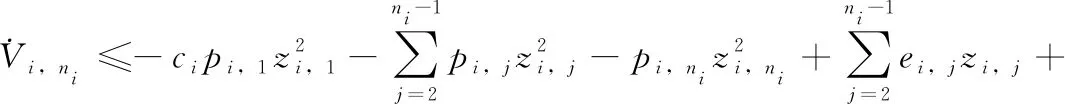
(33)
2.2 一致性分析
根据式(9)~式(11),可得边界层误差ei,m(m=1,2,…,ni-1) 的动态系统为
(34)

则在待定的紧集Ω上,对于m=1,2,…,ni-1, 一定存在正常数Mi,m, 使 |Bi,m|≤Mi,m成立。因此可得如下不等式

(35)
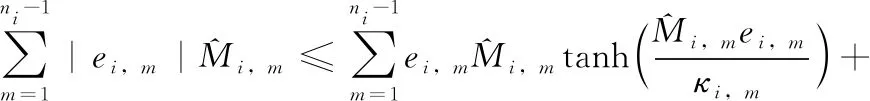
(36)
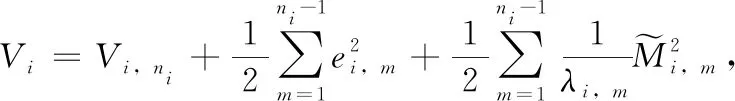
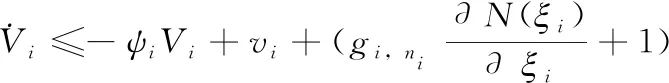
(37)
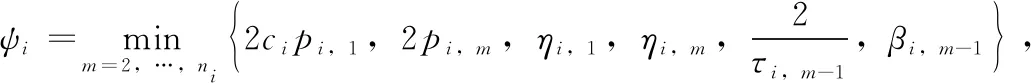
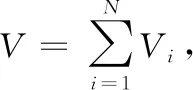
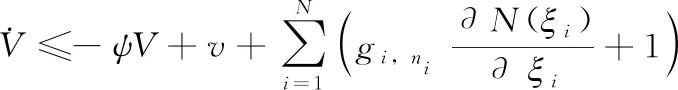
(38)
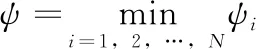
由式(38),并采用文献[26]中类似的方法可得
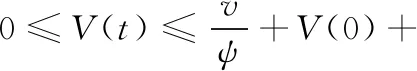
(39)
根据引理4及式(39)可知,V(t) 有界,即存在正常数P0,使得V(t)≤P0, ∀t≥0。 并根据V(t) 的定义可得
(40)
由引理3和式(40)可得,跟踪误差满足不等式
(41)
根据式(39)~式(41)可知,跟随者(3)和领导者(4)之间的所有跟踪误差为合作半全局一致最终有界,且可通过选择合适的设计参数使跟踪误差保持在零点的小邻域内。
基于以上的设计与分析,通过下面定理给出本文的主要结论。

注2:由式(39)~式(41)可以看出,跟踪误差的界在很大程度上取决于常数ψ和v的值的大小。为了获得较小的跟踪误差,可以通过选择合适的设计参数pi,m,ηi,m,μi,m,τi,m,βi,m,λi,m,ωi,m和κi,m使得ψ的值变大且v的值变小。
3 仿真例子
本节通过两个仿真例子说明所提出控制方案的有效性及适用性。
例1:考虑由3个跟随者和1个领导者组成的单杆机械臂系统[18]。图1描述了各智能体之间的信息传递。选取领导者的动态方程为
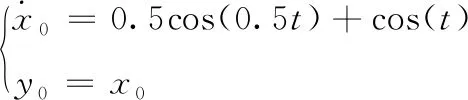
(42)
跟随者的动态方程可描述为
(43)
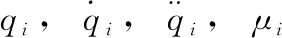
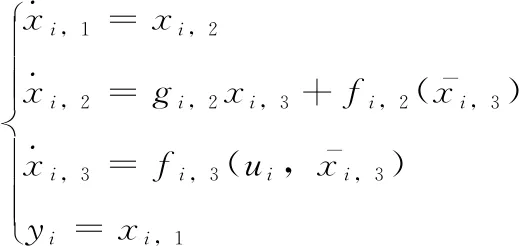
(44)
例1中各智能体之间的信息传递如图1所示。
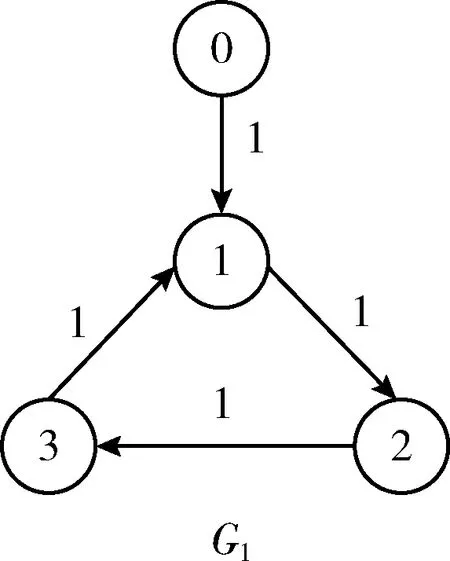
图1 例1中跟随者与领导者之间信息传递拓扑
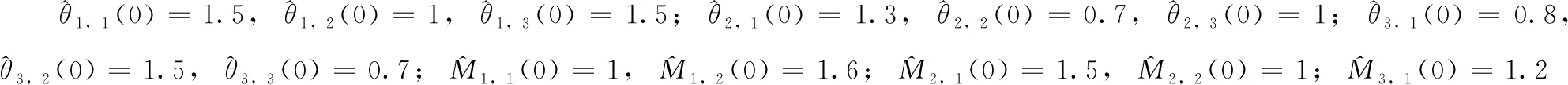
在仿真过程中,设计参数可取为η1,1=17,μ1,1=0.01,ω1,1=0.5,p1,1=10,τ1,1=0.035,κ1,1=0.04,β1,1=0.01,λ1,1=74;η1,2=13,μ1,2=0.02,ω1,2=0.05,p1,2=25,τ1,2=0.01,κ1,2=0.04,β1,2=0.01,λ1,2=68,η1,3=16,μ1,3=0.7,ω1,3=0.07,p1,3=20;η2,1=17,μ2,1=0.6,ω2,1=0.7,p2,1=15,τ2,1=0.035,κ2,1=0.04,β2,1=0.01,λ2,1=75;η2,2=15,μ2,2=0.7,ω2,2=0.05,p2,2=25,τ2,2=0.01,κ2,2=0.04,β2,2=0.01,λ2,2=68,η2,3=16,μ2,3=0.5,ω2,3=0.07,p2,3=20;η3,1=15,μ3,1=0.6,ω3,1=0.05,p3,1=16,τ3,1=0.035,κ3,1=0.04,β3,1=0.01,λ3,1=75;η3,2=20,μ3,2=0.8,ω3,2=0.05,p3,2=10,τ3,2=0.01,κ3,2=0.04,β3,2=0.01,λ3,2=70,η3,3=16,μ3,3=0.7,ω3,3=0.5和p3,3=20。
根据系统(42)~系统(44)和上述参数来设计仿真,其结果如图2~图4所示。
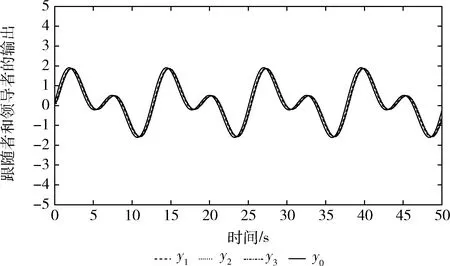
图2 例1中跟随者输出yi(i=1,2,3) 与领导者输出y0
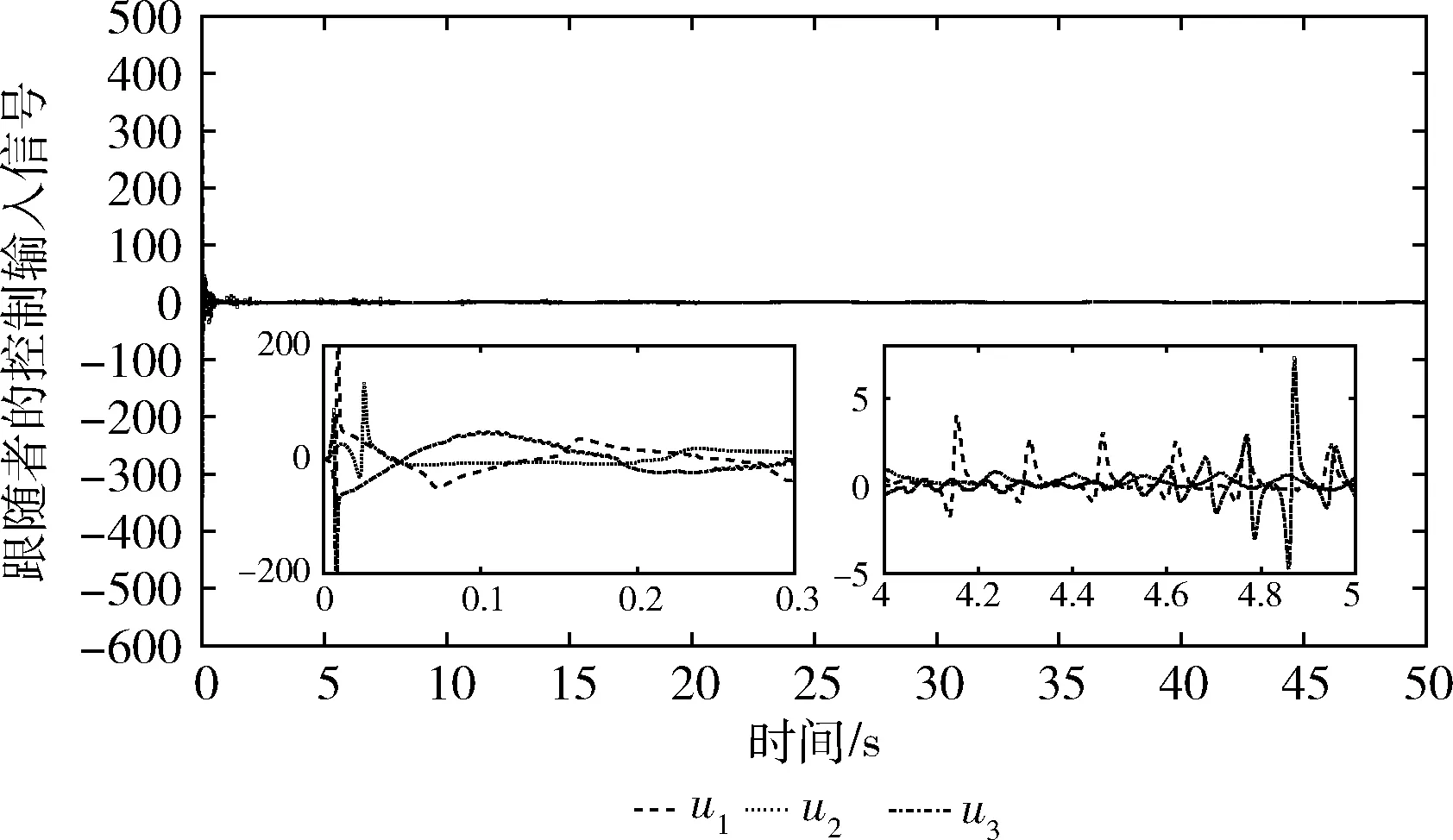
图3 例1中跟随者的控制输入ui(i=1,2,3)
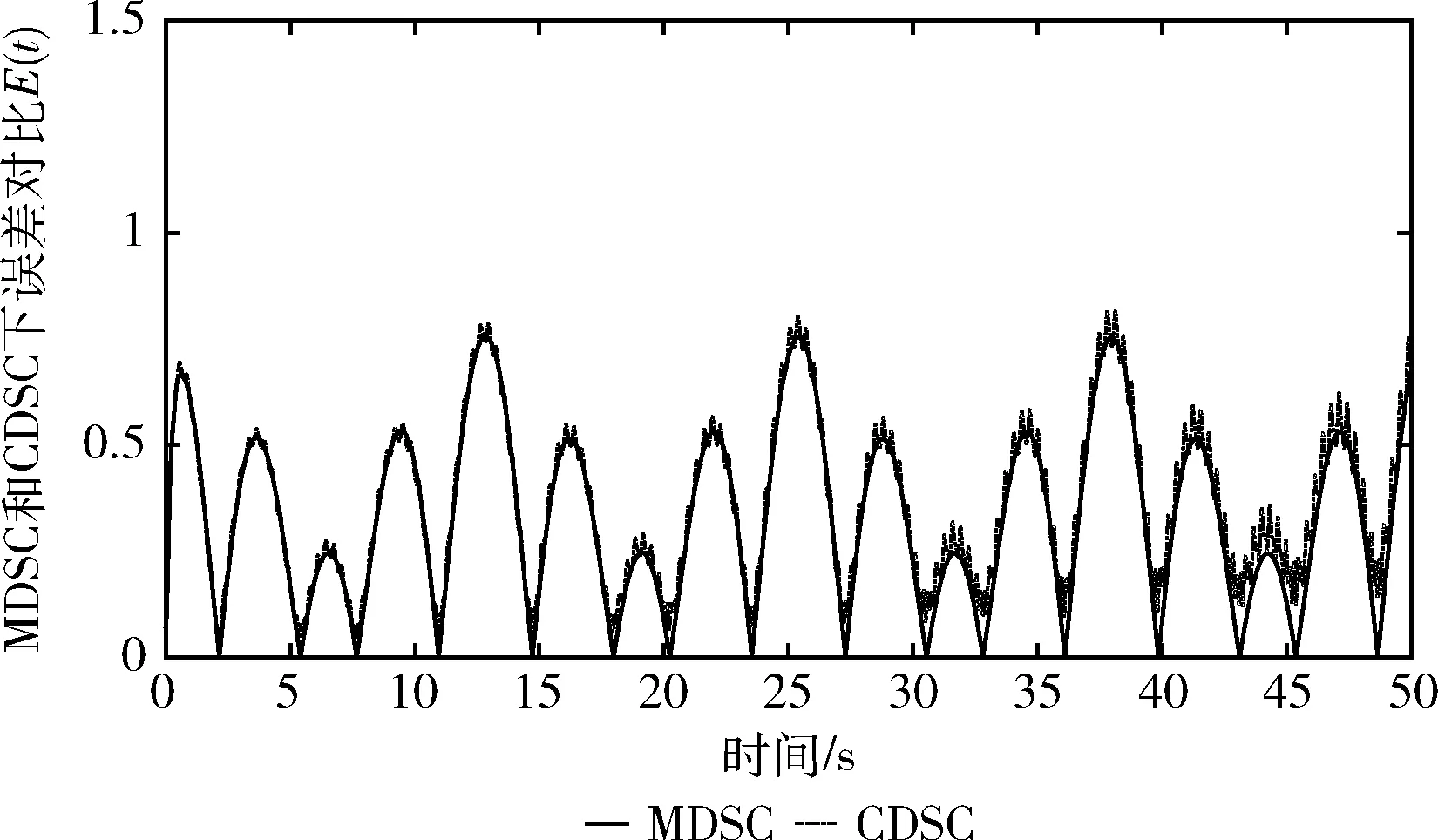
图4 例1中改进动态面控制(MDSC)与传统动态面控制(CDSC)的跟踪误差E(t)
根据图2可看出,所设计的控制策略可以使3个跟随者较好地跟踪领导者的输出,即跟随者的输出曲线能够较好地跟踪领导者的输出曲线的变化而变化,且根据图像可看出,其跟踪误差可以维持在较小的范围内。图3则为各个跟随者的控制输入信号的曲线图。
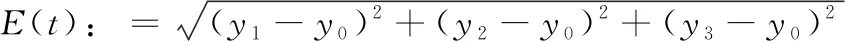
例1中跟随者输出yi(i=1,2,3) 与领导者输出y0的同步性能如图2所示。
例1中各跟随者的控制输入信号ui(i=1,2,3) 如图3所示。
例1中改进动态面控制法(MDSC)与传统动态面控制法(CDSC)的一致性跟踪误差的对比如图4所示。
例2:考虑一个具有3个跟随者 (i=1,2,3) 和1个领导者(标为0)的非线性多智能体系统,其中,第1,2个跟随者为二阶非线性系统,其动态方程为
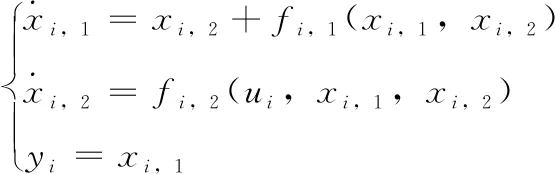
(45)
第3个跟随者为三阶非线性系统,其动态方程为

(46)
领导者的动态方程为
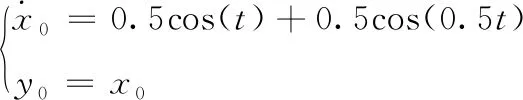
(47)
例2中各智能体之间信息传递如图5所示。
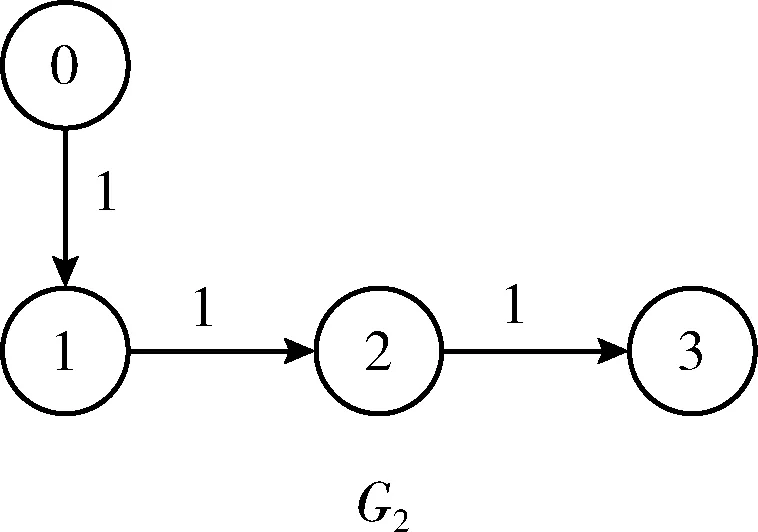
图5 例2中跟随者与领导者之间信息传递拓扑
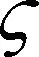
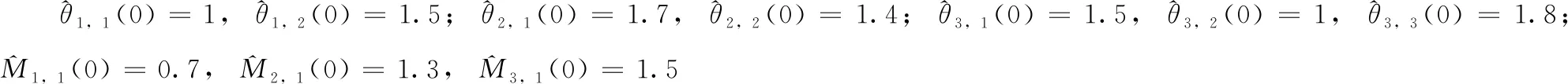
设计参数选取为η1,1=17,μ1,1=0.03,ω1,1=0.1,p1,1=10,τ1,1=0.01,κ1,1=0.04,β1,1=0.01,λ1,1=70;η1,2=1.3,μ1,2=0.02,ω1,2=0.07,p1,2=5;η2,1=15,μ2,1=0.2,ω2,1=0.5,p2,1=8,τ2,1=0.01,κ2,1=0.04,β2,1=0.01,λ2,1=75;η2,2=15,μ2,2=0.01,ω2,2=0.05,p2,2=15;η3,1=30,μ3,1=0.6,ω3,1=0.05,p3,1=16,τ3,1=0.01,κ3,1=0.04,β3,1=0.01,λ3,1=60;η3,2=1.6,μ3,2=0.8,ω3,2=0.5,p3,2=12,τ3,2=0.01,κ3,2=0.04,β3,2=0.01,λ3,2=68,η3,3=16,μ3,3=0.7,ω3,3=0.3和p3,3=5。
仿真结果如图6~图7所示。通过图6可以看出,所提出的控制策略可以使跟随者较好地跟踪领导者的输出。
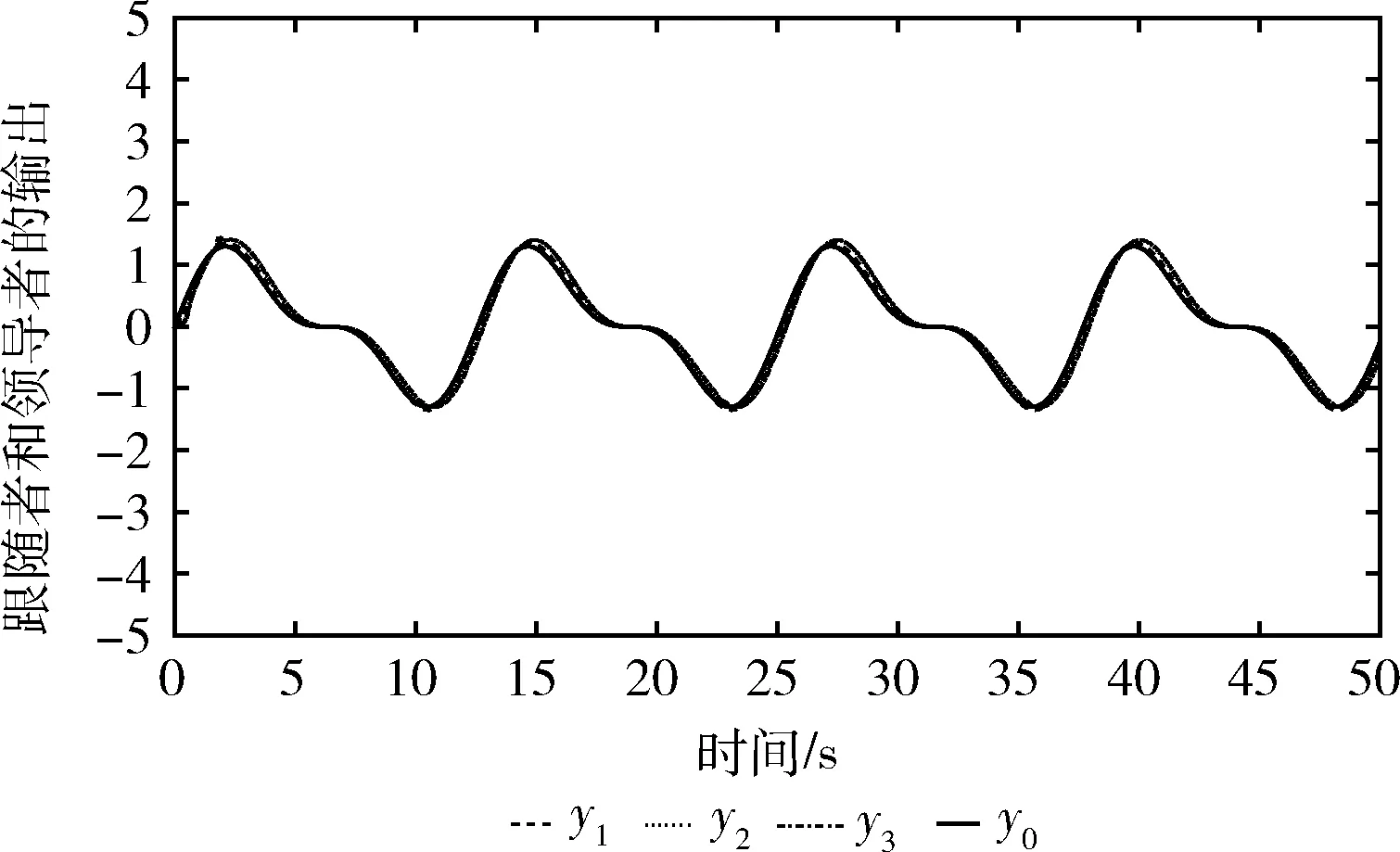
图6 例2中跟随者输出yi(i=1,2,3) 与领导者输出y0
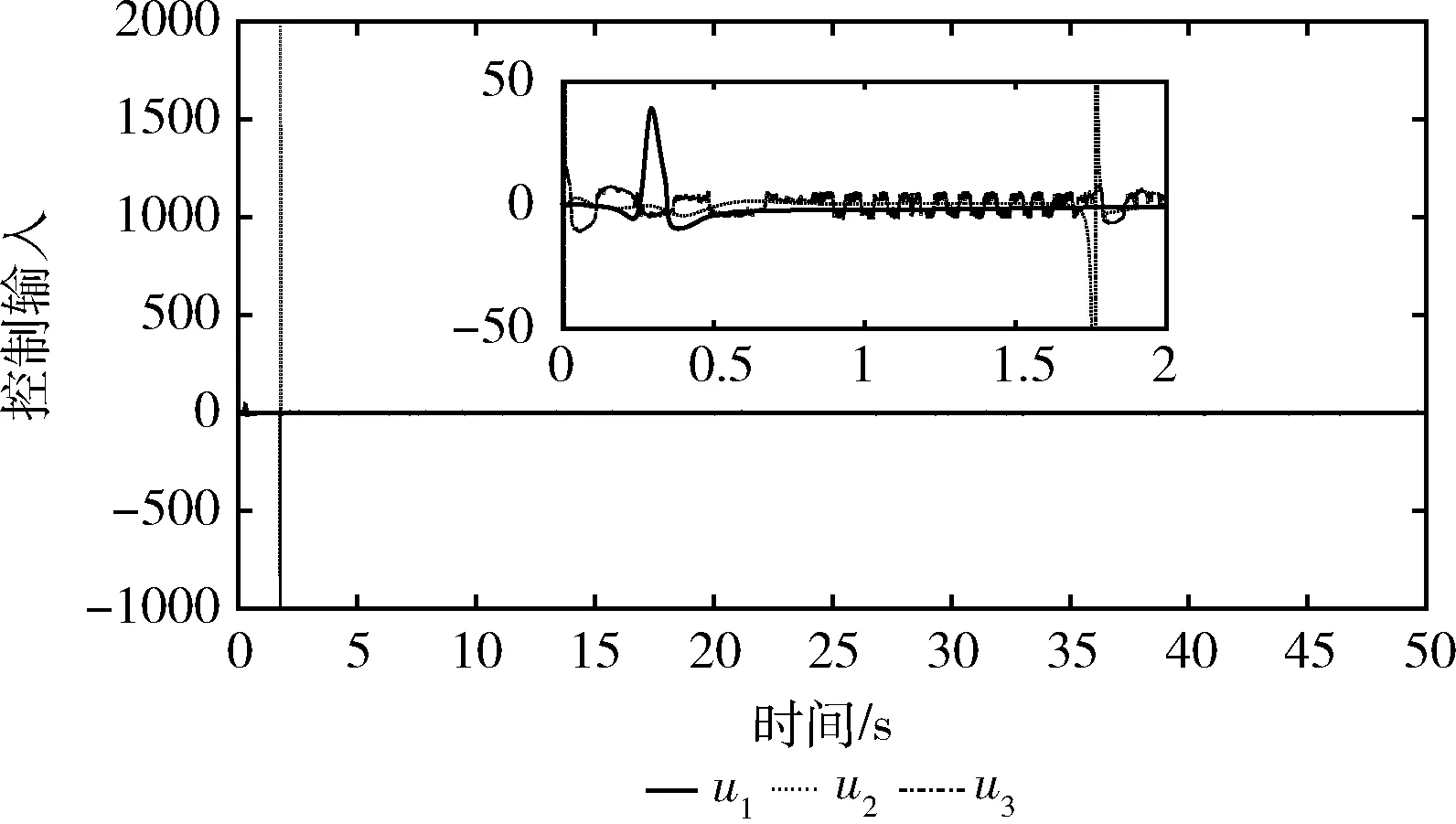
图7 例2中跟随者的控制输入ui(i=1,2,3)
例2中跟随者输出yi(i=1,2,3) 与领导者输出y0的同步性能如图6所示。
例2中各跟随者的控制输入信号ui(i=1,2,3) 由图7所示。
注3:由于系统(44)~系统(46)中考虑了非仿射及非下三角的系统结构和未知控制方向的影响,使得已有的一些控制策略[16-18,24,26]并不适用于这些系统。然而以上仿真结果表明,本文所提出的分布式自适应神经网络控制协议能取得较好的输出同步性能。
4 结束语
本文考虑了有向拓扑图下具有未知控制方向的非仿射多智能体系统的输出一致性问题。在设计控制策略的过程中,针对未知控制方向,引入了Nussbaum函数进行处理,而RBF神经网络及其性质用于处理非下三角形式的系统函数的不确定项及耦合项。同时,提出一种改进的动态面控制法用于自适应神经网络控制协议的设计,以改善传统动态面控制方法的性能。一致性分析和仿真实例都表明了所提出的控制协议有效,即跟随者能够较好地跟踪领导者的输出曲线。下一步的研究将考虑基于切换拓扑图下非仿射多智能体系统的分布式自适应控制问题。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

