飞行器上层大气层空气动力特性探讨

沈 清, 黄 飞, 程晓丽, 靳旭红,2

(1. 中国航天空气动力技术研究院, 北京 100074；(2. 清华大学航天航空学院, 北京 100084)

引 言

我们把飞行器的飞行空域分为4层, 如图1所示, 其中, 20 km以下的地球大气层, 为稠密大气层, 定义为第1空域. 这是航空飞行器所利用的空域. 20～100 km高空为较为稀薄的大气层, 称为临近空间[1], 定义其为第2空域. 这是高超声速飞行器所利用的空域. 300 km以上为外太空, 定义其为第3空域. 这是航天飞行器运用的空域. 100 km为Karman线, 是国际上公认的空天分界线. 100～300 km 区间的上层大气层[2]称为第4空域. 该空域大气密度极低, 高超声速飞行器无法利用其气动力进行飞行, 而航天飞行器又会因为在此处存在气动阻力难以长期在轨飞行. 能否利用该空域的气动力将是本文探讨的主题.

图1 飞行空域的划分与飞行器的应用Fig. 1 Space partition and application of flying vehicles

第4空域属于临近空间向外太空过渡的空域, 存在非常稀薄的大气. 人们希望航天飞行器能够在这一空域进行飞行, 例如, 美国“锁眼(KH-12)”卫星[3-4], 为提高对地观测能力, 在该空域进行轨道的下探和机动变轨, 其最低可下降至120 km. X-37B轨道飞行器也设计成可在该空域利用空气气动的作用进行机动变轨[5-6]. 但是, 由于在上层大气层存在气动阻力, 在该轨道无法维持长期运行, 当完成任务时还须返回原有轨道. 为了解决在这一空域长期飞行的问题, 人们提出了采用高效率的电推进技术克服气动阻力[7-9]. 由此可见, 虽然实现了低轨卫星在该层空域的短时飞行, 但是在这一空域进行长期在轨飞行仍存在很大困难.

人们很早就针对再入返回舱和航天飞机开展了这一空域空气动力学的研究, 若干代表性的工作见文献[10-15]. 为研究卫星的气动阻力特性, 专门开展了卫星的自由分子流研究, 代表性的工作见文献[16-18]. 在这些研究中, 人们认识到飞行器在这一空域遇到的气动力主要成分是摩阻, 造成气动阻力占比超过了50%、 升阻比小于1, 使得人们无法利用这一空域的气动力维持在轨飞行.

能否找到新的途径, 设计出升阻比大于1的气动布局, 使得利用上层大气层长期在轨飞行可行, 是本文关心的问题. 为此, 本文拟选取几类典型航天飞行器外形, 分析它们在该空域飞行的气动特性, 探讨提高升阻比的技术方向.

1 计算方法及气动力分析方法

1.1 方法介绍

空气动力学对于过渡流和自由分子流, 发展了分子运动论和多种模拟方法[19-20]. 对于上层大气层流动, 我们采用了两种方法分析气动力. 一是DSMC方法[19]. 二是自由分子流理论方法[17]. DSMC方法的主要思想是采用有限个模拟分子代替真实分子, 在计算机中进行分子与分子之间、 分子与物面之间的相互碰撞模拟, 整个模拟中分子之间及其与物面之间不断交换动能与内能, 待模拟足够的时间步以后, 采样统计给出每个网格中的宏观流场结果. 计算中分子之间采用VHS碰撞模型, 能量交换采用L-B模型[21], 按照Bird发展的能量按自由度分配原则采用取舍法进行抽样分配, 物面边界条件可根据需要采用完全漫反射条件或一定物面适应系数的Maxwell边界条件, 计算方法的验证见文献[11], 计算结果与Apollo返回器的气动力飞行数据吻合很好. 此外还针对250 km高度对方法进行了验证, 见文献[22], 计算的GOCE卫星气动力结果与文献计算结果吻合较好.

此处, 相对于传统的自由分子流计算模拟, 上层大气层空气动力学须重点考虑气体分子与不同物体表面相互作用的效应. 在本文的研究中, 采用不同的物面适应系数来反映这一特性.

1.2 单位升力面气动载荷特性

高空飞行环境下气动载荷特性与飞行器气动受力面密切相关, 为了简化, 对1 m2的平板气动力特性进行了分析. 假设飞行速度为轨道速度8 km/s, 攻角分别为20°及30°, 轨道高度分别取100， 110， 120， 150， 180， 200， 300 km等典型值, 壁温取为300 K. 此处暂取常规材料的表面适应系数0.85进行分析.

图2～4为气动力计算结果. 图2为攻角20°和30°时产生的横向气动力(垂直于运动方向)随高度的变化. 该结果表明, 随着高度的增加, 气动升力呈指数级下降; 攻角30°时, 当轨道高度从100 km增加至200 km时, 气动升力约从4.5 N降低至约1 mN, 高度进一步升至300 km时, 气动升力降低至约0.05 mN.

图3为攻角20°和30°时气动阻力随轨道高度的变化. 气动阻力规律与气动升力类似. 攻角30°时, 当轨道高度从100 km升至200 km时, 气动阻力约从11 N降低至约5.5 mN, 当轨道高度进一步升至300 km时, 气动阻力降低至约0.25 mN.

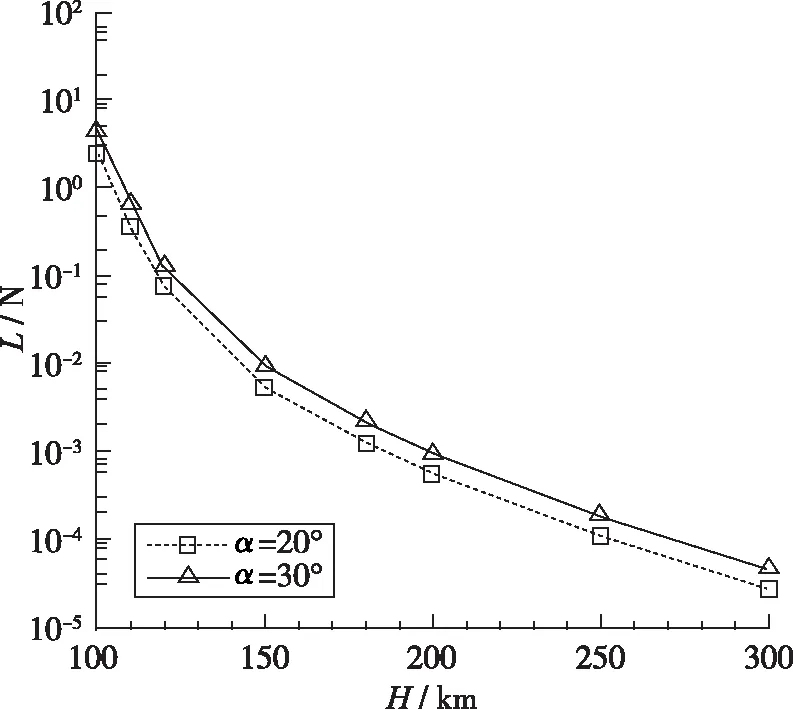
图2 不同攻角下升力特性随高度的变化Fig. 2 Variations of L with altitude

图3 不同攻角下阻力特性随高度的变化Fig. 3 Variations of D with altitude

图4为升阻比随轨道高度的变化特性. 该结果显示出升阻比随轨道高度的增加迅速降低, 在高度150 km以上, 升阻比基本不再随高度升高而下降. 攻角为30°时, 当轨道高度从100 km升至150 km时, 升阻比约从0.4降低至约0.1, 高度进一步升至300 km时, 升阻比降低至约0.18. 我们发现升阻比在所研究的工况下均是小于1的. 这一研究结果表明, 获取气动升力的同时会产生气动阻力, 会消耗轨道能量. 我们认为, 若飞行器升阻比大于1, 即消耗1个单位的轨道阻力可产生大于1个单位的气动升力, 此时采用气动升力进行变轨是有效益的. 当升阻比小于1时, 气动效率低, 气动变轨方式在工程上不具有技术效益.

图4 不同攻角下升阻比特性随高度的变化Fig. 4 Variations of L/D with altitude

图5给出了不同攻角下摩阻占比随轨道高度的变化. 可以发现, 随着飞行轨道高度的提升, 摩阻占比逐渐增大, 在100～150 km之间, 该占比快速增加, 在150 km之后该占比基本不再随高度升高而增加. 随攻角的降低, 摩阻占比迅速增大. 在150 km时, 攻角从45°变化至10°时, 摩阻占比从41%迅速增大至91%. 这个效应导致了飞行器升阻比随轨道高度升高而快速降低.

图5 不同攻角下摩阻占比随高度的变化Fig. 5 Variations of CDf/CD with altitude

2 航天飞行器上层大气层气动特性

本节对航天飞行器的上层大气层气动特性进行了分析, 包括卫星、 再入返回舱、 锥形体和高超声速飞行器等典型外形的上层大气层气动特性. 假设飞行速度为8 km/s, 分别计算了100～200 km高度时的气动特性. 计算中, 表面适应系数按照一般材料选取, 为0.85; 壁温取为300 K.

2.1 立方形卫星

卫星气动特性的分析采用边长为1 m的正方体为例. 几何外形如图6所示. 图7为阻力及升阻比随高度的变化, 可以看出, 该外形阻力值受攻角影响较小, 受轨道高度的影响很大. 其气动阻力随轨道高度的增加呈指数级减小, 升阻比在100～120 km 高度之间变化较为剧烈, 而高度大于120 km 时, 升阻比随高度变化较小. 其中, 在攻角10°时, 高度从100 km升至200 km时, 阻力值约从40 N降低至16 mN, 升阻比约从0.06降低至0.03; 而攻角30°时, 阻力值约从40 N降低至17 mN, 升阻比约从0.07降低至0.03; 从图中还可发现, 攻角约在20°时升阻比大于10°, 30°攻角下的结果, 当高度从100 km升至200 km时, 其值约从0.08降低至0.04. 一般来说, 卫星的外形设计是不考虑气动力效应的, 此类外形的气动力主要体现为阻力.

图6 立方体卫星几何外形Fig. 6 Schematic geometry of a cubic satellite

(a) Drag at different altitudes

2.2 Apollo飞船返回舱

飞船返回舱气动特性的分析采用Apollo外形为例. 几何外形如图8所示. 外形尺寸见文献[10-12]. 图9给出了该外形的气动阻力和升阻比随高度的变化. 可以看出, 该返回舱外形气动特性规律与卫星外形规律相似, 即阻力值随高度的增加呈指数级降低, 且对攻角不敏感, 而升阻比在飞行高度100～120 km之间时变化很大, 大于120 km时随高度变化较为缓慢. 该外形在攻角10°时, 高度从100 km 升至200 km 时, 阻力值约从392 N降低至155 mN, 升阻比约从0.07降低至0.04; 而攻角30°时, 阻力值约从320 N降低至132 mN, 升阻比约从0.2降低至0.1.

图8 Apollo飞船返回舱几何外形Fig. 8 Schematic geometry of the Apollo re-entry capsule

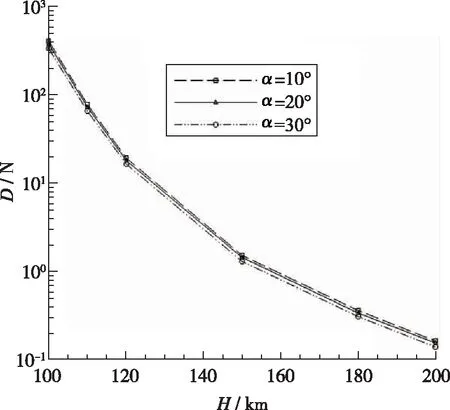
(a) Drag at different altitudes

2.3 圆锥体

锥体飞行器气动特性的分析采用尖锥外形为例. 几何外形如图10所示, 尖锥长4 m, 底部直径2 m. 图11给出了圆锥分别在10°, 20°和30°攻角时的气动阻力和升阻比. 该外形的阻力及升阻比随高度的变化也与前两种外形的气动力变化规律类似, 即阻力和升阻比随高度的增加迅速降低. 从定量结果可以看出, 随着高度从100 km增加至200 km, 攻角在10°和20°时的气动阻力约从60 N 降低至30 mN, 攻角30°时的气动阻力约从80 N降低至40 mN; 攻角10°时的升阻比约从0.16降低至0.06; 攻角在20°和30°时, 升阻比约从0.24降低至0.1.

图10 锥体飞行器几何外形Fig. 10 Schematic geometry of a cone

(a) Drag at different altitudes

2.4 高超声速飞行器外形

对高超声速飞行器外形进行了气动力分析, 飞行器外形取自HTV-2的乘波体几何外形, 如图12所示. 计算中该外形长度取为 4 m, 宽度取为2.2 m.

图12 高超声速乘波体几何外形Fig. 12 Schematic geometry of a hypersonic wave-rider

图13为该飞行器气动力随轨道高度的变化. 与前两种外形气动特性规律不同, 该外形的气动阻力对攻角敏感. 其气动阻力及升阻比随高度的变化与其他外形显示出类似的规律, 即阻力随轨道高度升高迅速降低, 升阻比在轨道高度100～120 km时随高度升高迅速下降, 当轨道高度大于120 km 时随高度变化较为缓慢. 从定量结果可以看出, 小攻角10°时, 高度从100 km增加至200 km时, 阻力则约从27 N降低至14.7 mN, 升阻比约从0.32降低至0.14; 攻角在30°时, 高度从100 km增加至200 km时, 阻力则约从73.5 N降低至34.8 mN, 升阻比约从0.39降低至0.18. 同样还可发现, 该外形在攻角30°时升阻比均大于10°, 20°攻角时的结果.

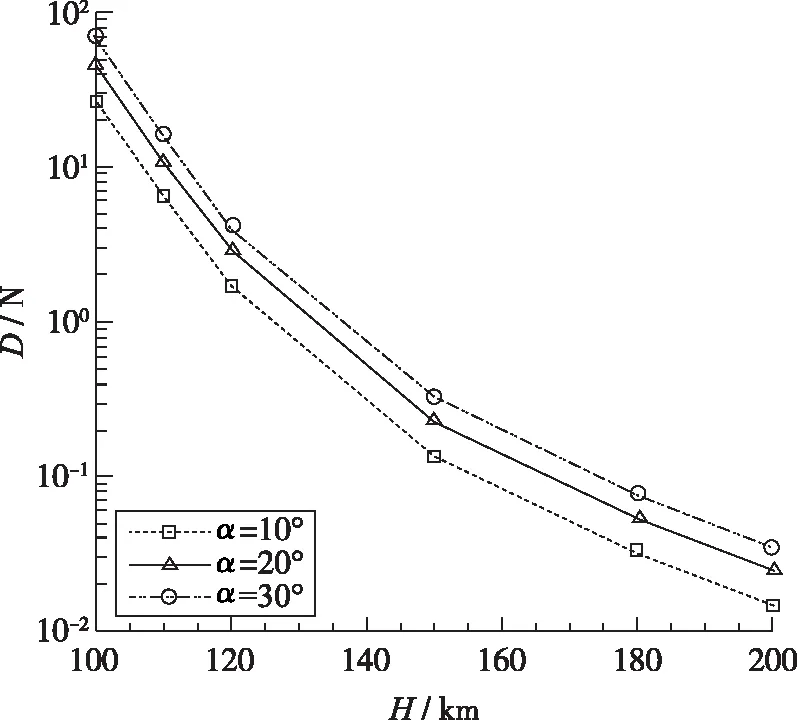
(a) Drag at different altitudes

这些结果表明, 在上层大气层中乘波体的升阻比也是很低的, 在100 km处, 其升阻比接近0.4, 且随着飞行高度的增加持续降低, 这说明上层大气层不适合现有飞行器飞行. 在100 km高度, 乘波体的气动阻力为10 N量级, 在200 km高度, 阻力为100 mN 量级, 这对于航天飞行器是一个很大的阻力, 不利于长期在轨飞行. 如果要发展上层大气层飞行器, 必须采用新的飞行原理, 采用新的技术增升减阻, 才有可能利用上层大气层气动力实现长期在轨飞行.

3 不同表面适应系数对气动力影响的分析

为了探讨不同材料对气动特性的影响, 此处采用不同的表面适应系数进行了气动力计算, 飞行器外形为平板.

表1给出了不同典型材料表面的适应系数值. 表面适应系数反映了材料的表面特性, 其量值取决于表面材料和壁面粗糙度. 一般来说, 对于普通材料, 表面适应系数在0.5～1.0之间. 根据Porodnov等[23]的自由分子流实验, 玻璃的物面系数在0.78～0.89, 反映了普通材料与自由分子流相互作用的情况. 物面系数低, 表明材料的表面光滑.

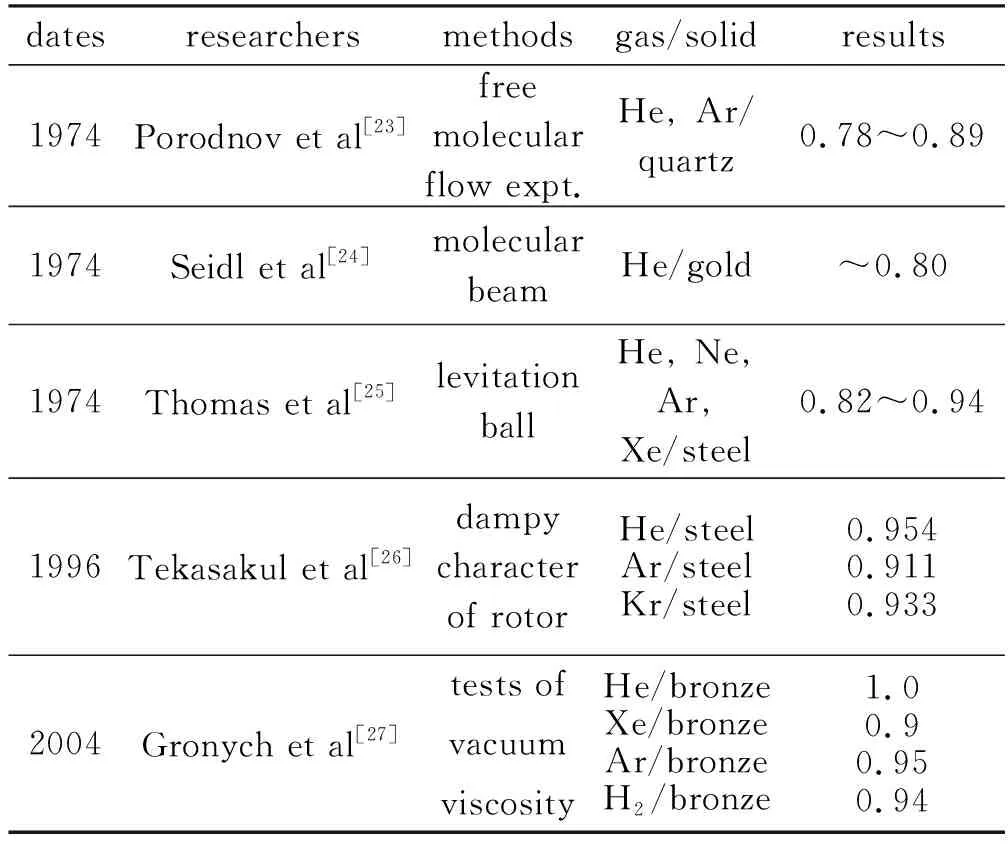
表1 不同典型材料表面的适应系数Table 1 Accommodation coefficients on the surface of different materials

图14, 15及16分别给出了1 m2面积的平板外形在不同轨道高度、 不同物面系数下升阻比、 升力及阻力随攻角的变化. 在算例计算中, 物面适应系数取了4个值, 分别为0.2, 0.5, 0.85, 1.0. 从计算结果中可以发现, 物面适应系数对升阻比、 升力及阻力有重大影响, 物面适应系数大, 升阻比及升力小; 物面适应系数小, 升阻比及升力大; 物面适应系数取0.2和1.0时, 升阻比及升力相差接近一个量级. 可以从自由分子流与物面相互作用的特性来说明这一现象, 物面适应系数越大, 表示气体分子在物面越接近于漫反射, 这会造成气动摩阻增加.

(a) H=100 km

(a) H=100 km

(a) H=100 km

从该计算结果中, 我们还看到, 轨道高度在100～200 km, 物面适应系数为0.2时, 攻角20°附近的升阻比在各轨道高度下均达到最大值且大于1, 而升力则在攻角50°附近达到最大值. 其余物面适应系数下的升阻比均小于1, 且峰值位置约位于30°攻角附近. 因此在上层大气层要想利用气动力进行机动, 须保证物面适应系数尽可能接近于0.2或小于0.2, 以保证获得大于1的升阻比.

此外, 还可发现, 阻力随物面适应系数的变化在50°攻角附近出现反向, 即攻角在0°～50°时, 物面适应系数增大, 阻力增加, 而攻角在50°～90°时, 物面适应系数增大, 阻力降低.

4 结束语

通过对典型飞行器的上层大气层气动力特性及关键影响因素分析, 获得了以下基本认识:

(1)在上层大气层, 不考虑气动外形的卫星体、 考虑再入减速的返回舱、 低气动阻力的锥体和高升阻比的乘波体均显示出升阻比小于1的共性, 这使得在飞行器利用上层大气层进行飞行存在本质上的困难;

(2)物面适应系数对上层大气层气动特性影响较大, 对平板气动力的分析表明, 选取小的物面适应系数材料, 可有效提高升阻比, 当物面适应系数接近0.2时, 存在升阻比大于1的状态, 这一特点体现了上层大气层气动力学的基本特性;

(3)本文的分析结果表明, 飞行器在100～200 km 高度进行轨道飞行, 1 m2的受力面可产生1 mN～1 N的气动力, 若能够设计出升阻比大于1的气动布局, 则有可能实现利用上层大气层飞行.

基于以上认识, 我们认为有必要在第4空域建立上层大气层空气动力学这一学科方向, 开展面向上层大气层飞行器的空气动力学研究.

致谢感谢中国航天科技集团有限公司科技委李锋研究员对本文的技术策划与指导.