高升阻比模型天平校准安装角误差控制要求

吕治国, 赵荣娟, 黄 军

(中国空气动力研究与发展中心超高速所, 四川绵阳 621000)

引 言

在航空航天器地面模拟的风洞实验中, 主要利用天平测量作用在模型上的气动力[1-3], 针对不同风洞实验设备, 发展了多种形式的气动力测量天平[4-12], 天平测量技术发展的同时, 在世界范围内, 也发展了多种与之相适应的天平校准系统[13-18], 以及多种天平校准的数据处理方法[19-27]. 文献[15,17,22-25]涉及天平校准误差分析的内容, 但天平安装方面引起的误差论述相对较少, 文献[13,18,21]也介绍了天平安装, 但没有涉及天平安装误差影响解决方案. 高超声速飞行器的气动力测量风洞实验, 主要利用压电天平、应力波天平等特种天平在激波风洞等脉冲型风洞上进行[28-33].

由于压电天平具有结构简单, 频响高等特性, 在校准公式的应用上, 通常考虑1阶干扰就可以满足测量要求, 因此CARDC激波风洞发展压电天平作为气动力测量的天平. 在压电天平的单分量校准过程中, 首先将压电天平通过锥套配合的方式固定安装在校准台上, 然后采用快速卸掉砝码载荷的方式实现天平校准, 校准法向力或俯仰力矩以及轴向力通常是将天平法向力正方向向上安装, 如图1所示. 校准法向力时将天平水平安装在校准台架上, 直接在校准加载套上悬挂砝码, 通过改变砝码质量实现法向力变化校准; 校准俯仰力矩是通过在天平校准加载套上悬挂固定质量砝码, 改变砝码悬挂位置, 实现力矩变化校准; 校准轴向力则是采用在天平支杆轴线的延长线方向, 也就是轴向力反方向, 加载线绕过滑轮后悬挂上可以变化的砝码, 实现对天平轴向力校准; 由于校准侧向力和偏航力矩是采用将天平绕旋转轴逆时针(轴向力正方向)旋转90°后水平安装, 所以, 天平校准安装角误差也会对侧向力以及偏航力矩产生与法向力和俯仰力矩相类似的影响.

在直角坐标系下, 会有3个角度误差, 除了水平安装角和滚转安装角外, 还有侧向安装角. (通过坐标系变化, 上述3个安装角分别对应气动力测量模型上的攻角、滚转角和侧滑角, 在不引起误会的前提下, 本文分别简称为攻角、滚转角和侧滑角.) 这3个安装角误差均会给天平校准结果带来误差, 但在天平的单元校准中, 对于直接采用砝码载荷校准来讲, 毫无疑问, 攻角误差和滚转角误差会直接引起天平校准载荷的误差, 在天平采用通过旋转后校准侧向力分量和偏航力矩分量过程中, 天平侧滑角则不会给天平侧向力分量和偏航力矩分量的加载载荷带来误差, 因此也不会给校准结果带来误差, 实际上由于天平的旋转, 攻角误差或滚转角误差代替了侧滑角误差对天平校准加载载荷产生影响, 因此, 本文初步分析攻角误差和滚转角误差对天平校准结果的影响, 进而提出对这两个角度的控制要求.

在天平的校准中, 通常将天平通过尾部承载锥段安装在天平校准台架上, 由于加工或装配的误差, 安装的天平并不是处于绝对水平的状态, 相对于天平体轴系而言, 通常天平安装在校准台上存在一个小的攻角误差和小的滚转角误差, 这两个安装角误差会对压电天平校准产生加载误差, 该加载误差对压电天平各个分量的校准或测量影响差别较大, 有的分量受到的影响相对较小, 可以忽略不计, 有的分量受到的影响相对较大. 那么在有安装角误差情况下, 砝码加载会产生多大的误差呢？这个误差对天平校准影响有多大？什么样的校准安装角误差是可以接受的呢？

从测量环节来看, 针对不同的飞行器模型, 天平校准安装角误差允许的情况显然不同, 对于高升阻比模型[34-37](如乘波体外形)气动力测量, 大载荷分量对小载荷分量的干扰(如法向力对轴向力、法向力对侧向力等)对于这两个安装角度误差的控制要求就会与校准时不一致. 本文从高升阻比模型的大载荷分量对小载荷分量干扰的测量环节对校准安装角度误差控制要求进行研究.

如图1所示, 假定天平安装有攻角误差σα和滚转安装误差σγ(也就是天平体轴系(XT,YT, ZT)与地轴系(X，Y，Z)的两个夹角), 这两个安装角的角度误差可以由多个因素引起, 如天平校准支座加工误差、天平尾端锥与锥孔及键槽连接误差、天平支杆弯曲、校准加载套与天平前端连接误差、加载线角度误差等, 这些误差之间既有叠加, 也有抵消, 在它们共同作用下, 最终效果与天平校准支座加工误差带来的效果一致. 但具体分析这些误差不仅困难, 也相当繁琐. 如天平支杆在校准载荷下弯曲引起的攻角误差, 是非线性的; 校准加载套与天平前端连接以及天平尾端锥与锥孔及键槽连接等误差均会带来攻角误差和滚转角误差. 需要说明的是: 攻角误差σα和侧滑角误差σβ在进行轴向力加载校准的时候, 也会带来砝码载荷误差, 继而也会给天平校准结果带来误差, 在天平校准过程中, 通常采用分别将天平绕其轴线旋转180°两次校准, 通过数据处理可以消除攻角误差和侧滑角度误差引起的砝码载荷误差. 另一方面, 由于在风洞实验中流向角以及攻角机构加工误差等, 导致风洞实验和天平校准的攻角会有差异, 该差异引起的误差与天平校准攻角误差引起的误差类似, 本文为了便于简化分析, 就以天平安装支座加工误差带来的攻角和滚转角两个角度误差为例分析说明.

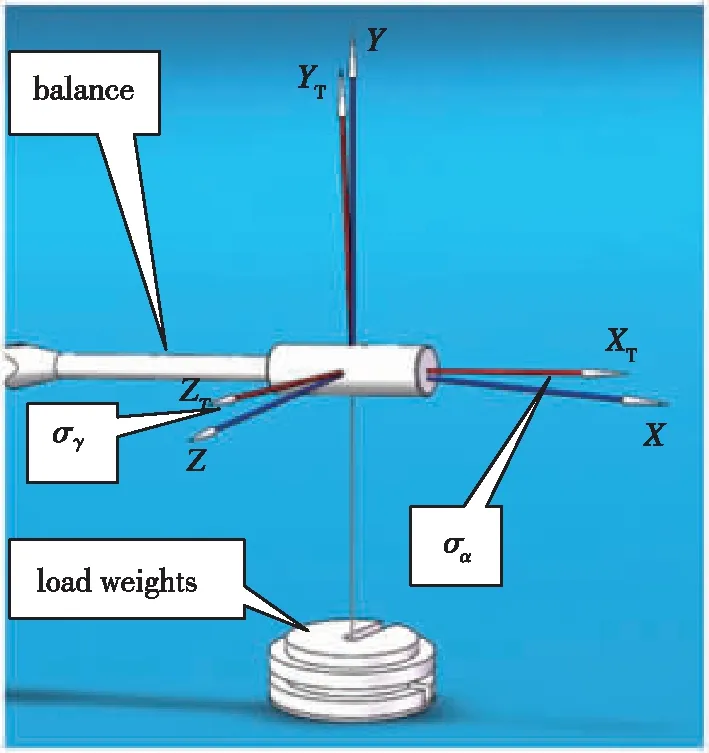
图1 天平校准安装及坐标系简图Fig. 1 Sketch of balance mounting and coordinate system

1 力分量校准对安装角误差控制要求

1.1 力分量校准对攻角误差控制要求

假定校准法向力主分量悬挂的砝码载荷为m1g, 则作用在天平法向力方向上砝码载荷的投影为m1gcosσα, 攻角误差引起的法向力加载相对误差为

(1)

假定σα为10′或30′, 则ΔN/N分别为4.2×10-6或3.8×10-5, 显然, 这样的误差在天平实际测量过程中几乎是可以忽略不计的. 进一步考察式(1), 如果允许ΔN/N≤0.1%, 则σα≤2.556 1°; 如果允许ΔN/N≤0.5%, 则σα≤5.703 2°; 如果允许ΔN/N≤1%, 则σα≤8.089 2°; 因此, 只要攻角小于2.556 1°, ΔN/N≤0.1%.

在轴向力分量校准时, 假定攻角误差也为σα, 导致加载线上作用的载荷m2g在天平体轴系轴向力的投影也为m2gcosσα, 与法向力加载校准类似, 轴向力加载的相对误差也为

(2)

如前所述, 由于压电天平单元校准侧向力是通过将天平绕旋转轴逆时针(轴向力正方向)旋转90°后水平安装, 采用与法向力校准类似的方法悬挂砝码卸载校准, 与法向力加载类似, 不妨假定攻角误差也为σα, 由此误差引起的侧向力加载相对误差为

(3)

与对法向力加载校准影响类似, 只要攻角误差小于2.556 1°(为节省篇幅, 以下记为2.55°), 轴向力和侧向力的加载相对误差均分别小于0.1%, 通常攻角误差应小于10′, 显然, 实际的校准中, 这个由攻角误差导致的主分量加载误差是可以不考虑的.

对轴向力、法向力、侧向力的加载校准而言, 只要攻角度误差小于2.55°, 该角度误差导致的加载相对误差小于0.1%.

1.2 力分量校准对滚转角误差控制要求

对于轴向力校准而言, 由于小的滚转角与轴向力校准载荷存在垂直投影关系, 因此滚转角安装误差对轴向力校准没有直接的影响.

如前所述, 侧向力与法向力加载情况类似, 为节省篇幅, 仅对法向力加载情况进行分析, 如图2所示, 假定砝码载荷为m3g, 则作用在天平法向力方向的砝码载荷为m3gcosσγ, 由于小滚转角引起的法向力加载相对误差为

(4)

由上可见， 式(4)与式(1)和(2)形式上是一致的, 因此, 可以直接得到类似的结果: 只要滚转角度误差小于2.55°, 该角度误差导致的法向力或侧向力加载相对误差小于0.1%.

2 力矩分量校准对安装角误差控制要求

2.1 力矩分量校准对攻角误差控制要求

如前所述, 由于校准侧向力和偏航力矩是将天平绕支杆旋转90°后采用与校准法向力和俯仰力矩类似的方式进行的, 因此, 攻角误差对偏航力矩的影响和对俯仰力矩的影响是类似的. 本文仅分析攻角误差对俯仰力矩的影响.

如图2, 3所示, 有攻角误差时, 除了如前所述砝码质量由m1g变为m1gcosσα外, 还对加载位置也就是力矩校准的力臂产生影响, 假定加载点距力矩参考点距离为x1, 力矩校准悬挂的砝码加载点中心与天平对称轴中心距离为R, 在没有攻角误差时, 产生的俯仰力矩为

Mz=m1gx1

(5)

当有攻角误差时, 俯仰力矩加载的力臂为

x2=(x1+Rtanσα)cosσα

(6)

因此在攻角误差下, 天平校准加载的俯仰力矩为

MZα=m1gcosσα(x1+Rtanσα)cosσα

(7)

图2 无攻角误差下俯仰力矩校准示意图Fig. 2 Depiction of pitching moment calibration without attack angle error

图3 有攻角误差下俯仰力矩校准示意图Fig. 3 Depiction of pitching moment calibration with attack angle error

由攻角误差导致的俯仰力矩加载相对误差为

(8)

化简整理式(8)后, 可以得到

(9)

假设俯仰力矩校准悬挂的砝码加载点中心与天平平直段对称轴线距离为80 mm, 加载砝码悬挂点与力矩中心双边的纵向位置变化范围是5～95 mm, 式(9)计算结果表明: 除了攻角对俯仰力矩校准相对误差有影响外, 加载点中心距离和加载点的纵向位置之比也对其有影响.

进一步考察式(9), 对于力矩中心一边5, 45和95 mm的悬挂砝码纵向位置, 另一边基本上与此对称, 如果允许ΔMZ/MZ≤0.1%, 那么就允许攻角分别为σα≤0.2′，σα≤1.9′，σα≤4.0′; 如果允许ΔMZ/MZ≤0.5%, 那么就允许攻角分别为:σα≤1.0′，σα≤9.0′，σα≤20′; 如果允许ΔMZ/MZ≤1%, 那么就允许攻角分别为σα≤2.1′，σα≤19′，σα≤41′. 对比前面力分量校准对攻角误差的要求, 显然, 俯仰力矩校准对天平攻角误差要求要远高于力分量校准的要求. 此外, 在校准俯仰力矩时, 加载点偏离天平校准中心从而增大力臂, 可以降低对攻角误差控制的要求.

滚转力矩的校准与俯仰力矩或偏航力矩的校准略有不同, 它是在天平水平安装下, 通过悬挂砝码绕天平轴线(图4为天平校准安装前视图)形成滚转力矩进行校准. 因此, 攻角对滚转力矩校准中力值的影响与校准天平力分量的影响一致; 攻角误差对滚转力矩校准力臂没有影响. 因此, 滚转力矩的校准与天平的力分量校准对于攻角误差控制是相同的.

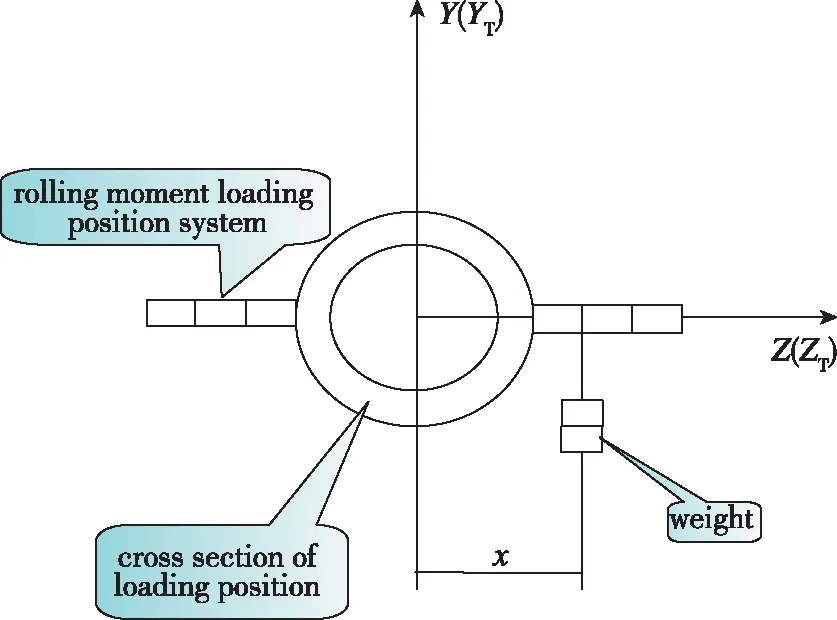
图4 无滚转角误差时加载滚转力矩示意图Fig. 4 Depiction of rolling moment calibration without roll angle error

2.2 力矩分量校准对滚转角误差控制要求

俯仰力矩和偏航力矩可以分解为力和距离的乘积, 所以, 滚转角误差对这两个力矩的影响均可以分为两个部分来考察, 首先是滚转角误差对两个力矩中力的影响, 这个影响前面已经分析过了, 也就是与法向力或侧向力的影响类似. 其次, 滚转角误差对两个力矩中的距离没有直接的影响. 因此, 滚转角误差对两个力矩的影响与法向力和侧向力影响类似, 只要滚转角度误差小于2.55°, 该角度误差导致的俯仰力矩或偏航力矩加载相对误差小于0.1%.

当无滚转角误差时, 如图4所示, 砝码质量为m1g, 加载滚转力矩的力臂长度为x, 则天平滚转力矩为

MX1=KMXm1gx

(10)

当有滚转角误差时, 如图5所示, 砝码质量仍然为m1g, 加载滚转力矩的力臂长度为x1, 而两个力臂长度关系为

x1=xcosσγ

(11)

因此在有滚转角误差情况下, 天平滚转力矩为

MX2=KMXm1gxcosσγ

(12)

由滚转角误差导致的滚转力矩加载校准相对误差为

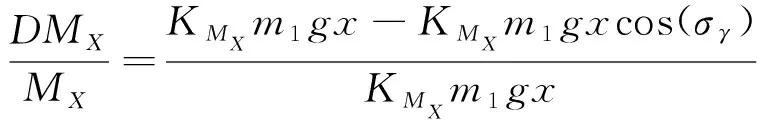
(13)

式(13)与前面式(1)～(3)的攻角误差对力分量的相对误差影响类似, 因此, 可以推论出: 只要滚转角度误差小于2.55°, 该角度误差导致的滚转力矩加载校准相对误差小于0.1%.

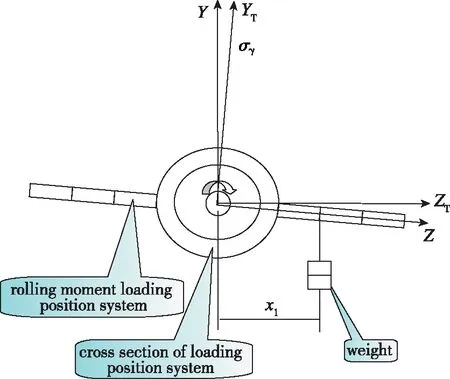
图5 有滚转角误差时加载滚转力矩示意图Fig. 5 Depiction of rolling moment calibration with roll angle error

3 分量间干扰校准对安装角误差控制要求

3.1 攻角误差控制要求

对于高升阻比模型, 由于轴向力加载载荷相对法向力(或俯仰力矩、甚至侧向力和偏航力矩, 以下不再区别提出)较小, 其轴向力对法向力干扰的显著性相对较弱, 扣除了轴向力对法向力天平分量的固有干扰后, 剩下的由攻角误差造成的轴向力对法向力分量间干扰相对较小, 忽略这个干扰不会导致实验数据异常; 相反, 由于法向力加载载荷相对于轴向力较大, 法向力对轴向力干扰较显著, 即使扣除法向力对轴向力固有干扰后, 攻角误差导致的法向力对轴向力干扰依然显著, 忽略这个干扰就会导致实验数据异常. 鉴于此, 为简化分析, 重点考虑法向力对轴向力的干扰对攻角误差控制, 由于攻角误差存在, 加载砝码质量m1gsinσα直接作用在轴向力上, 也就是直接引入伪干扰, 对天平法向力校准来说, 除了法向力主分量加载外, 轴向力上也有个投影分量加载, 因此轴向力输出中除了法向力对轴向力的正常干扰输出外,m1gsinσα分量也产生输出. 当无水平角误差时, 天平法向力对轴向力干扰输出表示为

VNA=KNAm1g+bNA

(14)

当存在水平角误差时, 天平法向力对轴向力干扰输出表示为

VNAα=KNAm1gcosσα+KAAm1gsinσα+bNAα

(15)

对于式(15), 可以改写为

VNAα=(KNAcosσα+KAAsinσα)m1g+bNAα

=KNAαm1g+bNAα

(16)

式(16)是带有水平角误差后砝码质量与天平输出的直线拟合关系式, 天平校准时同样可以采用最小二乘法求出在有水平角下法向力对轴向力干扰输出系数KNAα

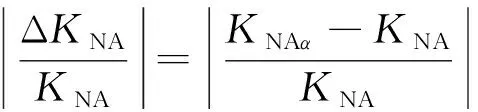
(17)

假定轴向力主系数与法向力对轴向力干扰系数之比的范围为100～400, 式(17)计算结果见表1.

由表1可以看出: 法向力对轴向力干扰系数校准对于天平的攻角要求比主分量和力矩分量校准要求高得多, 以KAA/KNA=100～400为例, 当要求ΔKNA/KNA小于1%时, 要求相应的攻角误差范围为0.34′～0.08′, 达到这个要求相对非常困难, 或者说想要实现这样的误差控制, 须付出非常高昂的代价.

表1 校准攻角允许误差/(′)Table 1 Attack angle tolerance in balance calibration/(′)

3.2 滚转角误差控制要求

为简化分析, 本文主要考虑法向力对侧向力干扰情况, 由于小滚转角存在, 在校准法向力对侧向力干扰时, 砝码载荷在侧向力上有个投影分量, 这个投影分量值为m1gsinσγ, 假定侧向力主系数为KZZ以及法向力对侧向力干扰系数为KNZ, 天平法向力对侧向力干扰输出为VNZ(暂不考虑其他分量对侧向力干扰), 当无滚转角时, 天平法向力对侧向力干扰输出为VNZ为

VNZ=KNZm1g+bNZ1

(18)

当有小滚转角σγ时, 天平法向力对侧向力干扰输出为VNZ为

VNZ=KNZm1gcosσγ+KZZm1gsinσγ+bNZ2

(19)

式(18)和(19)中,bZN1和bZN2均为天平校准输出信号方程的截距, 为小的常数, 改写式(19)

VNZ=(KNZcosσγ+KZZsinσγ)m1g+bNZ2

(20)

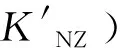
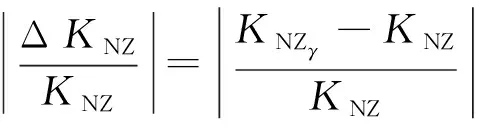
(21)

压电天平侧向力主系数与法向力对侧向力干扰系数比值通常在40～100范围内, 假定KZZ/KNZ=40, 同时仍然假定σγ为10′或30′, 则由式(20)计算出天平法向力对侧向力的干扰系数相对误差, 分别可以达到11.64%和34.91%. 如果KZZ/KNZ=100, 其相对误差分别可以达到29.09%和87.27%. 显然, 具有这样相对误差水平的天平分量间的干扰系数是不可信的, 这对于高精度6分量气动力测量来讲也是不能够接受的.

对于式(21), 可从另一个方面来理解, 以滚转角为变量计算其相对误差, 结果见表2, 可见如果限制KNZ相对误差在0.5%以内, 也就是ΔKNZ/KNZ≤0.005, 同样对于KZZ/KNZ=40, 可以接受的σγ≤0.42′, 对于KZZ/KNZ=100, 可以接受的σγ≤0.17′. 换句话说, 只要滚转角大于0.42′, 法向力对侧向力干扰系数误差在KZZ/KNZ≤40就会大于0.5%; 如果控制这个误差小于0.5%, 通常要求这个滚转角小于0.17′, 这个要求是非常苛刻的.

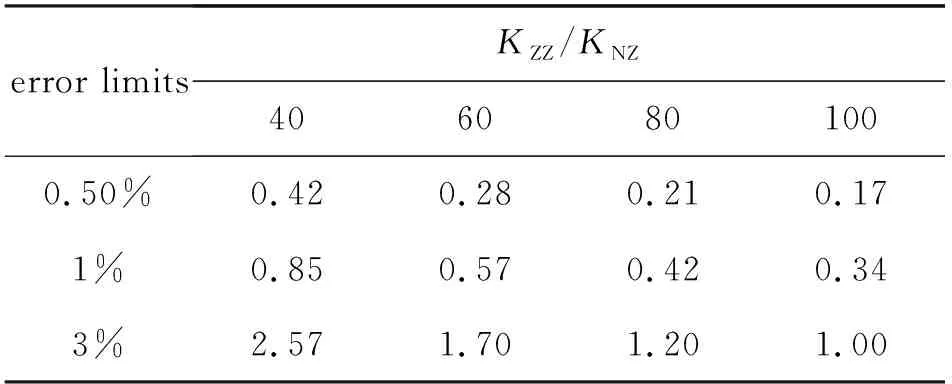
表2 相对误差限下允许滚转角误差限/(′)Table 2 Roll angle tolerance in different relative errors/(′)

3.3 实验测量对攻角误差控制要求

单纯从校准角度考虑, 校准法向力对轴向力干扰系数, 要求的攻角误差控制非常困难, 实现的难度极大, 下面从天平测量输出大小入手, 考察天平校准攻角误差控制问题, 天平校准和测量时, 为了简化, 仅考虑法向力对轴向力测量的干扰项, 天平校准安装无水平角误差时, 风洞实验天平测量时轴向力的输出为

VAA=KAAA+KNAN+bAA

(22)

天平校准安装有水平角误差, 风洞实验天平测量时轴向力的输出为

VAAα=KAAAcosσα+(KNAcosσα+KAAsinσα)N+bAAα

(23)

为了简化, 略去截距项, 风洞实验时天平轴向力的输出相对误差可以表示为

(24)

对式(24)简化, 将第3项分子和分母同时除以流场动压和参考面积, 即将轴向力和法向力值分别以相应的系数表示, 即得到式(25), 再将YDTP-1301天平的一次KAA和KNA校准结果, 即KAA=582.584,KNA=4.110代入, 同时以激波风洞某高升阻比模型天平测量结果的法向力系数和轴向力系数之比(5～25)范围内的结果代入式(25)得到式(26)

(25)

(26)

轴向力风洞测量输出相对误差式(26)的计算结果见表3, 当要求相对误差ΔVAA/VAA低于1%时, 如果风洞实验测量中法向力系数与轴向力系数之比范围为5～25, 天平校准时攻角允许误差范围分别是7′～1.6′, 对比前面的干扰系数校准分析, 这个攻角误差控制要求比校准要求降低一些, 在校准过程中经过细致调整是可以达到的.

表3 测量环节推出校准攻角允许误差/(′)Table 3 Attack angle tolerance in measurement/(′)

3.4 实验测量对滚转角误差控制要求

假设天平在风洞实验测量时无攻角误差, 但天平与模型安装有一个顺时针方向的σγ误差, 也就是模型体轴系与气流轴系或天平轴系就有一个小的滚转角σγ, 如图6所示, 据此分析, 假定模型的准确的气动力为: 体轴系的法向力为Y, 侧向力为Z, 由于存在小的滚转角安装误差σγ, 导致天平测量出的法向力为

Y1=Ycosσγ-Zsinσγ

(27)

同理, 天平测量出的侧向力为

Z1=Ysinσγ+Zcosσγ

(28)

比较天平测量没有滚转角误差和有滚转角误差形成的相对误差如下

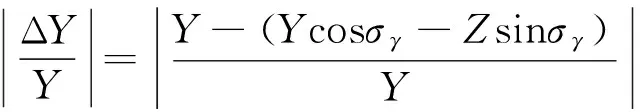
(29)

同理, 对于侧向力的测量, 其相对误差如式(30)所示, 由该式可以看出, 侧向力测量的相对误差与法向力和侧向力的比值相关性非常大, 而法向力和侧向力比值的大小随不同外形, 不同的攻角以及不同的侧滑角均不相同, 相同的误差限在不同法向力与侧向力比值对应允许的滚转角度是不相同的. 按某升力体外形在一次实验测量结果来看, 其法向力与侧向力的比值范围大体上在10～100之间.

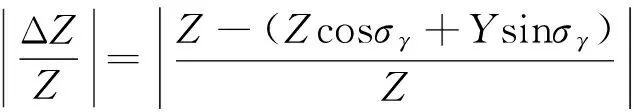
(30)

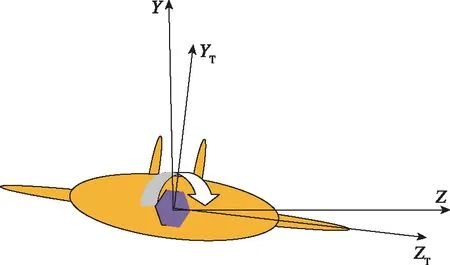
图6 滚转角误差影响测量示意图Fig. 6 Sketch of the influence of roll angle error on the measurement

表4为法向力测量相对误差对滚转角允差, 表5为侧向力测量相对误差对滚转角允差, 对于法向力测量来讲, 从表4和表5对比可以看出: 如果限定0.5%的相对误差, 当法向力和侧向力比值分别取20, 40, 60, 80, 100时, 法向力测量允许滚转角偏差分别为3.50°, 4.33°, 4.67°, 5.00°, 5.00°; 侧向力测量相应的滚转角偏差分别为0.8′, 0.4′, 0.2′, 0.1′, 0.1′. 同样, 当限定1%的相对误差, 法向力测量允许滚转角偏差分别为5.67°, 6.67°, 7.17°, 7.33°, 7.50°; 侧向力测量允许滚转角偏差为1.5′, 0.8′, 0.5′, 0.4′, 0.3′. 从上述对比可以看出: 相对法向力的测量, 侧向力的测量对于滚转角允许的偏差小得多, 对于校准和试验测量环节, 这样的滚转角误差控制要求是异常苛刻的, 准确测量以及安装调整这个滚转角非常困难. 常规的角度测量精度为1 mrad(0.0573°)[38]是不能够满足测量要求的, 只有配置测量精度达到或超过0.001°的角度测量系统[39-40], 才能将天平滚转角调整到小于0.1′的水平, 满足高升阻比模型侧向力测量要求.

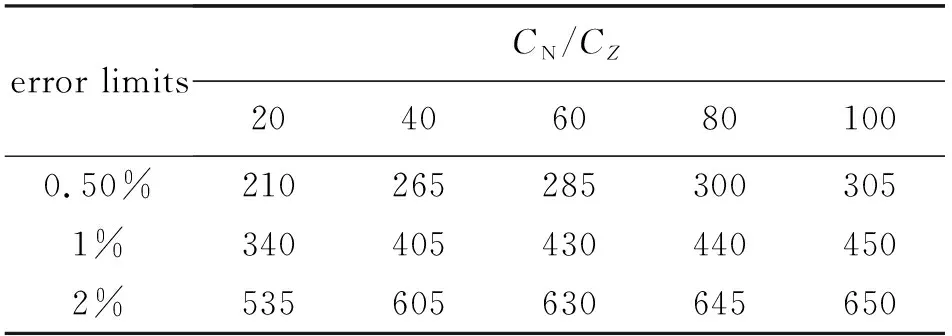
表4 法向力测量相对误差对滚转角允差/(′)Table 4 Roll angle tolerance in normal force measurement/(′)

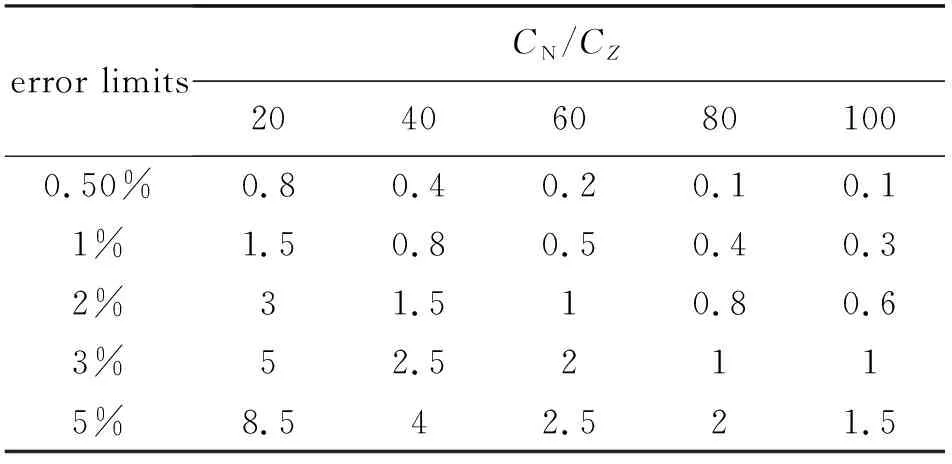
表5 侧向力测量相对误差对滚转角允差/(′)Table 5 Roll angle tolerance in lateral force measurement/(′)

4 结论及结束语

4.1 结论

本文针对安装角误差对压电天平校准结果影响进行了初步分析, 研究结果表明: 天平安装角误差对天平不同校准系数的影响是不同的. 通过研究可以获得初步结论:

(1)天平的轴向力、法向力、侧向力和滚转力矩的校准, 只要攻角度误差小于2.55°, 它引起的砝码加载相对误差小于0.1%.

(2)校准天平的俯仰力矩和偏航力矩， 攻角误差除了对力的大小产生影响外， 还与加载点距天平校准中心距离大小有关， 力矩校准对于攻角误差控制的要求达到几分量级. 加载点偏离天平校准中心从而增大力臂， 可以降低对攻角误差控制的要求.

(3)校准天平法向力对轴向力干扰系数, 即使将相对误差控制放宽至1%, 对于给定天平轴向力主系数与法向力对轴向力干扰系数之比范围(40～100), 要求相应的攻角误差为0.34′～0.08′; 从测量过程分析, 如果将测量的相对误差控制同样为1%, 风洞实验测量中法向力系数与轴向力系数之比范围为5～25, 天平校准时攻角允许误差范围是7′～1.6′.

(4)校准法向力对侧向力干扰系数, 从校准过程分析, 对于给定天平轴向力主系数与法向力对轴向力干扰系数之比范围(40～100), 要求相应的滚转角范围为0.42′～0.17′; 从测量过程分析, 如果控制这个误差小于1%, 通常要求这个滚转角误差小于0.3′.

4.2 结束语

为了解决两个安装角度差别对气动力测量的影响, 提出了解决方案: 对于滚转角差别, 由于通过加工的办法, 在风洞中完全消除滚转角安装误差相对较困难, 在实验准备期间, 先将天平安装到风洞上, 准确测量天平的滚转角, 校准天平时, 将天平的安装滚转角调整到风洞的安装滚转角[41], 确保天平在风洞实验和校准两个过程中滚转角一致, 再对天平在此滚转角状态下进行校准; 至于攻角的差别, 通过以下3个方面的措施加以解决和克服: 第一, 天平校准时, 通过设置天平以及加载套[42]的水平测量基准, 调整天平以及加载套的攻角为零; 第二, 通过调整滑轮安装座, 使轴向力加载线调整到水平; 第三, 风洞实验时, 准确测量攻角, 实验数据处理时, 考虑这个攻角误差(也就是攻角误差)并给予修正. 通过这样的处理, 实验结果表明: 采取上述综合处理措施是有效的, 解决了小侧向力测量结果异常问题.

致谢特别感谢刘施然、 姜华和林文志等同事参与天平校准、 风洞实验以及进行有益的讨论.