基于CPA方法的串联工业机器人运动学标定精度试验研究
孙大林,乔贵方,,宋光明,温秀兰,宋爱国
(1.东南大学仪器科学与工程学院,江苏南京 210096;2.南京工程学院自动化学院,江苏南京 211167)
0 引言
工业机器人已大规模应用于装配、分拣和焊接等制造领域[1-2]。为使工业机器人能够在高端制造领域中得到更为广泛的应用,要求其具有更高的精度性能。通常衡量工业机器人的精度性能参数主要是重复定位精度和绝对定位精度。“智能机器人”重点专项指出工业机器人应用于高端制造领域时,其绝对定位精度应优于0.05 mm,姿态角应优于0.1°[3]。绝大多数的工业机器人具有较高的重复定位精度,而其绝对定位精度无法满足高端制造领域的精度要求。研究表明离线误差补偿技术能够较好地提升工业机器人的精度性能[4]。
工业机器人的典型误差源主要分为几何参数误差和关节刚度误差等[5],其中几何参数误差约占总误差的80%以上。几何参数的标定方法通常分为误差模型法和圆点分析法。基于误差模型法所辨识出的几何参数与实际结构参数无关,较大程度地受测量点空间分布的影响,并且此方法耦合了多种的误差因素,无法进一步地提升工业机器人精度性能[6]。圆点分析法又称为轴线测量法,该方法利用机器人空载时单轴逐一旋转获取轴线方向向量,进而计算几何参数。CPA方法相对误差模型法的优势在于其标定结果与实际结构参数直接相关,能够将几何参数误差与其他误差因素进行分离解耦。萨拉戈萨大学J.Santolaria等人基于CPA方法将KUKA KR-5机器人的定位精度从0.40 mm提高到0.11 mm[7];上海大学张旭等人基于CPA方法将安川MH80机器人的定位精度从2 mm提高至0.7 mm[8]。萨拉戈萨大学J.Santolaria等人[9]和天津大学曲兴华教授等人[10]针对基于CPA的几何参数辨识精度的评价方法开展了初步研究,并指出基于CPA方法的几何参数标定精度受测量策略的影响较大,但目前尚无相关文献讨论CPA方法的测量策略对其标定精度的影响规律。
因此,本文针对基于CPA方法的串联工业机器人运动学标定技术的精度和测量策略展开试验研究。首先介绍了工业机器人的CPA标定方法的基本流程;然后通过实验分别分析了靶球安装位置、关节测量步长、关节测量范围、关节测量点分布位置、末端负载以及初始构型对于CPA标定精度的影响;最后通过分析优化CPA的测量策略,并通过实验验证该测量方案的标定精度。
1 基于圆点分析法的运动学参数辨识
1.1 工业机器人标定系统概述
图1为本文所搭建的工业机器人标定系统。标定系统使用的激光跟踪仪为Leica AT930,在60 m范围内的测量不确定度为±(15 μm+6 μm/m)。配套使用的测量分析软件为Spatial Analyzer软件,该软件提供了包括拟合几何体、建立坐标系等功能。标定系统使用的工业机器人为Staubli TX60机器人,该机器人的重复定位精度为±0.02 mm,额定负载为3 kg,最大负载为5 kg。激光跟踪仪的1.5英寸靶球既可以安装在工业机器人的末端法兰盘上,又可以安装在机器人的连杆上。文中所涉及的测量过程均符合ISO-9283及GB/T-12642-2013 工业机器人性能规范及其试验方法标准。

图1 工业机器人标定系统
1.2 基于CPA的轴线矢量测量及建立坐标系
CPA方法是首先将末端空载或近似空载的工业机器人各关节回到零位,依次单独旋转各关节并利用激光跟踪仪测量机器人各个关节的旋转轨迹,然后根据测量的旋转轨迹数据计算机器人关节轴线的空间坐标,最后依据关节轴线方向和位置计算MDH参数。相比于误差模型方法,基于CPA方法实现的工业机器人参数标定更接近于实际的运动学参数,同时标定过程的计算量相对较少,无需工业机器人名义参数值。

图2 基于CPA的机器人轴线测量及坐标系定义
以固定角度步长依次从负极限位置旋转机器人关节轴1~6到正极限位置,利用激光跟踪仪测量靶球的空间位置,利用SA软件拟合各个关节轴线的空间圆如图2所示,并计算关节轴线Zi的方向向量,根据轴线向量分别建立关节1至关节6的坐标系以及机器人末端工具坐标系,分别用Ai(i=1,2,…,6)和AT表示,各坐标系的轴线表示为Aim(m=x,y,z),坐标系原点表示为Aio。各个关节坐标系的定义依据MDH模型的要求,建立方式如表1所示。
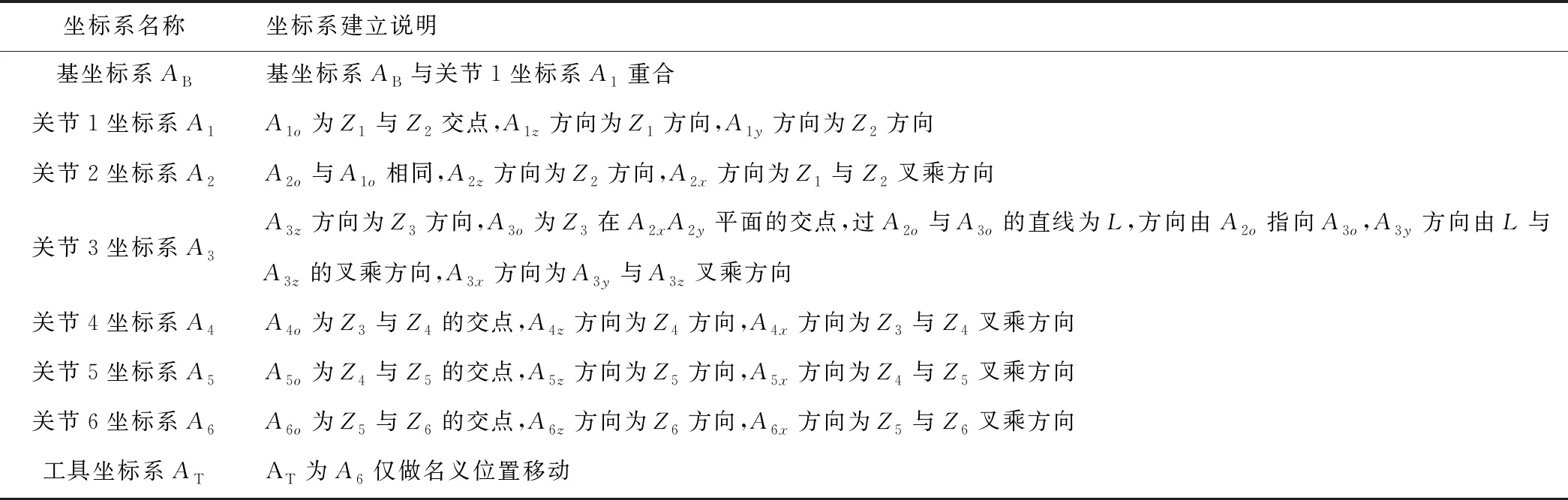
表1 关节坐标系建立过程
1.3 MDH模型参数辨识
经典DH模型在相邻关节近似平行时存在奇异性。而MDH模型通过对近似平行的相邻关节引入绕y轴旋转变换解决了该问题,如图3所示。MDH模型的齐次转换矩阵如式(1)所示。

(1)
式中:θi为Xi-1与Xi之间在绕Zi-1正向上的夹角;di为Xi-1与Xi之间在Zi-1上的距离;ai为Xi-1与Xi之间在Xi上的距离;αi为Zi-1到Zi之间绕Xi正向上的夹角;βi为Zi-1到Zi之间绕Yi正向上的夹角。

图3 MDH模型近似平行关节变换
当相邻关节为非近似平行关节时,βi=0,当相邻关节为近似平行关节时,di=0。
基于图2及表1中所建立的关节坐标系,计算被标定的机器人MDH参数,具体步骤如下:
首先判断Zi-1与Zi是否近似平行,定义ε如式(2)所示,ε≤0.01则认为两轴近似平行。
ε=|Zi-1-Zi|
(2)
如果不近似平行则β=0,计算θ为Xi-1与Xi之间在绕Zi-1正向上的夹角:
(3)
计算a为Z(i-1)o与Zio之间在Xi距离:
(4)
计算d为Z(i-1)o与Zio之间在Zi-1上的距离:
(5)
计算α为Zi-1到Zi之间绕Xi正向上的夹角:
(6)
如果近似平行则d=0,计算θ为Xi-1与A(i-1)oAio间在绕Zi-1正向上的夹角:
(7)
计算a为Z(i-1)o与Zio之间的距离:
a=|Oi-Oi-1|
(8)
计算α为Zi-1到Zi之间绕Xi正向上的夹角。计算βi为Zi-1到Zi之间绕Yi正向上的夹角:
(9)
(10)

为验证以上方法计算MDH参数的精度,本文首先通过SA软件计算相邻关节坐标系的齐次转换矩阵,与式(1)联立后,通过数值拟合法[11]计算出MDH参数,但此方法无法充分反映机器人的结构特性。辨识结果表明2种方法得到的MDH参数基本一致,仅θ3,β2,a4和d3参数计算存在误差,其中Δθ3=Δβ2=0.000 1 rad,Δa4=0.000 1 mm,Δd3=0.005 4 mm。如图4所示,基于几何计算的MDH参数精度相对较低,但该参数充分反映了工业机器人的实际构型,符合CPA方法的特点。

图4 2种建模方法参数计算的精度对比
2 CPA参数标定的误差源分析
为了分析影响CPA法标定精度的主要因素,本文通过控制变量法进行对比实验,分析串联机器人的最优CPA测量策略。定义标准实验条件如下:
(1)机器人处于零位状态,即各轴初始位置均为0°;
(2)靶球安装放置于机器人末端;
(3)各关节的测量步长为2°,即相邻测量点所对应的关节角度的差值为2°;
(4)受限于靶球的接收范围,关节1、4、6的最大测量范围均为[-180°,180°],关节2、3、5的最大测量范围分别为[-5°,127°]、[-5°,142°]、 [-5°,125°]。
为了评价基于CPA方法得到的机器人运动学模型精度,本文在机器人前侧和左侧均任意测量了50个点进行精度验证,如图5所示。前侧点集和左侧点集均分布在60×60×60 cm3的立方体区域内,标定前机器人平均定位误差如图6所示。

图5 前方点集与左侧点集对应测试区域

图6 标定前机器人在前侧和左侧区域的平均定位误差
2.1 靶球安装位置对标定精度的影响
激光跟踪仪的靶球安装位置分为:安装于机器人的末端法兰;分别安装于机器人的连杆上。但由于关节1、4、5、6的连杆较短,通常仅关节2、3安装在连杆上,安装位置如图1所示。其余测试条件为标准测试条件。2种测试方案的模型精度如图7所示,从图7可以看出,2种靶球的安装方案的模型综合误差的差值为0.003 7 mm,对X、Y、Z3个轴向误差的影响也较小。因此,在标准试验条件下,靶球安装位置对CPA的标定精度基本无影响。

图7 连杆位置与末端位置的CPA标定精度
2.2 关节测量步长对标定精度的影响
基于CPA方法的机器人参数标定精度主要受关节轴线拟合精度的影响,因此各个关节的测量步长会对CPA标定精度产生影响。本文将各个关节的测量步长分别改为1°、2°、5°进行CPA标定实验,其他测试条件为标准实验条件,结果如图8所示。可以看出,随着关节测量步长的增加,基于CPA的机器人参数标定精度逐渐提升。其主要原因是过多的测量点会引入测量误差,从而导致机器人标定模型的精度下降。

图8 关节步长大小对CPA标定精度的影响
2.3 关节测量范围对标定精度的影响
测量点的空间圆形轨迹拟合受关节测量范围的影响,通常测量范围达到360°时,拟合空间圆和关节轴线的精度最好。受激光跟踪仪的站位影响,仅部分关节能够实现全范围测量。本文在标准实验条件下,将关节4的测量范围以30°为步长,逐渐增加测量点范围,分别拟合计算空间圆和关节轴线,并与全范围所拟合的圆和轴线进行比较,实验结果如图9所示。从图9可以看出关节测量范围达到90°时,拟合精度已基本不变。
2.4 末端负载对标定精度的影响
基于CPA的机器人参数标定要求机器人末端为空载,但实际测量过程中由于末端需安装测量设备,不能实现理想空载。因此,需讨论末端负载对CPA标定精度的影响。测量标准实验条件下,靶球及其安装工具的总质量是m=1.054 kg,本文实施的对比方案在机器人末端额外增加1 kg砝码,分别进行CPA参数标定,对比结果如图10所示。从图10可以看出,末端负载较低时CPA的标定精度越高,因此,当采用CPA标定方法时,应尽量降低机器人末端测量工具的质量。

图10 负载大小对CPA标定精度的影响
2.5 关节测量点分布位置对标定精度的影响
因受激光跟踪仪与机器人的相对位置影响,各个关节的测量范围会有较大不同。根据文献[12-13]可知,工业机器人的关节角度误差具有位置特性。因此,关节测量点的分布位置会影响CPA的标定精度。在标准实验条件下将关节2、3的测量角度均分为区域Ⅰ、Ⅱ、Ⅲ,如图11所示。使用不同区域的数据拟合关节2与关节3的轴线向量,并计算MDH参数,结果如图12所示。从图12可知,当关节2与关节3均处于区域Ⅰ时,CPA标定精度相对较高。尤其是当处于区域Ⅰ时,经CPA方法标定后的机器人在y轴方向的误差最小。

图11 关节2,3关节测量角度范围区域
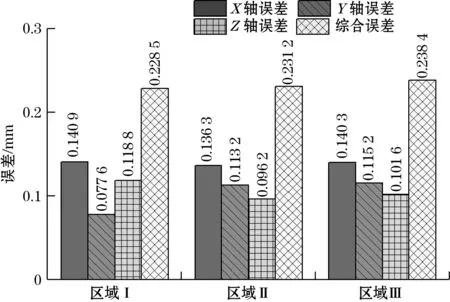
图12 关节点测量范围对CPA精度的影响
2.6 机器人初始构型对标定精度的影响
不同厂家生产的机器人初始构型不同,典型的CPA方法要求工业机器人在测量过程中各个关节应保持在零位位置。目前市场上的主流零位构型如图13所示:分为关节3初始角度为90°,本文称为90°构型,关节3初始角度为0°,本文称为0°构型。不同零位构型在标准实验条件下进行CPA标定结果如图14所示,90°构型的精度高于0°构型。

图13 两种典型的初始构型

图14 初始位姿构型对CPA精度的影响
3 基于CPA的最优测试方案讨论与实验
根据文献[14]可知,串联型工业机器人的末端负载及连杆自重对其定位精度影响较大。根据2.4节的实验结果可知有效降低关节负载可以提高CPA方法的标定精度。文献[15]指出机器人关节2、3受自重和负载影响较大,根据2.1、2.5和2.6节的实验结果综合分析,CPA法的误差较大程度地受关节2、3负载转矩的影响。当机器人末端负载变化前后,不同构型状态下关节2的轨迹误差如图15所示。其中0°构型的综合位移为0.114 4 mm,90°构型的综合位移偏差为0.071 mm,3个轴向上90°构型的轴向位移偏差相比于0°构型分别减少了0.024 mm,0.058 mm,0.038 mm。以上位移偏差会导致关节2的方向向量计算存在较大误差。为方便观察误差方向,图中误差已放大1 000倍。因此,通过调节构型降低关节负载转矩,能够有效地改善轴向向量的测量精度。


图15 不同构型下机器人末端负载对CPA的影响
基于以上试验结果分析,确定CPA法的优化测量策略为:
(1)靶球安装放置于机器人末端法兰,方便测试安装;
(2)各轴初始位置均为0°,仅关节3的初始位置为110°,尽可能减少关节2受到的转矩;
(3)各关节的测量步长为5°,减少测量误差的引入;
(4)机器人关节1~6的测量范围分别为(-90°,90°)、(-45°,45°)、(-5°,125°)、(-90°,90°)、(-5°,125°)、(-180°,180°),在扩大关节测量范围的同时,降低关节2、3所受的转矩。
CPA法与误差模型法的标定精度如图16所示。经CPA法标定后的机器人平均误差为0.182 7 mm,相比于标定前误差减少了43.99%。基于误差模型法标定后的工业机器人的平均误差仅为0.124 1 mm,标定效果比CPA法好。但从图16可以看出,基于误差模型法标定后的机器人模型精度在不同区域内的相差较大,前侧点集的平均综合误差是左侧点集的4.84倍,而CPA法仅为1.67倍,从而说明经CPA法标定的机器人具有较好地全局定位精度。

图16 不同标定方法得到的模型误差
4 结论
本文通过实验研究基于CPA方法的串联工业机器人标定技术,通过试验研究各轴测量角度范围、各轴测量步长、初始位姿构型、靶球安装位置等不同测量策略对CPA标定精度的影响。最终确定CPA方法中的测量关节角度步长应在5°左右,关节角度范围应大于90°,应尽量选择能够减小关节2、3关节转矩的测量构型,实验研究表明,采用优化后的CPA标定方法,被标定机器人的误差减少了43.99%,明显优于其他测量方案。同时研究发现相比于误差模型法,通过CPA方法标定的机器人具有更好的全局定位精度。未来研究工作主要是针对关节刚度误差补偿展开研究,降低关节刚度误差对几何参数标定及工业机器人绝对定位精度的影响。

