期权对我国豆粕市场期现无套利区间的影响

陈新华，刘 洁

期权对我国豆粕市场期现无套利区间的影响

陈新华，刘 洁

（仲恺农业工程学院，广东 广州 510225）

文章基于大连商品交易所和wind等数据库2014—2018年豆粕市场的价格数据，利用三阶段门限自回归模型和合成控制法分析了豆粕期权上市对于豆粕期现无套利区间的影响。研究结果显示：首先，我国豆粕期现无套利区间较宽且随季节性变化明显，套期保值的基差风险较大；其次，豆粕期权上市后我国豆粕期现无套利区间趋于缩小；最后，期权对于不同流动性期货合约期现无套利区间产生的影响存在差异，活跃性较小的合约受到的影响更为显著。

无套利区间；门限回归；合成控制法；期权

一、引言

自1990年正式引入期货交易机制以来，我国期货市场在近三十年的探索中不断发展，其风险规避的功能日益显现，服务国民经济的能力不断增强。期货市场套期保值的主要原理是将较大的价格波动风险转移为较小的基差风险。但是，由于我国期货市场的价格发现水平有限，使得基差的剧烈波动给风险规避带来了极大的不确定性。那么，面对基差风险，套期保值者应该如何应对？近年来，国内多位学者开始关注利用动态套期保值的方法减少基差风险。如张跃军[1]等利用GED-GARCH模型求出燃料油现货和期货收益率的动态标准差，并建立了动态的最小方差套期保值模型，通过对比发现该方法比传统模型的套期保值有效性提高了32.1%；徐荣[2]等构建了基于最优衰减因子时变方差EWMA模型的动态套期保值方案，通过实证检验发现其套期保值效果要优于传统的静态套期保值模型。但是目前学术界对于动态套期保值的实证研究并未形成一个权威、统一的方法。此外，动态的交易策略对于农户和企业等套期保值主体而言不易理解，导致其在实践运用中难以有效地推广。

为了提高期货市场价格发现能力，增加市场流动性及降低市场被操纵的可能性，自2017年率先推出豆粕期权后，我国的商品期权市场发展步入快车道。那么豆粕期权上市4年多来到底对豆粕期货市场产生了什么样的影响，是否有助于其风险规避能力的提升？目前学术界关于期权对期货市场影响的研究主要集中在定价效率和波动率两方面。如吴雯雯[3]认为在股指期权推出以后减少了股票投资者情绪对于股票价格的影响，同时金融市场的产品类型越丰富越能保护投资者权益、降低投资者的风险。王伟[4]分析我国白糖期权和期货市场的数据后认为，期权的推出可以减少期货价格被高估的概率。国内外学者关于期权对于期货波动率影响的研究中，较多的观点支持期权上市交易会对期货市场的波动率产生明显的抑制作用。如缴建巍[5]基于2014年6月至2018年3月我国豆粕期货和白糖期货价格数据，利用GARCH模型并通过引入虚拟变量的方式，分析了豆粕期权和白糖期权对我国期货市场价格波动率的影响，得出的结论是期权上市后抑制了相关期货价格的波动率。郭若宇[6]利用ARMA-GARCH模型就豆粕期权上市对豆粕期货价格波动性的影响进行了实证分析，并认为期权上市改善了期货市场的运行状况，减少了市场波动。持相同观点的还有莫媛、方龙等[7–11]。但是，基差风险除了受定价效率和波动率影响外，还有一个核心影响因素就是无套利区间的范围。当基差波动到无套利区间外时，套利者的介入会改变期货和现货市场的供需关系，使得基差重新回归到合理的区间之内。因此，一个期货市场期现无套利区间的大小决定了套期保值者面临基差风险的大小。那么，期权上市对于期货无套利区间会产生什么影响，是否有助于减少套期保值的基差风险，从而促进期货市场规避风险能力的提升？目前学术界还未对此问题展开深入的探讨。

基于以上背景，本文选取了2014—2018年豆粕等期货合约的价格数据，并运用三阶段门限自回归模型和合成控制法分析了豆粕期权上市对于豆粕期现市场无套利区间的影响，研究的结论能够对提高我国期权及期货市场的有效融合及良性互动带来一定的启示。

二、理论分析与研究假设

期货市场套期保值的原理是利用期货市场的盈利弥补现货市场的亏损，把较大的市场价格风险转移为较小的基差风险，多头和空头套期保值者利用期货市场的保值结果分别如式（1）和（2）所示：

其中S表示某标的资产的现货价格，F为期货价格，L代表基差，t为当前时刻，T为期货到期日。由此可见，套期保值的风险取决于基差的波动幅度。根据无套利定价原理并且引入便利收益后，可以得到基差表达式如式（3）所示：

其中r为期货合约有效期内的无风险利率，c为以现货价格一定比例表示的仓储成本和保险费用，y为以现货价格一定比例表示的边际便利收益。豆粕基差的变动可能会受到贸易政策、相关产品价格波动及投资者的供需预期等因素的影响，呈现出正向市场和反向市场的反复交替。但是由于无套利区间的存在使得基差的波动幅度受到了套利活动的限制，如果基差的波动超过了无套利区间的下限，套利者可以通过卖空期货合约同时买入现货构造一个资产组合来进行套利，当基差的绝对值高于套利成本之和则可以获利；如果基差超过无套利区间的上限，套利者则可以进行反向套利。套利者的介入会改变现货市场和期货市场的供求关系，从而促使基差回归到一个合理的区间内。我国期货市场的套利者相对于投资者的数量较少，套利行为不仅取决于资金占用成本、现货的仓储成本及保险费用等期现套利成本的大小，还受到投资者对于未来供需的预期及市场流动性等因素的影响。这些变量会随着时间推移而发生改变，导致不同时期的套利行为的触发条件存在差异。

基于以上分析，本文提出第一个研究假设：我国豆粕市场的期现无套利区间会随着时间发生改变。

那么，期权上市又会对其产生什么样的影响呢？诺贝尔经济学奖获得者Black和Scholes（1973）证明了风险中性定价原理下，期权定价公式可以表达为式（4）：

其中c表示t时刻的期权价格，S表示t时刻的标的物价格，K为行权价，T为到期日，r为期权合约有效期内的无风险利率，σ为标的资产的收益波动率，N表示正态分布。式（4）表明，t时刻的期权价格是关于S、K、r、T和σ的函数。因此，可以根据市场所反映出来的期权价格推导出从t时刻到T时刻的预期波动率，即隐含波动率。隐含波动率σ反映了人们对标的资产未来波动率的预期。由于我国豆粕期权的标的物并非实物资产而是标准化的期货合约。假设期权行权后的期货合约最后都会进行实物交割，并且忽略期权行权日和期货最后交割日之间保证金所产生的资金使用成本，可以根据Put-Call Parity公式构建一个平价状态下的期权和期货价格关系式，如式（6）所示：

其中，C表示豆粕看涨期权，P表示豆粕看跌期权，F为当前豆粕期货合约的价格，S表示豆粕现货价格，I为现货资产的存储成本的现值。由式（6）可见，受期权价格影响，期货和现货价格差波动存在一个无套利区间。因此，套利行为会限制不合理的基差进一步扩大，使得其波动幅度逐渐变小[12]。

由此可见，期权对于期现无套利区间的影响主要体现在以下两个方面：第一，隐含波动率会传递到期货价格的波动中并对其产生持续影响。当期货市场出现较浓的投机氛围时，期权和期货市场间的联动性会对期货市场的持续非理性投资情绪产生一定的缓解作用；第二，当基差波动剧烈时，套利者可以通过构造包含期权、期货和现货的资产组合来获取风险相对较小的套利收益，使得投资者的套利行为更为多样化。

基于以上分析，本文提出的第二个研究假设：豆粕期权的上市有助于缩小豆粕市场期现无套利区间的大小。

三、研究方法

（一）三阶段门限自回归模型

理论上的无套利区间的大小等于资金占用成本、仓储成本及保险费用等期现套利成本的和，但是投资者的套利行为还会受到对未来供需预期及市场流动性等诸多因素的影响，使得期现的套利区间存在一定的波动性。考虑到套利者自发的逐利性，本文试图利用投资者的市场交易行为所反映出来的基差均值回复现象，来分析不同时期无套利区间的大小[13‒14]。基于此，下文将首先利用三阶段门限自回归模型对我国豆粕市场基差的均值回复机制进行研究。该模型曾被用于分析经济存在加速扩张、平稳发展和迅速衰退3个不同时期时所反映出来的特点和失业率的动态非对称性问题[15–16]。其结构方程如式（8）所示：

式（8）中，r和r分别表示三阶段门限自回归模型中的上、下门限值。当基差处于无套利区间外时，套利者的交易行为会改变前期基差对于当期基差的影响系数。因此，可以利用该模型来识别出我国豆粕市场不同时期的无套利区间的上、下限。

（二）合成控制法

要分析期权上市对于基差无套利区间影响的一个最简单的方法就是考察期权上市前后该时间序列的变化情况。但是，即使基差无套利区间发生了变化也不能表明一定是期权上市所产生作用的结果，还有可能受原有变化趋势影响或其他混淆事件作用，如经济周期、市场规模及政策环境等因素。为此，可以使用Abadie and Gardeazabal（2003）提出的“合成控制法”（Synthetic Control Method）对此问题进行分析。

具体研究思路如下：假设共有（1+J）个期货品种，其中第1个为有期权上市的品种（即豆粕期货），而其余J个期货品种构成潜在的控制组，称为“donor pool”。在豆粕期权上市之前，豆粕期货各预测变量的平均值为向量X，将未有期权上市的其他期货品种相应预测变量的平均值记为矩阵X，其中第列为第个期货品种的相应取值[20]。

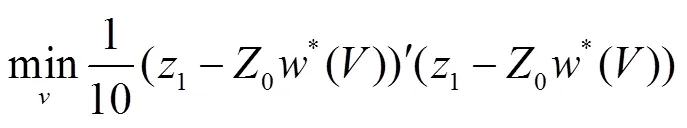
借鉴国内对基差影响因素的相关研究成果[17‒19]，本文所选取的预测变量包括：流动性、投资者情绪、持仓收益波动及库存量。因为，豆粕期货是我国农产品期货中交易量最大的品种，所以，本文用成交量和持仓量的比值来代替其流动性，投资者情绪用每日的最高价和最低价的平均数来表示，持仓收益波动则用豆粕期货涨跌1和涨跌2的方差来表示。为了更多地反映经济基本面情况，本文选择豆粕的社会库存，而非交易所库存数据。显然，我们希望选择权重能使得Xw尽可能地接近于X。即经过加权之后，合成控制期货品种的价格波动特点尽量和豆粕期货相似。此最小化问题的目标函数是二次函数，记此约束最小化问题的最优解为（）。以最小化“均方预测误差”（Mean Squared Prediction Error，简记MSPE）的方法将每期的预测误差平方后再求各期的平均，并通过求解最小化得到构成合成豆粕期货的最优权重，* =*（*）。

一个潜在假设是豆粕期权的上市不会对其他的期货品种的价格波动产生影响。因此，通过加权后得到的合成期货合约模拟了假设豆粕期权未上市的情况下豆粕期货价格波动的情况，两者之间的差异就是期权上市对于期货价格波动的影响。

四、实证分析与稳健性检验

（一）期权对期现无套利区间影响的实证分析

为了利用三阶段门限自回归模型和合成控制法分析豆粕期权上市对于豆粕期现无套利区间的影响，本文选取了2014—2018年大连商品交易所豆粕期货每日收盘价，并采取了主力换月的规则获得了连续的期货合约的日度价格；现货价格方面，选取了东莞、江苏、天津及山东豆粕市场现货的平均价格作为计算依据。得到的基差价格的基本统计特征数据如表1①所示。

数据来源：大连商品期货交易所、wind数据库及天下粮仓（www.cofeed.com）。

从表1基差的基本统计特征可以看出，豆粕基差的偏度和峰度分别为0.331和2.799，JB值为36.176，表明其分布与正态分布差异较大。最大值和最小值分别为186和-213，均值为16.467，表明我国的豆粕期货长期处于反向市场，而且其和现货价格差值的波动幅度较大。进一步对基差进行平稳性检验，结果如表2所示。

由表2可以看出，ADF统计值为-6.821，基差通过了1%显著性水平下的平稳性检验。

接下来对该时间序列可能存在的门限数量和门限值进行了估计，结果如表3和表4所示：

表3 门限数量检验

表4 上、下门限值估计

根据表3的检验结果发现，单一门限模型和双门限模型都通过了1%的显著性检验，而三门限模型未能通过5%水平的显著性检验，因此豆粕基差序列表现出了较强的双门限特征。为了对比期权上市前后我国豆粕市场基差时间序列的波动情况，进一步分别检测出期权上市前后的上、下门限值进行对比。结果如表4②所示。

基于表4的结果可以发现，在豆粕期权上市之前豆粕基差无套利区间的上、下限分别为87.489和-80.506，而在豆粕期权推出后该区间缩小为70.175和-71.437。

从图1中则可以更为直观地看出：豆粕基差的无套利区间在豆粕期权上市后明显缩小。近年来，我国的大豆进口来源国开始呈现出多元化的特点，南美进口大豆的充沛供应以及国内油厂持续的高压榨量导致2018年度我国豆粕市场的负基差较2017年延续的时间更长，豆粕市场长期期现倒挂的现象有所缓解，同时也使得豆粕基差无套利区间的上限出现了明显的下移。在豆粕期权推出之后，我国豆粕市场基差出现不理性波动的频率在减少、幅度也在减弱。但是，两个周期内的宏观经济形势、投资者规模及市场情绪都发生了很大的差异，这些都会对豆粕基差的波动产生影响；尤其是2018年开始的中美贸易争端对于大豆及其相关副产品的价格波动产生了持续的影响。要准确判断期权上市对于豆粕市场基差无套利区间的影响，还必须排除其他因素的干扰。

图1 期权上市前后我国豆粕市场基差时间序列的波动情况

下文将继续基于“合成控制法”（Synthetic Control Method）关于期权上市对于期货期现无套利区间的影响进行实证检验。考虑到上市交易时间的长度、上下游产业的相关性和替代性，交易规则的相似性等因素，本文选取了我国大连和郑州商品交易所的玉米、豆一、豆油、棕榈油和鸡蛋等九个期货品种作为豆粕期货的控制组③。各预测变量的数据也来源于大连商品期货交易所和郑州商品交易所。以季度为时间单位，利用三阶段自门限回归模型计算出各期货品种的无套利区间上、下限绝对值合的时间序列，并利用合成控制法得到各控制组期货品种所占权重的模拟结果如表5所示。

表5 各控制组期货品种所占权重

数据来源：大连商品期货交易所及郑州商品交易所。

由表5，玉米、豆一、豆油、棕榈油、鸡蛋、油菜籽、菜籽油、菜籽粕及早籼稻所占比重分别7.9%、42.7%、13.8%、0.01%、6.3%、10.2%、9.8%、0.7%和8.3%。其中豆一期货所占权重最大，达到了42.7%，因为豆粕是大豆的主要副产品，因此两者表现出了较为接近的价格波动状态。棕榈油所占比重最小，仅为0.01%。

由表6的对比结果可以看出，合成豆粕期货与豆粕期货的流动性、投资者情绪及库存量等预测变量拟合效果分别达到了108.1%、111.5%、106.3%、88.3%和91.6%。将合成豆粕期现无套利区间上、下限绝对值的和所产生的时间序列和我国豆粕市场真实的数据进行对比结果如图2所示：

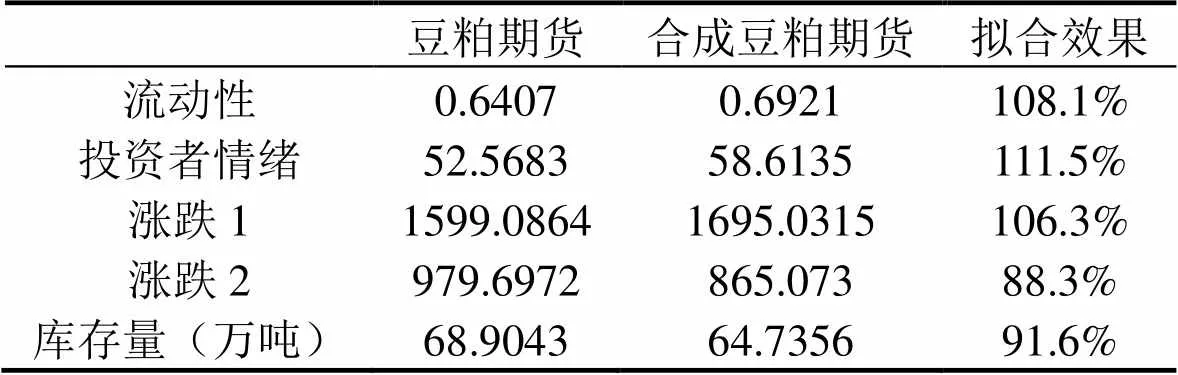
表6 预测变量对比

数据来源：同表5。

图2 合成控制的对比结果

由于我国期货市场农产品期货品种的数量相对较少，导致合成豆粕期货与豆粕期货的拟合效果不是特别理想，而且由于豆粕期权的推出时间较晚，使得上市后基差波动的观测值较少。但是通过图2仍然可以较为直观的判断：期权上市后，豆粕基差无套利区间的幅度相对合成豆粕出现了缩小。

（二）稳健性检验

为证实结果的有效性，验证实证分析中期现无套利区间差异确实是源于期权上市的影响而非其他因素，下文将采用安慰剂检验法对实证估计的显著性进行检验。首先，将相关的其他期货合约品种也都进行合成控制法的模拟，取豆粕期权上市后各期货品种的MSPE与上市前的MSPE的比值（MSPE衡量了一个期货品种与其合成控制对象之间的拟合量级差异度），并与豆粕期货进行对比。其基本逻辑如下：如果所有的期货合约基差波动都在豆粕期权上市后（2017年3月）发生了显著的变化，则仍然无法证明期权上市后对于期现无套利区间产生了显著的影响。

除了上文提到的油菜籽、鸡蛋、豆油及鸡蛋等九个在控制组变量中的合约品种外，还增加了不活跃交割月份的豆粕期货合约，引入了不活跃交割月份的合约的原因是农产品期货有向主力合约交易集中的特点，因此，期权的上市有可能会对不同流动性的期货合约基差波动产生不同的影响④。对上述10种期货合约品种分别进行合成控制法并与豆粕期货的结果进行了对比分析。安慰剂检验的结果如图3和图4所示。

从图3可以看出，相对于其他九种农产品期货品种，两种豆粕期货合约在期权上市前后的基差无套利区间发生了更为显著的变化。期权对于非活跃月份豆粕期货基差的影响比对主力合约的影响更大，主要原因可能是大量的做市商在进行期权交易的同时，会使得非活跃月份期货合约的流动性增加更为明显，从而提高了相应期货合约的定价效率。

图3 各期货品种合成控制结果的对比

从图4可以看出，期权上市前后，豆粕期货与其合成控制对象之间的拟合度差异要大大高于其他参照期货品种。除此之外，大豆期货和豆油期货前后的比值也相对较高，出现这种情况的原因有可能是豆粕期权的上市对于与豆粕价格相关性最高的大豆和豆油的期货价格波动也产生了影响。安慰剂检验的结果进一步证明了豆粕期权上市对于豆粕市场期现无套利区间产生了显著的影响。

图4 各期货品种期权上市前后MSPE比值的结果

五、研究结论与启示

本文基于大连商品交易所、郑州商品交易所和wind等数据库2014—2018年豆粕等期货合约的价格数据，利用三阶段门限自回归模型和合成控制法分析了豆粕期权上市对于豆粕期现无套利区间的影响。研究结果显示：首先，我国豆粕期现市场无套利区间较宽且随季节性变化明显，套期保值的基差风险较大，其次，豆粕期权上市后使得我国豆粕期现市场的无套利区间趋于缩小；最后，期权对于不同流动性期货合约的期现无套利区间产生了不同的影响，对活跃性较小的合约期现无套利区间的影响更为显著。基于实证分析的结论，提出以下几点政策启示：

1. 提高期货交易者的交易技巧，鼓励机构投资者套利交易。我国豆粕期货市场长期处于反向市场状态，而且期现无套利区间上、下限较宽，导致套期保值者的基差风险较大。产生这种现象的原因可能由两点：首先，我国的大豆生产自给率较低，产生了较大的便利收益预期；其次，我国期货市场的投机性氛围较浓厚，导致期货价格经常会偏离合理区间。因此，应当加大期货市场参与者的培训力度，提高期货交易者的交易技巧，同时鼓励机构投资者套利交易，提高我国期货市场价格发现的能力。

2. 继续有序地加快期权市场的建设速度，增加我国金融衍生品市场深度。期权上市对于基差无套利区间产生了较为显著的影响，减少了套期保值的基差风险；同时也为需要在期货交易的不活跃月份中进行风险规避的交易者提供了多样化的选择方式。我国应当有序地加快期权市场的建设速度，提高期权和期货市场有效融合，建立符合我国市场需要的多层次的风险规避金融体系，提高金融衍生品服务实体经济的能力。

① 本文选取的基差等于现货价格与最近的主力期货合约价格的差。

② 根据AIC准则检验，本文最终选择了滞后阶数为1的模型，这也与期货市场套利者的逐利性的特点相吻合。

③ 其中，豆一、豆油、棕榈油和鸡蛋等都未有对应的期权合约上市；虽然玉米和菜籽粕已经推出了期权，但是时间分别是在2019年的1月和2020年1月，因此，也不会对本文的检验结果产生影响。

④ 受国内大豆和进口大豆集中上市的影响，每年10月国内压榨商进入了生产和避险的高峰期，因此，本文选取10月份交割的豆粕期货合约作为不活跃的合约的代表。

[1] 张跃军, 涂鋆. 中国燃料油期货市场动态套期保值研究——基于Copula-GARCH模型的实证分析[J]. 北京理工大学学报（社会科学版）, 2015（1）: 8‒13.

[2] 徐荣, 李星野. 基于EWMA模型的铜期货动态套期保值效果研究[J]. 经济数学, 2018（1）: 86‒89.

[3] 吴雯雯. 期权推出对期货定价有效性的影响——基于沪深300指数期货和期权的研究[D]. 济南: 山东大学, 2015.

[4] 王伟. 我国白糖期货期权推出对白糖期货市场定价效率的影响研究[D]. 乌鲁木齐: 新疆财经大学, 2018.

[5] 缴建巍. 豆粕和白糖期货期权对标的市场波动性的影响研究[D]. 保定: 河北大学, 2018.

[6] 郭若宇. 豆粕期货期权上市对豆粕期货市场波动性影响的实证分析[D]. 成都: 西南财经大学, 2018.

[7] 莫媛, 方龙. 股指期权对股票市场、股指期货市场波动性影响[J]. 当代经济, 2016（27）: 90‒93.

[8] 张静, 宋福铁. 上证ETF50期权上市对标的股票的影响——基于流动性和波动性的视角[J]. 金融发展研究, 2016（3）: 59‒65.

[9] 庞贞燕, 刘磊. 期货市场能够稳定农产品价格波动吗?——基于离散小波变换和GARCH 模型的实证研究[J]. 金融研究, 2013（11）: 126‒139.

[10] P. Srinivasan. Do futures and options trading increase spot market volatility in India? The case of S&PCNX Nifty[J]. International Journal of Business Performance and Supply Chain Modelling, 2010, 2（2）: 134‒145.

[11] 徐金剑. 股指期权对标的指数波动性的影响[D]. 青岛:青岛大学, 2016.

[12] 赵志成. 金属期权交易对金属期货市场的影响: 基于对我国铜期货的研究[J]. 中国矿业, 2019（10）: 86‒90.

[13] 蒋勇. 股指期货基差的非线性特征和均值回复机制研究[J]. 中国科学技术大学学报, 2013, 43（12）: 898‒996.

[14] 孟庆斌, 杨俊华. 基于门限自回归模型的中国财政风险预警系统[J]. 中国人民大学学报, 2016（6）: 89‒96.

[15] 吴武清, 李东, 潘松．三阶段均值回复、TAR及其应用[J]．系统工程理论与实践, 2013, 33（4）: 901‒909．

[16] Koop G, Potter S M. Dynamic asymmetries in U.S. unemployment[J]. Journal of Business & Economic Statistics. 1999, 17（3）: 298‒312.

[17] 叶伟青. 天然橡胶期货基差的影响因素研究[D]. 杭州:浙江大学, 2013.

[18] 徐晓晖. 存货、基差与波动率——对沪铜、铝、锌的实证研究[D]. 北京: 清华大学, 2010.

[19] 方晚秋. 大豆期货基差与流动性关系研究[D]. 开封: 河南大学, 2019.

[20] Abadie A, Diamond A, Hainmueller J. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program [J]. Journal of the American statistical Association, 2010, 105（490）: 493‒505.

The Impact of Options on the Arbitrage-free Interval of Soybean Meal Futures Market in China

CHEN Xin-hua, LIU Jie

（Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong 510225, China）

Based on the price data of soybean meal market from 2014 to 2018, such as Dalian Commodity Exchange and wind database, the paper analyzes the impact of soybean meal option listing on the arbitrage-free interval of soybean meal market by using three-stage threshold regression model and composite control method. The results show that: firstly, the arbitrage-free interval in the soybean meal futures market in China is wide, changing obviously with seasons, and the basis risk of hedging is large; secondly, the arbitrage-free interval in the soybean meal futures market tends to narrow after the soybean meal options are listed; finally, options have different effects on the arbitrage-free interval in different liquidity futures contracts, more visible influence on the contracts with less activity.

arbitrage-free interval; threshold regression; composite control method; options

2021-04-13

教育部人文社会科学研究青年基金项目（18YJC630097）

陈新华（1982—），男，湖北黄冈人，副教授，博士，研究方向：农业经济管理。

F323.7

A

2095-9249（2021）04-0040-07

〔责任编校：王中兰〕