基于ARIMA和LSTM混合模型的时间序列预测

王英伟 马树才

(辽宁大学经济学院 辽宁 沈阳 110036)

0 引 言

时间序列预测在众多领域有广泛应用，如金融、经济、工程和航空等，并成为机器学习领域的重要研究课题[1]。现实中时间序列通常同时具有线性和非线性特征，因此对不同时间序列现象建立模型并准确预测已成为最具挑战的应用之一。

ARIMA等统计模型以简单和灵活性被大量用于时间序列预测[2-3]，但现实中的时间序列通常具有非线性特征，而传统时间序列预测方法是线性模型，在对时间序列建模中表现出一定局限性[4]。因此，支持向量机和神经网络等非线性模型，被广泛用于时间序列预测领域[5]。其中神经网络具有强大的非线性、映射性和自适应性等特征，可以有效提高预测精度，以LSTM为代表的深度神经网络成为近年来的研究热点。但单一非线性模型对同时具有线性和非线性特征的时间序列并不能获得最优结果[6]。

由于单一模型的局限性，众多学者提出由线性和非线性模型组成的混合模型。Zhang[7]和Oliveira等[1]假设时间序列同时具有线性和非线性特征，并分别提出ARIMA-ANN混合模型和ARIMA-SVR混合模型，ARIMA用于提取线性特征，而ANN和SVR用于提取残差特征，最后对两者进行组合，后者应用PSO选择模型参数。文献[8]提出ARIMA-SVR_s混合模型，首先将时间序列分解为高波动率和低波动率两部分，并分别使用ARIMA和AR_SVR对两部分建模，最后将两者结果组合。实验结果证明，混合模型可以有效提高预测精度。以上模型均假设时间序列是线性特征和非线性特征的线性组合,但在实际应用中，两者可能存在非线性关系，从而影响混合模型的性能。

针对上述问题，本文对线性和非线性模型预测结果的组合方式提出新的策略。首先采用ARIMA模型提取时间序列线性特征，然后用SVR模型对ARIMA模型的预测值和实际值间的误差序列进行预测，最后将前两者预测结果作为LSTM模型的输入对时间序列进行预测，并应用贝叶斯优化算法选择深度LSTM模型的超参数。

1 ARIMA模型

ARIMA模型是由Box和Jenkins提出的用于时间序列分析和预测的线性模型。在时间序列分析中，需要设置3个参数，分别为自回归阶数(p)、差分阶数(d)和移动平均阶数(q)，ARIMA(p,d,q)的一般形式如下：

(1)

φ(B)=1-φ1B-φ2B2-…-φpBp

(2)

θ(B)=1-θ1B-θ2B2-…-θqBq

(3)

式中：B为后移算子；▽d=(1-B)d为高阶差分；φi(i=1,2,…,p)和θj(j=1,2,…,q)分别为自回归参数和移动平均参数；εt为符合N(0,σ2)正态分布的误差项。式(2)和式(3)分别为自回归相关系数多项式和移动平均系数多项式。

时间序列yt应先采用ADF检验选取差分阶数，将时间序列变为平稳序列，再根据赤池信息准则(Akaike Information Criterion，AIC)选择最佳模型。

2 支持向量回归

支持向量回归是基于结构风险最小化(SRM)原则进行泛化误差上界最小化，最初由文献[9]提出的机器学习方法。

f(x)=ωφ(x)+b

(4)

式中：ω为权值向量;φ是将样本空间映射到高维空间的非线性变换函数;b为偏差。

为保证支持向量回归具有稀疏性，引入ε不敏感损失函数，允许样本值落入不敏感损失带，即允许最大为ε的误差，公式如下：

(5)

参数ω和b通过式(6)求得。

(6)

s.t.yi-ωφ(x)-b≤ε+ξ

ωφ(x)+b-yi≤ε+ξ*

ξ,ξ*≥0,i=0,1,…,l

式中：‖w‖2为模型复杂度项;C为惩罚因子，用于平衡模型复杂度和最小训练误差;ξ和ξ*表示松弛变量，用以度量不敏感损失带外的训练样本偏离程度。将式(6)引入拉格朗日函数和核函数，则非线性回归函数表示为：

(7)

3 LSTM模型

循环神经网络(RNN)是用于处理序列数据的神经网络。其最大特点是神经元在某一时刻的输出能够作为输入再次输入到神经元，从而使网络具有记忆能力，但RNN无法解决长期时间序列依赖问题。因此，Hochreiter等[10]提出长短期记忆(LSTM)神经网络。

LSTM模型是标准RNN的一种变体，通过引入记忆单元(Memory Cell)解决长期依赖问题，即梯度消失和梯度爆炸[11]，记忆单元结构如图1所示。

图1 LSTM记忆单元图

每个记忆单元包含三个门控结构：遗忘门(ft)、输入门(it)和输出门(ot)，用于对类似传送带的单元状态(Cell State)进行移除和添加信息。每个门控结构由一个sigmoid神经网络层和一个点乘操作组成。假设xt表示t时刻的输入向量，Wf、Ws、Wi和Wo表示循环层权重矩阵，Uf、Us、Ui和Uo表示输入层权重矩阵，bf、bs、bi和bo表示偏置向量，ht表示LSTM层的输出向量，计算过程如下：

1) 通过遗忘门移除单元状态St-1中的无用历史信息，并计算遗忘门激活值：

ft=sigmoid(Ufxt+Wfht-1+bf)

(8)

2) 通过输入门决定将哪些新信息存储到单元状态：

it=sigmoid(Uixt+Wiht-1+bi)

(9)

(10)

3) 将旧单元状态St-1更新为新单元状态St：

(11)

4) 输出门通过sigmoid层决定需要输出的单元状态，并将输出结果Ot和经过tanh层的新单元状态tanh(St)相乘计算记忆单元的输出ht：

Ot=sigmoid(Uoxt+Woht-1+bo)

(12)

ht=Ot⊗tanh(St)

(13)

LSTM神经网络要求输入连续时间步上的特征向量值以便进行训练。假设每个序列共有N个时间步，并且SN表示第N个时间步的特征向量,所以第M个序列可以表示为{SM,SM+1,…,SM+N-1},输入特征向量序列的构造方式如图2所示。

图2 LSTM神经网络的输入特征向量序列构造方式

4 深度LSTM神经网络

深度LSTM神经网络是由多个基本LSTM模块组成，核心思想是在较低LSTM层建立输入数据的局部特征，并在较高LSTM层进行整合。实验证明，深度LSTM神经网络结构的学习能力更强[12]。

图3 深度LSTM网络结构

5 贝叶斯优化算法

贝叶斯优化算法是一种高效的全局优化算法[13]。它能够在每次迭代中，根据代理模型拟合实际目标函数的结果选择最优评估点，减少目标函数的迭代次数，尤其适合对评估代价高昂的黑盒目标函数进行优化，因此被广泛用于机器学习和深度学习的超参数优化。

假设目标函数f:X→R，贝叶斯优化采用基于模型的序贯优化法对式(14)中的最优化问题求解。

(14)

贝叶斯优化算法的迭代过程可以分为三个部分。(1) 根据最大化采集函数选择最优评估点，即xn+1=argmaxap(x)，其中ap(f):X→R为采集函数，p(f)为f的先验概率分布；(2) 评估目标函数yn+1=f(xn+1)+ε，并将新的点(xn+1,yn+1)加入观测数据Dn=(xj,yj),j=1，2，…，n；(3) 更新f的后验概率分布和采集函数，分别表示为p(f|Dn+1)和ap(f|Dn+1)。

本文采用高斯过程(GP)作为代理模型，而采集函数则使用期望提高(Expected Improvement, EI)函数。

6 ARIMA_DLSTM模型

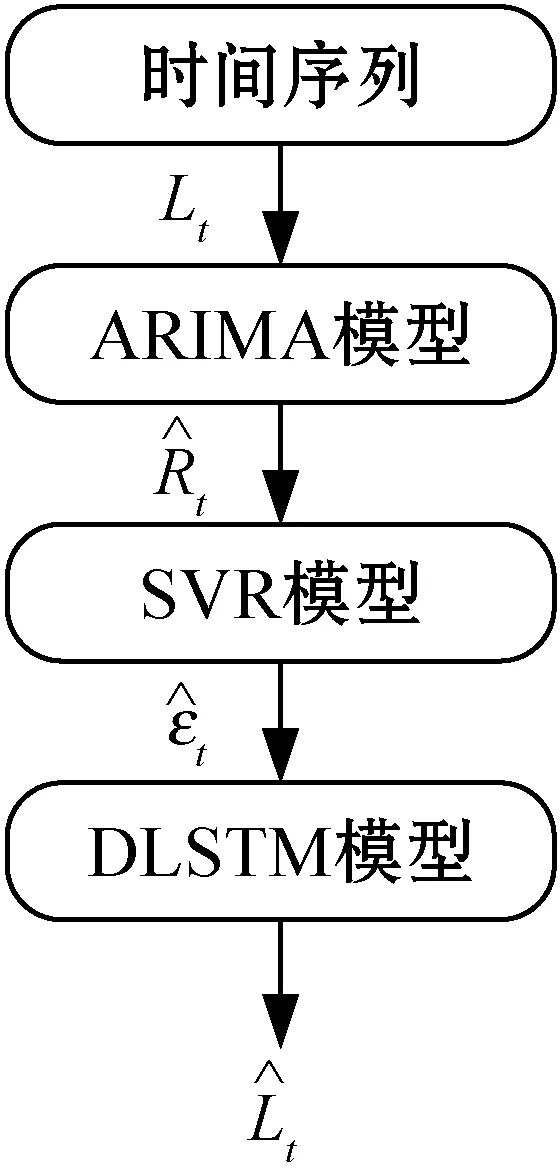
图4 ARIMA_DLSTM模型流程

7 实 验

7.1 实验数据与预处理

本文采用5组来自不同领域的时间序列数据集进行实证研究，分别为Canadian Lynx、Colorado River flow、Airline Passengers、比特币兑美元汇率和国内糖期货价格指数。以上具有不同统计特征的数据集在时间序列预测研究的文献中被广泛应用[7,14-15]。

首先对Canadian Lynx数据集进行对数化处理，即将所有值取常用对数，再对每个数据集按4∶1的比例划分为训练集和测试集，训练集用于训练模型，测试集用于评估模型性能。Canadian Lynx数据集共有114个样本，其中前100个样本作为训练集，后14个样本作为测试集。Colorado River flow数据集共有744个样本，前595个样本作为训练集，后149个样本作为测试集。Airline Passengers数据集共有144个样本，前115个样本作为训练集，后29个样本作为测试集。比特币兑美元汇率采用2014年12月至2019年7月间的数据，共有1 672个样本，前1 472个样本作为训练集，后200个样本作为测试集。国内糖期货价格指数采用2006年3月至2019年4月间共3 190个样本，前3 000个样本作为训练集，后190个样本作为测试集。

在神经网络训练中，数据间的量纲差别对网络训练是否能收敛以及预测准确性起到关键作用[16]。因此，在建模前需要对输入数据进行预处理，本文利用式(15)将样本数据归一化至[0,1]区间。

(15)

式中：minI(t)和maxI(t)分别为训练数据集的最小值和最大值。训练后的输出数据进行反归一化处理，以便得到预测值。

为提高模型泛化能力，采用如下两种方式避免过拟合。首先，采用失活(dropout)正则化，在网络训练的每次更新中，以一定失活率随机选择一部分单元失活，包括输入连接和递归连接，可以有效防止过拟合。如果采用深度LSTM网络，可以同时在每层间采用失活正则化，所以每层网络共有三个失活参数。其次采用早停法，将训练样本划分为训练集和验证集，在每次迭代中，分别计算训练集和验证集的损失值，如果验证集损失值在步数k内不再减少，则停止训练，并返回最低验证损失值的模型参数。本文中使用两层LSTM神经网络，因此共有六个失活参数。在训练集中，80%样本作为训练集，20%样本作为验证集，步数k设置为50。

7.2 衡量指标

为评估ARIMA_DLSTM模型的预测性能，本文采用均方误差(MSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE)作为衡量预测精度的指标。计算公式分别为：

(16)

(17)

(18)

式中：Xt表示实际值;Ft表示预测值;N为时间序列数据集的样本数量。

7.3 实验结果

表1中列出ARIMA_DLSTM混合模型中SVR模型和DLSTM模型的参数及其选择范围。SVR模型采用RBF核函数，超参数包括惩罚系数C、不敏感损失系数ε、宽度系数γ和时间步timestep，可以通过网格搜索进行选择，时间步数为输入序列的长度。DLSTM模型的层数为2，超参数包括每层神经元数量和dropout参数，其中dropout参数包括输入连接、递归连接和每层连接之间失活参数，所以2层网络共有6个参数，并采用贝叶斯优化算法[17]进行超参数选择，算法迭代次数为50。为评估ARIMA_DLSTM混合模型的性能，将ARIMA[7]、ARIMAMLP[18]、ARIMA_MLP[7]、ARIMA_SVR[8]和ARIMA_SVR_s[1]预测模型作为对比模型。

表1 模型参数及取值范围

(1) Canadian Lynx数据集。在SVR模型中，惩罚系数C为1 000，不敏感损失系数ε为0.1，宽度系数γ为1.0，时间步(输入序列长度)为10。LSTM模型的每层神经元个数分别为26和21，dropout为[0.10,0.26,0.16,0.12,0.27,0.26]，时间步为5，迭代次数为2 000次。

图5给出利用贝叶斯优化算法对LSTM模型进行超参数优化的最优验证误差迭代图。可以看出，算法在第42次迭代后误差值最优。

图5 贝叶斯优化算法在Canadian Lynx的验证误差迭代图

表2给出了不同模型在Canadian Lynx时间序列测试集中的预测结果。可见，ARIMA_SVR模型在比较模型中最优，而ARIMA_DLSTM模型的测试结果比ARIMA_SVR模型的MSE、MAPE和MAE值分别降低53.47%、24.84%和26.80%。

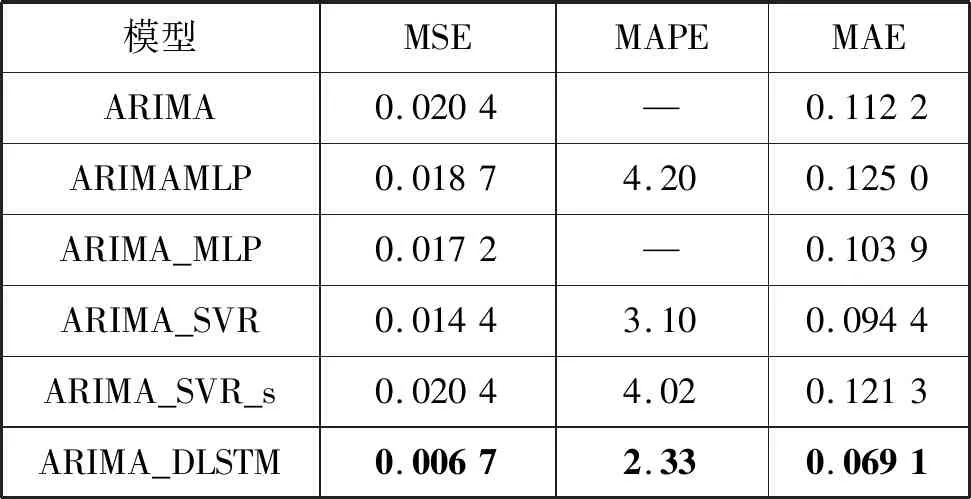
表2 对Canadian Lynx时间序列预测结果

图6给出ARIMA模型和ARIMA_DLSTM模型在Canadian Lynx测试集上的预测结果。由图6可知，ARIMA_DLSTM模型的预测结果和真实值更加接近，有效提高了ARIMA模型的性能。

图6 ARIMA模型和ARIMA_DLSTM模型在Canadian Lynx的时序列测结果

(2) Colorado River flow数据集。在SVR模型中，惩罚系数C为1 000，不敏感损失系数ε为0.001，宽度系数γ为0.01，时间步(输入序列长度)为24。LSTM模型的每层神经元个数分别为24和34，dropout为[0.14,0.32,0.22,0.18,0.28,0.18]，时间步为43，迭代次数为2 000次。

图7给出利用贝叶斯优化算法对LSTM模型进行超参数优化的最优验证误差迭代图。可见，算法在第30次迭代后误差值最优。

图7 贝叶斯优化算法在Colorado River flow的验证误差迭代图

表3给出了不同模型在Colorado River flow时间序列测试集中的预测结果。可见，ARIMA_MLP模型的MSE和MAE值在比较模型中最优，ARIMA_SVR_s模型的MAPE值最优，而ARIMA_DLSTM模型的测试结果比最优MSE、MAPE和MAE值分别降低82.15%、41.58%和38.26%。

表3 对Colorado River flow时间序列预测结果

图8给出ARIMA模型和ARIMA_DLSTM模型在Colorado River flow测试集上的预测结果。可以看出，ARIMA_DLSTM模型预测值存在滞后现象，但和真实值更接近，优于ARIMA模型。

图8 ARIMA模型和ARIMA_DLSTM模型在Colorado River flow的时序预测结果

(3) Airline Passengers数据集。在SVR模型中，惩罚系数C为1 000，不敏感损失系数ε为0.01，宽度系数γ为0.01，时间步(输入序列长度)为16。LSTM模型的每层神经元个数分别为35和22，dropout为[0.14,0.27,0.11,0.10,0.27,0.25]，时间步为47，迭代次数为2 000次。

图9给出利用贝叶斯优化算法对LSTM模型进行超参数优化的最优验证误差迭代图。可以看出，算法在第41次迭代后误差值最优。

图9 贝叶斯优化算法在Airline Passengers的验证误差迭代图

表4给出了不同模型在Airline Passengers时间序列测试集中的预测结果。可以看出，ARIMA_SVR_s模型预测结果在比较模型中最优，而ARIMA_DLSTM模型的测试结果比最优MSE、MAPE和MAE值分别降低23.61%、8.09%和5.72%。

表4 对Airline Passengers时间序列预测结果

图10给出ARIMA模型和ARIMA_DLSTM模型在Airline Passengers测试集上的预测结果。可以看出，ARIMA_DLSTM模型预测值和真实值间趋势基本吻合，有效提高了ARIMA模型的预测精度。

图10 ARIMA模型和ARIMA_DLSTM模型在Airline Passengers 时间序列预测结果

(4) 比特币汇率数据集。在SVR模型中，惩罚系数C为1 000，不敏感损失系数ε为0.001，宽度系数γ为0.01，时间步(输入序列长度)为7。LSTM模型的每层神经元个数分别为23和22，dropout为[0.23,0.11,0.17,0.16,0.32,0.16]，时间步为40，迭代次数为2 000次。

图11给出利用贝叶斯优化算法对LSTM模型进行超参数优化的最优验证误差迭代图。可以看出，算法在第16次迭代后误差值最优。

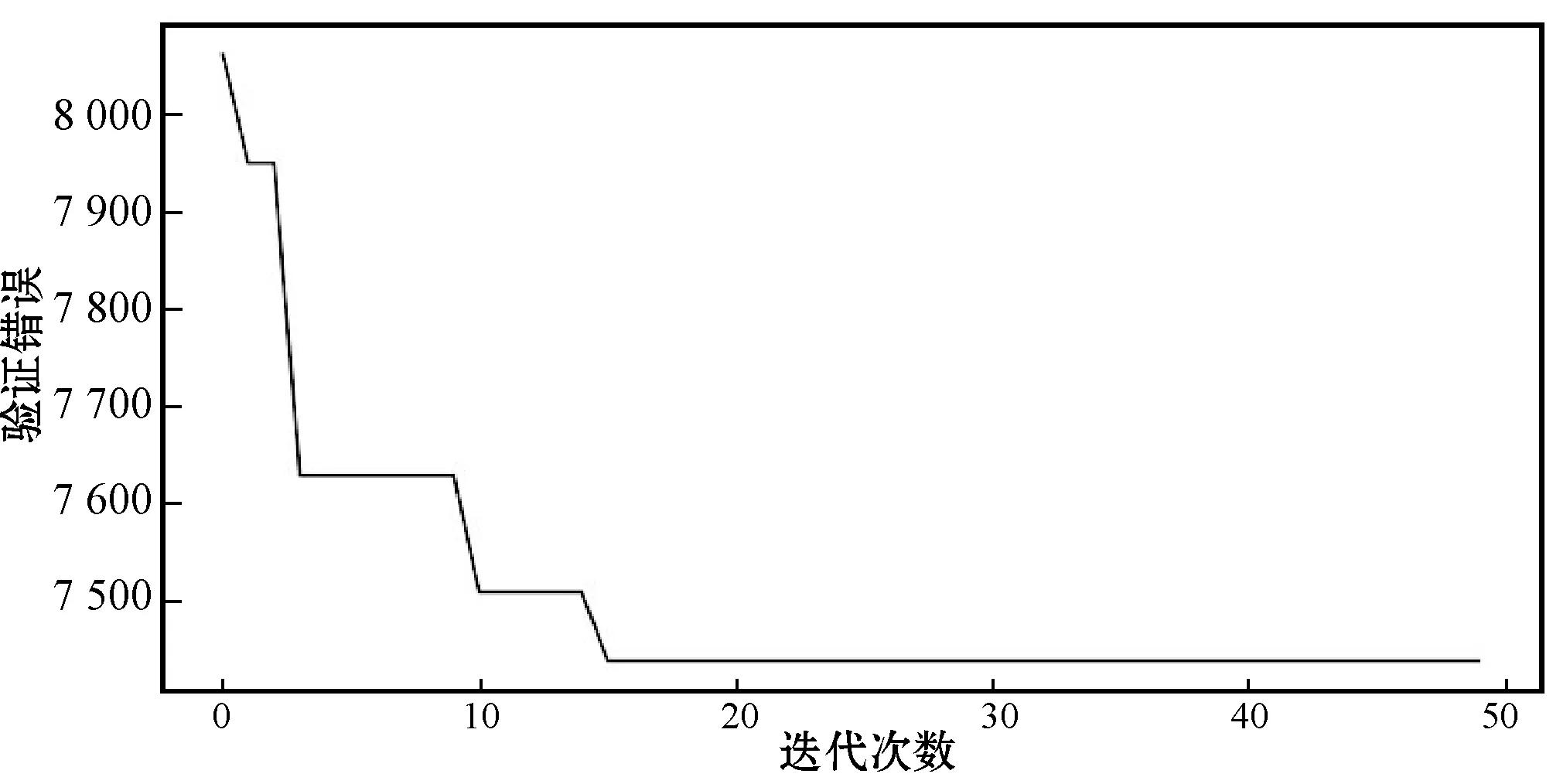
图11 贝叶斯优化算法在Bitcoin汇率的验证误差迭代图

表5给出了不同模型在Bitcoin汇率时间序列测试集中的预测结果。可以看出，ARIMA_SVR_s模型预测结果在比较模型中最优，而ARIMA_DLSTM模型的测试结果比最优MSE、MAPE和MAE值分别降低17.8%、17.13%和10.4%。

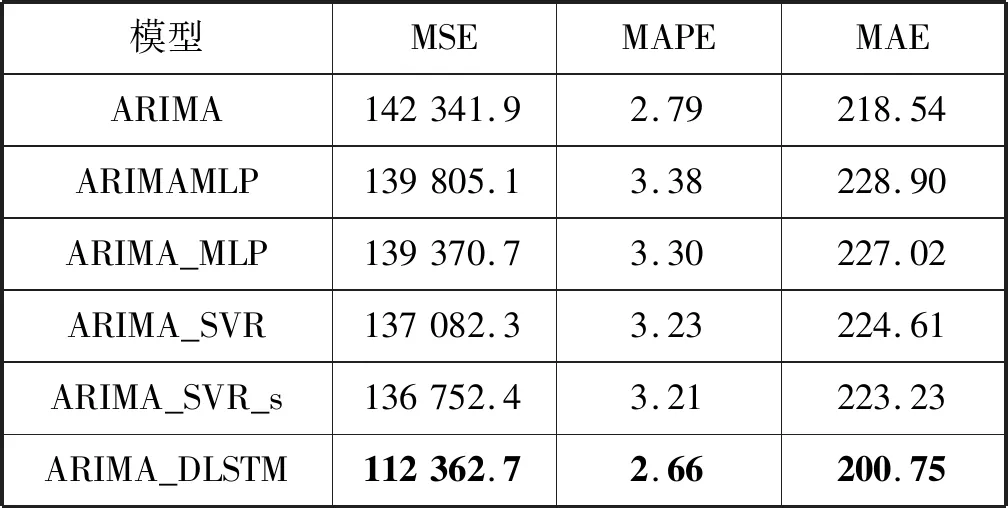
表5 对Bitcoin汇率时间序列预测结果

图12给出ARIMA模型和ARIMA_DLSTM模型在Bitcoin汇率测试集上后20组数据的预测结果。可以看出，ARIMA_DLSTM模型预测值和真实值之间虽有滞后现象，但趋势吻合，能够提高ARIMA模型的预测精度。

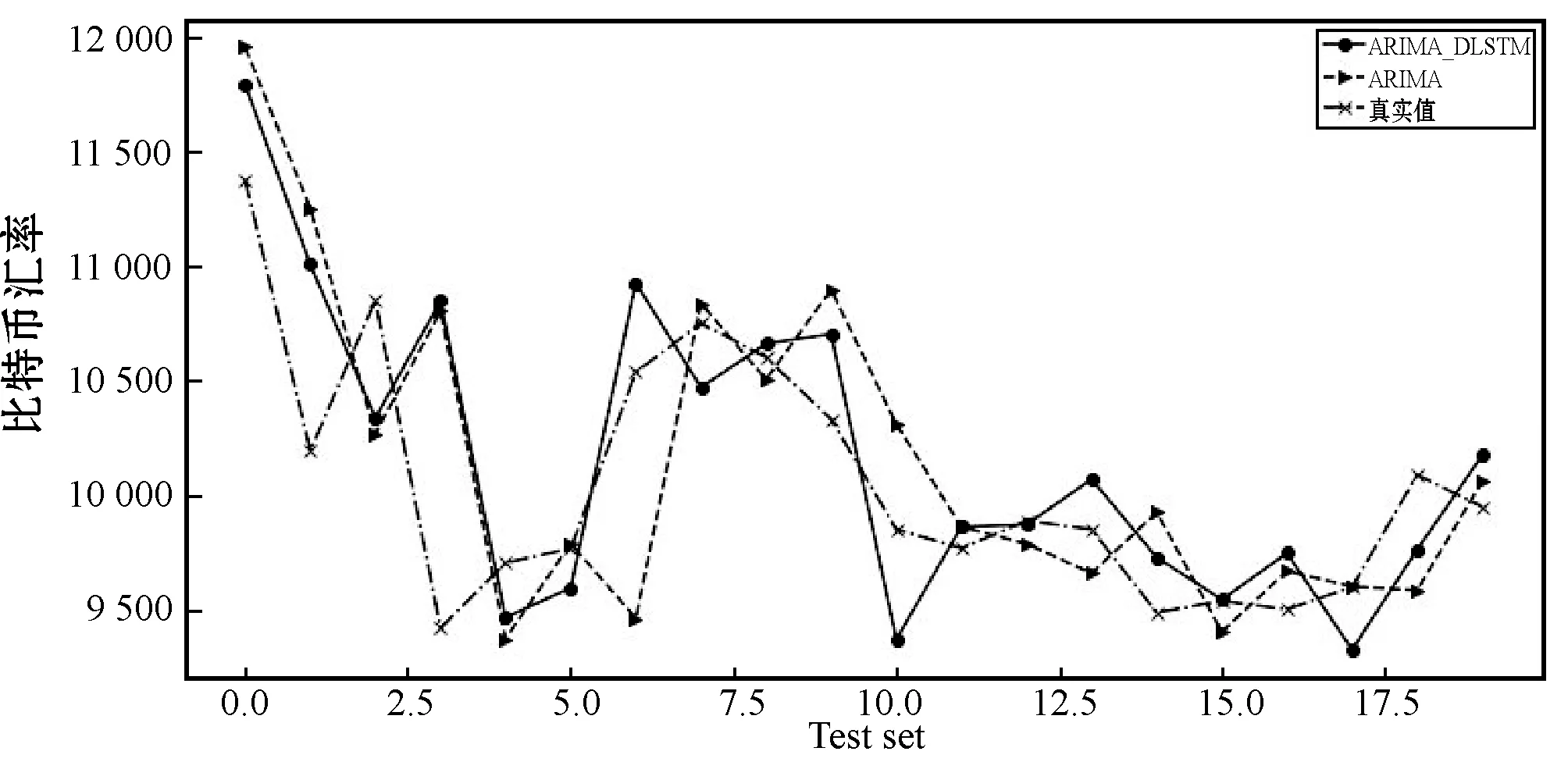
图12 ARIMA模型和ARIMA_DLSTM模型在Bitcoin汇率时间序列预测结果

(5) 糖价格指数数据集。在SVR模型中，惩罚系数C为1 000，不敏感损失系数ε为0.001，宽度系数γ为1，时间步(输入序列长度)为3。LSTM模型的每层神经元个数分别为27和5，dropout为[0.03,0.18,0.19,0.06,0.01,0.3]，时间步为20，迭代次数为2 000次。

图13给出利用贝叶斯优化算法对LSTM模型进行超参数优化的最优验证误差迭代图。可以看出，算法在第25次迭代后误差值最优。

图13 贝叶斯优化算法在糖价格指数的验证误差迭代图

表6给出了不同模型在糖价格指数时间序列测试集中的预测结果。可以看出，ARIMA_SVR_s模型预测结果在比较模型中最优，而ARIMA_DLSTM模型的测试结果比最优MSE、MAPE和MAE值分别降低12.48%、3.17%和3.88%。

表6 对糖价格指数时间序列预测结果

图14给出ARIMA模型和ARIMA_DLSTM模型在糖价格指数测试集上后20组数据的预测结果。可以看出，ARIMA_DLSTM模型预测值和真实值更接近，精度更高。

图14 ARIMA模型和ARIMA_DLSTM模型在该时间序列预测结果

图15给出了5个数据集下的ARIMA模型和5种混合模型的MSE误差比雷达图，图中曲线的顶点位置越靠近边缘则显示MSE误差比越大，说明相应的混合模型相比于ARIMA模型的MSE误差更低。可以看出，ARIMA_DLSTM模型在所有时间序列中MSE误差最低，其中在Colorado River flow时间序列中的误差比最大，优势最为明显。

图15 5个数据集下的MSE误差比雷达图

8 结 语

本文提出了一种基于ARIMA模型、SVR模型和深度LSTM模型的ARIMA_DLSTM时间序列混合预测模型。ARIMA模型和SVR模型能够分别提取时间序列的线性特征和误差序列的非线性特征，深度LSTM模型对线性和非线性预测结果进行非线性组合。对来自不同领域的时间序列进行实证分析，实验结果表明，提出的ARIMA_DLSTM模型和其他混合模型相比，能够有效提高预测精度，有一定的实际应用价值。