基于稀疏子集分析的轨迹聚类发现*

薛 璇 陈平华

（广东工业大学计算机学院 广州 510006）

1 引言

随着现如今人们在社区间的轨迹日渐增多，通过轨迹来检测社区对于社会行为分析和推荐服务都成为关注热点，所以对检测社区的精确度要求越来越高。现有的研究侧重于社会联系和图分区中的社区检测，但在实践中，由于隐私问题，现实生活中的生活联系很难被捕捉。不过，我们可以利用Wi-Fi 和 GPS 设备捕捉人类行为轨迹［1～2］。为了更好地检测轨迹中可能存在的社区，对检测的精确度要求越来越高。一般地，社区检测通常通过聚类来实现，轨迹聚类的目的是从一组运动物体的轨迹中识别聚类，其中特定聚类中的轨迹在一个或多个运动相关特征中表现出相似性［3］。轨迹数据的示例包括车辆位置数据，动物移动数据和人类行为跟踪数据。 因此，对于轨迹数据集执行数据挖掘和行为分析的研究越来越受欢迎［4］。

现有研究通过将共享位置视为社区关系的唯一决定因素，可能错过真实关系或者可能错误地识别不存在的社区。在社交图社区检测文献［5］中，社区通常定义在基于链接的图上，捕获直接的成对交互；由于隐私问题或技术限制，这种明确的交互标记显然难以在许多实际环境中直接获得。Zhou等［1］对物理世界中的三种人类行为轨迹集进行分析，提出基于轨迹多源扩散模型社区检测（Trajectory-based community detection by diffusion modeling on multiple information sources，TODMIS）算法，通过对轨迹数据集四个维度（语义、空间、时间、速度）的建模，将附加信息与原始轨迹数据相结合，并在多个相似性度量上构建扩散过程，在耦合的多图上发现不同社区的集合（包括社区大小），并使用不同的真实数据集进行评估，实验结果证明了该方法的有效性。

2 相关工作

TODMIS［2］使用稠密子图检测方法来检测社区，该方法表示一个概率聚类的顶点集合，它是标准单形空间中的单位向量，然后引入二次函数来测量它们之间的平均边缘权重，并且显性集被定义为具有最大平均边缘权重的子图，其中图中顶点表示轨迹，顶点间的权重代表轨迹间的相似度。目标是对顶点集进行迭代，每一次都能处理检测到一个具有最大平均边缘权重的子图，该子图就是所要获取的社区。然后删除已经构建子图的顶点，再次优化过程，直至顶点集为空。

对于社区检测的聚类问题，TODMIS 算法只在每次迭代中检测现有轨迹集中最大相关性的轨迹集，并没有考虑到迭代过程中可能存在的多个相关性较大的轨迹集，忽略最大相关性轨迹集与其他轨迹集的关系，从而陷入局部最优。其次，在每次迭代过程中，一些与社区相关性较大的轨迹被当作为异常值处理而被忽略，从而降低了社区检测的精确度。因此选择合适的方法对提高轨迹集聚类分析和社区检测至关重要。

为了克服现有技术的缺点与不足，提高轨迹数据集聚类精确度，解决算法鲁棒性和全局最优等问题，本文提供一种基于稀疏子集聚类分析的社区检测方法，这可以避免陷入局部最优，在确定轨迹集的情况下，无需进行算法迭代和多次计算，提高检测社区的效率。

3 基于稀疏子集分析的聚类算法

给定一轨迹集，我们的目标是发现轨迹集中存在具有相似性的轨迹组，定义为表示集或样例。当在空间的度量下进行评估时，某个社区的轨迹表现出类似的行为。算法框架如图1。

首先，对轨迹数据集进行预处理，构建轨迹相似度矩阵，由空间关系特征矩阵定义。通过全局对齐核（GAK-IP）［6］来测量两个轨迹之间的空间相似度，构建轨迹集的空间关系矩阵。其次，将轨迹相似度矩阵转化成不相似度矩阵，对不相似度矩阵进行稀疏子集选择（DS3）［7］得到多个聚类簇；同时对每个聚类簇设置一个标签，在轨迹数据集上构建图，将标签扩散到所有轨迹。

图1 算法模型框架

3.1 构建特征矩阵

用户的轨迹反映用户的行为特征，用户的移动路线可以用时间序列片段来表示。对于两个用户的轨迹，定义时间序列如下：

xa和xb表示第 ɑ 个用户和第 b 个用户的所有运动轨迹的时间序列表，长度分别为m 和n，xa(1 )表示在第一个时间用户ɑ 所在的经纬度。由于每个用户在相同时间内的轨迹移动长度不同，所以，当m=n时，用户ɑ和b的轨迹相似性度量可以用欧式距离表示，即

当m≠n时，需要采用动态规划法对齐时间序列，运用已有的DTW动态时间归整算法构造一个m×n的矩阵网格S，如图2 所示。矩阵元素d(i，j)表示xa(i)和xb(j)两个点的欧式距离，即序列xa的每一个点和xb的每一个点之间的相似度，距离越小则相似度越高。在矩阵网格S 中寻找一条通过此网格中若干点的路径，路径通过的格点即为两个序列进行计算对齐的点。

图2 网格S

由于用户轨迹长度不同，不能使用欧式距离进行匹配，需要在网格S中找到每个连续的点构成路径，但是必须保证曲线中从初始点d(1 ，1) 开始到终点d(m，n)结束，这是就要找出代价最小的那条路径，定义为R：

其中R的第k个元素定义为rk=(i，j)k，定义了序列xa和xb的映射。

路径不是随意选择的，需要满足两个约束条件：1）任何一条轨迹的移动速度快慢都可能变化，但是其各部分的先后次序不可能改变，因此多选的路径必定经过d(1 ，1) 和d(m，n)两点，在网格S中从左下角出发，到右上角结束。2）如果当前路径节点为Rk-1(i，j)，那对于路径下一个节点Rk(i'，j' )必须满足 0 ≤ (i' -i)≤1 和 0 ≤ (j'-j)≤1，在匹配路径时，当前匹配的节点k-1的下一个节点k必须是k-1节点的相邻节点，并且R 中的节点随着时间单调进行匹配，以此保证xa和xb中每个坐标都在R 中出现，实现路径的完整性。根据约束条件每个节点的路径只有三个方向，当路径已经通过了节点(i，j)，那么下一个通过的节点只可能是(i+ 1，j)，(i，j+1)或(i+ 1，j+1) 。所以匹配两条轨迹代价最小的路径：

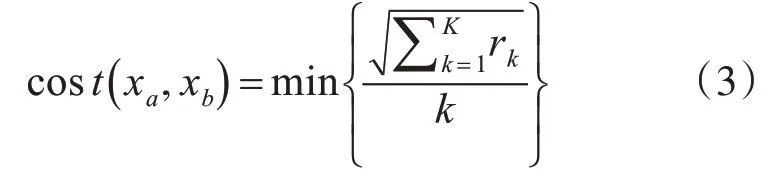
K主要是用来对不同的长度的匹配路径做补偿。

定义一个累加距离c，从网格S中(1 ，1) 点开始匹配这两个序列xa和xb，每经过一个节点，之前所有的节点几点的距离都会累加，到达终点(m，n)后，累积之前经过节点的总距离，即为序列xa和xb的相似度。累积距离c(i，j)为当前节点距离d(i，j)，即点xa(i)和xb(j)的欧式距离与可以到达该点的最小邻近节点的累积距离之和：

所以xa和xb的相似度cab=c(m，n)。

给定N条轨迹，构建N×N相似度矩阵D，

其中d(p，q)表示第p 条轨迹和第q 条轨迹的相似度，即d(p，q)=cpq，d(p，p)=0 表示轨迹 p 与自身最小距离为0。

3.2 稀疏子集分析

从大规模的数据集或模板中找出有信息量、代表性的子集是一个重要的问题。对于数量繁多复杂的轨迹集，给予一对原集和目标集的元素之间的不相似度，从原集中找到一个子集，称为样例或表示，使得其可以有效地描述目标集，运用解决行稀疏约束的迹最小化问题的算法［7］，对特定环境下的轨迹集进行行为分析。

给定一个原集A={a1，a2，...am} 和一个目标集B={b1，b2，...bn} ，分别包含 m 和 n 个数据。构建不相似度矩阵矩阵S，两个数据集之间每一对元素的不相似度{sij} ，每一个{sij} 表示一个ai能表示bj的程度，sij的值越小，ai能越好地表示bj。一般地，相似度{dij} 和不相似度{sij} 可以通过sij=-dij来设置。

给定不相似度矩阵S，目标是选择一个原集A使得可以有效的表示目标集B，定义稀疏矩阵C：M×N，关联不相似度sij，ci是C的第i 行，且ci∈{0 ，1} ，表示ai是否可以表示bj。如果ai是bj的表示，ci=1。为了确保每一个bj能被一个ai表示，必须满足

选择一部分A的元素，根据不相似度，能够很好地编码，运用基于稀疏矩阵的行稀疏约束的迹最小化问题，实现两个目标：1）如果ai被用于表示bj，其表示的代价sijcij∈{0 ，sij} ，则整个原集A表示bj的代价是并且用A编码整个目标集B的代价是；2）当a是目标集B i的某一些元素的表示时，有ci≠0，即C的第i行非零，所以希望使用尽可能少的数据来表示，有较少的表示对应着有较少的非零行在C中。结合以上两种情况，优化问题的目标函数如下：

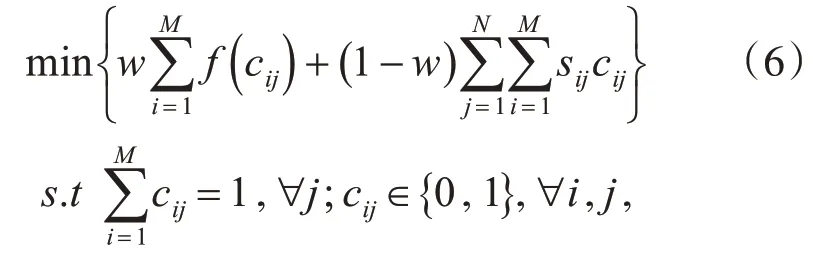
其中f(·) 表示一个指示函数，如果其参数为0，其值为0；否则，值为1。目标函数的第一项对应表示的数量，第二项表示编码目标集B的总代价。约束参数w＞0 权衡两项的大小，对于小的w值，优化时更关注原集A能更好的编码目标集B，能获得更多的表示的数量。在极限的情况下w趋近于0时，目标集B中的每一个元素都由其对应的原集A中的距离最近元素表示，即其中另一方面，如果w的值过大，优化时更关注于矩阵C的行稀疏性，选择数量较少的表示，对于一个充分大的w，目标集B只从原集A中选择一个元素来表达。考虑到另一种情况，当原集A和目标集B相同的情况下，即A=B，当约束参数变得足够小的时候，每一个数据点都由其自身来表示，即当sjj＜sij对任意的j和i≠j时，cii=1。

3.3 轨迹聚类

目标函数的最优解C*不仅表示原集A中的元素被选择用做表示，也包含了目标集B中的元素的表示成员信息表，即

对应着概率向量Bj被原集A中的每一个元素表示，用优化的最终解得到了目标集B的聚类。定义集合{Aℓ1，Aℓ2， ...，AℓT}代表一个原集表示目标集，可以赋予Bj被Aδj表示，根据如下公式

可将目标集B分开至T个组，对应T个表示。

4 实验结果分析

4.1 实验数据

在实验中，选取的数据集来自于微软T-Drive项目［18～19］，T-Drive轨迹数据集包含2008年2月2日至 2 月 8 日期间北京内 10，357 辆出租车的 GPS 轨迹。该数据集包含了1500 万个坐标点，轨迹的总距离达到900多万公里。

为了降低数据的复杂性，本文选取在2008年2月2日至2008年2月8日一周内的每天相同时间片段几组不同的100 个出租车司机移动的轨迹，并且原始的数据集数据表达是经度纬度，为了方便计算，将经纬度映射到二维坐标上，横轴为经度，纵轴为纬度。在时间片段相同的情况下，计算轨迹之间的相似性更为准确。

4.2 实验结果与分析

由于实验是在一个原集上聚类，即目标集是当前原集，选取约束参数w两组不同的值（0.2，0.8）对100 组轨迹集进行稀疏子集分析，比较原集在约束参数不同的情况下，生成表示或样例的个数。实验结果如图3和图4所示。

如图3所示，当w=0.2时，100个轨迹集中有聚类中心T有6 个，分别是{1 2，32，54，66，85，90} ，图中颜色越深代表此聚簇所包含的信息量越重要，原集中的元素越能很好的表示目标集。

如图4 所示，当w=0.8 时，数据集中的聚类中心T只有3 个，分别是{9 ，32，71} ，当w越大时，原集中可以表示目标集的元素越来越少，可用来表示的信息量数量较少。

图3 约束参数w=0.2 聚类结果

图4 约束参数w=0.8 聚类结果

综上所述，在稀疏子集聚类时，需要找到合适的约束参数进行对比，从原集中找出能表示重要信息的样例来表示目标集。本文算法在保持数据集的完整性的前提下对轨迹数据进行了有效的聚类分析，得到原集中有信息量的样例。

5 结语

本文针对现实环境下的出租车轨迹进行数分析和聚类，研究相同时间片段内一个城市中出租车移动的轨迹特征，运用稀疏子集分析密集复杂的数据集，充分利用原集自身表示的特点，降低计算的复杂度，提高聚类检测的效率。

但是，我们的工作还存在一些需要改进的地方，比如考虑多个维度的特征向量来更精确地表示数据集，将实验运用到不同环境下的物理轨迹数据集，因为出租车行驶轨迹比较密集和复杂，路线的规划一般由运营公司规划，缺少灵活性，增加原集与目标集的对比和表示，提高稀疏子集分析的正确率。