基于SVD++与改进Slope One 混合推荐算法研究*

叶 飞 边 琳 杨林楠

（1.云南农业大学大数据学院云南省高校农业信息技术重点实验室 昆明 650201）（2.云南农业大学水利学院云南省高校农业遥感与精准农业工程研究中心 昆明 650201）

1 引言

近年来，随着互联网规模的扩大，信息技术与应用的快速发展，如何从过载的信息中筛选用户喜好和兴趣数据成为了影视、音乐、新闻、书籍、电商平台亟待解决的难题。基于协同过滤算法的个性化推荐技术具有高效性、简单性、准确性特点，协同过滤算法是当前个性化推荐系统应用中效果做好的推荐算法［1］。推荐系统在应用过程中，由于大部分用户仅对部分项目进行评分，导致评分矩阵十分稀疏［2］，推荐算法的准确度较低。为解决数据稀疏性问题，SVD 算法［3］（Singular Value Decomposition，奇异值分解）用于解决用户-项目矩阵中的数据稀疏性问题，通过将高维的稀疏评分矩阵降维，挖掘矩阵中特征值，补全矩阵中的缺失值，用预测值对未评分项目进行填充。SVD++［4］算法将用户的历史评分行为矩阵加入到SVD算法中，提高了算法的准确度。在SVD++算法对稀疏的评分矩阵进行填充后，再通过改进的 Slope One［5～6］算法对缺失值进行二次预测，再次提高预测的准确度。

因此，本文提出SVD++算法和融合项目相似度Slope One 算法结合的混合推荐算法通过调整预测评分，从而进一步提高推荐的准确度。实验结果表明，与原始的Slope One算法和SVD 算法相比，混合算法的推荐误差较小。

2 相关工作

协同过滤（Collaborative filtering）［7］推荐算法是目前学者们研究较多的推荐算法之一，协同过滤分为两类，一类为基于内存的协同过滤另一类为基于模型的协同过滤。基于内存的协同过滤需要在内存中存储较大的相似度矩阵，经过算法处理提供推荐。它包含基于项目（item-based collaborative filtering，IBCF）和基于用户（user-based collaborative filtering，UBCF）。基于模型［8］的协同过滤及为机器学习和数据挖掘的模型，它包括极大熵模型、马尔科夫模型、概率相关模型、关联规则模型、回归模型、贝叶斯网络模型和奇异值分解（SVD）聚类模型。协同过滤算法的原理是通过计算“用户-项目”评分矩阵相似度对目标用户做推荐。

3 SVD++算法

3.1 SVD算法

SVD 可以将高维用户项目评分矩阵通过奇异值分解降维成低维用户、项目的特征向量矩阵，它是线性代数中的矩阵分解方法。用SVD 方法对评分矩阵进行分解，通过奇异值挖掘潜在语义特征值进行推荐。传统的SVD算法［9］将评分矩阵分解为3个低维矩阵，为

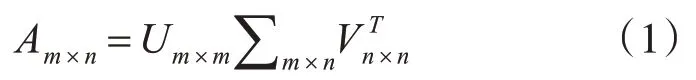
式（1）中，A 为m×n 的原始评分矩阵，U 为m×m 的正交矩阵；V 为 n×n 的正交矩阵；Σ为 m×n 的对角矩阵。该公式表示矩阵A 的向量从V 按照Σ在各方向上的A的奇异值倍数进行伸缩旋转到U。

根据推荐系统的预测评分的实际需求，对式（1）进行简化：

根据式（2）、（3）可以将矩阵A转换为

根据用户项目的评分数据集可以构建评分矩阵R，其中矩阵中的行为用户，列为项目，矩阵中的值代表评分值。将评分矩阵R进行奇异值分解，为

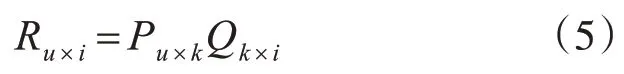
式（5）中u 表示用户数量，i 代表项目数量，k 代表选取的隐形特征值数。SVD 算法通过矩阵R中过已有数据对P、Q矩阵进行训练，然后使用训练好的p、q矩阵对R矩阵进行拟合从而实现对未评分项进行评分预测，计算公式为

式（6）中表示矩阵P的某一行数据，qi表示矩阵Q的某一列数据，r^ui表示用户u 对项目i的评分预测。

在实际模型中，用户评分和商品得到的评分标准各不相同，用户、项目各自本身包含特有属性［10］。引入参数u表示在训练集中所有已有评分数据平均数；参数bu表示用户特有属性，意义为特殊用户的评分习惯与项目本身关联性较小。综合以上实际背景，对SVD公式进行改进为以下形式：

3.2 SVD++算法

为进一步优化评分预测的准确度，SVD模型将用户的历史行为记录扩展到用户的特征矩阵中，构建成为 SVD++［11］模型。

根据项目的协同过滤算法（IBCF）［12］关于用户历史行为数据对评分预测的计算公式：

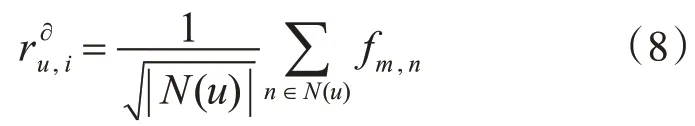
式（8）中N(u)表示用户u 的历史行为数据，它包含用户评分项目和历史浏览记录的项目集。N(u)的次方是一个经验值。fm，n表示项目间的相似度矩阵，它可以分解成向量积的形式，即因此公式可以转化为

将历史用户行为记录模型和SVD模型相结合，从而得到SVD++模型，该模型表示为

为避免参数对SVD++模型的过拟合，可以将式（9）进行qi对xi的置换处理，经过整合式（10）可得：

3.3 SVD++算法描述

本文采用随机梯度下降算法更新SVD++模型中相关参数，随机梯度下降法通用的表达

式为：y(x+1)←y(x)+∂*h(x) ，其中 ∂ 为学习速率，可以是较小的常数，也可以是一个函数表达式；h(x)是y(x)的梯度；x为迭代次数。为保留原始评分矩阵数据的真实性设定奇异阙值γ［13］，通常γ值取成0.99。

SVD++算法

输入：训练数据集R′，测试数据集R″，阈值γ，迭代次数n，学习速率∂，隐特征数k，正则化系数λ。

输出：预测填充结果数据集。

1）初始化特征矩阵P和Q，使向量pu，qi的值为random(0，1)/sqrt(k)，并把偏置项bu，bi和向量yj中的值初始化为0。

2）根 据 预 测 评 分和 实 际 评 分ru，i通 过 公 式计算误差值。

3）梯度下降法的最小化损失函数为

式（12）中前半部分表示部分，后半部分表示防止训练出现过拟合的正则化部分。最小化损失函数通过对特征变量bu，bi，pu，qi和yj求偏导，得到特征变量的梯度向量，沿着梯度方向更新特征变量，直到梯度向量趋向于零。特征变量的迭代更新公式为

通过更新得到上述特征参数，执行步骤2）判断误差eu，i是否小于阈值γ，若小于γ则停止训练，否则跳到步骤2）。

通过训练得到的参数，对测试数据集R″中未评分项进行预测评分，然后进行填充，输出填充预测结果的评分矩阵。

通过重复大量实验调整参数n，∂，k，λ使得算法最优，SVD++预测的精准度达到最高。

4 相似度算法

本文采用项目相似度，常用的相似度算法为欧式距离相似度、余弦相似度、修正余弦相似度［14］、Pearson相似度［15］和Jaccard相似度。SVD++算法对评分矩阵做了初步的数据填充，数据稀疏性大大降低，采用修正余弦相似度和Pearson 相似度的权重计算融合相似度，该融合相似度的值即为改进Slope One算法中的权值。

4.1 修正余弦相似度

余弦相似度通过改进用户没有考虑评分尺度问题，计算相似度时减去用户对项目的平均评分，从而达到去中心化的目的。

式（14）中ru，i，ru，j分别表示用户u对项目i，j的评分，分别表示所有用户对项目i，j评分的平均值。

4.2 Pearson相似度

Pearson 相似度是基于Pearson 相关系数计算项目间的相似度，Pearson 相关系数反映变量间的线性相关性程度，当两个变量线性关系增强时相关系数趋向于1 或者-1。Pearson 相关系数大于0 时变量正相关，小于0时负相关。

式（15）中ru，i，ru，j分别表示用户u对项目i，j的评分，表示同时对项目i和j都评分的用户集合Ui，j对项目i的评分平均值，表示同时对项目i和j都评分的用户集合Ui，j对项目j的平均值。

4.3 融合相似度

针对上述提到的修正余弦相似度和Pearson 相似度可以通过引入权重的方式进行融合，计算出最终的项目相似度。

θ的取值范围为［0，1］，调整θ参数即为设置相似度的权重，通过测试数据集试验选取适当的值，使得提高推荐的准确度。

5 改进Slope One算法

Slope One 算法是一种基于线性回归的项目评分的算法，应用公式f(x)=x+b来预测评分，x表示评分值，b为项目间的评分偏差。计算项目i和j之间的偏差公式为

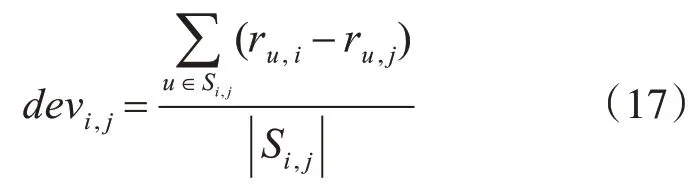
ru，i，ru，j表示用户u对项目i，j的评分，Si，j表示同时对项目i，j评分的用户集合，| |Si，j表示集合Si，j中用户数。

根据偏差式（17）可以转化为用户u对项目i的评分预测公式为

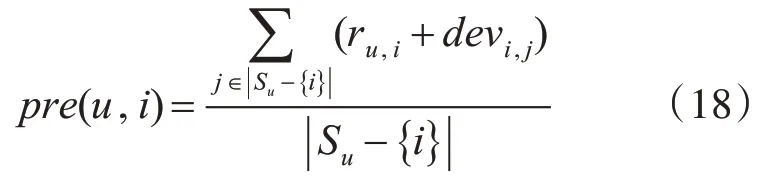
S(u)表示用户u评分的项目集合，S(u)-{i} 表示用户u与项目i同时评分的项目集合。

加权Slope One 算法［16］对评分矩阵中缺失值进行二次预测，进一步提升推荐的准确性，计算得到最终的评分矩阵。进行Slope One 算法改进时使用的评分矩阵为填充完整的评分矩阵，Si，j就是完整的用户集U。将融合相似度sim(i，j)加入到Slope One算法中，得到改进Slope One公式为

本文S(u)-{i} 集合选取相似度邻近集合中N个最大的项目集合。

改进Slope One算法

输出：预测评分pre(u，i)和最终填充矩阵Ri，j。

1）设定大小合适的w组成S(u)-{i} 项目集合；

3）根据式（19）使用相似度邻近集合最大值集合S(u)-{i} 、项目相似矩阵Kn，n中项目相似度值和项目偏差值deνi，j求得pre(u，i)；

4）输出pre(u，i)，并使用pre(u，i)更新评分矩阵，输出最终评分矩阵Ri，j。

6 实验与结果分析

6.1 实验数据

实验数据采用美国Minnesota大学公开的MovieLens数据集，本文选用100K 数据集包含943个用户，1682 个项目，100000 条评分记录，数据稀疏度为0.937。实验过程中为避免随机性对实验结果产生影响采用五折交叉法，80%的评分数据集作为训练集，另外20%的评分数据集作为测试集。

6.2 评价指标

实验使用均方根误差（Root Mean Squared Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）作为预测评分精准度评价指标。

1）平均绝对误差（Mean Absolute Error，MAE）

MAE 用来衡量所有用户对于项目的预测值和真实值差的平均值，MAE 值越小，预测精度就越高。

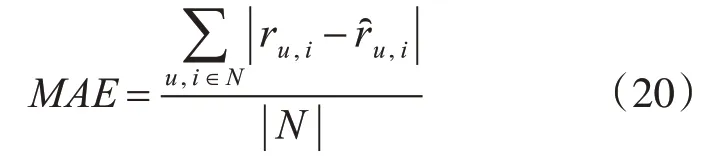
式（20）中，ru，i表示用户u对项目i的实际评分，表示用户u对项目i的预测评分，N表示项目集，|N|表示项目集的大小。

2）均 方 根 误 差（Root Mean Squared Error，RMSE）

RMSE 作为预测值精准度的评价指标，RMSE值越小，预测值精准度越高。

6.3 结果与分析

6.3.1 SVD++模型中训练迭代次数实验

通过实验研究SVD++模型中训练迭代次数n的大小对评分矩阵预测准确率的影响，实验结果如图1所示。

图1 不同训练迭代次数下RMSE的值

图中横坐标为训练的迭代次数，纵坐标为RMSE 的值。分析本图发现训练迭代次数在25 时趋向稳定，所以本文SVD++模型训练迭代次数n 选用25。

6.3.2 SVD++模型中隐形特征数实验

本文实验研究SVD++模型中隐形特征数k 的大小对评分矩阵预测准确率的影响，并确定效果最好的隐形特征数。实验结果如图2所示。

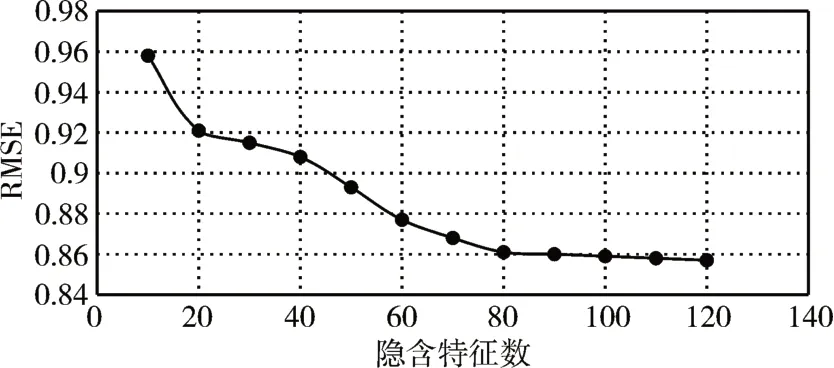
图2 不同隐形特征数下RMSE的值

图中横坐标为隐含特征数，纵坐标为RMSE 的值。分析发现隐形特征数在80 时趋向稳定，所以本文SVD++模型隐形特征值k选用80。

6.3.3 相关算法对比试验

为验证SVD++与改进Slope One 混合算法的精准性，本文选取SVD Slope One算法、加权Slope One算法两组组模型进行对比，分别测试评分矩阵测试集的MAE 的值。考虑到项目的相似度邻近集合最大值W对推荐精准度的影响，本文将三组模型结合邻近集合最大值W进行实验，结果如图3所示。

图3 不同邻近集合最大值W与三种算法MAE值

实验结果表明，本文提出的SVD++与改进Slope One 混合算法模型推荐效果最佳，MAE 值最小。邻近集合最大值W 在到100时，MAE值趋向稳定，推荐效果较好。SVD++与改进Slope One 混合算法较SVD Slope One 算法、加权Slope One 算法的MAE值提升了2.89%和6.87%。

7 结语

本文针对传统协同过滤算法存在评分矩阵数据稀疏性问题提出SVD++算法对缺失评分数据进行预测评分并进行填充，针对稀疏矩阵填补空值过于单一提出在初步填充后使用改进Slope One 算法进行二次预测，项目间的相似度计算本文提出融合相似度方法，提高推荐的精准度。下一步研究的方向为解决冷启动问题和有效地减少算法计算时间以及有效节约系统计算资源。