存在视觉盲区的小型无人机群自主控制*

赵 虎 李晓丽 尹德斌

（1.东华大学信息科学与技术学院 上海 201620）（2.数字化纺织服装技术教育部工程研究中心 上海 201620）（3.上海工业自动化仪表研究院有限公司 上海 200030）

1 引言

近几年来，无人机研究越来越引起国内外专家学者的关注，特别是对无人机的编队控制的研究受到许多学者的青睐。随着战场环境的多变性和复杂性，单架无人机已经无法满足现实的需求。为此，许多专家提出利用多无人机以协同的形式进行编队飞行来执行任务。就目前来说，对于无人机的编队飞行，前人已经提出了很多的方法，比如长机-僚机法，行为法，虚拟结构法，基于一致性的编队控制方法，人工势场法等；施书成［1］等根据长机-僚机方法设计了多无人机编队协同保持的速度矢量场算法，并借鉴人工势场的方法，引入相对速度矢量，从而保证了无人机群以相对稳定的速度进行飞行，并且具有防碰撞功能。周子为等［2］根据雁群的行为机制，提出了一种编队重构拓扑方法。该方法能够使得无人机紧密编队，并且可以大大地减少无人机的耗油量。刘成功［3］等对无人机仿生紧密编队飞行控制技术进行了研究，分析了候鸟编队飞行原理，讨论了无人机紧密编队飞行的仿生机理，建立气动耦合效应的紧密编队飞行模型，并设计了基于小脑模型神经网络与PID 复合控制的队形保持控制器，通过仿真实验结果表明所设计控制器的合理性。郭冬冬［4］等运用二阶一致性的方法，通过对无人机协同编队方法的研究，设计了二阶有领航者的一致性控制算法，以及基于人工势场法设计了群体控制算法，通过实验验证，该算法可以让多个无人机跟随领航者保持一定的队形飞行。张佳龙［5］等人对基于改进人工势场的无人机编队避障控制研究，对人工势场法在无人机避障过程中存在的局部最小值问题，利用了虚拟结构和长机-僚机控制控制策略，提出了一种三维空间复合矢量人工势场方法，从而实现了无人机编队飞行过程中能够在三维空间避开障碍物的目的。除此之外，Lin，ZJ 等［6］通过对小型无人的研究，根据火灾任务的需求，通过分布式编队的方式，提出了一种基于一致性的无人机群合作方法，最后经过仿真验证了该算法可以将无人机分组覆盖到火线轮廓的不同部分，从而提高了救灾效率。Feng 等［7］提出了一种基于一致性的均匀无人机群鲁棒聚类和优化算法。该算法可以实现无人机群的自适应地集群并可以自适应的选择一架无人机作为领航者。 林敏等［8］针对多智能体的时变问题，设计了一致性算法和具有避障功能的人工势场法，从而使得僚机能够跟随长机稳定飞行。

论文的研究借鉴了雁群飞行编队的行为。在雁群进行编队飞行的过程中，大雁由于其生物体本身的特性，存在一定的视觉盲区。为此，本文根据这一问题，提出了一种基于视觉盲区的小型无人机自主控制算法，首先是构建了二阶积分器系统模型，通过对无人机在视觉盲区和非视觉盲区的区别，设计代价函数进行刻画视觉盲区和非视觉盲区，然后利用了梯度下降法以及以图论作为理论基础的速度一致性算法使无人机在避开彼此视觉盲区的基础之上速度达到一致性，通过仿真实验，最后验证了所设计的控制器的合理性。

2 无人机编队飞行的运动学分析

假设无人机现在飞行到O 点，此时无人机的俯仰角为βi，偏航角为θi，无人机的飞行速度为Vi。如图1 所示建立无人机的地面坐标系，根据文献［9］对于小型固定翼无人机的非线性动力学方程为

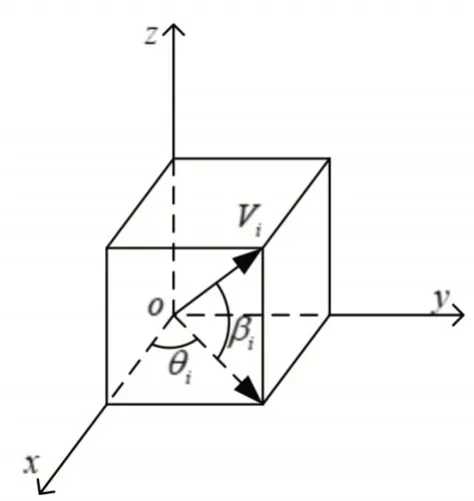
图1 小型固定翼无人机飞行运动学模型

其中：Vi为无人机对地的飞行速度ai=[ai1，ai2，ai3]为无人机的加速度，ai1为无人机的切向加速度，其方向与无人机的速度方向一致，ai2为无人机的法向加速度的垂直分量，ai3为无人机的法向加速的水平分量，βi为无人机飞行时的俯仰角，θi为无人机飞行时的偏航角。如果令pi为无人机在某时刻的速度信息，qi为无人机在某时刻的位置信息，则：

然后让式（2）再对时间求导可得：

则式（3）可以表示为ui=k+Aiai，进而可以得到从变换中可以看出，可以将控制输入ai=[ai1，ai2，ai3] 转化为ui，从而可以令ui为新的控制输入，设uix为无人机在x 方向上的加速度，uiy为无人机在y 方向上的加速度，uiz为无人机在z方向上的加速度，则新的控制器输入可以表示为

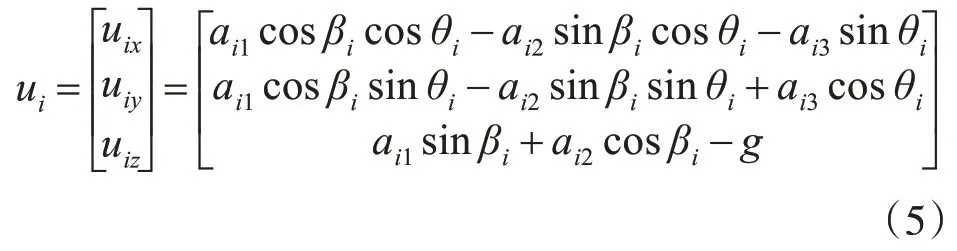
则由此可以将系统状态方程转化为

上式中qi为第i个无人机的位置，pi为第i个无人机的速度，ui为无人机编队时需要设计的新的控制输入。在本文中，假设无人机群是在一个二位平面进行飞行，此时令俯仰角βi=0，z方向的控制输入为零。

3 基础理论

无人机群在编队飞行过程中的通信问题可以用通信拓扑图来描述，在一定的拓扑条件下，每个无人机都可以看成是图中的一个节点，而图中的边可以看成是无人机之间的通信信息流。

假设G=(V，E)为无人机组成的网络图，其中V=[ν1，ν2，ν3，…，νn] 为 图 中 的 节 点N={1 ，2，3，…，n} 为节点的序号，在实际中表示每架 无 人 机 ，E=(e1，e2，e3，…，en) 为 图 中 的 边 集E⊆V*V。M={1 ，2，3，…，n} 为图中边的序号，在实际中代表无人机在相互通信时的信息传递。若信 息 交 换 是 没 有 方 向 性 的 ，则 有 (νi，νj)∈E⇔(νj，νi)∈E，那么此时图 G 被称为无向图；若信息流只能从其中一个节点传递到另一个节点，反之不能传递，则此时称图G 为有向图。此外，邻接矩阵A=[aij] 为非负加权矩阵，当无人机νi有信息向无人机νj传递时，aij＞0（本论文中规定当无人机νi有信息向νj传递时，aij=1），当无人机之间无信息传递时aij=0，所以此时A是由0-1 元素组成的一个非负加权矩阵。对于一个无向图中的节点i，邻接元素可以表示为Ni={νj∈ν|(νi，νj)⊂E}。假设图的出度矩阵为D，易知矩阵D为斜对角矩阵，则此时该图的拉普拉斯矩阵可以表示为L=D-A。

4 控制器的设计

4.1 代价函数的设计

在生物种群中，比如鱼群的聚集，大雁的迁徙，都会按照一定的队形进行排列，比如，大雁的迁徙，就会按照一定的人字形进行编排飞行，这样在迁徙过程中大雁之间不仅会节省自身能量，而且也会方便领航者的交换和使每个大雁都能够在各自的视觉之内飞行，这样就方便了各自之间信息的传递。科学家根据这一生物学行为，将此场景应用到无人机的编队飞行过程中。本文就是根据雁群在飞行过程中由于存在视觉盲区的特点来进行研究。因为无人机群在执行任务时也会存在盲区，所以需要进行避盲算法的设计。

首先，前面提到，无人机在编队执行任务过程中，由于无人机之间有且仅有视觉上的通信，此时就需要各无人机之间保持在视觉盲区之外飞行，所以，为了刻画视觉盲区和非视觉盲区，就需要设计相应的代价函数函数进行刻画。

如图2 所示，假设有两架型号相同的小型无人机，分别为无人机j和无人机i，此时无人机j在二维平面时的坐标为(xj，yj)，无人机i在二维平面时的坐标维 (xi，yi)，无人机的盲角都为α(α＜ 90°)，偏航角为θj，假设无人机j的机头朝向的反向延长线与两架无人机相对位置偏差的夹角为γij，则此时由文献［12］可以到：

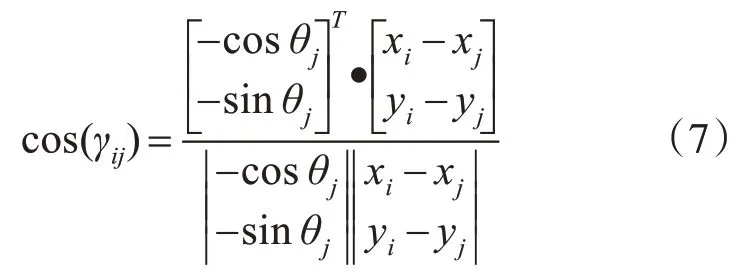
图2 无人机视觉之间的几何关系图

由此可以看出，当 cos(γij)≥cos(α)时，无人机i在无人机j的视觉盲区之内，当 cos(γij)＜ cos(α)时，无人机i在无人机j的视觉盲区之外。由此可以设计代价函数为

当γij∈(0，α]时，函数hcos(γij)与γij的关系如图 3 所示。则从式（8）可以看出，当γij=0 时，hcos(γij) 的值为无穷大，当γij∈(0 ，α]时，hcos(γij)的值从无穷大平滑地过渡到 0；γij＞α时，hcos(γij)的取值为0。然而，对于小型无人机来说，其可视化的距离是有限的，所以为了使无人机能够避免因随时间变化而变化的邻接集Ni(t)所带来的代价函数产生的突变，此时需要定义一个缓冲函数ρ(dij)，此缓冲函数可以使代价函数平滑可微，根据文献［10］可以得到：

图3 代价函数图像

4.2 速度一致性项算法的设计

无人机在编队飞行过程中，除了需要设计代价函数让无人机在盲区之外飞行以外，也需要让无人机保持速度一致性。所以在此就需要速度一致性算法的设计。

如果无人机j在[xj，yj]位置时的速度定义为pj，无人机i在位置 [xi，yi]位置时的速度为pi，则根据文献［13～15］可以得到，要使得无人机群速度保持一致性，则需要满足：

其中，aij是非负加权矩阵中的元素（在本文中aij=1）。这样就可以保证无人机群按照相同的速度大小和相同的速度方向飞行。

4.3 控制器算法

无人机群在飞行过程中，要想飞离其他无人机盲区，就需要使无人机的代价函数为零，另一方面，无人机群在飞行过程中，需要保持速度一致性。根据文献［14］可以得到：

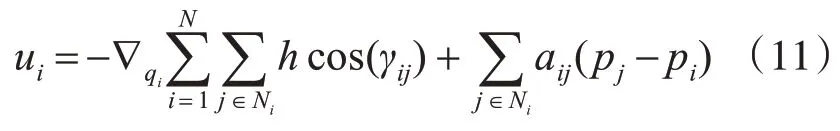
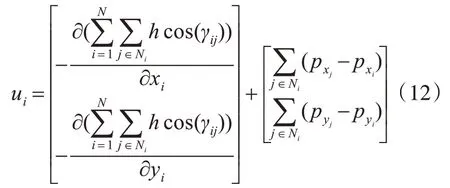
其中，pxi和pyi分别表示无人机i在x方向以及y方向上的速度，pxj和pyj分别表示无人机j在x方向以及y方向上的速度表示无人机i的代价函数在x方向上的负梯度，表示无人机i的代价函数在y方向上的负梯度。下面，通过仿真来验证所设计控制器的合理性。

4.4 仿真结果及分析

根据所提出的算法，进行仿真验证，其中设四架无人机为同一型号无人机，盲角偏转角为指向无人机飞行时的速度方向。

1）当无人机相互不再彼此的盲区之内如表所示。

表1 无人机的初始状态1

图4 无人机初始位置坐标图

仿真结果如图5～7所示。

图5 无人机群的位置坐标

图6 无人机x方向速度与时间的关系

因为无人机群在飞行的过程中，相互不在盲区之内，所以无人机按照初始时的速度和偏转角度直线飞行。

图7 无人机y方向速度与时间的关系

2）当初始状态在盲区之内时如表2。

表2 无人机的初始状态2

图8 无人机初始时刻位置

则无人机飞行的仿真结果如图9～11。

图9 无人机群的位置坐标

通过仿真结果可以得到，当无人机在盲区之内飞行时，无人机之间通过所设计的算法成功避开了视觉盲区继续飞行，并且速度最终达到一致性的效果。

图10 无人机x方向速度与时间的关系

图11 无人机y方向速度与时间的关系

5 结语

本文是基于生物体群体飞行的特征，以小型无人机为研究对象，因小型无人机自身负载小的原因无人机之间只能安装鱼眼镜头作为视觉上的通信，虽然鱼眼镜头可以扩大视野范围，然而仍存在视觉盲区，为解决这一问题，提出了使用代价函数对视觉盲区和非视觉盲区进行刻画，利用二阶积分器模型，根据代价函数的负梯度以及速度一致性得到无人机飞行控制器的实际的输入。 最后通过Matlab仿真，验证所设计控制器的合理性。然而本文只是考虑了使无人机避开盲区以及速度达到一致性，并没有考虑到无人机的编队和避障的需要。这一问题将在以后的研究工作中进行开展。