基于WOA 优化LSTM 神经网络的配电网可靠性评估

万俊杰， 单鸿涛

（上海工程技术大学 电子电气工程学院， 上海 201620）

0 引 言

配电网是电力系统的重要组成部分，其广泛的范围和复杂的结构对可靠性有着重要的影响。 因此，对配电网可靠性进行准确分析即已成为目前的研究热点［1］。

随着工业技术的快速发展，欧美的一些国家开始将配电网可靠性评估列入研究范围。 1964 年，作为一种统计模型，Desineo 等人首次将马尔可夫模型应用到配电网可靠性评估中，此后Billinton 等人［2］对该模型进行深入研究，对马尔可夫模型中转移矩阵组成的线性方程进行求解，最终计算出了系统的平均故障时间以及平均故障修复时间。 上世纪六十年代，加拿大建立了全球报告系统，该系统明确指出要对配电网可靠性的历史数据进行分析，对于不同等级的网架结构需要制定各自的标准［3］。 日本对配电网可靠性的研究有其独特之处，日本对于配电网可靠性各个指标的计算是全国一致的，并将“裕度”这一概念应用于配电网可靠性评估中，以此进行相关研究［4］。 国内的配电网可靠性研究起步于二十世纪七十年代，1985 年，为进行配电网可靠性研究又建立了电力系统可靠性管理中心，并在此基础上开展配电网可靠性研究工作［5］。 继而，在1989年国内又颁布了《供电系统用户供电可靠性统计办法》，自该方法执行以来，配电网可靠性的相关研究工作就得到了迅速发展。

目前常用的配电网可靠性分析方法有3 种，分别是：模拟法、解析法和人工智能方法。 其中，蒙特卡洛法是模拟法中最常见的一种方法。 蒙特卡洛法的计算精度和抽样次数直接相关，只是其计算量大以及计算时间长的特点很难满足在线分析的需求［6］。 解析法一般包括状态枚举法［7］、 故障模式影响分析法［8］及最小路法［9］等。 但是随着网络结构复杂性的增加，使其可靠性分析的难度水平也随之提升，导致计算量大，速度慢的问题。 神经网络算法基于历史样本数据进行分析，其自适应能力强，训练好后可靠性分析时间及计算量有所减少，但计算精度有待提高［10］。 人工神经网络方法的理论主要包括前向递推和反向调节。 文献［11］结合了传统的蒙特卡洛法和人工智能算法，用于配电网可靠性指标的计算，取得了较好的效果。 文献［12］找出影响配电网可靠性的因素，将这些因素作为模型的输入，利用处理线性能力较强的BP 神经网络来研发配电网可靠性评估模型。 文献［13］采用了泛化能力较强的径向基（RBF）神经网络，将配电网可靠性原始数据分为训练集和测试集，对原始数据进行拟合取得了良好的效果。 文献［14］提出一种粒子群优化算法（PSO） 优化最小二乘支持向量机（PSOLSSVM）的配网供电可靠性评估方法。 通过选择影响城市供电可靠性的主要因素作为模型的输入，利用粒子群优化算法（PSO）较强的参数寻优性能对最小二乘支持向量机（LSSVM）的模型参数进行处理得到最优模型，并将该模型应用于实际电网中，证明该方法是可行有效的。 文献［15］提出了一种基于改进的粒子群算法（PSO）优化广义回归神经网络（GRNN）的配电网可靠性预测模型。 先是在基本粒子群算法中引入惯性权重有效地提高了算法的全局和局部搜索能力，然后使用改进的粒子群算法优化广义回归神经网络的模型参数光滑因子，最后通过实例分析该模型具有良好的预测效果。

深度神经网络模型具有层层堆叠的隐含层结构特征，每层抽取不同的数据特征作为下一层的输入。通过输入输出之间的非线性关系，低级特征可以与高级抽象表示相结合。 目前，LSTM 已成功地解决了许多问题，如负荷预测、股价预测、文本分类等。

1 鲸鱼优化算法

鲸鱼优化算法（Whale Optimization Algorithm，WOA）是近些年提出来的一种新型的群智能算法。原理简单，设置的参数相对较少，拥有很强的全局搜索能力。 鲸鱼优化算法优化特定的问题时，类似鲸鱼捕食的行为。 当猎物出现时，鲸鱼首先会选择潜入到猎物的下方，然后通过旋转的方式向上，对猎物进行攻击时则在其周围形成气泡呈螺旋状。 鲸鱼捕食的过程主要分为3 个过程，分别为环绕猎物、形成螺旋气泡攻击猎物和搜索过程。 对此拟做研究阐释如下。

在捕食的过程中，猎物的位置即为最佳位置，鲸鱼则通过收缩环绕和螺旋来改变自身的位置。 鲸鱼收缩环绕的过程如下：

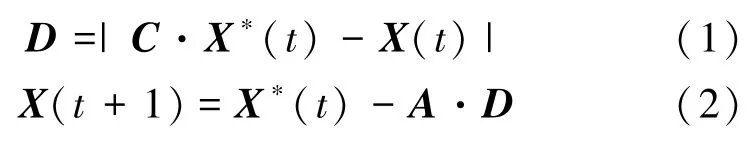
其中，t为当前的迭代次数；X为位置向量；X*为最优位置向量；D为衡量位置的参数；A和C分别表示2 个控制参数向量，通过下式计算可得：

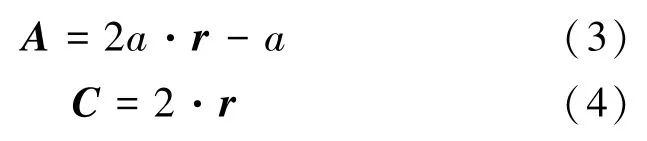
其中，r是0 到1 之间的任意向量，a的值与t和tMaxlter有关，并随着迭代次数的增加而不断减少，这就是收缩环绕行为的体现。 此时涉及的数学公式可写为：

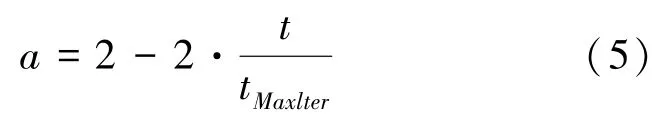
其中，tMaxlter表示最大迭代次数。

鲸鱼通过螺旋方式更新位置的公式如下：

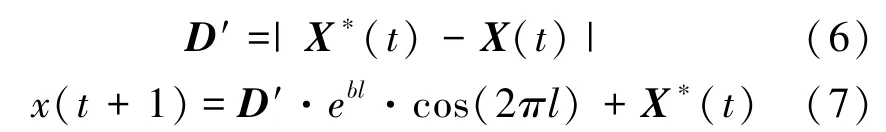
其中，D′表示2 个位置之间的距离；l是任意数，取值在-1 到-2 之间；b为常数，正常情况下取自然数1，具体计算公式为：

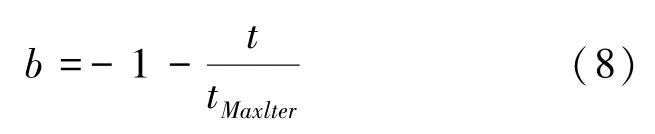
由于鲸鱼在捕食的过程中同时进行收缩环绕和螺旋更新位置，则这两种行为进行的概率皆取1／2，即：

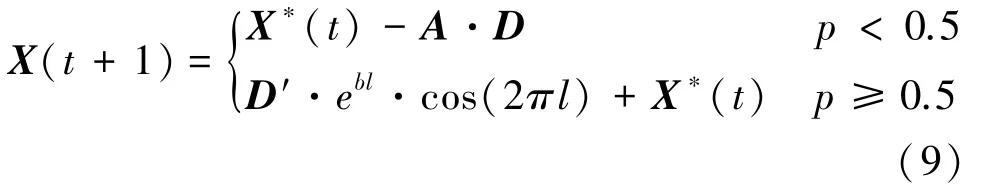
其中，p∈［0，1］。

鲸鱼在捕食的过程中，为到达全局最优位置，会在所处的区域中不断搜索以更新自身的位置，该过程中需用到的数学公式为：

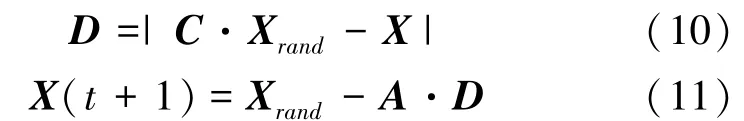
其中，Xrand为位置向量，从当前一代中随机选取。

鲸鱼更新位置的方式是由控制参数向量｜A ｜来决定，当｜A ｜≥1 时，则通过搜索的方式来寻求全局最优解。 当｜A ｜＜1 时，则选择收缩环绕的方式来寻求最优解。 鲸鱼优化算法的流程如图1 所示。

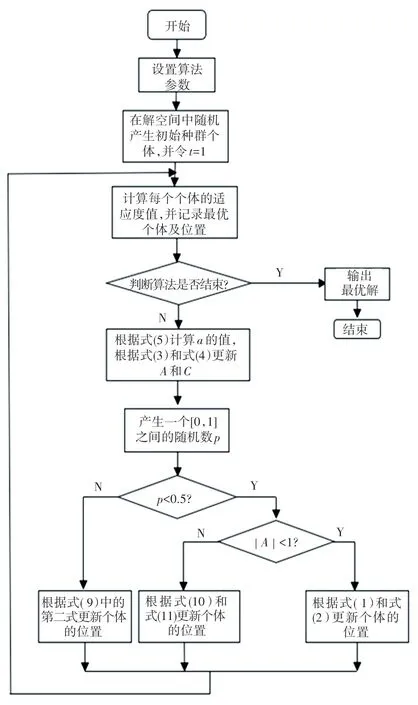
图1 鲸鱼优化算法的流程图Fig.1 Flow chart of the Whale Optimization Algorithm

2 WOA-LSTM 模型

2.1 LSTM 预测模型

LSTM 神经网络首次提出于1997 年，传统的RNN 会出现梯度消失和梯度爆炸等问题，在RNN的基础上改进的LSTM 能够有效地避免这一类问题。 LSTM 的改进之处在于该网络在原先的基础上额外增加了记忆单元，此记忆单元能够记住过往信息并存储。 另外，LSTM 拥有不错的学习能力，能够很好地学习样本的潜在规律，所以能够出色地处理配电网可靠性评估这一类非线性的问题。 LSTM 单元结构如图2 所示。

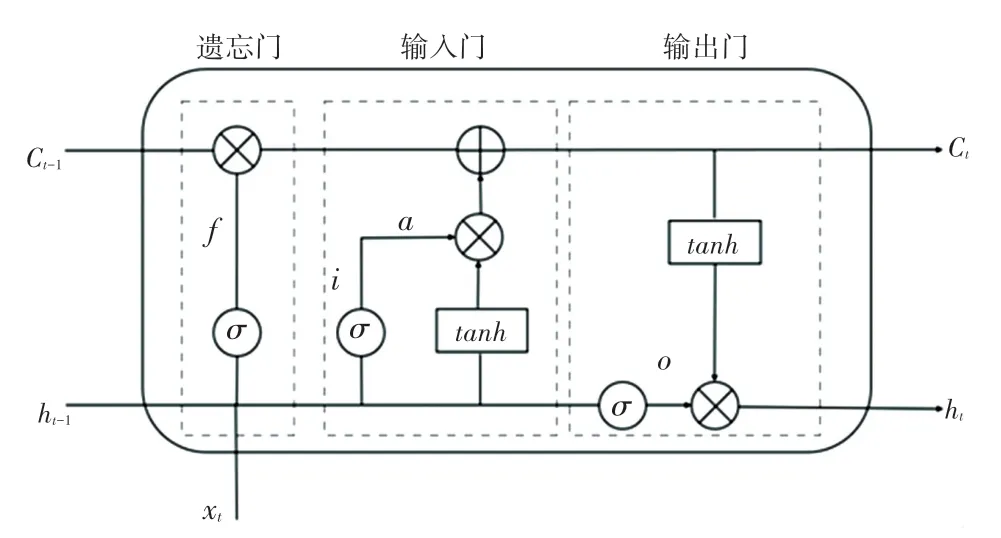
图2 LSTM 的单元结构Fig.2 The unit structure of LSTM

当xt输入时，σ和tanh的作用是决定要更新的数值，同时会生成新的数值。 遗忘门ft会和更新后的数值一起更新单元状态。 输出ht则是由更新后的单元状态Ct经过tanh函数和输出门中ot一起运算后得到的。 遗忘门ft根据上一个时刻的状态Ct-1决定信息的保留还是丢失。 此时，研究中涉及到的数学公式可写为：

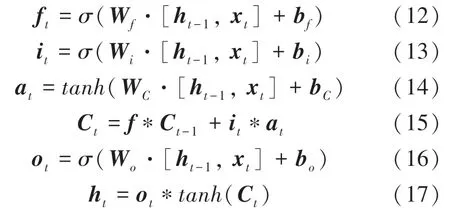
其中，xt为输入向量；ht为输出向量；i表示输入门；o表示输出门；f表示遗忘门；Ct表示当前的时刻状态；Ct-1表示上一时刻的状态；ht-1表示上一时刻的输出；ht表示当前隐藏层单元的输出；σ表示sigmoid激活函数；tanh表示正切函数；W表示权重矩阵；b表示偏差向量。

LSTM 关键参数的选取会影响影响配电网可靠性评估的精度，则需要对模型的参数进行正确选取。鲸鱼优化算法相比其他优化算法具有更加简单的原理，更少的参数，以及更强的全局搜索能力等优点，所以对于处理非线性的问题具有一定的优势，可用于对LSTM 模型参数的选取。

2.2 WOA-LSTM 建模步骤

若采用单一的LSTM 模型进行预测，最后的结果往往不是很好，这是因为LSTM 的迭代次数k，学习率ε和神经元数量L1、L2的取值对模型的精度有很重要的影响，如果这4 个参数选取不合理的话，将会导致建模结果误差大。 因此，利用WOA 较强的寻优能力对LSTM 模型的4 个参数k、ε、L1和L2进行寻优，得到最优参数，以提高建模的精度。 WOALSTM 模型流程图如图3 所示，具体步骤如下：

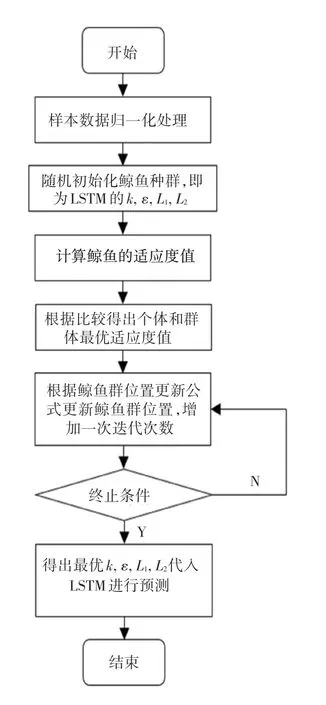
图3 WOA-LSTM 建模流程图Fig.3 WOA-LSTM modeling flowchart

（1）首先对配电网可靠性的数据进行归一化处理。

（2）设定模型的参数，分别为变量数dim、鲸鱼数量SearchAgents_no、变量下限lb和变量上限ub、最大迭代次数tMaxlter。

（3）初始化种群，令n ＝SearchAgents_no，鲸鱼的位置如下式：

计算鲸鱼的第一个随机种群位置X0，迭代次数t取1：

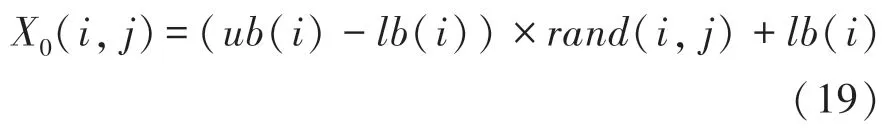
其中，X0（i，j） 为式（18）第i行第j列的值；ub（i） 和lb（i） 为第i个座头鲸的上限和下限；rand（i，j） 为0 到1 之间的随机数。

（4）选取适应度函数：鲸鱼的位置用于表示LSTM 模型的参数L1，L2，ε，k，即X（i，1），X（i，2），X（i，3） 和X（i，4）。 因此将X（i，1），X（i，2），X（i，3），X（i，4）代入LSTM 模型对配电网可靠性进行建模，选择RMSE作为模型的适应度值，RMSE计算公式如下：

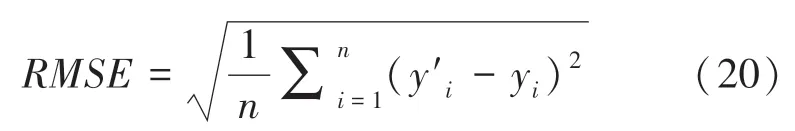
其中，y′i表示预测值，yi表示真实值。

（5）利用WOA 寻优得到最优L1，L2，ε，k。

（6）将寻优得到的k，ε，L1，L2代入LSTM 得到配电网可靠性评估的输出。

3 模型验证

本文将模型的输入分为3 类，即： 配电网网架结构、 配电网元件可靠性参数（线路、变压器、断路器等的故障率及平均故障修复时间）、配电网线路参数（线路长度、线路故障率及线路的类型等）。 模型的输出为以下4 个可靠性指标：系统平均停电频率指标（System average interruption frequency index，SAIFI）、 系统平均停电持续时间指标（System average interruption duration index，SAIDI）、用户平均停电累计时间（Average cumulative outage time，CAIDI）和平均用电可用率指标（Average service availability index，ASAI）作为模型的输出。

将配电网可靠性数据按照比例分为训练样本和测 试 样 本。 设 置 的 参 数 如 下：dim ＝4，SearchAgents_no ＝10，tMaxlter ＝0，lb ＝［10，0.001，1，1］，ub ＝［100，0.01，200，200］。

采用WOA 对LSTM 模型的参数迭代次数、学习率和2 层隐含层神经元个数进行寻优，最终得到较优的LSTM 模型参数，如图4 所示，其中k ＝97，ε ＝0.008 4，L1＝194，L2＝61。

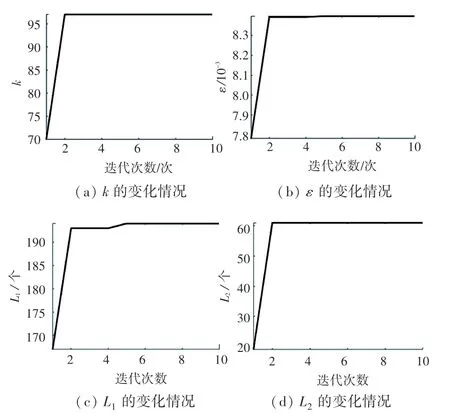
图4 参数k，ε，L1，L2 的变化情况Fig.4 Changes of parameters k， ε， L1， L2

3.1 评价指标和仿真结果

为了更好地描述模型的性能，将均方根误差作为模型的评价指标。 数学公式具体如下：

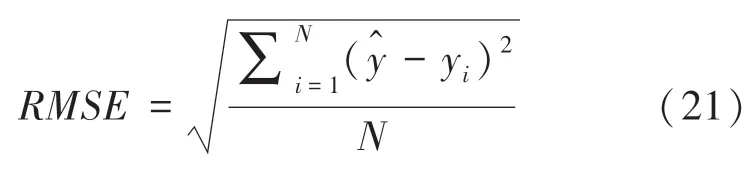
其中，为预测值，yi为真实值。

WOA-LSTM 模型的预测值与真实值的比较曲线如图5 所示。 由图5 可以看出，真实值与预测值十分地接近。 可以说明该模型可以很好地用来做配电网可靠性评估。

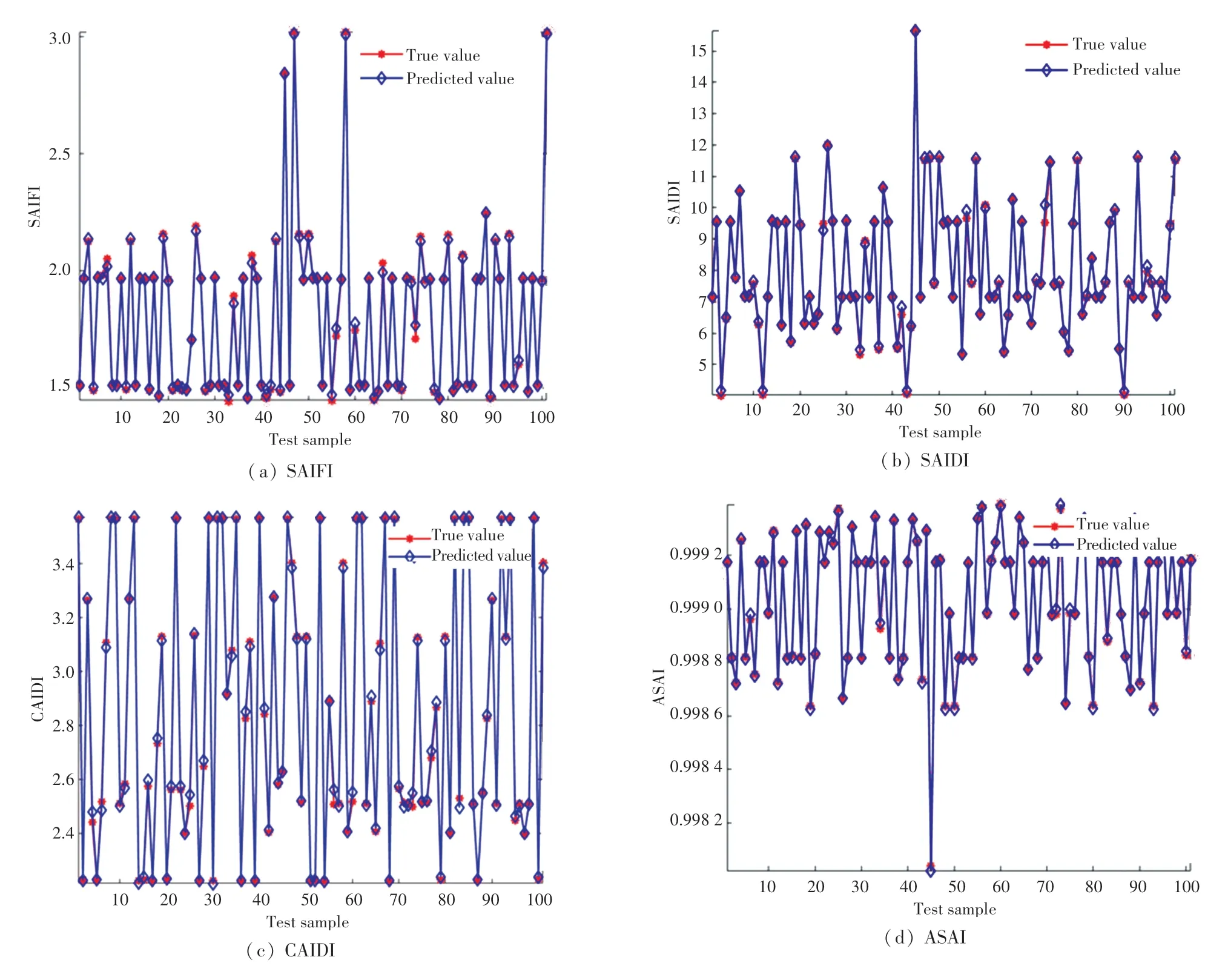
图5 WOA-LSTM 模型真实值与预测值对比Fig.5 Comparison of real and predicted values of WOA-LSTM model

3.2 模型性能对比

为了验证WOA-LSTM 模型的性能，与传统的蒙特卡洛法、深度信念网络模型和LSTM 模型进行对比分析，得到基于Monte Carlo、DBN、LSTM 和WOA-LSTM 的SAIFI、CAIDI、SAIDI 和ASAI 指标的测试集结果如图6 所示。 图6 中，横坐标为101个测试集样本点，纵轴为对应的指标。 从图6 中可以看出，WOA-LSTM 的预测结果与真实值最为接近，效果最好。

表1 给出了Monte Carlo、DBN、LSTM 和WOALSTM 模型的RMSE值。 从图6 和表1 可以看出，相比其他模型，WOA-LSTM 模型的性能最优。 选择其中一个配电网可靠性指标SAIFI 来评价这4 个模型，Monte Carlo 模型的RMSE值为0.472 7，DBN 模型的RMSE值为0.064 3，LSTM 模型的值为0.051 8，而WOA-LSTM 模型的RMSE值为0.013 7，由此则可看出WOA-LSTM 模型的性能更好，精度更高。

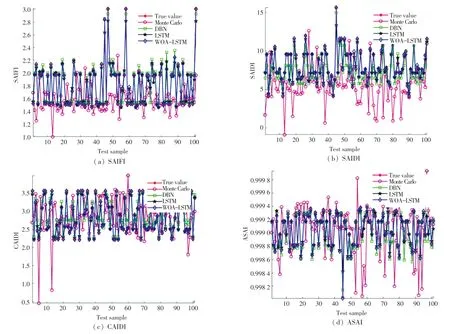
图6 不同模型预测的可靠性指标曲线Fig.6 Reliability index curves predicted by different models

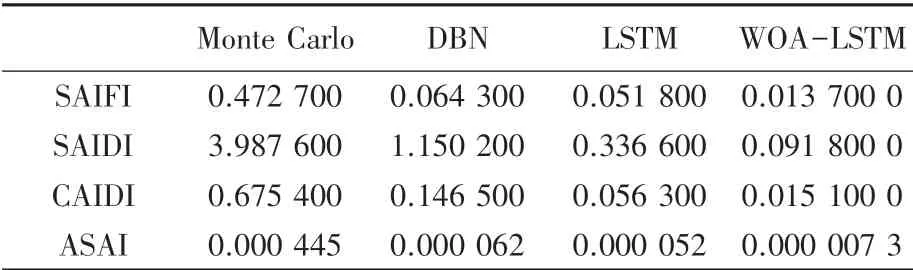
表1 基于Monte Carlo、DBN、LSTM 和WOA-LSTM 的RMSE 值Tab.1 RMSE values based on Monte Carlo， DBN， LSTM and WOA-LSTM

4 结束语

配电网可靠性数据具有十分复杂的特性，每个时间段的可靠性数据都是不一样的，使用LSTM 神经网络进行评估得到了比较理想的效果，但采用没有优化前的LSTM 网络评估效果不是很理想。 本文采用鲸鱼优化算法优化LSTM 网络进行配电网可靠性评估，对LSTM 模型的学习率、隐藏层节点数和迭代次数进行寻优，得到最佳的模型用于配电网可靠性评估。 实验证明，WOA-LSTM 模型的精度相比其他模型效果更好，精度更高，一定程度上说明了深度学习方法在配电网可靠性分析的应用领域具有很大发展潜力。