电动汽车新型无线充电策略的动态建模与效率优化
(国网浙江省电力有限公司金华供电公司,浙江 金华 321000)
0 引言
近年来,国内外学者对磁耦合无线电能传输技术展开了大量的学术研究,并推动了诸多的市场化应用[1-4]。其中,电动汽车是无线充电最重要的应用场景。由于无线充电发射侧与接收侧的非接触性,保证了电源和负载在物理空间上的自由度,从而为电动汽车的动态充电(即边行驶边充电)提供了可能。
目前,DWPT(动态无线充电)依然存在建模方法、供电模式、系统规划及功率智能控制等多方面的难点[5-6]。文献[7]采用状态空间法建立了DWPT 模型,求解了系统电流参数的波形,但计算量大,且无法从全局上分析平均电流的变化规律。文献[8-9]分别研究了DWPT 的补偿网络和耦合结构,得出了DWPT 适宜采用LC-S 补偿和正方形线圈的结论,为系统设计提供了一定的指导。然而,模型仅仅是接收线圈位置不同时的静态状态的融合,并没有考虑汽车速度的影响。韩国KAIST 研发了第一辆DWPT 电动车,发射线圈采用长导轨式充电跑道,这种全局供电的方式会带来不必要的损耗和磁场泄露问题[10-12]。美国北卡罗莱纳州立大学、中国重庆大学等研制了分段导轨式DWPT,并进行了实验[13-16]。汽车行驶时,只有车辆下方的发射线圈才产生激励电流,实现了发射线圈链的局域供电,因而,有效供电区域十分有限,尤其是当接收线圈位于发射线圈边缘部位时,磁场耦合降低,会引起传输效率地急剧下降。
本文提出两发射线圈同时激活的充电策略,保证接收线圈始终处于两发射线圈的合成磁场中。考虑行车速度对感应电动势的影响,建立了含有行车速度的DWPT 电路模型,并分析和优化不同速度、不同电池状态下的DWPT 传输效率。
1 DWPT 系统
1.1 系统组成
两线圈DWPT 的基本结构及其等效电路分别如图1、图2 所示。电动汽车行驶过程中,接收线圈的位置实时地发生变化。为满足动态充电的需求,在路面下方每隔一定的距离设置一组发射线圈,使得汽车在行进过程中始终处于可充电状态,如图1 所示。记相邻两组发射线圈为a 和b,显然a=1,2,…,N-1;b=2,3,…,N。假设接收线圈在y 方向上与发射线圈阵列中心线对齐,电动汽车行进方向为x,高度方向为z。当接收线圈的中心在AB 路径上移动时,相应地,激活发射线圈a 和b,由此,接收线圈置于发射线圈a 和b的合成磁场中,从而感应出电动势,以实现汽车电池的充电。记A,B 两点的间距为l,那么整段道路由N-1 段AB 组成。根据对称性,汽车行驶在每段l 上时无线充电特性是相同的,因而,后续基于AB 路径的研究具有通用性。

图1 DWPT 系统示意

图2 DWPT AB 段的等效电路
当发射线圈a 和b 激活时,可控开关KA和KB闭合,交流电源串联接入2 个线圈中,使发射电流通过图1(b)红色路径形成回路。当汽车进入下一路径BC 时,可控开关KA断开的同时KC闭合,而KB继续保持闭合状态,发射线圈b,c 与交流电源三者串联。通过设置公共母线,每个发射线圈添加一个可控开关,实时检测汽车所处位置、确定可控开关状态,能够实现相邻线圈同时激活的功能。
以AB 路径为例,构造其等效电路,如图2所示。图2 中,高频交流电源us、负载电阻RL分别与发射线圈、接收线圈串联。由于2 个发射线圈的结构完全相同,因此其电气参数也完全相同。R1,R2分别为发射线圈和接收线圈回路的总寄生电阻,由于串联电容的寄生电阻非常小,因此R1,R2可以认为是线圈电感的等效串联电阻。发射线圈与接收线圈间的磁场耦合采用互感来表征。L1,C1分别为发射线圈的自感和谐振电容;而L2,C2则分别为接收线圈的自感和谐振电容。线圈均与各自的谐振电容串联,即系统采用SS型补偿。发射线圈和接收线圈的本征频率分别为谐振时,交流电源频率f,f1和f2均相等。
当电动汽车在动态充电路面上行驶时,系统参数R1,R2,L1,L2,C1,C2是固定值,而互感Ma和Mb是关于接收线圈位置x 的变化量。对于任意的行驶速度v(t),t 时刻汽车所处的位置为x(t)=是时变量。因此,与静态充电中互感M保持不变不同,动态充电过程中,Ma和Mb均会发生实时变化,极大地提高了充电特性分析和控制策略设计的难度。
1.2 感应电动势
根据电磁感应定律,接收线圈上的感应电动势是实现无线充电的关键因素。因此,感应电动势的分析尤为重要。以图3 为例,当线圈1 通过电流i1时,会在自由空间内会产生交流磁场;当交变磁场通过线圈2 界定的闭合曲面时,形成磁通。若已知线圈1 和2 间互感为M12,则线圈2 的磁通为:
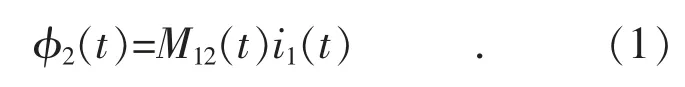
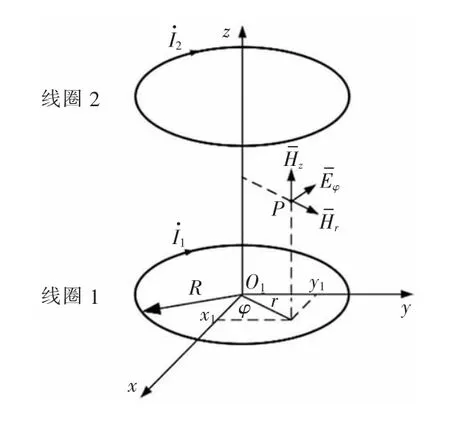
图3 DWPT 线圈间磁场示意
线圈2 两端会产生感应电动势e2,即:
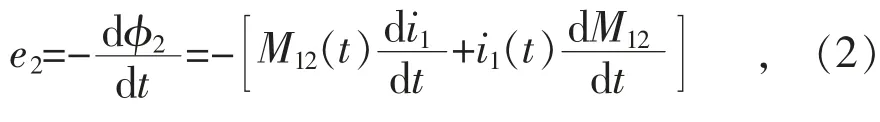
式中:t 时刻的电动势分为两部分,分别为M12(t),前者由电流的变化产生,可以理解为感生电动势;后者的电流不变,但互感发生变化,即线圈移动切割磁感线,可以认为是动生电动势。在静态充电系统中,互感变化率为0,动生电动势也就为0,而在动态充电系统中,显然动生电动势不为0。假设i1(t)=I1sinωt 且定义耦合系数,代入式(2)可得:

式中:G=πk12(t);H=dk12/dt;ω=2πf 是交流电源的角频率,电源频率f通常为几十kHz,如89 kHz。
某典型DWPT 系统l=0.45 m,其耦合系数k12随线圈位置x 的变化曲线见图4。图4 中,曲线1表示仅在发射线圈a 作用下的耦合系数实测值;而曲线2 为发射线圈a 和b 两者的叠加效果。
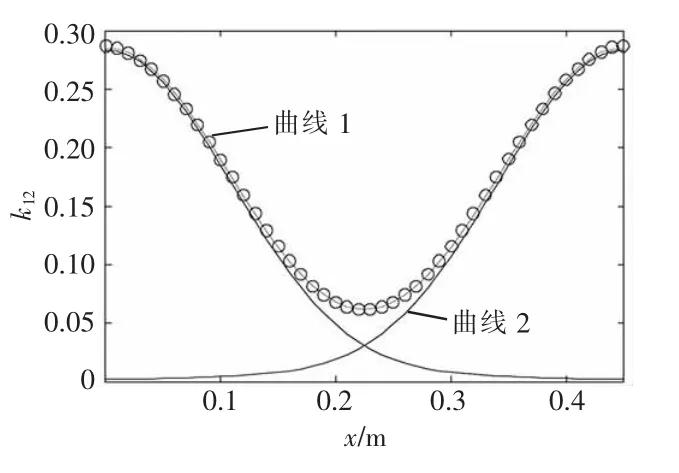
图4 耦合系数随接收线圈位置的变化曲线
k12是位置x 的周期函数,其周期为l。在小段距离l 内,汽车行进速度基本恒定为v,那么k12是频率等于v/l 的周期函数,显然,速度越大,k12的频率越高。当v=33.3 m/s(时速120 km/h)时,k12近似为频率74 Hz 的函数。因此,从时间尺度上看,电流的变化(89 kHz)远快于互感的变化(74 Hz)。记交流电源周期T=1/f,行进周期T1=l/v,那么,行进周期是充电周期的1 000 多倍。由图4的实测数据可得,在一个行进周期内,Gmin=3.41×104,Hmax=51.6,即G≫H,这说明动生电动势远小于感生电动势,在计算过程中可以忽略不计。
1.3 传输效率
根据基尔霍夫电压定律,结合图2 可得,系统电压、电流之间的关系为:

式 中:us(t)=Umsin ωt;M=Ma(t)+Mb(t);L1t=2L1;R1t=2R1;C1t=0.5C1。
在一个交流电源周期即t∈[t0,t0+T]内,时间变化T 小于行进周期T1的千分之一,线圈几乎没有移动,因此,Ma(t)=Ma(t0)和Mb(t)=Mb(t0)成立,即一个交流电源周期内的互感认为是常量。求解式(4)可得各回路电流为:

由Ma(t)=Ma(t0)和Mb(t)=Mb(t0)可知g(t0)=g(t),h(t0)=h(t),不失一般性,式(5)可以改写为:

分析式(6)可知,从小时间尺度(10T)上看,负载电流i2随时间的增大而呈正弦规律变化;从大时间尺度(10T1)上看,随时间的增大,i2在进行正弦变化的同时,其幅度也随之周期性变化。F1(t)和F2(t)决定了i1和i2的幅度,从曲线上看F1(t)和F2(t)分别是i1和i2的包络线。由式(6)可得负载的平均功率和电源的输入功率:

进一步地,可以求得系统的传输效率η=PL/Pin。当发射线圈设计和排布完成后,影响Pin和PL的因素有ω1,ω2和RL。ω1,ω2的调整可以通过改变串联电容C1,C2的容值来实现,而RL是与电池充电状态有关的变化量。当系统运行于传统的谐振状态时,ω=ω1=ω2成立,式(6)可以简化为:

2 DWPT 系统仿真验证
2.1 仿真模型的建立
根据电动汽车和道路的实际物理尺寸,建立DWPT 系统的1/3 缩比模型:发射线圈40×20 cm,接收线圈20×20 cm,传输间距10 cm,2 个发射线圈的中心间距45 cm,如图5 所示。2 个线圈均采用利兹线,绕制成矩形平面的形式,测量该系统的电气参数,结果如表1 和图4 所示。

图5 电动汽车无线充电的1/3 缩比实物

表1 动态WPT 的设计参数
在Simulink 中建立了DWPT 的电路仿真模型,如图6 所示。交流电源的有效值为7.07 V。根据表1 设定系统的固定参数,如各线圈与相应的电容进行串联,从而使其理想的谐振频率达到89 kHz。对于时变互感,Simulink 库里并没有此类元件,那么根据时变电感的端口特性,通过电压控电压源来实现时变互感的模拟,如图6(b)所示。值得注意的是,一次侧电压与二次侧电流的导数成比例关系,这个比例就是时变互感值,它封装在基于图4 实测数据驱动的函数中。电动汽车的使用场景包括高速公路,目前高速公路的平均时速是90 km/h,未来高速公路如杭绍甬高速公路可以达到120 km/h,由于仿真模型尺寸缩小为原物理尺寸的1/3,那么,从电气长度上来看,实际的90 km/h 相当于模型中接收线圈速度v=8.33 m/s,同样地,实际的120 km/h 相当于模型中接收线圈速度v=11.11 m/s。
采用示波器测量交流电源和负载电阻上的电压、电流波形,进而计算得到电源输入功率、负载功率以及传输效率。
当RL和v 取不同值时,仿真得到发射和接收电流波形,同时计算F1(t)和F2(t)的数值,结果分别如图7—图9 所示。由图7—图9 可知,各种情况下F1(t)均是i1(t)的包络线,而F2(t)也与i2(t)的外轮廓基本吻合,这说明了理论分析与仿真结果一致,也验证了式(6)的正确性。为此,可采用式(7)计算和分析负载功率与电源输入功率。与Simulink 建模分析相比,公式法可以在保证精度的同时极大地降低计算量,更适用于系统的优化分析和实时控制。
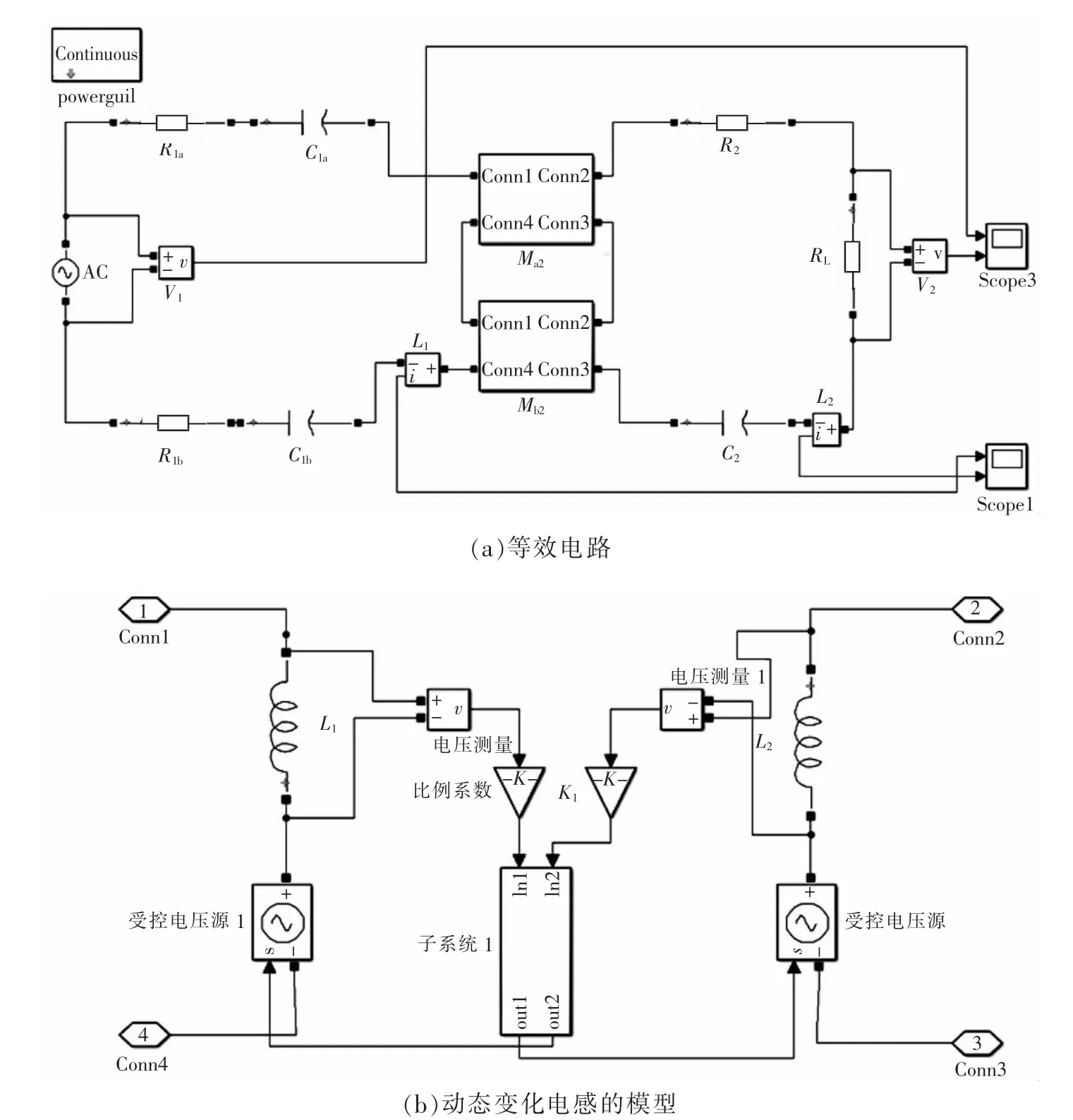
图6 DWPT 的Simulink 仿真模型
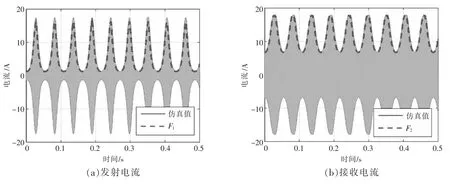
图7 RL=10 Ω 且v=90 km/h 时两侧电流波形

图8 RL=10 Ω 且v=120 km/h 时两侧电流波形
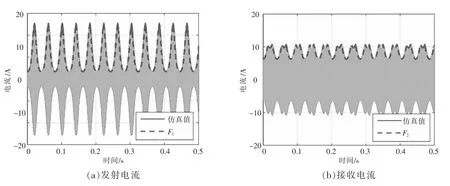
图9 RL=30 Ω 且v=120 km/h 时两侧电流波形
当RL不变而行车速度从90 km/h 增大到120 km/h 时,比较图7 和图8 中的电流波形,无论是i1(t)还是i2(t),其幅值基本相等,而前者的周期数少于后者,因此,行车速度的改变不会影响充电电流的幅值,但会改变充电电流的周期。如果系统后级电路包括整流电路和直流变换电路,那么后级电路的参数设计需要考虑行进速度带来的影响。
当行车速度保持为120 km/h 而RL从10 Ω增大到30 Ω 时,比较图8 和图9 中的电流波形可知,无论是i1(t)还是i2(t),其周期数基本不变,但波形有很大的差异,因此,RL的变化不影响周期,但会影响电流的变化规律。
2.2 传输效率的优化
发射线圈本征频率ω1、接收线圈本征频率ω2与电源角频率ω 均相等,即系统处于谐振状态时,由式(8)可知发射与接收电流、传输效率仅与负载电阻有关,因此,当RL∈[1,50]时,扫描效率值,得到传输效率随RL的变化曲线,如图10所示。图10 中,传输效率随着负载电阻的增大先增大后减小,当RL等于8 Ω 时,传输效率达到最大的75.98%。考虑到汽车动力电池在充电过程中对外表现出来的等效电阻会实时变化,因此,不同负载电阻可以反映电池的不同充电状态。若接收侧无直流变换器,无线充电系统的输出电阻即负载电阻不可控。因此,优化设计的目标是尽可能使传输效率在不同负载电阻下均保持较高值。
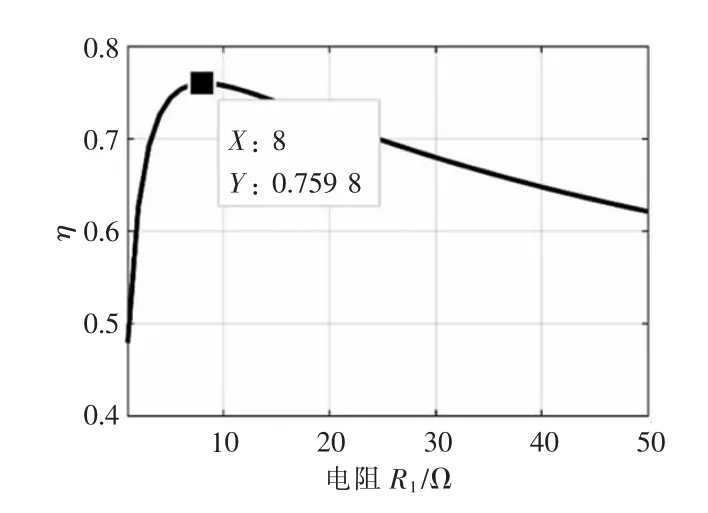
图10 传输效率随负载电阻RL 的变化曲线
由式(6)可知,发射电流和接收电流均是关于发射线圈本征频率ω1、接收线圈本征频率ω2的多元函数。随着负载电阻的变化,ω1=ω2=ω 的传统谐振状态并不一定是最优解,为此,系统设计时可以针对ω1和ω2进行优化分析。
当RL分别取5 Ω,10 Ω,20 Ω 和50 Ω,电源频率保持为f 时,设定f1和f2的范围为[0.85f,1.15f],计算得到不同本征频率的组合下,传输效率的曲面图,如图11 所示。
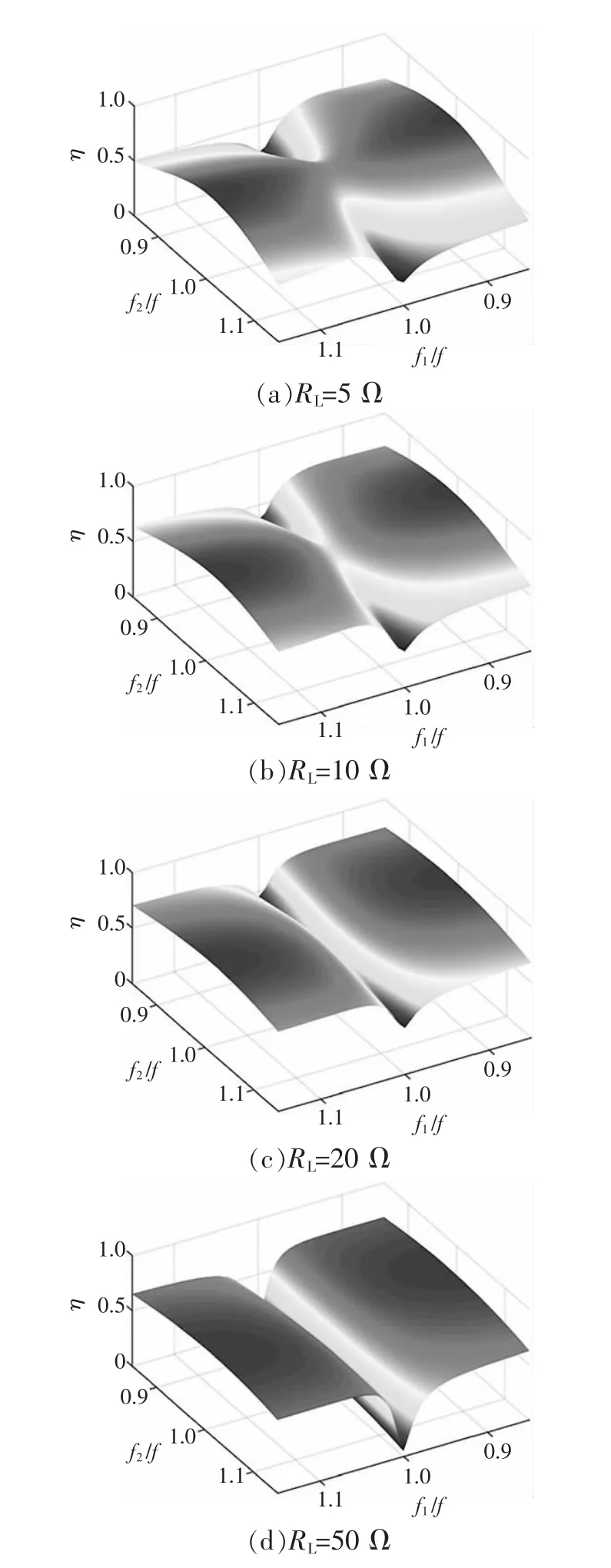
图11 当负载电阻不同时传输效率随发射线圈和接收线圈本征频率的变化曲面
图11(a)在f1=f 的附近,曲面出现了2 个对称的坑道,伴随着RL的增大,坑道逐渐合并形成效率下降的沟道,而且效率下降幅度也逐渐增大。当RL等于5 Ω 或10 Ω 时,谐振点基本在最大值附近;而RL增大到20 Ω 或50 Ω 时,谐振点均在极小值点。因此,从RL的全范围来看,谐振状态并不是最优状态。观察图11 进一步可得,当f1固定时,传输效率是f2的单峰函数,最大值基本出现在f2=f 处。当f2=f 且f1适当地偏移(增大或减小)电源频率f 后,传输效率能达到最大值。f1的适度调整通过改变串联电容来实现,由于串联电容大约12 nF,容值较小,考虑到耐高频耐高压高精度的电容器容值越低,制造难度越高,因此,适宜采用低频段的区域,即将串联电容C1值适当调大,以实现效率的提升。
综上所述,本征频率确定为f1=0.85f 和f2=f,计算本征频率优化前后的传输效率,结果如图12所示。显然,优化后传输效率在整个负载电阻的范围内均得到了有效地提升,且在高阻值区域愈加明显。由于实际系统设计会对传输效率提出要求,如不低于85%,此时需要将负载电阻限定为8 Ω 图12 本征频率优化前后传输效率的对比 针对高速行驶的电动汽车,本文提出了基于接收线圈位置所在区域的相邻两发射线圈同时激活的充电策略,并由此建立其DWPT 系统的模型。与静态充电系统相比,动态模型中增加了速度因素,并推导了发射电流和接收电流的控制方程。将两侧电流的理论变化与仿真结果进行了对比,验证了控制方程的准确性,从而为控制方程用于优化设计提供了理论依据。针对电池不同充电状态下均需要较高传输效率的需求,优化发现适当降低发射线圈的本征频率可以有效提高各工况下的传输效率。下一步工作是制作DWPT 的样机并进行实验验证,同时需要进一步探讨动态切换时产生的噪声及效率的损失问题。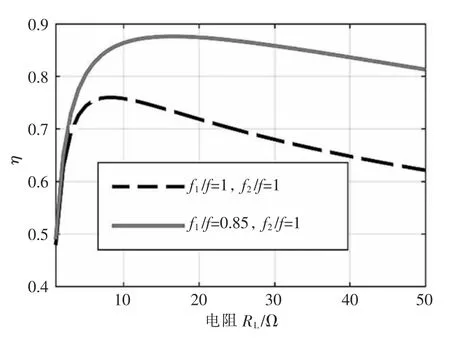
3 结论

