基于有效稠密序列提取的用户评分数据增强及二值评分转换策略

崔北亮，周小康，李树青

1.南京工业大学图书馆，江苏 南京 210009

2.南京财经大学信息工程学院，江苏 南京 210023

推荐系统在日常生活中的应用变得非常普遍，有学者据此断言“我们正在离开信息时代，进入推荐时代”［1］。目前，推荐系统已被广泛应用于人工智能［2］、电子商务［3］、数字图书馆［4］等应用系统中，越来越多的网站和社交媒体的竞争开始逐渐转变为个性化推荐服务的竞争。推荐系统的目的正在于基于已有的用户兴趣历史记录来判断用户未来的可能兴趣点，以便推荐给用户尚未关注到的潜在感兴趣内容。因此，如何根据用户的浏览信息或者购买情况推荐更符合用户兴趣的项目是推荐系统面临的一个重大挑战。

改进推荐系统的算法不能完全建立在算法自身的完善上，而作为目前所有推荐系统算法的关键内容——数据本身，却并没有受到人们过多的重视。这给现有推荐系统算法改进提供了一个有益的研究思路，即如何有效选择数据，通过数据增强等方式来获得更为准确的用户兴趣模式的表达能力［5］。

协同过滤是一种非常有效而且应用广泛的个性化推荐技术［6］，它基于一个简单的假设，那就是用户过去的兴趣代表着未来的兴趣。因此，通过分析已有的用户兴趣信息（这主要由用户对项目的评分来体现），就可以对未来未知项目的评分做出预测。这个假设在一定程度上具有合理性，如有学者利用招聘信息网站上的用户数据分析发现，对于每个用户，在过去14周内平均有2/7的项目会被用户在第15周再次点击［7］。具体而言，协同过滤推荐方法是通过获取和当前用户相似的其他用户，来给当前的用户提供合适的意见或者项目。其优点在于不需要了解项目的具体内容信息，也可以为用户推荐新的可能感兴趣内容。然而传统的协同过滤算法也存在着很多的不足，比如传统协同过滤算法中使用的评分是否可以有效表达用户真实兴趣并没有得到准确的验证，再如传统协同过滤算法无法处理过于稀疏的数据，此时易于产生相似度计算不准确的问题。

因此，这些构成了本文研究的两个主要关注点：

（1）本文探究和验证了如何在数据层面上获取更为准确表达用户真实兴趣的新方式。当前大部分学者都认为评分行为是一种非常有效的判断用户兴趣的方式，现有的研究方法也大都基于这个假设。但是，用户评价与否是否可以表征用户的兴趣，或者说相对于评分的具体数值，评分与否这种二值性（Binary）是否更有价值，这种问题也被称为“二值视图（Binary view）”［8］。 从用户的动机角度来思考，用户之所以在推荐的项目中有选择地选择部分项目而忽略其他项目，这本身就体现了一种用户兴趣的差异性。因此，用户不去对项目进行评价的过程本非随机现象［9］。现有的评分因为都是用户对自己想关注的项目进行评价，通常评分更易于取得较高的数值，而且还会对很多基于评分的推荐算法本身产生不利的影响。有效地利用这些遗漏项目和进一步理解现有打分数据，对于改善基于评分的各种推荐方法十分必要［10］。

（2）本文探究了如何解决数据稀疏给协同过滤方法带来的计算有效性问题。本文重点研究了基于有效稠密子序列的协同过滤推荐算法有效性的计算问题，即通过在已有的用户评分记录中合理选择有效稠密子序列，增加有效数据的稠密度，减少了噪声数据的不利干扰。考虑到这种改进会带来数据稀疏度问题，本文通过分析项目的属性特征并结合用户的有效时间区间识别用户的高概率参与项目，对数据进行填充。同时，本文还使用用户兴趣变化一致性来深入研究分析用户评分信息与用户是否评价来验证用户需求方面的效果，据此结合第一种方法的思路，提出了一种根据用户是否评价的二值数据来替换传统具体评分数值的数据表达方法，实验证明采用用户是否评价的二值数据会取得更为优异的实验结果。

1 相关工作

传统的协同过滤算法主要包括3个重要步骤，分别为获取数据、寻找最近邻元素、预测推荐。在整个算法过程中，对结果准确率影响最大的就是数据稀疏问题。丁少衡等［11］为解决协同过滤推荐系统数据稀疏带来的问题，使用Sigmoid函数来实现数据稀疏状态下用户相似度计算中的用户属性和用户评分信息平滑过渡，毛宜钰等［12］也提出使用Sigmoid函数来处理用户评分存在的数据稀疏性问题。钱刃等［13］提出用融合稀疏度进行加权的协同过滤算法来解决稀疏性问题，该算法中重新定义了矩阵稀疏度计算方法，然后融合矩阵稀疏度对用户相似度进行加权，并以此来改进协同过滤算法。为了有效挖掘用户兴趣的变化趋势，很多学者提出基于用户兴趣变化的协同过滤推荐算法，如于洪等［14］通过遗忘曲线来观察用户兴趣以达到适应用户兴趣变化的目的，贾伟洋等［15］利用用户兴趣贴近度对相似度结果进行进一步加权处理，得到的相似度结果中融合了用户的兴趣偏好信息。

关于二值视图问题，可以将用户是否评价作为最为简单的一种隐式信息，把用户是否对项目产生过评分设定为一个二进制值，据此来表示伪隐式评分（Pseudo⁃implicit rating）。由于用户对于项目评价并非是一种随机行为，评价行为本身就反映了一种用户对项目的偏好信息［16］。即使这种信息并非很充分，但是和单纯使用显式用户信息的方法相比，集成该隐式信息到现有显式信息中可以增加推荐系统的预测准确度［17］。

对于不评价的项目既有可能是用户不喜欢，更有可能是用户根本没看到，可以称之为用户曝光（User exposure）问题［9］。 比如不评分不能完全看成是项目的问题，也有可能来自于用户的意愿，比如用户只对特别喜欢和特别不喜欢的项目才去评价。在一定程度上，可以把这种用户是否评价看成是一种隐式信息，它和评分信息具有一定的关联性，加以有效利用可以提高传统基于评分方法的推荐系统效果［18］。 此时，评分矩阵（Ratings matrix）简化为二值矩阵（Binary matrix）。

对于评分矩阵中缺失项目的理解和考虑已经成为一种非常有效的方法［19］，比如作为隐式的负反馈来训练推荐系统［20］。还有文献对遗漏数据模型的低阶特征（Low rank nature）进行研究，并推导出系统性能的底线［21］。在无法从评分直接判断用户的喜好时，这些被经常显示的项目也被其他学者认为应该排在推荐列表的后面［22］。

和这些已有的方法不同，本文所提出的方法主要在不改变现有原始数据的基础上，通过有效的数据选择，提取有效稠密数据子集，这也给现有推荐系统中数据稀疏问题解决提供了一种新的思路和可行性。本文从实验验证的角度，探索结合二值视图数据在表达用户真实兴趣中的价值，并据此完成了现有推荐算法的改进。同时，对于推荐系统应用中的相似度问题，已有学者通过利用人口统计学信息实现用户相似度的测度［23］，还有学者利用模糊聚类方法实现项目聚类，得到潜在相似关系集合并分区，最终以分区为单元实现相似度的并行计算［24］。本文根据二值评分数据的特点，探索基于二值评分数据的相似度计算及项目评分预测方法。

2 二值评分转换策略设计及应用

2.1 用户评分数据的有效稠密序列

通过观察传统的协同过滤算法，可以发现在用户评分矩阵中，每个用户都存在大部分未参与项目，这会导致数据变得异常稀疏，为了缓解这些难以避免的问题，本文提出利用有效稠密序列的方法进行改进。

步骤分为两步：第一步是对用户的评分序列进行筛选，过滤序列中用户参与的不感兴趣项，并以用户存在潜在兴趣且未参与的项目对数据序列进行填充，形成新的用户评分子序列，据此缓解数据稀疏问题；第二步是根据评分发生的有效时间区间，再次对用户评分序列进行子序列提取，用二值数据进行转换表示，并提出改进后的用户相似度方法。

具体说明如下：

（1）用户评分子序列的提取和填充

根据每个用户评分项目获取相关的项目属性特征，并统计这些特征的分布情况，可以定义出现次数最少的特征为低兴趣类，出现次数最多的则为高兴趣类。本文认为拥有低兴趣类特征且没有高兴趣类特征的项目为不感兴趣项，例如某用户对观看的大量动作类电影和少量恐怖类电影都给出了低评分，虽然评分低，但是观看数量则可以说明该用户对动作类电影更感兴趣，评分过低的原因有可能是影片自身质量问题，而对于恐怖电影则是不感兴趣。因此可以将这些不感兴趣项目进行过滤删除，形成了新的用户评分子序列。

为了解决过滤删除引起的数据稀疏问题，本文进一步将用户未参与且拥有高兴趣类特征的项目数据作为用户高概率感兴趣的内容进行数据填充。在实际计算中，又可能因为用户行为不活跃，参与的项目相对较少，导致项目的特征属性类型统计也会很少，因此需要定义一个约束阈值，当累计出现最高的项目属性特征数量超过用户所参与的项目数量的一半时，则可以看成是用户高概率参与的项目。

筛选出用户参与评价的起止时间内所有符合这些属性特征的项目，使用该用户的平均评分为这类项目生成评分数据。在数据生成中遇到生成的数据与源数据中的数据重合时，保留源数据中的真实数据。

算法伪代码为

（2）用户评分子序列的二值评分转换

在第一步得出的每个用户新评分序列基础上，根据用户参与每个项目的评价时间，可以得到其参与评价的总起止时间区间。将需要比较计算的两名用户的时间区间进行综合，可以得出一个新的时间区间。进一步，可以筛选出总数据集中处于此时间范围的所有项目，假设用户u评价过的最早与最晚的项目分别在2012年和2019年，用户v评价过的最早与最晚的项目时间为2010年和2015年，选取用户u和用户v整体的最早评价时间与最晚评价时间，分别为 2010年和 2019年，那么选取时间在［2010，2019］之间的所有评分项目构成新的评分子序列，需要提及一点，不同的两个用户所得到的时间区间可能会不同。

两个用户形成的大时间区间，包括了所有参与和未参与的项目内容。已有的新用户评分子序列，可以进行评分数据的二值转换，即根据用户是否参与评分作为标准，可以认为此时的用户参与评分代表其对该项目存在潜在兴趣，将二值评分设置为“1”，未参与评价项目设置为“0”，从而得到两名用户各自的二值评分序列。

算法伪代码为

2.2 二值评分数据的有效性验证方法设计

前文已经说明，用户是否已经评价的二值评分数据可以被理解为一种潜在用户兴趣，即用户在没有给项目评分之前，完全凭借自己的兴趣爱好选择的项目就能代表用户的潜在兴趣。比如在现实生活中，人们看一部电影，往往不是因为听别人说这部电影非常好看才去看，也不会因为这部电影的评分很高就去看，更多情况下是这部电影是自己喜欢的类型才会有选择性地去看。正因如此，当两个人都是因为各自的潜在兴趣去选择同一部电影时，通过相互之间的分析，可以更准确预测其他事物的结果。

拿电影数据集来举例，传统协同过滤算法评分矩阵中的数据是用户对电影的评分值，那么这个评分值是在用户看完这部电影之后，给出的对这部电影的评价，如果评分为4分或者5分，可以认为用户喜欢这部电影，也可以认为用户是出于对这类电影的喜爱，又或者是用户只是喜欢这部电影的主演而已，原因因人而异，想把众多原因整合到一起，工作量非常巨大并且难以实现。因此，基于用户是否评价的二值数据表达，可以提供一种只研究用户兴趣的简单方法，不需要关注用户给一部电影打了多少分，也不需要关注用户到底是基于什么原因给电影打分，只需要关注用户有没有看过这部电影，如果看过，则标记用户与电影之间的关系为“1”，否则为“0”。

这种新型数据表达的思路需要实验的验证，为此设计如下验证实验。

实验方法：通过用户过去与未来的评分项目类型相似度来比较二值数据与评分数据对用户兴趣的表达有效性。

实验步骤：

（1）每个用户按评分时间先后顺序将其评价项目分成训练集和测试集，其中训练集中的数据为用户过去评价的项目，测试集中的数据为用户将来评价的项目；

（2）训练集中每一个用户的评价项目类型数目形成向量，同样方式找到测试集中的序列形成向量，形成待比较的两个向量；

（3）将每个用户得到的二值评分向量进行相似度计算，相似度计算方法采用的是2.3节中的式（1），最终将所有用户的相似度取平均值。

2.3 基于二值评分数据的相似度计算及评分预测

传统协同过滤中常见的相似度计算方法无法进行二值评分数据向量的相似度比较，如使用余弦相似度去计算，就会造成分母为0的无意义情况，而使用调整余弦相似度和皮尔逊［25］相似度计算则不可避免地需要计算评分的平均值，对于二值数据而言，平均值没有任何意义。因此借鉴文献［26］使用式（1）计算谷本系数相似度。

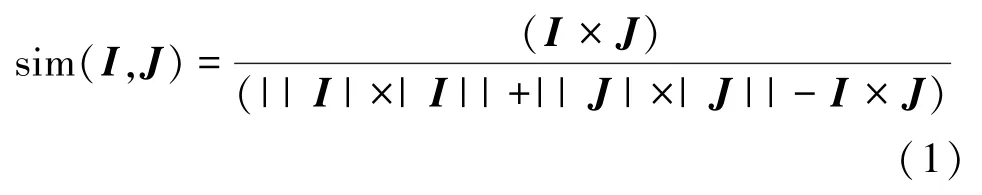
而余弦相似度的向量表示形式为

式（1）和式（2）中，I，J分别为两个不同用户的评分向量，式（1）计算结果约束在区间［0，1］之间，较皮尔逊相关相似度［－1，1］的结果区间更方便算法后期的计算。

经过相似度计算之后，可以取相似度最高的若干结果作为最近邻居集合，再次利用原始评分数据来进行评分预测，预测值计算方法为

式中，L表示源数据经过2.1节之后最终得到的数据集合，表示用户a对所有项目评分的平均值，表示用户b对所有项目评分的平均值，rb，i表示用户b对项目i的评分，sim（a，b）为用户a与用户b的相似度，N为最近邻居集合。

具体算法的步骤过程说明如下。

输入：数据集中划分好训练集与测试集，最近邻居个数num。

输出：用户a对测试集中项目i评分的预测值。

算法步骤：

步骤1使用2.1节的方法对训练集中的每个用户进行有效评分稠密序列的提取和填充，然后进行用户评分序列的二值数据转换；

步骤2利用式（1）计算任意比较用户之间的用户相似度，利用式（2）计算用户a与用户b之间的用户相似度；

步骤3根据计算的用户相似度来寻找最近邻居，并使用式（3）计算用户a对测试集中项目评分的预测值。

算法伪代码为

3 实验与结果分析

3.1 数据集和评价方法

本文选用的是 ml⁃latest⁃small数据集，数据结构如表1所示。

表1 数据集结构表

评分预测效果的评价标准选择了RMSE（均方根误差）和F值（正确率和召回率的调和平均值）两种指标。两个指标的计算公式分别为

式中，X可以理解为用户的集合，函数h（x）为评分预测模型预测的评分，yi为每个用户对项目的真实评分。其中正确率和召回率的计算方法如下：

正确率＝提取出的正确信息条数/提取出的信息条数；

召回率＝提取出的正确信息条数/样本中的信息条数。针对不同数据集正确率和召回率的计算公式也随着数据集结构的不同而重新定义，本文根据实验数据的特点，规则定义如下：

正确信息条数。预测数据满足与真实数据差值绝对值低于0.5的总数据个数；

提取出的信息条数。预测数据值高于3的总数据个数；

样本中的信息条数。真实数据值高于3的总数据个数。

3.2 数据集划分的有效性

在进行实验之前，验证数据集划分的有效性尤为重要，本文划分数据集的方式是按照用户参与项目的时间先后顺序来进行。表2～4给出按照不同比例划分 ml⁃latest⁃small的情况（其中相似度指标使用式（2））。

表2 60%训练，40%测试评分分布情况（整体分布的相似度为0.998 40）

表3 50%训练，50%测试评分分布情况（整体分布的相似度为0.998 56）

表4 40%训练，60%测试评分分布情况（整体分布的相似度为0.998 61）

通过表2～4对数据集划分后的评分数据分析，不同比例划分数据集之后，每组训练集和测试集的评分区间数量构成的向量相似度高达99%，更符合用户的兴趣情况，因此本文以用户参与项目的时间来划分数据集合理有效。

3.3 结果分析

3.3.1 二值评分数据的有效性验证实验

按照不同的比例划分训练集和测试集，可以得到二值评分数据的有效性验证实验结果，如表5所示。

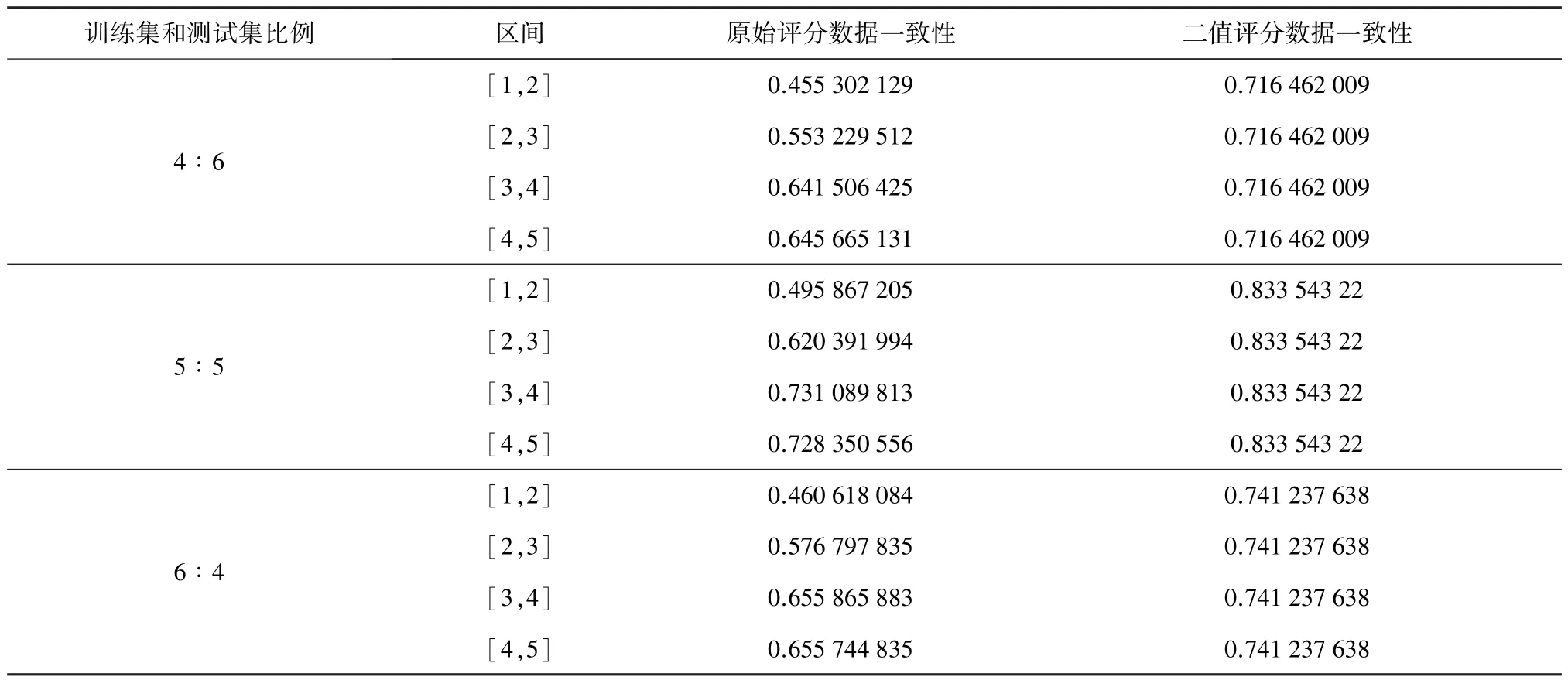
表5 不同训练集和测试集比例下评分数据和二值数据的一致性比较

由表5发现使用二值方法计算出来的过去和未来电影类型的相似度明显比不同区间评分值计算出来的高很多，其中5∶5的比例划分训练集和测试集的一致性最高。同时，对于原始评分而言，在不同分值区间的一致性差异比较大，总体来看，高分一致性要优于低分一致性。

通过上述比较，二值评分方法的一致性不论是效果还是稳定性都优于原始评分方法。因此，使用二值数据的评分表达方法要比使用原始评分的方法更能体现用户兴趣的一致性。

3.3.2 二值评分数据和原始评分数据的评分预测效果比较

实验结果通过RMSE和F值进行比较，具体如图1和表6所示。

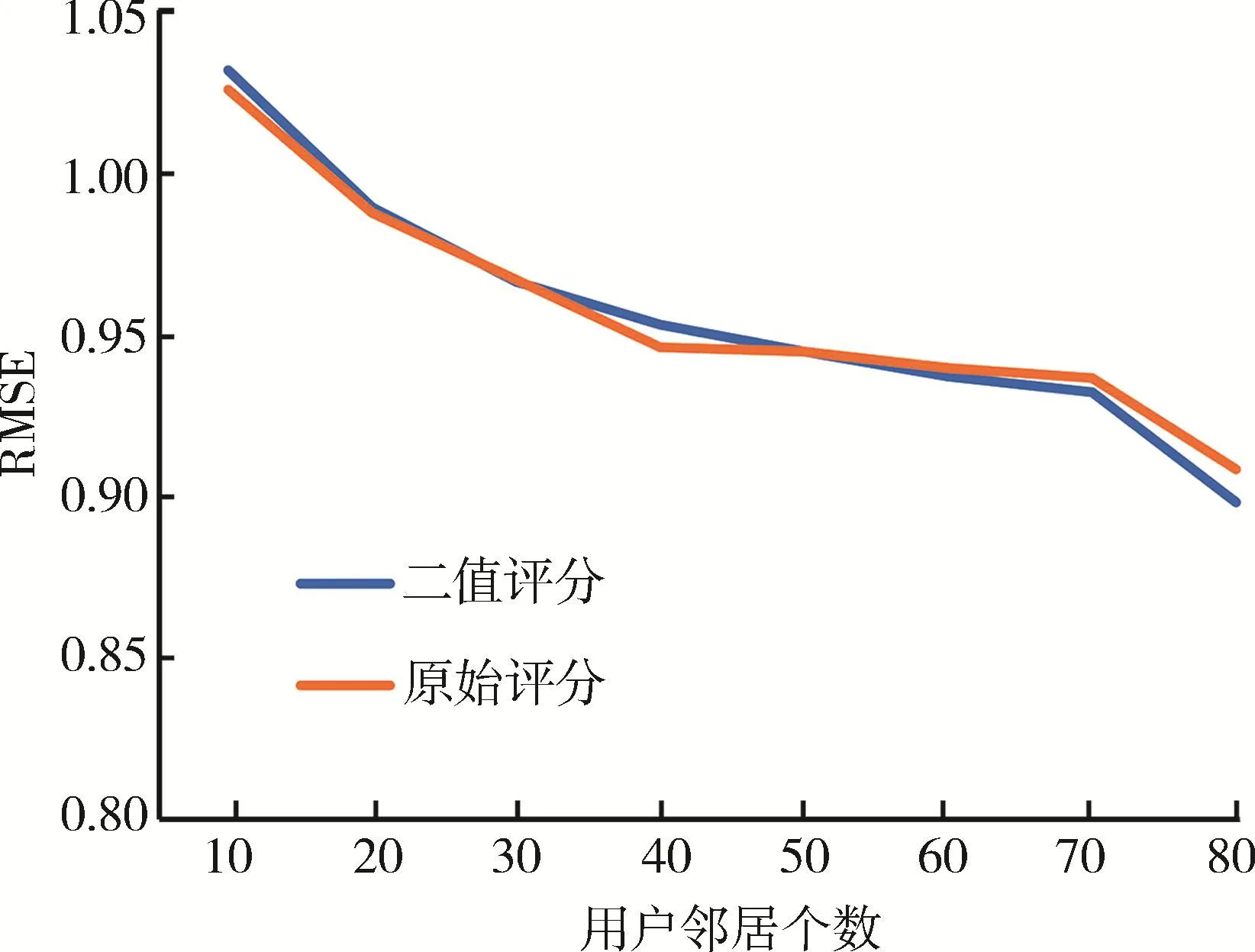
图1 二值数据和原始评分数据评分预测效果的RMSE值比较

表6 二值评分数据和原始评分数据评分预测效果的准确率、召回率、F值比较

由图1可以看出，随着最近邻居的增多，在算法中使用二值评分数据的RMSE值越来越小，最终低于算法中使用评分数据得到的结果。表6数据中展示了评分预测算法比较重要的几个指标数据，从中可以看出，算法中使用二值评分数据在准确率、召回率以及准确率和召回率的调和平均值（F）都要比使用评分值数据高，结合3.3.1节的实验结果，可以认为使用二值评分数据不仅能更准确地定位用户的兴趣，还可以为评分预测算法的效果带来一定的优化。

3.3.3 与经典评分预测算法的效果比较

该实验主要验证结合本文所提出的用户评分数据的有效稠密序列提取和填充方法的有效性，同时，在以下对比实验中，改进算法将直接使用二值数据代替评分数据。

RMSE指标的比较结果如图2所示。

图2 不同评分预测方法的RMSE值比较

图2 中，NMF（Non⁃negative matrix factorization）为非负矩阵分解方法。可以看出，本文提出的改进算法相比其他经典算法，在不同最近邻居数量的情况下，评分预测效果的准确率都比较高，尤其和除标准协同过滤方法外的其他方法相比，准确度的稳定性较强。而且，随着最近邻居数量的不断增加，效果不断提高，最优值达到0.898 8。

准确率、召回率、F值指标的比较结果如表7和表8所示。

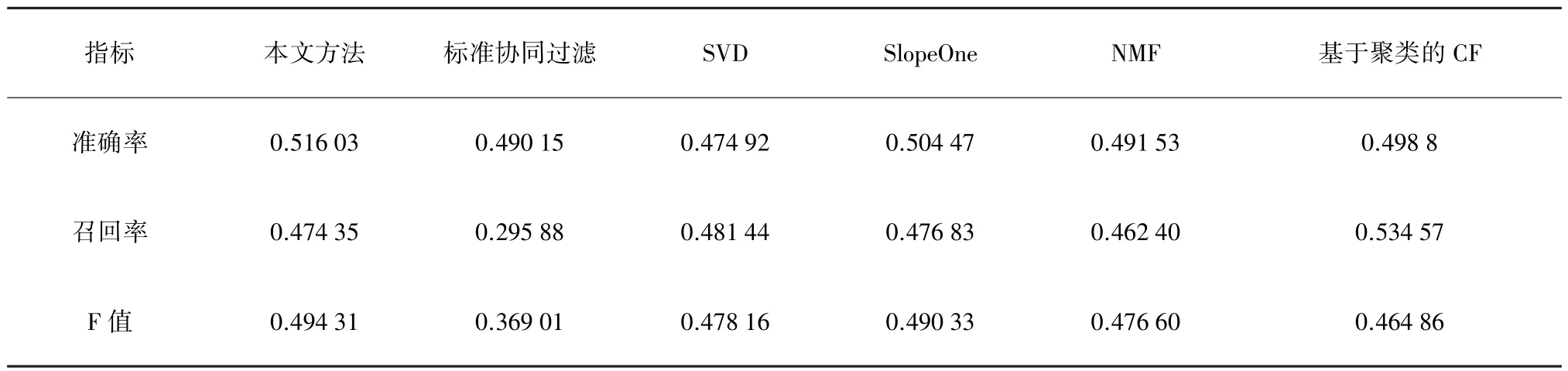
表7 不同评分预测方法的准确率、召回率、F值比较

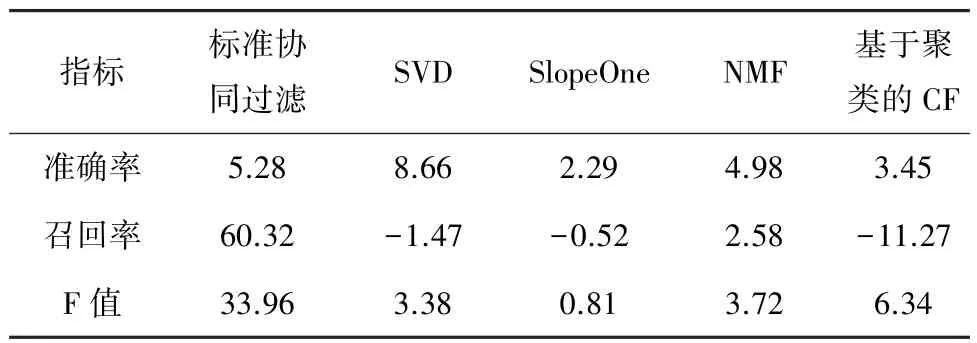
表8 本文方法比其他评分预测方法的准确率、召回率、F值的提高率 %

由表7、8可以看出，本文提出的改进算法相比其他经典算法，3个指标普遍提高，其中准确率和F值提高最为明显，和其他方法相比，都取得更好的指标值，其中准确度最高提高8.66%，F值最高提高33.96%。召回率和部分方法相比有所下降。可见，本文所提方法更适合侧重于准确率指标的海量数据推荐场景下推荐系统的服务应用。

4 结束语

本文通过提取用户评分信息中的有效稠密序列和生成有效数据的方法来改进传统协同过滤算法，在此基础上对比研究了用户原始评分值和是否评分的二值评分数据对用户兴趣表达的有效性。该方法综合利用了用户评分数据的有效稠密序列提取方法和二值评分转换方法，在此基础上实现了相似度计算方法的改进，实验证明方法有效。

本文所提出的改进协同过滤算法不仅利用稠密序列和数值填充等数据增强方式克服了数据稀疏性问题带来的不利影响，同时还可以更准确地识别用户兴趣特征。但是在本文改进的算法中，使用用户是否评分的二值数据相较于原始评分值的优化改进仍然还有很大的空间，同时在提高召回率方面也需要进一步优化，这些都构成了本文后续研究的主要侧重点。