基于数字图像技术的静压桩周土体位移规律分析

姜 赟 , 陆 烨, 王校勇

(1.上海大学土木工程系, 上海 200444;2.上海勘察设计研究院(集团)有限公司, 上海 200093)

静压桩具有施工速度快、无污染、完成性高等优势[1], 在工程建设中被大规模推广.尤其在软土地区以及不允许有强烈振动的地方, 静压桩是一种有效施工方法.但随着桩体的压入,桩周土体的侧向挤压、浅部地表的隆起、桩端部侧向下的压缩剪切等强扰动大变形行为会不可避免地对相邻的既有建筑物及环境产生影响[2].

围绕静压桩沉桩挤土效应, 越来越多的学者开展了大量研究, 其中包括用有限元模拟的结果与现场实际测得的不同深度的土体位移进行对比[3].然而, 由于现场试验成本过高, 使得部分研究大多集中在室内通过模型试验来完成[4-5].为了直接测得桩周土体位移场的情况, 很多学者采用数字图像相关(digital image correlation, DIC)技术来完成.DIC 技术是变形场非界面量测的一种简便、经济且实用的途径, 例如, 在固体和流体力学领域中应用较多的粒子图像测速技术(particle image velocimetry, PIV)[6-7].在采用DIC 技术研究压桩的试验[8-11]中, 有的学者采用透明土和自行设计的静压桩模型试验系统, 但是由于透明土土样性质和透明度制备的特殊性, 模型箱与桩体尺寸都受到限制;有的采用半模桩并观测土体中标志点移动情况来得到得到土体的位移场, 但需要人为设置固定的标记点, 且研究大多集中在压桩结束时的最终位移.另外, 压入过程中桩周土体位移变化规律及其与土压力的关系方面的研究也较少.

当桩被压入砂土中时, 桩体表面与土体相互作用, 形成具有大量颗粒旋转和平移特征的剪切带扰动区.在压桩过程中, 扰动薄层很难被捕捉观察, 因此对压桩模型试验观察扰动层[12]的研究有限.有的研究人员使用界面剪切试验研究该区域中的颗粒位移[13-14], 但这与真实的剪切扰动区规律有所区别.

本工作采用DIC 图像技术研究沉桩压入过程中土体位移变化情况, 同时对剪切扰动区域的颗粒位移进行跟踪, 监测压桩过程中土体中产生的应力, 分析并得了到土体应力及相应位移的规律.

1 试 验

1.1 模型装置

图1 为试验采用的模型装置, 包括模型箱、加载系统、数码相机、模型桩、摄影灯等.模型箱尺寸为1 m×1 m×1 m, 上部配备电控液压千斤顶, 装载能力为10 t, 模型桩采用半圆铝合金桩, 半径R为25 mm, 长Lo为550 mm, 无桩尖(180◦).与文献[8-9]中的试验装置(桩径5.7∼10 mm)相比, 本工作扩大了模型箱和桩的尺寸.试验过程中, 桩体最终贯入深度为450 mm, 贯入速度为2.5 mm/s.为了监测压桩引起的侧向土应力的情况, 在距桩体中心75∼325 mm 的6 个位置(间隔50 mm),深度150、250、350 和450 mm 处共设置了24 个微型土压力计.为了减轻自然光对图像质量的影响, 模型箱外部放置了2 个摄像灯, 从不同角度照射钢化玻璃.为了观察压桩过程中桩-土界面的剪切扰动区的情况, 在玻璃近表面处设置微距摄像头拍摄局部场.

图1 模型装置Fig.1 Model test setup

1.2 土样性质与制备

试验所用的材料是自然干燥的建筑黄砂, 其基本性质见表1.

表1 砂土的基本性质Table 1 Basic properties of sand

为了保证每次试验的密实度相似, 使用标准化程序制备砂.同时, 为了方便埋置土压力计,在模型箱中分5 层铺设干砂, 铺设高度依次为350、100、100、100、150 mm.试验前, 预先将试验用的干砂全部放置于一大型塑料容器中, 随后根据各层铺设厚度计算出干砂在塑料容器中对应体积的高度, 并做好标记.制备土样的过程中, 将该塑料容器中对应高度的干砂, 采用雨落法逐层铺设到模型箱中, 严格控制好每层的体积和重量, 铺设完成后, 静置24 h, 让砂土在自重作用下压实.为了验证制备的砂体密度, 每次试验后都进行一次静力触探试验, 利用Mayne等[15]的方法估算相对密度, 经过比对后, 制备过程可达到较好的重复性.

1.3 图像及数据处理

DIC 是一种基于光学的不直接接触而检测物体变形的技术.本工作基于MATLAB 软件自行编制计算程序, 通过对桩侧土体位移采用无标示点方法进行连续采集, 实现对沉桩过程中桩周土体位移的动态分析, 并拟合土体的位移轨迹.相比较商业的PIV 系统, 本系统处理数据操作灵活, 可以计算并提取观察面所有位置任何时刻的水平及竖向位移, 也可导出矢量图和位移平均值.

试验得到的图像可以分成多个小的图像子集, 通过计算每个图像子集的位移最终获得整个图像的位移场.每个子集内的灰度值分布可以定义为一个函数f(i,j), 被拍摄对象变形或移动后的第二幅图像中对应子集的灰度分布函数为g(i+∆x,j+∆y).∆x和∆y表示为i和j的位移[16-17].采用MATLAB 图像匹配的标准相关函数为

在进行DIC 计算时, 位移场精确性不仅取决于图像质量, 还取决于像素子集[18].在反复计算并对比后, 本试验对于全场图像选取像素为12×12 的子集进行计算, 对于局部场图像,子集像素为24×24.另外, 为了通过图像的像素坐标推导出土颗粒的实际坐标[19], 每次试验前都需要进行标定.本工作中全场图像的标定系数为0.557 mm/pixel, 局部场的标定系数为0.013 mm/pixel.

2 试验结果与分析

2.1 全场位移

图2 为基于DIC 技术绘制的土体位移等值线图.图2(a)为压桩深度为450 mm(18R)时土体最终的水平位移云图, 正值表示向右位移,H为桩端的实际深度,r为距桩中心轴线的径向距离,Z为竖向深度(地表处为0),r和Z均按桩半径归一化、沉桩过程中, 土体受桩身的影响向两旁挤开.当桩被压到18R的位置时, 径向影响范围约为14R, 且随着压桩深度的增加, 影响范围也随之增大.图2(a)显示, 侧向土体位移场的影响范围可在桩端下延伸至大约0.5H的距离.图2(b)为桩深18R时土体的竖向位移等值线图, 正值表示向下位移.试验表明, 沿桩身的土的竖向位移可分为两个区, 其中一个区受桩端挤压作用, 土体向下移动;另一个区为桩身上半部的土体, 向上运动, 表明发生了土体隆起.总的来说, 水平和竖向土颗粒位移的轮廓与文献[20]中采用室内半模方桩试验观察到的轮廓相似, 但本工作中图像记录的数据范围更大,边界效应的影响更小.图2(c)为在水平位移和竖向位移的基础上合成的位移矢量图, 其中每个向量表示在大约28 mm×28 mm 的区域内发生的位移.图2(c)清晰地显示了桩端在18R深度时土体最终位移的上升和下降趋势.

图2 H =18R 时的土体位移云图和矢量图Fig.2 Contour maps and vector maps of soil displacements when H =18R

2.2 桩周土体累计位移

图3 为不同径向距离处的土体随压桩深入而产生的累计水平位移, 规定向右移动为正.由图3 可知: 不同径向距离处土体的位移变化规律大致相同, 都经历了一个由缓慢增加至稳定的过程, 当某一测点的位移达到稳定状态时, 桩端深度均超过测点深度.这与罗战友等[3]通过现场试验实测发现最大水平挤土位移与压桩深度存在着滞后效应的现象一致, 即压桩深度达到某一位置点时, 这一位置的水平位移还未达到最大值, 而是当压桩深度超过这一位置时才达到最大值, 且在随后的压桩过程中最大值基本保持恒定.对比不同位置的测点发现: 距离桩体越远, 土体的水平累计位移的最大值越小;深处土体的位移比浅处土体稳定得更慢, 其最大值也更大.

图3 各深度处不同径向距离测点的水平累计位移Fig.3 Horizontal cumulative displacement of measuring points with different radial distances at different depths

图4 为不同径向距离处随桩体的深入而产生的累计竖向位移变化过程.由图4 可知: 与水平累计位移规律相似, 不同径向距离测点处的竖向累计位移随着沉桩深度的增加逐渐达到稳定状态, 距离桩体较远的测点位移总比距离桩体较近的位移小;与累计水平位移不同, 随着压桩的进行, 较深处的土体的位移模式是先向下运动, 随后向上运动, 且变化在桩端位于测点深度上方约2R时便发生了, 而Z=6R处的土体由于深度较浅, 向下运动的位移不明显.

图4 各深度处不同径向距离测点的竖向累计位移Fig.4 Vertical cumulative displacement of measuring points with different radial distances at different depths

2.3 桩周土体最终位移

试验过程中, 桩体共压入450 mm(18R).图5 为压桩深度为18R时, 距桩体中心不同径向距离的土体最终水平位移.由图5 可知: 土体水平位移最大值约在深度16R处, 即桩端深度上方约2R处;上半部分土体水平最终位移沿深度的增加而增加, 当土体深度超过16R时, 最终位移沿深度的增加而减小, 且随着径向距离的增加, 最终水平位移在逐渐减少.例如:r= 3R位置土体的水平位移最大值为3.8 mm, 约为桩径的7.6%;r=5R位置土体的水平位移最大值为3 mm, 约为桩径的6%;r=7R处最大值为2.3 mm, 约为桩径的4.6%.

图5 H =18R 时不同径向距离土体的最终水平位移对比图Fig.5 Horizontal displacement at different radial distance

图6 为压桩结束时距离地表不同深度处土体的竖向位移图.由图6 可知, 距离桩体中心越远, 土体的竖向位移量越小.Z=0、6R和10R深度处的土体最终向上移, 其中Z=0 处土体隆起, 位移最大值在桩土界面处, 约为2.5 mm, 与Z= 6R处土体的竖向位移大小相当, 但在Z= 6R处,r= 3R到10R范围内的土体竖向位移更大.Z= 14R和Z= 18R处土体向下移动, 其中Z= 18R处土体的径向影响范围最大, 约为7R.向上运动和向下运动的分界线约为Z=12R处(见图2(b)), 约为压桩深度的2/3.

图6 H =18R 时不同深度土体的最终竖向位移Fig.6 Comparative of Vertical displacement at different depth

观察Z= 10R和Z= 14R处位移曲线的趋势可以看出, 土体的竖向位移有曲折的表现,结合试验过程中不同时间点的云图分析, 原因是桩体在贯入初期, 土体的运动趋势向下, 随着压桩深度的增加, 土体的运动方向改为向上运动, 于是发生了曲线的转折, 根据曲线的转折位置可以判断运动方向改变最剧烈的范围主要在集中在距离桩中心1R ∼3R的范围内.

2.4 桩周土压力与土体位移

试验过程中, 土中不同深度和不同径向距离处铺设了微型土压力传感器, 用以研究静压沉桩过程对周围土体的挤压效应.土压力计是侧向埋设, 测得的皆为水平土压力, 并且只记录试验过程中的土压力增量.图7 为沉桩过程中侧向土压力增量的峰值在不同深度处沿径向衰减变化.可以看出, 在沉桩过程中, 同一深度下, 距离桩体较近的土体受沉桩挤压作用影响更大.同时, 在同一径向距离下, 深层土体的土压力受沉桩影响更大, 这一方面是由于深层土体较浅层土体更为密实, 另一方面是由于深层土体处于较高的自重应力水平, 所以桩体贯入时土体的挤压效应也更明显.

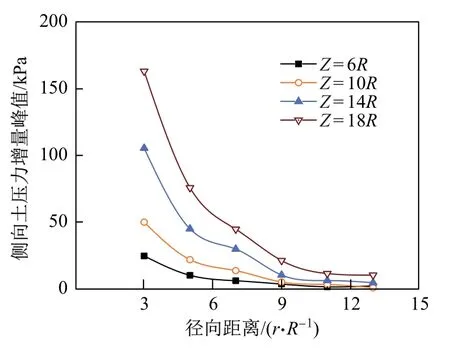
图7 不同深度桩侧向土压力峰值沿径向距离变化Fig.7 Peak value of stress increment with radial variation at different depth

侧向土压力受到径向距离和深度变化的影响, 这一点与之前提到的土体位移变化情况相似.本工作将土压力增量与土体累计位移变化过程联合分析.图8(a)展示了径向距离r= 5R处不同深度下土体随桩体的压入而产生的水平应力增量的变化过程.可以看出, 在不同的深度, 随着桩端逐渐靠近测点, 应力增量也达到最大.桩端通过后, 应力增量逐渐减少.值得注意的是, 在桩端达到测点深度之前, 测得的水平应力增量已经达到峰值.这种现象可以称为“提前”效应, 这与Jardine 等[5]的观察结果一致.图8(b)是径向距离5R处不同深度土体随桩体压入而产生的的累计水平位移变化过程, 可以看到, 在压桩开始后, 水平位移先逐渐增大,随后趋于稳定.比较图8(a)和(b)可以发现, 当土颗粒间存在应力时, 土体位移逐渐增大, 在土颗粒间应力消散时土体位移趋于稳定.图8(c)给出了相应位置的累计竖向位移的变化过程.压桩过程中, 除了较浅处的土体, 其他测点处土体先向下移动, 后向上移动.对比图8(a)和(c)可以发现, 当侧向应力增量降至0 时, 累积竖向位移几乎也是达到稳定值.值得注意的是, 当土体位移模式从向下运动转换为向上运动时, 对应时刻的应力增量几乎同时达到峰值, 这说明土颗粒竖向运动模式发生改变往往是在该处土压力达到最大值的时刻.

图8 r =5R 侧向土压力增量和相应位置测点累计位移Fig.8 Horizontal stress increment and corresponding accumulative soil displacements when r =5R

2.5 桩-土界面剪切扰动区

在全场位移分析中, 每幅图像需要覆盖的范围较大, 而相机分辨率是一定的, 故牺牲了桩-土界面土体位移的图像捕捉.因此, 试验过程中安装了一个额外的微距摄像头捕捉桩-土界面土颗粒位移在压桩过程中的变化情况, 从而实现对剪切扰动区厚度的测量.微距摄像头位置在距砂土地表100 mm 深度处(见图1).图9(a)为微距摄像头拍的照片, 试验过程中为了方便观察和验证, 放置了一部分与砂子性质相似的白砂.图9(b)为桩体刚通过观察区域, 用DIC 计算的间隔为2 mm 的砂土矢量位移图.可以看到靠近桩体的一侧有明显的一段位移.当桩与土体发生相对位移时, 距桩身较近的土颗粒在桩体带动下发生明显的平动和转动, 距桩身越近,土颗粒的变位就越大.通过原始照片和DIC 计算的结果可以基本判断出, 剪切扰动区的厚度为2∼3 mm 左右, 即D50的5.7∼8.6 倍.对桩体穿过后的图像也进行了分析, 整个扰动区表现为竖直下移, 并且当桩体穿过后, 扰动区的位移量会减小.

图9 桩-土界面土体位移情况Fig.9 Soil displacement of pile-soil interface

部分学者研制了配合PIV(或DIC)技术的加载剪切仪, 通过界面剪切试验模拟分析结构物附近的颗粒运动, 这与实际的压桩试验不完全相同, 但也能一定程度上反映桩体的移动带动土颗粒位移的影响.Dejong 等[13]的研究中, 距结构面5∼7 倍粒径处, 土颗粒的位移和转角已变得很小, 张嘎等[14]认为接触面剪切引起的土颗粒变位大约局限在距结构面5∼6 倍平均粒径的范围内.这些研究与本工作扰动区厚度的5.7∼8.6 倍平均粒径大致吻合.

事实上, 桩身表面的粗糙程度会对扰动区的形成产生影响, 本试验中使用的是铝合金材料桩, 这与粗糙表面的实际桩有区别.不仅如此, 扰动区还与土的颗粒级配、土颗粒的摩擦角、压桩速度等因素有关, 因此, 未来对扰动区的研究还有很多因素和工况要考虑.本工作提出的通过设置局部微距摄像头并进行DIC 计算的方法, 可以很好地观察扰动区地厚度和位移.具体的不同颗粒级配、不同粗糙程度等影响还需在进一步的研究中继续考虑.

3 结 论

数字图像相关技术作为一种非接触技术, 可用于桩模型试验中获取任意时刻任意位置的土体位移, 并且可以通过云图或者矢量图的方式清晰地呈现整个位移场.本工作应用DIC 技术进行了静压沉桩全场和局部场的位移计算, 得到如下结论.

(1) 土体的水平位移随桩体的压入先逐渐增大, 后趋于稳定, 较深处土体水平位移的稳定值更大.压桩结束后, 水平位移的最大值在桩端上方2R处左右.竖向位移方面, 土颗粒随着桩体的压入经历一个先向下后向上运动的过程, 因深度的不同而产生不同方向的最终位移.压桩结束后, 以桩深的2/3 为界, 上部土体的最终位移向上, 下部最终位移向下.

(2) 桩体压入过程中, 侧向土体应力变化过程具有“提前”效应: 某深度处土体应力在桩尖到达前已经达到峰值.然而, 随着土体径向距离的增加, 该效应不再明显.同时, 土体应力与水平和垂直位移同时存在对应关系.当土体应力达到最大值时, 该处土体竖向位移模式发生改变.

(3) 桩土界面剪切扰动区厚度约为5.7∼8.6 倍平均粒径, 与文献研究结果吻合较好.扰动区主要表现为垂直下移, 当桩体穿过后, 位移会逐渐减小.局部摄像头的设置为观察扰动区的运动模式提供了良好的参考.