四轮独立驱动电动车自适应巡航滑模控制

周 苏，陆一弘，吴 楠，金 杰

(1.同济大学 汽车学院，上海 201804；2.同济大学 中德学院，上海 201804)

随着用户对汽车安全性、舒适性要求的不断提高，涉及汽车纵向动力学控制的研发也日趋广泛和深入，诸如巡航控制、防抱死制动、电子驻车制动等相关功能的实现已是现代汽车产品的基本元素。其中，基于雷达和摄像头的自适应巡航控制（Adaptive Cruise Control，ACC）是智能辅助驾驶研发的重要内容之一[1]。ACC 系统可以在一定程度上提高行驶安全性，降低驾驶员疲劳强度。

针对ACC 系统的控制方法，国内外已有众多专家和学者进行了研究，典型的控制算法有PID 控制、最优控制、神经网络控制与模型预测控制等。这些控制方法已取得了阶段性进展，目前一些汽车公司的高档轿车上已经配备了ACC 系统[2]。

然而，ACC 的研究对象以往多局限于传统的内燃机汽车。例如，李以农等[3]基于模糊逻辑和滑模控制理论，通过对节气门开度和制动压力进行协调控制，使智能车辆能准确跟踪期望加速度。王秋[4]基于模型预测控制同时兼顾车辆行驶过程中的多个目标对控制器进行设计，采用的逆动力学模型以内燃机的特性为基础。

对于电动汽车，因其纵向动力学特性、驱动/制动方式与传统内燃机汽车不同，ACC 策略及实现方式也会有所不同。LUO Yugong 等[5]对混合动力的ACC 系统进行了研究，应用模型预测控制方法所设计的控制系统，使车辆在燃油效率与跟踪性能之间达到协调，研究对象的动力系统包括内燃机和电机。赵立娜[6]采用分工况、分层的策略对电动汽车的ACC 系统进行控制算法研究，研究对象的动力系统为集中式电机。

可见，目前应用于四轮独立驱动电动汽车ACC算法的研究较少，因此，有必要开展针对性研究。本文基于研制的四轮独立驱动电动汽车平台，详细推导了基于趋近律的ACC 上位控制器滑模鲁棒控制模型；下位控制器根据动力学原理计算给出轮毂电机的期望转矩输出；在CarSim 中建立了电动汽车整车模型并选取典型工况后，进行了嵌入ACC功能模块的CarSim/Simulink 联合仿真计算，对ACC 控制策略进行仿真验证。

1 四轮独立驱动电动汽车平台及车辆参数

一款平台采用4 个轮毂电机独立驱动方式的电动汽车如图1 所示。这种电机与轮胎集成一体的设计省去了离合器、变速器、差速器和传动轴等传统汽车的部件，不仅降低了结构复杂度，还减轻了整车质量并增大了可用空间。同时，相比传统车辆，四轮独立驱动电动汽车具有更多的可控自由度，可以实现传统汽车无法完成的原地转向、斜行以及侧行等特殊功能，从而提高行驶机动性。当采取前后轮同时转向策略时，该电动汽车在给定参考路径下具有较优的跟踪性能[7]。以上述四轮独立驱动电动汽车平台的数据（表1）为基础来开展ACC 的仿真研究。

图1 四轮独立驱动电动汽车

表1 车辆模型及空气动力学部分参数

2 ACC 系统设计

2.1 ACC 系统结构

ACC 系统的基本功能是使行驶车辆（主车）与前方车辆（前车）保持一定的安全距离，保证行驶安全，减轻驾驶疲劳。ACC 系统的结构如图2 所示，其被控对象包括主车和前车的行驶轨迹，执行器为4 个轮毂电机，控制器分为上位控制器与下位控制器。为研究方便，把下位控制器、电机、主车与前车的行驶轨迹定义为ACC 系统的广义被控对象。

图2 自适应巡航控制系统结构示意图

根据主车车速，设定主车与前车的期望车距；上位控制器根据期望车距、主车车速，以及在主车上搭载的雷达/摄像头等设备对前车感知的参数，按照某一控制规律计算得到主车的期望加速度，作为广义被控对象的输入信号；下位控制器根据期望加速度，计算得到各轮毂电机的期望输出转矩；轮毂电机根据期望转矩，输出实际转矩；主车在电机的4 个实际转矩作用下行驶。要实现以上ACC 功能，上位控制器的控制规律至关重要。

2.2 期望车距设定

为了上位控制器能够给出合理的期望加速度，保证自适应巡航安全，必须由上一层的整车控制器设定主车与前车之间的期望距离。目前，固定时距策略是一种广泛采用的方法[8]。所谓时距，是指主车按当前车速行驶到前车位置所需的时长。该方法中，期望车距设定为随主车车速线性变化。

式中：Tv为时距，s；L0为主车静止时两车之间的最小距离，m；vr为主车行驶速度，m/s。

2.3 广义被控对象模型

将上位控制器输出主车的期望加速度用作广义被控对象的控制信号（输入信号）。如2.1 节所述，ACC 系统的广义被控对象由下位控制器、电机、主车与前车的行驶动力学系统（行驶轨迹）构成。

2.3.1 下位控制器模型

下位控制器的功能是将上位控制器给出的期望加速度转化为各轮毂电机的期望转矩。

直线行驶时汽车纵向上受驱动力和行驶阻力作用。行驶阻力包括滚动阻力、空气阻力、加速阻力和坡度阻力。假定路面附着条件理想，主车每个车轮的驱动力可以等效为：

式中：Ti为每个轮毂电机的输出转矩，下标i为左前轮、右前轮、左后轮、右后轮；r为车轮半径；Fti为每个车轮的驱动力，下标t为驱动力。

不考虑坡道行驶工况，主车行驶时应当满足：

式中：ΣTi为轮1毂电机2期望输出转矩之和；CD为空气阻力系数；A为迎风面积，m2；A ρ为空气密度，kg/m3；f为滚动阻力系数；m为整车质量，kg；ades为主车的期望加速度，m/s2。

实际行驶时阻力系数通常无法精确获取，因此，将中型车典型的空气阻力系数以及良好沥青路面的滚动阻力系数（表2）用于下位控制器设计。

表2 阻力系数估计参数

下位控制器根据上位控制器输出的期望加速度和实测的主车车速，按式（3）计算得到轮毂电机期望输出转矩之和ΣTi。

直线行驶时，各轮毂电机的期望输出转矩相同，即：

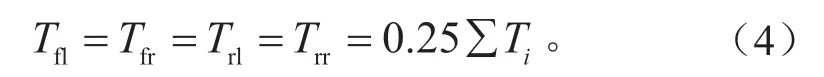
式中：fl、fr、rl、rr 分别为左前轮、右前轮、左后轮、右后轮。

转向时，为使车辆的横摆角速度迅速响应，采用增加一侧电机期望转矩、减少另一侧电机期望转矩的方法。汽车转向时的稳态横摆角速度wc为：

式中：δ为前轮转角，rad；L为轴距，m；K为稳定性因数（按中型车典型参数，取值0.002 s2/m2）。同侧电机的期望转矩取值相同，根据稳态横摆角速度wc与车辆实际横摆角速度w（由传感器测得）的偏差对各个电机的期望转矩进行比例调节，即：

式中：k为比例系数（根据经验取10）。

下位控制器按式（4）或式（6）～（7）同时输出4 个轮毂电机的期望转矩Ti至电机（包括电机控制器）。

2.3.2 电机模型

采用的4 个轮毂电机为同一型号，其最大功率为Pmax=7.5 kW，最大转矩为Tmax=150 Nm。电机在低速区间恒转矩运行，在高速区间恒功率运行。电机峰值转矩（绝对值）Tm的计算公式为：

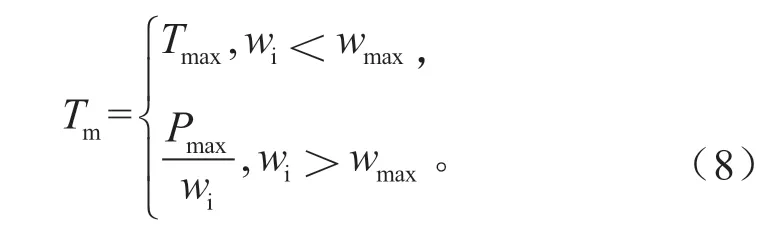
式中：wi为电机旋转角速度，rad/s；wmax为电机峰值转矩对应的最大角速度，即wmax=Pmax/Tmax。

式中：τ为电机动态时间常数（根据实测取20 ms）。

2.3.3 主车动力学模型

主车实际的加速度ar满足：

式中：f ′、分别为主车实际的滚动阻力系数和空气阻力系数。

2.3.4 包括前车行驶状态的广义被控对象模型

首先考虑如图3 所示的直线行驶情形。该坐标系中，主车与前车均沿x轴正方向行驶，主车前部和前车后部的绝对坐标分别为lr和lf。选取两车的相对距离及其导数（相对速度）为状态变量，即：

式中：为前车加速度，即干扰量。

并定义广义被控对象的输出变量：

式中：c 为常数，大于0。

图3 自适应巡航控制示意图

考虑式（10）、式（11）和式（12），广义被控对象可用以下状态方程形式描述。

式（9）中电机动态过程较状态变量x1和x2的动态过程要快很多，可以近似认为则广义被控对象的状态方程表达式为：

2.4 ACC 上位控制器设计

ACC 上位控制器的功能是给出主车在当前状态下的期望加速度u。ACC 系统[式（14）]是一个非线性时变系统，采用传统的PID 控制会导致车辆的实际加速度出现较大的超调[1]。因此，上位控制器采用基于趋近律的滑模鲁棒控制。

根据式（1）得到的期望车距Ldes，ACC 系统[式（14）]的期望输出为：

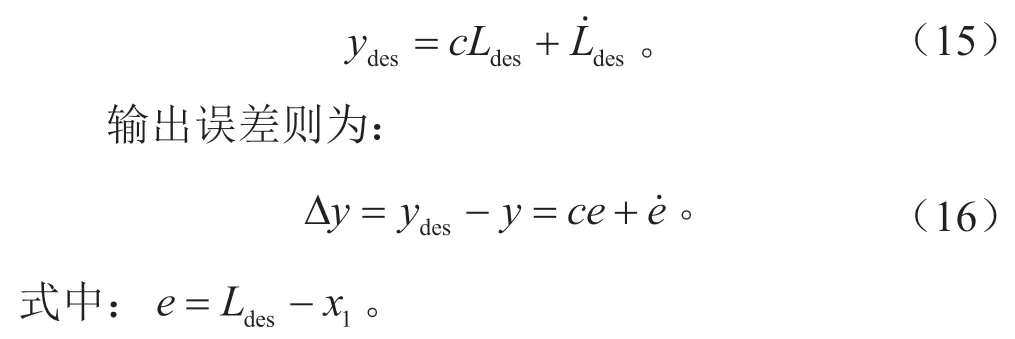
ACC 系统的控制功能是，使主车与前车的相对距离尽快趋向于期望车距，即；使主车与前车的相对速度为0，即。为了满足这两点功能，构造滑模切换函数[10]公式为：

并采用指数趋近律的控制目标公式为：

考虑到

联立式（14）、（18）和（19）可得控制律公式为：

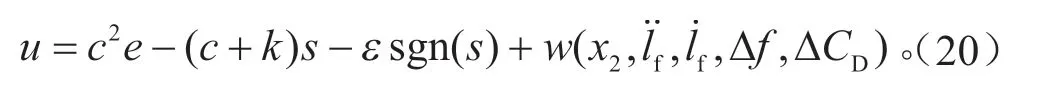
式中：c、k和ε为控制参数，可根据实际经验或控制性能指标需求选取；e和s分别为控制误差及滑模切换函数，可以通过在主车上搭载的雷达/摄像头等设备、车速传感器或状态估计等实时获取；w为不可操纵的干扰变量。

为了解决干扰变量w未知这一问题，同时保证系统的稳定性，根据干扰的上下界区间来设计控制律。不妨用待设计的wd来代替式（20）中的干扰变量w。控制律改写为：

联立式（14）、式（19）、式（21），得到：

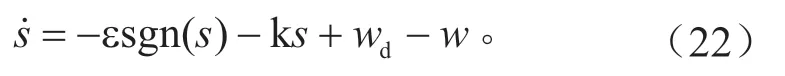
式中：wd为待设计的干扰变量。

记wL与wU为干扰的下界与上界，即wL≤w≤wU，可以通过选取wd满足，从而保证存在滑动模态以及满足到达条件，即系统的误差相轨迹在有效时间内到达切换面。

根据式（22），当s＜0 时，wd=wL⇒则；当s＜0 时，wd=wU⇒因此，取

此外，为了减轻滑模控制系统固有的抖振，在滑模面附近设计边界层，即用饱和函数sat(s)

代替符号函数sgn(s)[6]。其中，Δ为边界层的厚度，根据经验取0.5。

综上所述，得到ACC 滑模控制律公式为：

对于车辆在弯道行驶的情形，在某一时刻，主车所在位置的大地坐标为（pr,qr），前车所在位置的大地坐标为（pf,qf）。两车的相对距离d用直线代替曲线，即为：

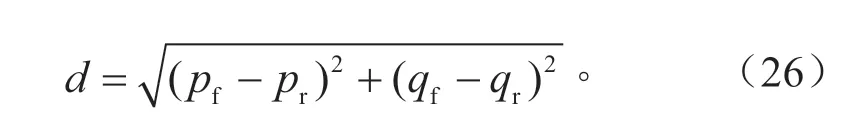
考虑到主车车速可以通过传感器得到，结合d对时间的导数即可得到前车速度的测量值。因此，应用于直线的ACC 滑模控制律[式（25）]同样适用于弯道行驶情形，上位控制器无需知道主车与前车的大地坐标即可控制（只需两车的相对距离）。

2.5 车轮转角控制器设计

车辆在直线行驶时，车轮转角均为0。车轮转角无需进行控制。

车辆在弯道行驶时，车辆按照期望的路径行驶是保证ACC 系统能够顺利工作的前提。为了模拟驾驶员操纵方向盘沿期望路径行驶的行为，以当前车辆位置与期望路径的垂直距离作为偏差输入，前轮转角作为系统输出，采用PI 控制算法。设垂直距离为v(m)，前轮转角输出为θ(rad)，则PI 控制律为：

式中：Kp为比例系数，根据整定选取100；Ti为积分时间常数，根据整定选取50。

3 CarSim/Simulink 联合仿真

采用CarSim/Simulink 联合仿真的方式，验证式（25）描述的ACC 滑模控制律。Simulink 实现前车运动模型、上位控制器、下位控制器、电机模块、转角控制器等模块，CarSim 实现主车运动模型。在CarSim 环境下，选取B 型车为主车。B 型车在CarSim 中默认为内燃机车，因此，为实现电动汽车整车动力学模型，需要对原整车模型中的动力总成模块进行更改[11-12]。将“Powertrain”（动力总成）的选项更改为“4-wheel drive”（四轮驱动），同时在相关选项中选择“No dataset select”（无数据选取）。将四轮驱动的转矩直接作为车辆模型的输入量，Simulink 实现的电机模块提供这4 个转矩输入量。此外，4 个车轮的转角输入也由Simulink 实现的转角控制器提供。其余的主车模型参数按照表1 的数据选取。

CarSim 把主车行驶速度、横纵向位移量输出给上位控制器模块；把4 个车轮纵向转动角速度输出给电机模块；把横摆角速度输出给下位控制器模块。

CarSim/Simulink 联合仿真模型最终搭建如图4所示，其中上位控制器延时为10 ms。

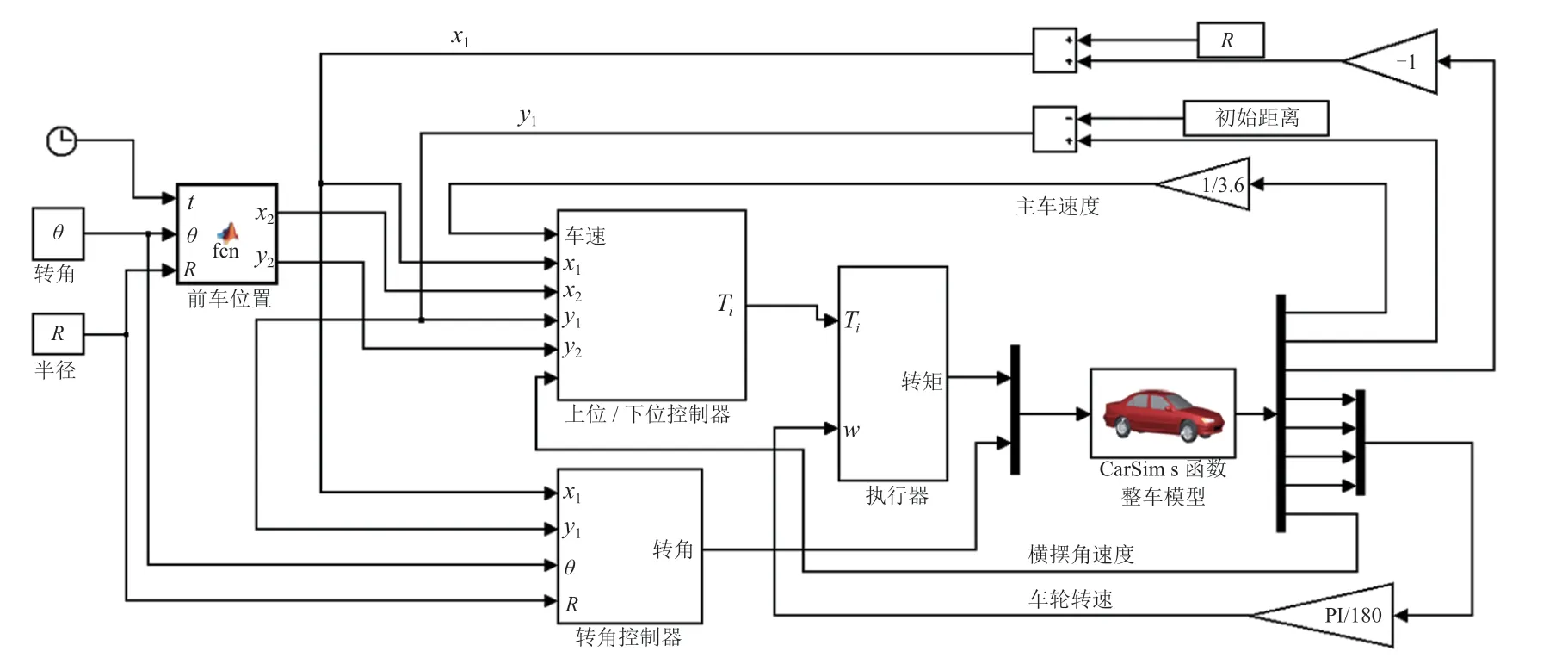
图4 CarSim/Simulink 联合仿真模型

4 仿真结果与分析

下面分别对直线行驶工况以及弯道行驶工况进行仿真验证。

4.1 直线行驶工况

仿真的相关参数设置为c=5，k=10，ε=5，wL=-3，wU=3，L0=3 m，Tv=1.5 s。

首先，验证控制算法的有效性。为了模拟前车在实际行驶中的各种工况，如匀速、加速、紧急制动等，前车在直线上按照如下规律运动（忽略加速度变化的时间）：0～10 s 以40 km/h 的速度匀速行驶；10～15 s 从40 km/h 匀加速到60 km/h；15～25 s 以60 km/h 的速度匀速行驶；25～30 s 从60 km/h匀加速到80 km/h；30～40 s 以80 km/h 的速度匀速行驶；40～45 s 从80 km/h 匀减速到20 km/h；45～60 s以20 km/h 的速度匀速行驶。初始时刻主车速度为30 km/h，前车速度为40 km/h，两车相对距离为20 m。

直线行驶工况的仿真结果如图5～8 所示。

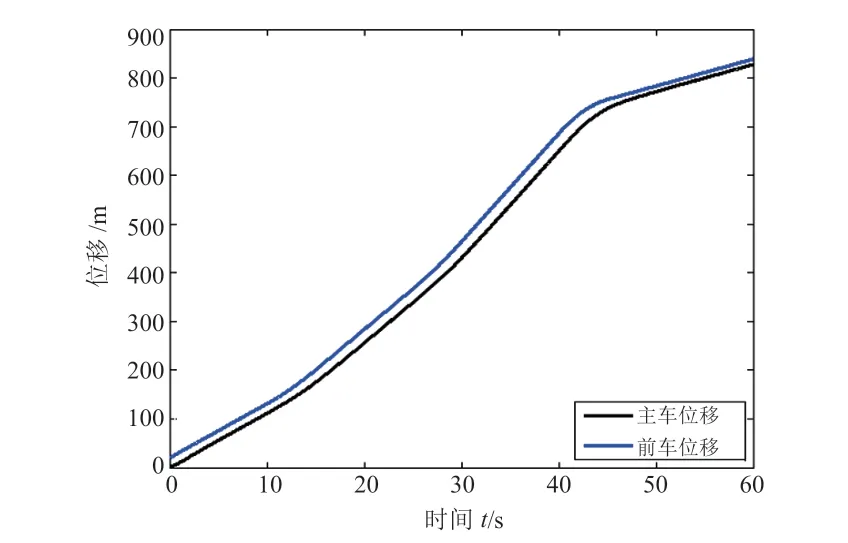
图5 主车与前车的位移对比

图8 实际车距与期望车距的误差曲线

由图5 可知，在整个仿真过程中，主车始终能跟随前车，并保持一定车距。当车速较快时，车距相对较大；当车速较慢时，车距相对较小。

由图6 可知，主车的初速度（30 km/h）低于前车的速度（40 km/h），因此，主车速度迅速增大直到与前车速度一致，且超调不明显。随后，当前车处于加速、匀速、减速等各种行驶工况时，主车的速度都能较快地跟踪前车速度，并且几乎没有超调。

由图7 可知，初始时为使主车速度迅速增大，所以主车的加速度较大。待主车速度与前车一致，且两车保持到期望车距后，主车的加速度能够跟随前车的加速度。在40～45 s 时，由于受到执行器电机功率的限制，加速度的响应时间稍长，但跟踪的效果依旧较好。

由图8 可知，初始时由于两车车速不一致以及初始车距与期望车距不同，车距有相对较大的误差。随后距离误差迅速减小，除在45 s 左右（由于减速度限制）外，误差始终保持在0.3 m 以内。

其次，验证控制算法的鲁棒性。实际行驶时滚动阻力系数、空气阻力系数与下位控制器设计的参数存在偏差。为验证模型偏差对控制效果的影响，选取以下3 组下位控制器参数进行仿真：①f=0.009，CD=0.142；②f=0.018，CD=0.284；③f=0.027，CD=0.426。初始时刻主车速度为30 km/h，两车相对距离为20 m，前车速度恒定为40 km/h。

图9 不同下位控制器参数的速度对比

由图9 可知，在实际阻力系数未知的情况下，不同下位控制器的参数均能达到良好的控制效果。在阻力估计低估与高估较多的情况下，主车速度仅在峰值附近产生大约1%的差异，随后均迅速收敛到期望值附近。

4.2 弯道行驶工况

车辆在弯道行驶时，为保证行车安全，仿真的相关参数设置为：c=5，k=10，ε=5，wL=-3，wU=3，L0=5 m，Tv=2 s。

车辆在弯道行驶时，智能设备测得的两车相对距离是直线距离，以此代替实际行驶中的曲线距离。因此，当道路的曲率较小时，直线距离与曲线距离误差较小，对控制效果的影响不明显；当道路曲率较大时，直线距离与曲线距离有较大误差，从而造成前车速度的测量值与实际值产生一定的偏差，对主车的速度控制效果产生一定的影响。

图10 车辆弯道行驶示意图

为了便于研究，选取如图10 所示曲率较大的道路：BC 段为曲率半径为R=50 m，圆心角α=90°的圆弧；AB 段与CD 段均为直线，与BC 段相切。主车在初始时刻位于A 点，车速为40 km/h，沿方向A →B 行驶；前车在初始时刻位于B 点，车速为30 km/h，假定沿方向B →C →D 匀速率行驶。初始时主车与前车的相对距离AB=30 m，期望主车沿A →B →C →D 行驶。

图11～13 是弯道行驶工况的仿真结果。

图11 前车实际速度与测量速度对比

图12 主车速度变化曲线

图13 直线车距变化曲线

由图11 可知，虽然前车一直以30 km/h 的速度行驶，但通过智能设备计算得到的前车速度却存在一定的波动。约0～3 s 时，由于主车沿直线AB行驶，前车沿曲线BC 行驶，两车之间直线距离的变化率小于实际两车的速率之差，在主车速度已知的情况下，测得的前车速度会偏小；约3～9 s 时，由于主车沿曲线BC 行驶，为保证横向的稳定，自身的车速会引起一定范围内的波动，测得的前车速度会引起小幅振荡；约9～12 s 时，由于主车沿曲线BC 行驶，前车进入直线CD 段，两车之间直线距离的变化率大于实际两车的速率之差，在主车速度已知的情况下，测得的前车速度会偏大。约12 s后，两车均进入CD 段，测得的前车速度与实际值一致。仿真过程中，前车速度的测量误差大约在1 km/h，即实际车速的3.4%左右，能够满足控制要求。

由图12 可知，初始时主车速度为40 km/h，由于两车的相对距离稍大，所以主车短暂加速。随后主车速度迅速接近前车速度，即减至大约30 km/h。主车跟随的是前车速度，而前车速度的测量值仅在30 km/h 附近小幅波动，所以对于主车40 km/h 的初始速度而言，前车速度的波动对两车的相对速度影响有限，即使是弯道工况，主车仍旧能够较快地接近前车速度。当然由于前车速度的测量值有一定的波动，主车速度也会有小幅度的波动（如约11 s附近），但控制的总体效果依旧较好。同样，图13中的直线车距也因前车速度测量值的波动产生小幅度的波动，在初始条件存在误差的情况下，最终仍旧能够较好地收敛到期望车距附近。

5 结论

（1）基于CarSim/Simulink 联合仿真搭建的四轮独立驱动电动汽车的模型，能较好地仿真车辆动力学特性，满足电动汽车ACC 的仿真要求。

（2）直线行驶工况仿真结果表明，采用本文基于滑模鲁棒控制的ACC 算法，能够使主车快速、准确地跟踪前车的速度，并使两车距离保持在期望值附近，有着良好的控制效果。

（3）弯道行驶工况仿真结果表明，在曲率较大的道路行驶时，前车速度的测量误差控制在一定范围内，本文采用的ACC 算法能够在弯道行驶时依旧有着良好的控制效果。

（4）对车距的准确测量是本文ACC 工作的前提。在此基础上，该算法能够满足电动汽车ACC系统对安全性、鲁棒性的要求。