基于多传感信息融合的智能车辆定位方法

赵一兵，刘昌华，郑 震，郭 烈，马振强，韩治中

(大连理工大学汽车工程学院，辽宁，大连 116024)

高精度的定位系统是智能车辆感知层的重要一环，它解决行驶过程中“我在哪里？”的问题，是实现智能车辆自主导航的基础[1]。根据智能车辆对周围环境的感知程度分为绝对定位和相对定位[2]。在进行相对定位时，基于视觉定位的定位方式研究较为广泛，AZUMA[3]等利用扩展卡尔曼滤波算法将相机数据与IMU 数据相融合，结果表明，融合后的定位效果较好，能有效地减小系统误差。甘露[4]提出一种基于卷积神经网络的视觉定位系统，将双目视觉和卷积神经网络结合，定位效果稳定，具有较高的实用价值。

由于单传感器误差较大，将多个内部传感器数据相融合[5]的定位方式越来越得到专家学者的青睐。LIU 等[6]提出了一种基于1 个惯性测量单元和2 个3D 激光雷达的适合大型自然地形的实时6DSLAM 的方法，除了将整个地图划分为许多由大量基于树结构的体素组成的子地图之外，还使用概率方法来表示1 个体素被占用和空余的可能性，实时性得以提升。柯显信等[7]设计出包括红外定位系统、听觉定位系统和视觉定位系统的多传感器定位系统，提出的加权平均融合算法可使权重随目标位置和外部环境发生改变，环境适应性更强，有效提高了交互系统的整体定位精度和可靠性。

在静态环境下，基于地图匹配的定位方法经常取得不错的效果，该方法将传感器在一定范围内扫描得到的信息与先验地图的信息做匹配，得到符合度、一致性最好的匹配结果，从而确定智能车辆的位置，实现定位功能[8-9]。艾国[10]将地图匹配与激光陀螺惯性导航系统相结合，并提出基于曲线匹配的地图匹配方法，充分利用激光陀螺惯性导航系统的高精度姿态信息，较现有的点到点、点到线的匹配技术有更高的定位精度。李祎承等[11]提出了一种融合了视觉传感器和GPS/RTK 数据的视觉道路环境地图构建方法，在视觉地图的基础上，智能车仅需装载普通的摄像机和GPS 接收器便能实现高精度定位，有效降低了智能车成本。

1 智能车辆建模分析

试验所用智能车辆是锐趣科技的四轮小车平台，该平台基于ROS 操作系统，并采用四轮差速设计，同侧驱动轮以相同速度运行。激光雷达采用思岚A2 雷达，安装于小车顶部，驱动电机采用霍尔AB 型双通道的增量式光电编码器，惯性测量单元采用GY-85 九轴陀螺仪传感器。

将定位问题分为无地图定位与基于地图定位，通过理论与实践相结合的方式对智能车辆定位问题进行探索。试验结果表明，航迹推测法具有较明显的累计误差问题，不适用于长距离定位，基于地图的绝对定位方法对累计误差有一定校正作用，定位效果较为良好，说明了地图在定位系统中的重要性。

1.1 智能车辆运动学模型

试验基于室内结构化环境下完成，车轮厚度仅影响重心高度，且只考虑智能车辆车轮发生纯滚动情况，忽略车辆打滑，只建立其运动学模型，寻找状态变量与控制变量之间的函数关系。

将传感器坐标系与智能车辆坐标系合并，全局坐标系表示智能车辆的运动范围，局部坐标系建立在小车中心位置，用于确定环境中特征点相对于小车的位置分布。智能车辆的运动学模型如图1 所示。

图1 智能车辆运动学模型

在图1 中，坐标系xCOMy为局部坐标系，Xg0Yg为全局坐标系，用(x,y,θ)T表示智能车辆在全局坐标系中的位置和朝向信息，其中(x,y)表示智能车辆在全局坐标系中的坐标信息，θ表示在全局坐标系中的方向角。左右轮中心距离为2c，车轮的半径为R，智能车辆左右两轮的线速度分别为VL和VR，则智能车辆运动学方程可表示为：

且式(2)需要满足非完整性约束条件：

因此，可以通过调节左右轮的线速度来改变小车的位姿。

1.2 智能车辆传感器模型

1.2.1 里程计模型

假如在Δt时间段内，智能车辆的光电编码器的脉冲增量为ΔN，里程计分辨率为re，则小车在这段时间内移动的距离为：

若在这段时间内，小车左轮移动的距离用ΔdL表示，右轮移动的距离用ΔdR表示，令里程计模型的输入为u=[ΔD,Δθ]。其中，智能车辆对应的位移变化量ΔD与航向角变化量Δθ可以表示为：

根据智能车辆在行驶过程中航向角Δθ是否发生变化，可以把其里程计模型分为两种：直线模型和圆弧模型。在试验小车进行自定位的过程中，尽量增加采样频率，缩小初始点与终止点之间的距离，从而尽可能地保证定位过程的准确性。由于会频繁读取里程计的信息来获得智能车辆的位姿变化情况，因此，使用里程计的直线模型为主，在通过数据融合进行航向角计算时，需要使用圆弧模型。假设在t1时刻小车位姿为（x1,y1,θ1）T，在t2时刻小车位姿为（x2,y2,θ2）T，则表达式如下：

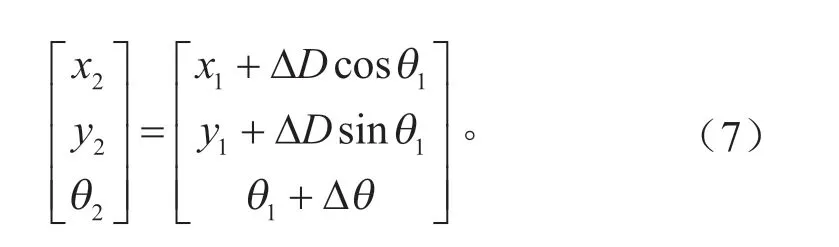
1.2.2 激光传感器模型

试验中忽略激光传感器自转时对不同角度的采样时间差，二维激光雷达的数据观测模型可以用条件概率进行表示：

式中：xk表示在k时刻智能车辆的位姿；zk表示激光观测量。由于激光传感器旋转一周会进行多次采样过程，由此可得：

假设激光传感器每次扫描得到的点之间相互独立，则对于每次完成一圈扫描得到的观测模型概率密度可以表示为：

1.2.3 惯性测量单元模型

惯性测量单元(IMU)具有灵敏、高频的特点，常作为其他传感器的辅助传感器使用，由物理理论可得：

式中：φ为旋转角度；v为小车速度；Δt为惯性测量单元相邻数据之间的时间差。

假设智能车辆的初始位置为p0=（0, 0,0）T，初始姿态为φ0=（0,0,0）T，R（φ0）表示初始姿态对应的旋转矩阵。欧拉角Δφ=（Δφx,Δφy,Δφz）T，欧拉角对应的旋转矩阵为R（Δφ）。

则进行多次迭代后，可以得出：

式中：ωk表示在k时刻IMU 所测量的角速度值。

利用加速度a和采样间隔时间Δt，可以得到在三维空间下智能车辆的速度和位移变化情况：

式中：ak表示在k时刻IMU 所测得的加速度值；Rk表示在k时刻时IMU 在世界坐标系下的姿态。

1.3 智能车辆定位问题建模

定位问题可以看作一个坐标系在另一个坐标系下的求解问题。假设智能车辆在全局坐标系中位姿为（x1,y1,θ1）T，在小车局部坐标系下任意一点的坐标为(x1,y1)，经过齐次坐标变换可以通过平移变换矩阵T，旋转变换矩阵R可转换至全局坐标系下，其中矩阵T和矩阵R为：

智能车辆的定位经常被称为位姿估计，而基于概率的状态估计是最常用手段[12]。概率运动学模型在定位过程中起着状态变换的作用，这即是条件密度，即：

式中：xt与xt-1表示智能车辆的位姿信息；ut表示运动控制，由里程计数据提供。这个模型表示在xt-1位姿基础上执行控制ut后，智能车辆取得的运动状态后验概率分布。

图2 智能车辆定位图例

定位图例如图2 所示，阴影节点值(地图m、测量值z和控制u)已知，时刻t的状态依赖t-1 时刻状态和控制ut，测量zt依赖t时刻状态。

2 智能车辆测量校准分析

智能车辆在硬件装配过程中会存在各种误差，从软件层面来说，系统在一定频率下接收数据，也会存在一定误差。因此，需要对智能车辆的IMU、线速度、角速度进行校准。

2.1 IMU 校准

在校准IMU 的过程中需对加速度计和陀螺仪分别进行校准，习惯上先对加速度计进行校准，然后利用校准后的加速度计信息来校准陀螺仪。加速度校准通常需将加速度计保持静止状态，根据测量值的二范数等于当地重力加速度来进行校准。陀螺仪校准过程主要包括Allan方差校准零偏噪声(Bias)和优化方式求解尺度因子及轴偏差[13-14]。

2.2 线速度、角速度校准

本文设计了线速度、角速度校准试验，在线速度校准中，通过校准文件使智能车辆前进1 m，将实际移动距离与理论移动距离(本文为1 m)的比值作为线速度修正系数，在角速度校准中，通过校准文件使智能车辆旋转360°，将实际旋转角度与理论旋转角度(本文为360°)的比值作为角速度修正系数。最后通过测程法前进返回试验对校准效果进行验证，共进行5 次试验，结果如图3 和图4 所示。

由图3 可知，校准后小车距离初始点的距离更近，其运动精度得到明显提高，通过对试验过程的观察以及对图4 中的数据结果进行分析可知，造成小车运动偏离的主要原因是旋转角度误差较大，通过校准后该问题得到显著改善。

图3 校准前后小车距原点距离对比

图4 校准前后小车航向角对比

3 无地图环境下智能车辆定位方法

3.1 扩展卡尔曼滤波

扩展卡尔曼滤波[15]是借助线性滤波理论求解非线性问题的算法，如果被用作多传感器的数据融合，可以将其中一个传感器数据当作测量量，另一传感器数据当作估计值进行融合。扩展卡尔曼滤波近似的主要思想就是线性化，最常通过泰勒展开进行线性化，然后对系统状态进行估计。扩展卡尔曼滤波分为时间更新方程和测量更新方程两部分，如图5 所示。

图5 扩展卡尔曼滤波算法流程

3.2 定位评价标准

定位评价标准是衡量一种定位算法好坏的指标[16]，本研究选用定位误差、定位成功率作为评价指标，其计算方式如下。

3.2.1 定位误差

定位误差指智能车的真实位置与估计位置之间的位置偏差，其表达式为：

式中：(xt,yt,zt)代表智能车辆通过定位算法估算出的位置；(xe,ye,ze)代表智能车辆在运动过程中的实际位置，由于智能车辆在室内结构化环境下运动，这里zt=ze=0，在实际计算时还要考虑小车航偏角偏差：

式中：θt代表定位算法估计出的航偏角；θe代表真实位置的航偏角。

3.2.2 定位成功率

在某一精度范围内，成功次数与总次数的比值，其表达式为：

3.2.3 定位实时性

指定位系统能否在规定时间内完成相应的逻辑处理并得到正确结果，实时性的高低是评价定位系统性能的重要指标。其影响因素包括硬件和软件两个层面。

3.3 多传感器融合定位试验

本文在robot_localization 功能包[17]的基础上进行改进，对里程计及IMU 进行数据融合，该功能包是所有状态估计节点的集合，每个状态估计节点通过其使用的传感器对小车在三维空间中的运动状态进行估计。在原功能包的基础上对其做了一些改进：

（1）修改了功能包中原有的参数配置读取功能，将里程计、IMU 等传感器相关模型及参数统一放置在参数配置文件中。根据小车实际的传感器参数进行配置，保证了功能包中的传感器模型与小车实际所用传感器的一致性。

（2）根据小车实际参数(传感器间外部参数、小车轴距、论据等参数)对小车进行了物理建模并将模型导入robot_localization 功能包，保证了小车实际尺寸与功能包中物理模型的一致性。

在robot_localization 功能包中，主要使用ekf_localization_node，该节点可以接收IMU 所测量的翻滚角、俯仰角、偏航角及速度和加速度，以及来自车轮编码器的偏航速度等。在ekf_localization_node 状态估计节点中，通常在只融合连续的位置数据(里程计、IMU)时，把世界坐标系和传感器坐标系设置为一个，此时世界坐标系为odom。多传感器融合下智能车辆TF 树如图6 所示。

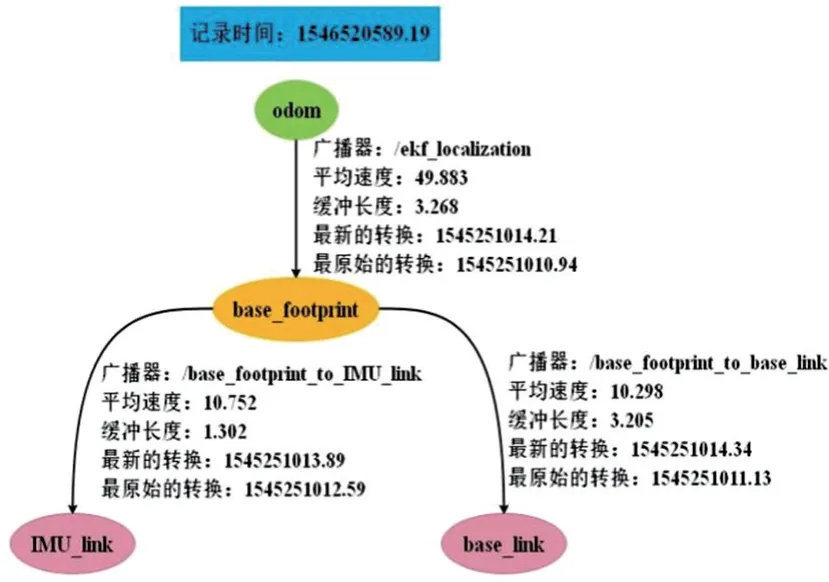
图6 多传感器信息融合下的TF 树

定位测试试验中经常使用的有两种方法：第1种是在实际环境中选取需要的定位点，让智能车辆重复到达定位点，比较智能车辆在定位点的输出值；第2 种是在实际环境下选取需要的定位点，让智能车辆重复到达定位点，比较小车定位点实际值与输出值。在无地图情况下定位试验采用第2 种测试方法。在该试验中共进行了直线轨迹与曲线轨迹两种试验，为降低由操作失误等不可控因素对试验结果的干扰，本文对试验结果根据格拉布斯(Grubbs)准则[18]进行了野值检测与剔除，处理后的结果如图7～10 所示。

图7 直线轨迹距离误差

图8 直线轨迹航向角误差

图9 曲线轨迹距离误差

图10 曲线轨迹航向角误差

由图7 和图9 可知，在无地图情况下通过航迹推测法进行定位存在较为明显的累积误差并会不断增加，不能通过外部传感器或先验地图信息进行修正，因此，在无地图情况下不做定位成功率评价。

在图8 和图10 中，角度误差均值分别为1.15°与3.25°，该结果可以反映在试验过程中小车按照既定轨迹行驶。

robot_localization 功能包是基于扩展卡尔曼滤波进行数据融合的，定位算法复杂度较低，实时性较好。在计算机上运行测试时，算法运行一次的时间稳定在10 ms 左右并且受计算机系统硬件因素影响。提高硬件系统配置可减少算法运行时间。

4 基于地图的智能车辆定位方法

4.1 环境地图构建

本文使用了ROS 开源社区中SLAM 算法——gmapping 功能包，该功能包订阅智能车辆深度信息、里程计信息和IMU 信息，同时需要完成相应参数配置，然后即可创建该环境下的二维栅格地图，如图11所示。

图11 试验环境地图

4.2 蒙特卡罗定位试验

蒙特卡罗算法[19]通过使用一系列带有权重的粒子模拟被估计状态的后验概率密度函数，又被称为粒子滤波[20]定位。粒子滤波器是贝叶斯估计器的一种实现方式，在处理非线性情况时具有天然优势，同时又能处理多峰分布情况。本文应用蒙特卡罗定位，定位方案如图12 所示。

图12 智能车辆定位方案

在定位过程中，智能车辆先从已知位置出发，首先利用内部传感器(里程计、IMU)获得自身状态信息，然后利用扩展卡尔曼滤波算法融合里程计和IMU 的信息，对小车的位姿进行一次粗略估计，再使用外部传感器(激光传感器)扫描周围环境，建立局部地图后，利用粒子滤波算法对小车位姿进行估计，从而获得智能车辆在全局中的位姿信息，其定位效果如图13 和图14 所示，图中绿色的点代表对智能车辆的位置估计，从图中可以看出粒子滤波能够有效地对智能车辆进行定位。

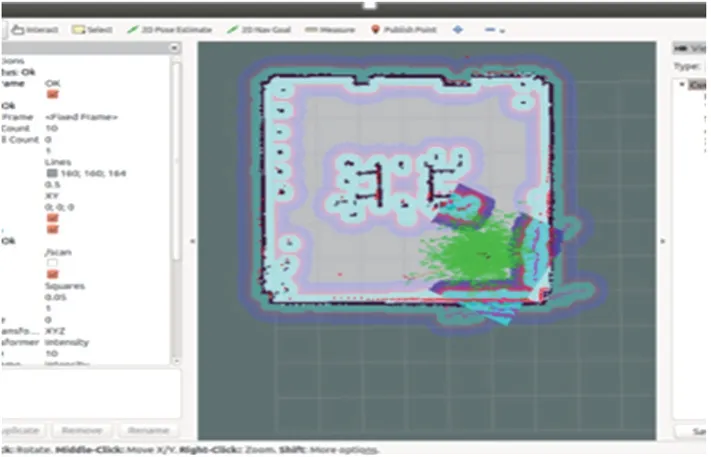
图13 粒子滤波前截图

图14 粒子滤波后截图

由于传感器精度有限，为了避免建图误差干扰，本次试验选取第1 种定位测试方式，同样进行了直线轨迹与曲线轨迹试验，并对试验结果进行野值检测与剔除，处理后的数据结果如图15～20 所示。

图15 直线轨迹距离误差

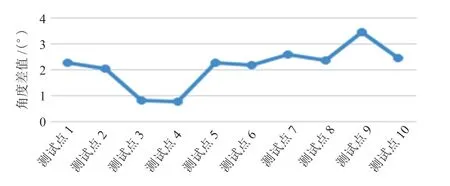
图16 直线轨迹航向角误差

图17 曲线轨迹距离误差

图18 曲线轨迹航向角误差

图19 直线轨迹位置误差结果

图20 直线轨迹航线角误差结果

图15 和图17 可知，定位误差存在不断累积增加的现象，但对比图7 和9 来看，距离误差有所减小，说明基于地图的定位效果比无地图定位有所提高。图16 和图20 中，航向角误差均值分别为2.12°和3.15°，对比图18 与图20 来看，航向角误差并无明显改善。

4.3 定位结果分析

根据定位评价标准对该试验结果进行分析。由图19 和图20 可知，在4 组测量共40 次定位结果中，出现了13 次不符合距离误差指标的定位结果，成功27 次，出现了4 次不符合角度误差指标的定位结果，成功36 次，可得直线轨迹定位成功率为：

由图21 和图22 可知，在4 组测量共50 次定位结果中，出现15 次不符合距离误差指标的定位结果，成功35 次，出现了13 次不符合角度误差指标的定位结果，成功37 次，可得曲线轨迹定位成功率为：

图21 曲线轨迹位置误差结果

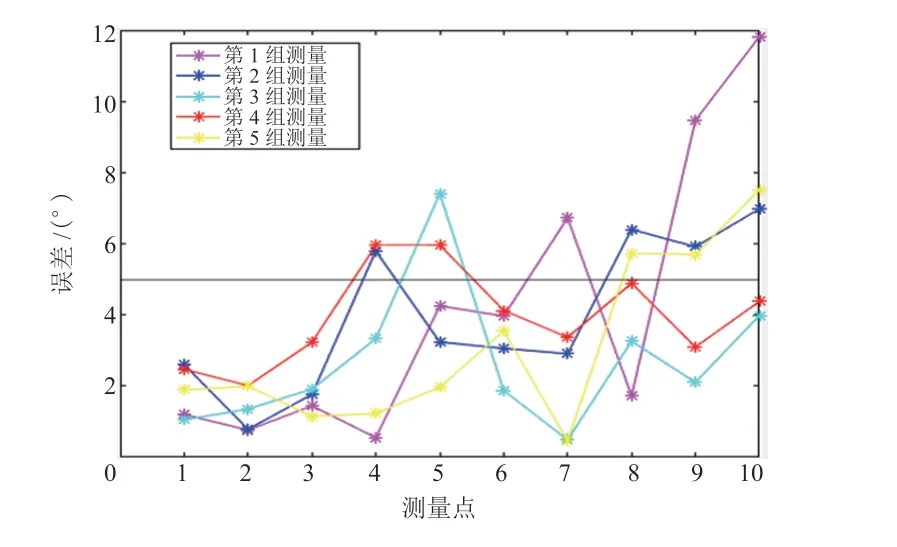
图22 曲线轨迹航向角误差结果

在定位的实时性方面，基于地图的定位采用蒙特卡罗定位算法，其本质是通过算法的迭代来逐步增加正确定位粒子的权重，忽略误定位粒子，进而实现准确定位。因此，在有地图的情况下，定位精度会随着小车运行时间增长而有所提高。经过上述试验，如图13 和图14 所示，小车在稳定行驶3 m后即可获得成功率较高的定位结果。算法运行一次所用时间稳定在40 ms 左右，并且受计算机系统硬件影响。

5 结论

本文对实验室内的智能车辆传感器系统进行了参数校正，理论与实践相结合，对于无地图情况下的扩展卡尔曼滤波的航位推测定位技术、地图构建以及有地图情况下的蒙特卡罗定位进行了理论分析与试验验证的系统研究。试验结果表明，航迹推测定位不适用于远距离定位，存在较为明显的累积误差现象，基于地图的定位会对累积误差进行一定的校正，在该情况下位置定位成功率可达70%左右，角度估计成功率在直线轨迹情况下高达90%，曲线轨迹达到74%，表明了地图的重要性。仍存在一定的改善空间，后续研究可以考虑使用Kinect 深度摄像机与激光雷达相结合，继续提高定位精度。