无线光中继通信在弱湍流时的性能估计方法

陈 晓，胡晓英

(上海申核能源工程技术有限公司，上海 200233)

0 引 言

自由空间光通信(Free-Space Optical Communications, FSO)运用激光视距链路可获得每秒几千兆的速率。天气晴朗时，FSO系统的性能主要受制于湍流导致的信号衰落[1-2]。对于短距FSO信道，通常可以用对数正态分布描述其功率。对于温度变化剧烈的环境，例如核电站内部，光通信信道也服从对数正态模型。当链路距离过长或存在障碍物时，可引入中继节点来对抗湍流衰落[3]。对于强度调制/直接检测(Intensity-modulation direct-detection, IM/DD)系统可使用放大-转发(Amplify-and-Forward，AF)协议。

文献[4] 提出了一种数值方法来估计AF系统的性能，但此类方法引入了物理意义不明的间接变量，无法直接揭示信道参数对整体系统性能的影响；文献[5] 研究了FSO多跳中继和平行中继的性能近似表达，但无法得到闭式的AF中断概率表达式。对此，不少文献采用了针对对数正态变量求和的近似[5-6]，其中，Wilkinson和Fenton近似是目前应用最广泛的两类近似方法[7-8]。这两类方法原理相通且运算复杂度相近，但其在不同条件下的选取准则并没有文献进行系统研究。

本文从原点矩的积分表达式上对比了Wilkinson和Fenton近似的特点，讨论了在不同信噪比条件下的近似方法。仿真结果表明，在低信噪比情况下，Wilkinson近似的误差小于Fenton近似；而在高信噪比情况下，Fenton近似的误差则低于Wilkinson近似。

1 光通信中的对数正态信道模型

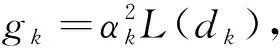
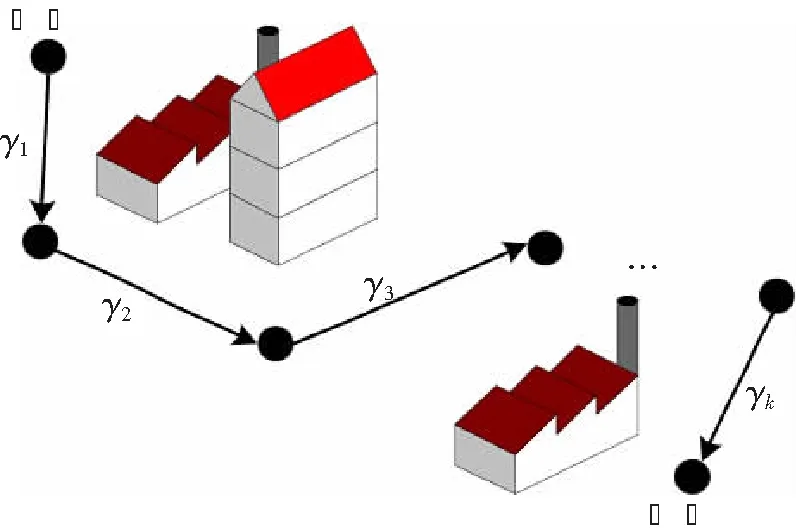
图1 FSO多跳中继系统

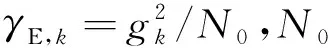
2 Wilkinson和Fenton近似

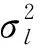
2.1 Wilkinson近似

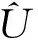
2.2 Fenton近似

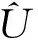
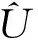
通过求解式(3)可得

2.3 Wilkinson和Fenton近似的积分表达式对比

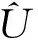
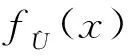
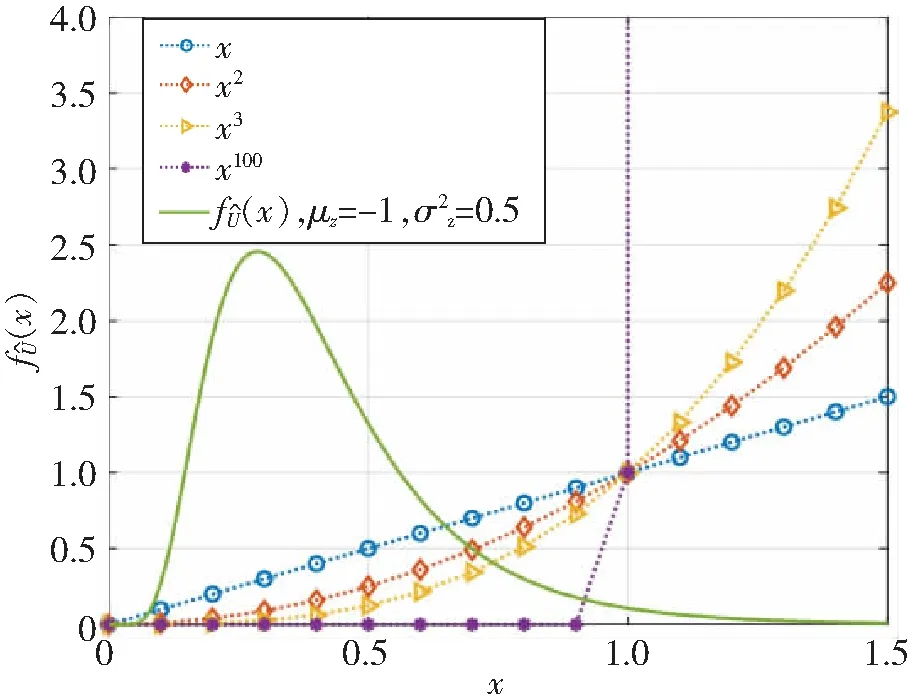
图2 加权函数xr和概率密度函数

式中：n为求和项；Δx→0,N→。式(6)经化简可得

上述的讨论说明，由于匹配了低阶矩，Wilkinson近似对于对数正态变量的和的概率密度函数具有较好的整体近似；而Fenton近似匹配了高阶矩，因此更侧重概率密度函数在x≫1处的近似。该结论将为这两类近似在性能分析中的应用提供准则。

3 Wilkinson和Fenton近似在多跳中继系统中的应用

3.1 近似信宿处的信噪比

根据文献[4] ，K跳AF网络在信宿处的精确信噪比可表示为

式中，γk为第k条链路的瞬时随机信噪比。通过展开，可将式(8)表示为

式中：γE,D为最终节点处经过光-电转换后的电信号信噪比；γE,k为第k跳接收机处的电信号信噪比；o为高阶无穷小项。假设γk→,∀k=1,…,K。根据对数正态变量的性质可知，如果γE,k服从对数正态分布，则也服从对数正态分布，只是对应的μE,k参数需要取相反数。因此如果忽略式(9)中的高阶小量，则可以用Wilkinson或Fenton近似来近似

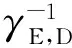
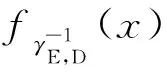
3.2 误码率和中断概率近似公式

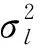
对于FSO多跳AF网络来说，精确的误符号率可通过如下公式计算[14]：

式中：a和b均为固定常数，取决于采用的调制方式；Q(x)为高斯积分函数，在Matlab和Mathematica等软件工具中均为内置函数。例如，当采用二进制相移键控(Binary Phase Shift Keying，BPSK)时，a=1，b=2，式(11)的积分不可化简，且fγE,D(r)的表达式包含K重无法化简的积分。因此，即便利用数值积分方法，式(11)依然是低效且开销巨大的。

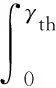
4 仿真结果

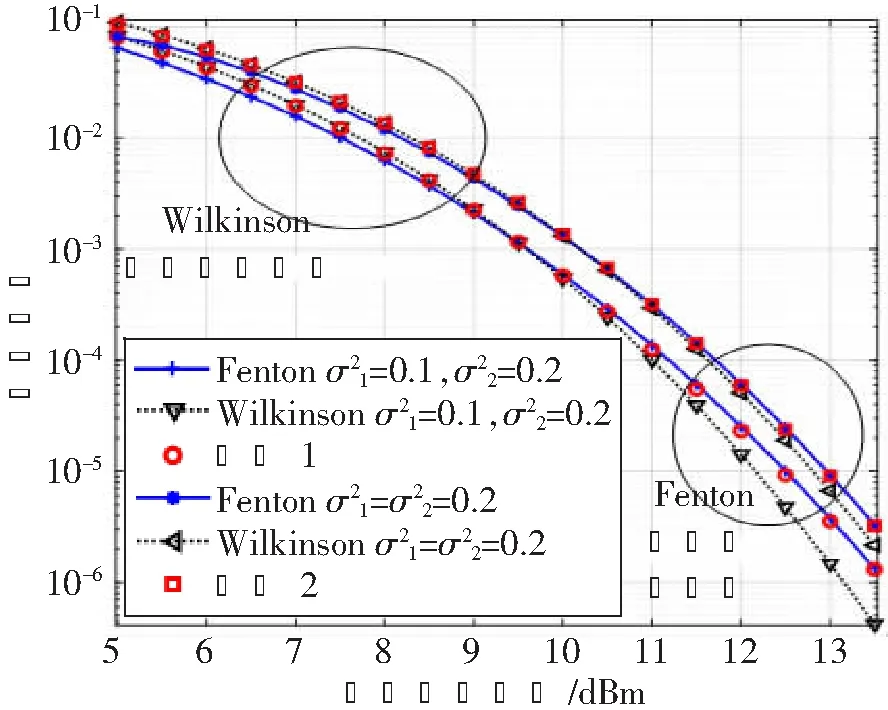
图3 通过Wilkinson和Fenton近似得到的AF多跳系统误符号率

图3和图4共同指出，尽管Wilkinson和Fenton近似都是通过匹配原点矩来对对数正态变量的求和作近似，但由于所取得原点矩阶数不同，因此其适用范围不同。对于FSO AF中继系统来说，在估计中低信噪比情况下的性能时应采用Wilkinson近似；而在估计高信噪比情况下的性能时应采用Fenton近似。

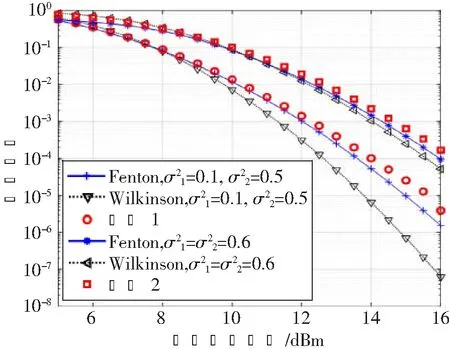
图4 通过Wilkinson和Fenton近似得到的AF多跳系统中断概率

5 结束语

本文对比了Wilkinson和Fenton算法用于近似对数正态和时的引入误差。通过分析不同阶的原点矩匹配公式，得出了Wilkinson方法能够更好地近似概率密度函数的整体形状，而Fenton方法能够更好地近似概率密度函数的右端，即大值部分。在此基础上，得出了AF中继通信系统的近似误符号率和近似中断概率的公式，并指出高信噪比情况下应当采用Fenton近似，而中低信噪比情况下应当采用Wilkinson近似。本文方法回避了复杂的多重积分估计和蒙特卡洛仿真，为无线光中继系统的设计提供了理论工具。