变电站内5G终端通信信道建模与分析
李 欢,许 越,孟凡博,任 帅,李海军,庞晓静
(1.国网辽宁省电力有限公司电力科学研究院,沈阳 110000; 2.中国联合网络通信有限公司智网创新中心,北京 100000;3.国网辽宁省电力有限公司,沈阳 110000; 4. 北京电信规划设计院有限公司,北京 100000)
0 引 言
对变电站中电力设备的巡检至关重要[1-2],许多巡检技术被引进,如高清视频监控[3]、无线射频识别(Radio Frequency Identification Devices,RFID)技术[4]、无人机巡检[5]和巡检机器人[6]等。一台智能巡检机器人可搭载众多设备,不到1小时即可完成所有巡检工作。
光纤是最靠谱的通信方式[7],但移动的机器人无法使用光纤通信。目前巡检机器人一般使用无线局域网(Wireless Fidelity,WiFi),可完成普通巡检任务[8],但WiFi不能满足复杂巡检任务的要求[9]。第五代移动通信(5th-Generation,5G)技术的高速率低时延能充分发挥机器人的能力,出色完成巡检任务[10]。
信道特性影响通信系统的性能,故需要分析5G机器人的通信信道特性并建立准确的信道模型。主流信道建模方法分为3种:射线追踪法[11]、统计法[12]和随机几何法[13]。射线追踪法基于实际传播环境,用麦克斯韦公式推导信号增益表达式;统计法是根据实测数据,运用最小二乘法拟合出信号增益表达式;本文采用随机几何法,根据几何模型推导增益表达式,可分为二维(Two-Dimension,2D)模型[14-15]和三维(Three-Dimension,3D)模型[16-17]建模法。
本文选取偏僻的变电站,可忽略外部散射体对信道的影响,其中5G基站位于巡检区域的中心位置。基站和机器人不在一个水平面,故需要建立3D模型。为提高通信质量,将多输入多输出(Multiple-Input Multiple-Output,MIMO)技术应用于机器人。针对不同的场景环境,改变莱斯因子,分析变电站场景下巡检机器人的5G通信信道的自相关和互相关特性。
1 巡检机器人5G通信信道模型
图1所示为本文所述的变电站场景下5G巡检机器人的通信信道模型图。建立相关的3D坐标系,以地面为x和y轴所在的平面。由于变电站位置偏僻,周围没有什么高大树木和建筑物,散射主要来自变电站内的物体。变电站内有一建筑物的墙(图中阴影部分),长为L,高为4米。墙上有无数个散射体S,坐标为(x,W,z)。5G巡检机器人待巡检的区域是宽为W的矩形区域(图中仅仅画出长为L的部分)。5G巡检机器人M的坐标为(D,0,0),且运动方向为x轴的正方向,速度为v。5G基站在高为H的杆塔上,坐标为(L/2,W/2,H),5G巡检机器人M与墙的水平垂直距离为W。5G巡检机器人上配备有均匀线性天线阵列,有K个天线单元,阵列与x轴的夹角为θ,天线单元的间距分别为δ。第k(k=1,…,K)个发射天线单元Ak到基站的直线距离为dBk。基站到散射体S的直线距离为dBS,散射体S再到第k个天线单元的直线距离为dSk。5G巡检机器人M与5G基站B的通信路径分为两种:一是直射径(Line of Sight,LOS);二是经过墙上散射体的散射路径。5G巡检机器人M到5G基站的LOS路径的方位角为αB,仰角为βB。散射体S到5G巡检机器人M的散射路径的方位角为αS,仰角为βS。

图1 机器人通信信道模型
式中:C为信道的莱斯因子,为LOS与散射路径的功率之比;e为常量;λ为5G频段下信号的波长;j为虚数单位;fLOS为因5G巡检机器人的移动导致的直射路径上的多普勒频移。
式中:n为散射体的序号;N趋于无穷,表示散射体数量无穷大;φ为随机相量,一般认为服从0~2π的均匀分布;fS为因5G巡检机器人的移动导致的散射路径上的多普勒频移。
根据空间几何理论,dBk、dBS以及dSk的大小与LOS的方位角αB和仰角βB以及散射径的方位角αS和仰角βS相关。而这些方位角和仰角又与终端M的坐标、5G基站坐标以及散射体的坐标相关,可以根据空间几何方法推导出相关的表达式,因篇幅问题在此省略,具体的计算方法可参考文献[13]和[16]。
2 空间-时间相关函数
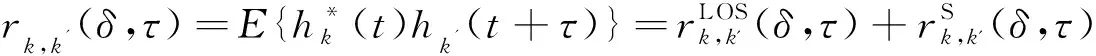
式中,p(x)和p(z)分别为散射体在x和z坐标上的概率密度分布函数。

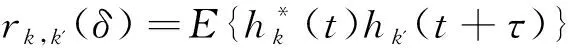
3 相关函数数值仿真与分析
根据第2节推导的ST-CF模型,对信道特性进行理论分析,采用Matlab软件进行数值仿真。
终端M到基站B的通信路径包含LOS路径和散射路径,散射体主要来自墙,墙上散射体的坐标为(x,W,z),x与z的取值决定了散射路径的方位角和仰角。因为建筑物的墙表面平整,没有凸出部分,所以x与z的概率密度分布可取均匀分布。
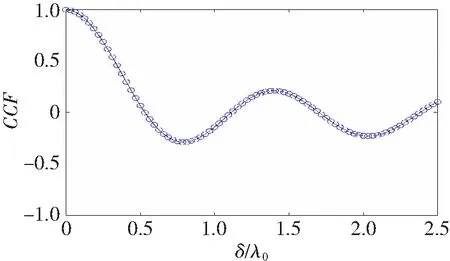
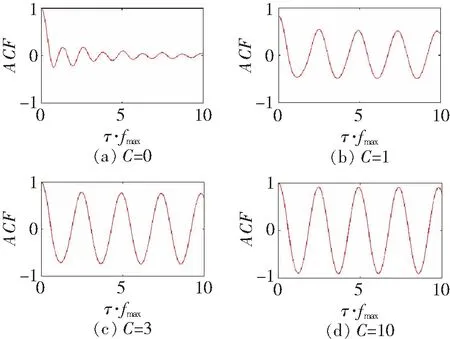
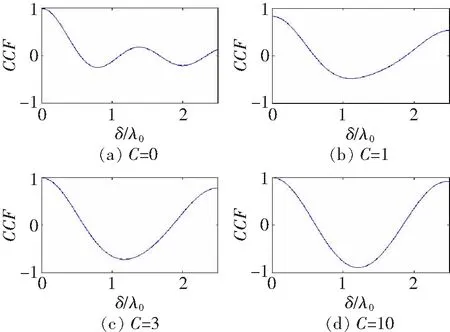
x的概率密度分布函数为p(x)=1/L,0 图2所示为5G巡检机器人与5G基站通信信道的ACF图。信道的自相关特性具有震荡性,随着标准时间间隔的增大,ACF从1逐渐震荡到0。4个标准时间间隔后,ACF在0附近小幅震荡。因为本例的莱斯因子较小(对应着LOS被严重遮挡的情况),C只取了0.05,所以通信信道的自相关特性会随着标准时间间隔的增大而趋于0。 图2 信道自相关特性 图3所示为5G巡检机器人与5G基站的通信信道的CCF图。信道也具有一定的震荡性,与信道的自相关特性相似。随着天线单元间距的增大,信道的空间互相关特性也从1逐渐趋于0,并在0附近小幅震荡。同样,因为莱斯因子取值较小,所以互相关特性最终才会在0附近震荡。 图3 信道互相关特性 为研究莱斯因子C的大小对信道的影响(即信道遮挡的严重性对信道的影响),选取C分别为0、1、3和10这4种情况,其他参数不变。根据第2节推导的信道模型,作出相应的仿真图,如图4和5所示。观察分析C=0、1、3和10的4张图,由图4可知,C越大,ACF曲线震荡越明显,振幅越大;只要C不为0,ACF曲线最终都不会趋于0,而是基于一定的振幅而不断振荡。由图5可知,CCF曲线的震荡与ACF相似,只要C不为0,CCF曲线最终就不会趋于0;C越大,稳定后振荡的振幅越大。 图4 不同莱斯因子下的信道ACF 图5 不同莱斯因子下的信道CCF 综合以上分析可知,C对信道的相关性影响巨大,为提高信道通信的质量,应尽量保证5G基站与5G巡检机器人的通信存在LOS。 针对变电站位置偏僻和站外树木建筑物稀少的特点,结合变电站内巡检区域和机房的特点,本文建立了5G巡检机器人通信的3D信道模型。根据几何分析法,推导出了信道的ACF和CCF公式,并采用Matlab软件工具作出相应的仿真,分析了标准时间间隔对ACF的影响,以及天线单元的间距对CCF的影响。由于变电站内巡检区域的电力设备会对5G基站和巡检机器人之间的通信造成遮挡,必须考虑莱斯因子对信道的影响。选取不同的莱斯因子作仿真分析,对比不同莱斯因子下信道的ACF和CCF可知,莱斯因子越大,信道的相关性越大,无线通信质量越好。本文针对变电站场景内5G巡检机器人的通信信道建立3D模型,分析信道的相关特性,扩宽了5G+机器人在变电站内的应用研究。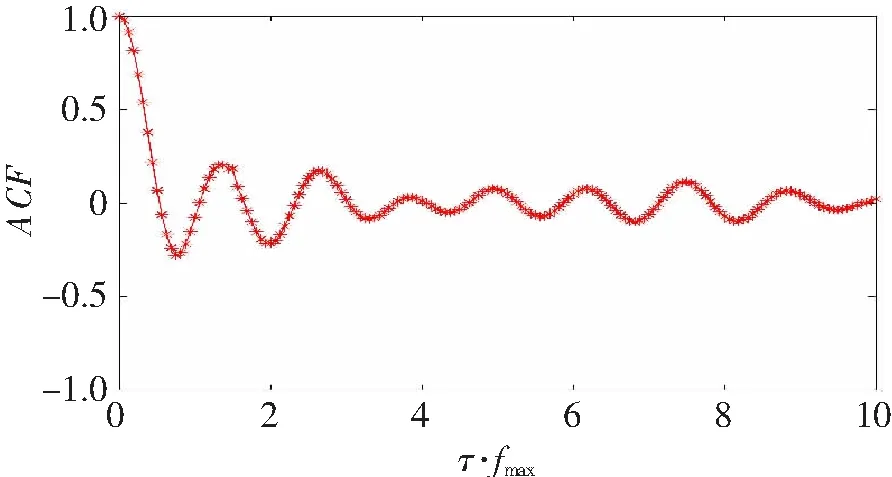
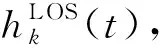
4 结束语

