基于增量反推控制的机械弹性储能用永磁同步电机控制方法

余洋， 冯路婧， 米增强， 韩帅

(1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003； 2.华北电力大学 河北省分布式储能与微网重点实验室，河北 保定 071003； 3.广西电网有限责任公司电力科学研究院，南宁 530023)

0 引 言

能源消耗和环境污染的双重压力，促使我国提出了构建以新能源为主体的新型电力系统发展目标。新能源出力呈现随机性、间歇性的特点[1-3]，储能技术是应对规模化新能源入网有效途径之一[4-6]。相较于其它储能技术，以涡簧为储能媒介的机械弹性储能因其安全性强、转换效率高、对环境友好、无静态损耗等优势，成为了当下研究热点[7-8]。

永磁同步电机(permanent magnet synchronous motor, PMSM)结构简单、转矩惯量比大、运行效率高[9-10]，机械弹性储能利用其作为储能电机，通过变流器控制PMSM拧紧涡簧，实现电能向机械能的转换与存储[11]。在储能过程中，涡簧不断向芯轴收缩形变，使其扭矩和转动惯量同时变化。研究表明[12-13]，PMSM传统矢量控制难以适应机械弹性储能系统多变量、强耦合和负载特性时变等非线性特点。为此，当前研究引入了反推控制(backstepping control, BC)这种非线性控制方法以期获得更好的控制性能[14-16]。但反推控制作为基于模型的控制方法，对模型参数的不确定性较为敏感，同时受环境温度、振动等因素影响，现场运行中很难获得准确的PMSM模型信息，由此弱化了反推控制的控制性能[17-18]。

增量反推控制策略(incremental backstepping control, IBC)是在反推控制的基础上，利用附加的测量值来取代部分所需的模型信息，以降低反推控制对于系统模型的依赖性，提高控制的准确性和鲁棒性。不过增量反推控制并非完全取消显式模型中的所有参数，它是一种处于模型和传感器测量之间的控制算法。当前，增量反推控制已被成功引入飞行器等控制领域，如文献[19]利用增量反馈控制，处理飞行控制系统中存在的模型和参数不确定性问题；文献[20]设计了一种基于非线性扰动观测器的增量反推控制器，用于提高飞行器跟踪位置指令的准确性，但还未见将增量反推控制应用于PMSM控制的报道。另外，当前对于增量反推控制的研究还较为浅显，大部分研究只是在相关领域中利用增量反推控制理论构建控制框架，未见增量反推控制用于PMSM的报道，更未见有针对性地研究增量反推控制参数选择的成果。

针对机械弹性储能系统涡簧负载固有时变特性和模型参数非线性特征，基于增量反推控制理论，本文推导设计了PMSM速度增量反推控制器和电流增量反推控制器，并进行了鲁棒性分析和控制参数的确定。仿真结果表明，与常规反推控制相比，本文提出的增量反推控制具有较强的参数鲁棒性，对于参考信号的跟踪速度更快、动态性能更好，能够实现机械弹性储能系统的平稳储能。

1 机械弹性储能系统数学模型

图1给出了以PMSM为执行机构的机械弹性储能系统结构示意图，该系统主要包括四部分：涡簧箱、PMSM、AC-DC-AC功率模块和控制器。

图1 机械弹性储能系统结构示意图Fig.1 Structural diagram of mechanical elastic energy storage system

机械弹性储能系统采用表贴式PMSM，其在dq0同步旋转坐标系下的数学模型[21-22]可表示为：

(1)

式中：ud、uq为d、q轴的定子电压；id、iq为d、q轴的定子电流；LN为定子电感标称值；RN为定子电阻标称值；BN为粘滞摩擦因数标称值；φfN为永磁磁通标称值；J为等效转动惯量；TL为负载转矩；np为转子极对数；ωr为转子机械角速度。

根据材料力学知识[12]，储能时涡簧作为负载，假设涡簧材料的弹性模量、厚度、宽度和长度可分别表示为E、h、b和L，则负载转矩TL和等效转动惯量J分别描述为：

(2)

(3)

式中：TL0为涡簧的初始扭矩；δ、ωs为涡簧芯轴转过角度和转速；c1为涡簧转矩系数，对于矩形截面的涡簧，c1=Ebh3/12L；ns为涡簧总储能圈数；Je为涡簧完全释放时的转动惯量。

2 常规反推控制方法

实际中，受环境和运行条件影响，定子电感、定子电阻等可能偏离各自的标称值而呈现不确定性，模型不确定性将影响控制器的目标性能和稳定性，此部分将在第三节鲁棒性中详细分析。因此设计控制策略过程中，采用模型的实际值代替标称值，修改后的PMSM数学模型可表示为：

(4)

式中：L、R、B和φf分别表示定子电感、定子电阻、粘滞摩擦因数和永磁磁通的实际值。

定义转速跟踪误差为

eω=ωref-ωr。

(5)

式中ωref为转子参考机械角速度。

定义电流跟踪误差为：

eq=iqref-iq；

(6)

ed=idref-id。

(7)

式中：iqref为q轴参考电流；idref为d轴参考电流。

定义第一个李雅普诺夫函数为

(8)

对式(8)求导可得

(9)

(10)

式中kω为正的控制参数。

根据式(10)得到控制量

(11)

即q轴参考电流为

(12)

同时假设d轴参考电流为

idref=0。

(13)

分别对电流跟踪误差eq、ed求导可得：

(14)

(15)

定义第二个李雅普诺夫函数为

(16)

对式(16)求导可得

(17)

(18)

(19)

可得：

(20)

ud=Rid-Lnpωriq+Lkded。

(21)

据此，常规反推控制器的最终形式为：

(22)

3 增量反推控制及参数鲁棒性分析

3.1 增量反推控制器设计

根据增量控制原理，q轴电流的导数可改写为

ω0Δid+Δωrid0+ΔωrΔid)-

(23)

(24)

式中ΔT为采样时间间隔。

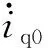
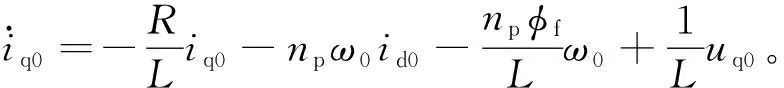
控制量的增量Δuq直接影响系统，而状态量的增量Δiq、Δid和Δωr间接影响系统性能，因此状态量的增量一般比控制量的增量慢，故Δiq、Δid和Δωr比Δuq小得多。为此，与控制量的增量相比，状态量的影响可以忽略不计。

据此，q轴电流的导数可近似表示为

(26)

同理，d轴电流的导数可改写为

(27)

其中

(28)

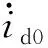
(29)

d轴电流的导数可近似表示为

(30)

分别对电流跟踪误差eq、ed求导可得：

(31)

(32)

定义李雅普诺夫函数为

(33)

对式(33)求导可得

(34)

(35)

(36)

可得：

(37)

(38)

因此，增量反推控制器的表达式为：

uq=Δuq+uq0；

(39)

ud=Δud+ud0。

(40)

3.2 参数鲁棒性分析

将常规反推控制器式(20)和式(21)改写为：

(41)

ud=L[kded+f2(iq,id,ωr)]。

(42)

其中：

(43)

(44)

由此，可得到常规反推控制策略的控制框图，如图2所示。与此同时，由式(39)、式(40)可绘制增量反推控制策略的控制框图，如图3所示。

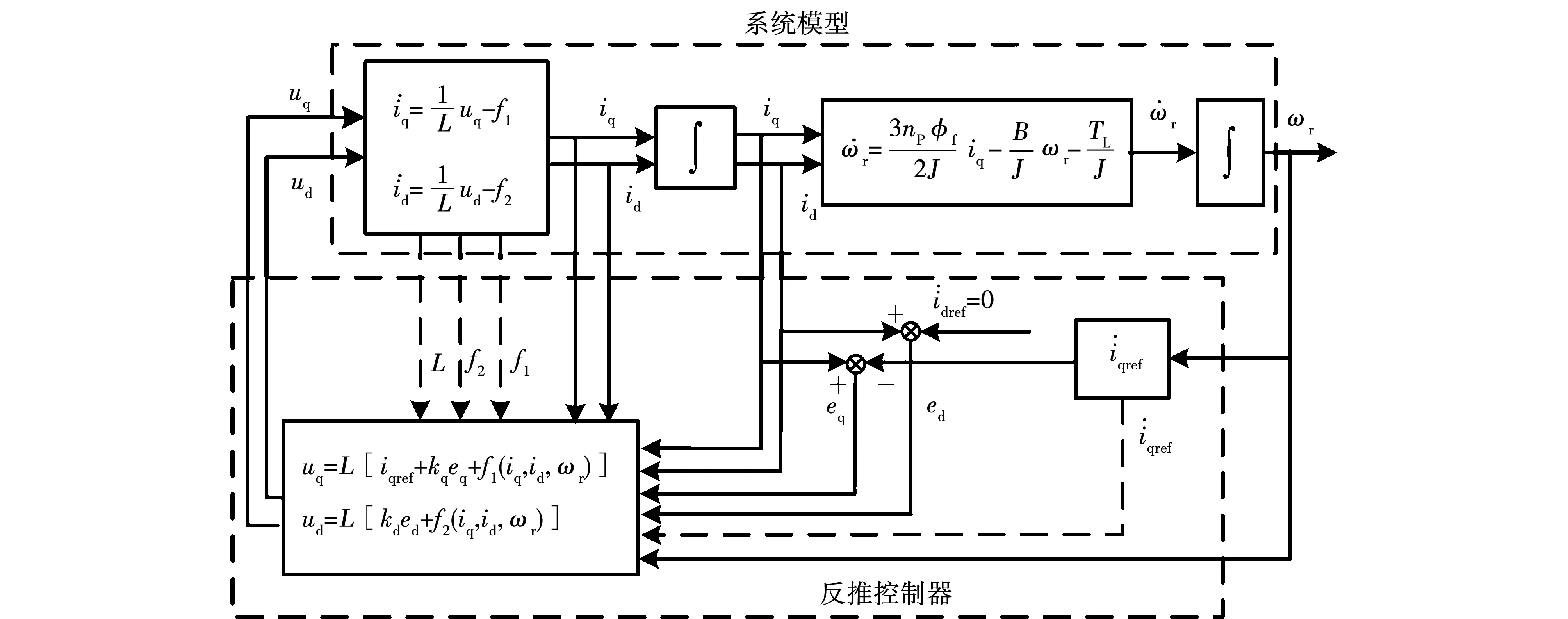
图2 常规反推控制策略控制框图Fig.2 Control block diagram of conventional backstepping control

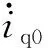
图3 增量反推控制策略控制框图Fig.3 Control block diagram of incremental backstepping control

因此，只需分析定子电感L的不确定性对增量反推控制器鲁棒性产生的影响。

为此，定义定子电感L的不确定性为

(45)

式中ΔL为定子电感实际值L与定子电感标称值LN的差值。

将定子电感L的不确定性γ代入式(37)得到

(46)

(47)

由式(45)得到q轴电流控制框图，如图4所示。

定子电感L的不确定性γ存在两种情况：

1)γ=1。

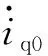
(48)

图4 q轴电流控制框图Fig.4 Control block diagram of q-axis current

2)γ≠1。

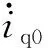
(49)

由式(48)和式(49)可知，两种情况下传递函数相等，因此定子电感L的不确定性γ对电流控制环节影响很小，即增量反推控制对定子电感参数变化具有鲁棒性。

因此，增量反推控制器的最终形式为：

(50)

4 增量反推控制器控制参数选择分析

4.1 电流环控制参数

将式(39)代入式(4)，可得q轴电流的导数为

(51)

由此，电流环节传递函数Gi(s)可写为

(52)

由式(52)可得到电流环节中控制参数的稳定性条件为

kq>0。

(53)

4.2 速度环控制参数

双闭环控制系统中电流环可视为转速环的一个环节，将式(52)代入式(4)，可得到转速ωr的导数为

(54)

据此，可得到速度环闭环传递函数为

(55)

二阶系统的调节时间可写为

(56)

式中ωn、ζ分别表示速度环的固有频率和阻尼比。

由式(55)结合式(56)，速度环调节时间可具体写为

(57)

若要求系统调节时间ts小于tl，可得到q轴电流控制器参数需满足如下条件：

(58)

根据式(55)，进一步写出系统超调量为

(59)

若要求系统超调量σ%≤c，可得到速度控制器参数需满足条件：

(60)

5 仿真分析

为验证本文提出的增量反推控制器的有效性，在MATLAB平台中进行仿真分析。通过电流和速度跟踪效果观测控制器性能。PMSM和涡簧材料额定参数分别见表1和表2。恒扭矩负载转动惯量J为0.03 kg·m2，负载扭矩TL为10 N·m。

表1 永磁同步电机参数

表2 涡簧材料参数

取系统调节时间ts≤0.07 s，系统超调量σ%≤40%，根据式(55)、式(57)以及增量反推控制原理确定增量反推控制器参数范围为：00。再经过多次仿真实验，确定出一组效果较好的控制器参数为kω=150、kq=3 000和kd=350。

为了更好地测试增量反推控制的性能，将本文算法与常规反推控制和矢量控制进行比较，分析对比不同控制算法下的跟踪效果。取常规反推控制器参数与增量反推控制相同，即kω=150、kq=3 000和kd=350。

仿真实验共分为4组，第1组为PMSM额定参数条件下驱动恒转矩负载仿真实验；第2组PMSM额定参数条件下驱动涡簧负载仿真实验；第3组噪声干扰下PMSM驱动涡簧负载仿真实验；第4组为PMSM参数偏离额定值时驱动涡簧负载仿真实验。

仿真时间设置为10 s，初始时刻参考转速ωref=2 rad/s，2 s时刻参考转速突变为5 rad/s，6 s时刻恢复至2 rad/s，直到仿真实验结束。4组仿真下的实验结果分别如图5～图8所示。

对比图5(a)和图6(a)可见，额定参数条件下，对于不同的ωref，常规反推控制和本文方法均能实现转速追踪，不过常规反推控制算法调节速度相对较慢；而本文算法在驱动恒转矩负载和涡簧负载时，均可准确快速地跟随转速指令的改变，且动态响应性能更优。

图5 PMSM额定参数条件下恒转矩负载控制效果比较Fig. 5 Control effect comparison of constant torque load under PMSM rated parameters

图6 PMSM额定参数条件下涡簧负载控制效果对比Fig.6 Control effect comparison of spiral spring load under PMSM rated parameters

对比图5(b)和图6(b)表明，额定参数情况下，相比常规反推控制算法，本文方法在2、6 s参考转速剧烈变化时，iq的波动更小，且重新回到稳定状态的时间更短；由图5(b)可见，iq与涡簧扭矩呈正比关系，当参考转速不变时，iq的增大速度也不变，当参考转速增大后，iq的增大速度也随之增大，且iq随着参考转速突变而发生改变。

从图5(c)和图6(c)可以看出，额定参数情况下，不同的参考转速下，常规反推控制和本文算法均将d轴电流控制至参考值附近。但相较本文算法，常规反推控制算法下id的波动较大。

系统实际运行过程中，若电流采样值中含有测量噪声，图7(a)、图7(b)和图7(c)给出了噪声干扰下PMSM驱动涡簧负载的转子转速ωr、q轴电流iq和d轴电流id的变化情况。由图7(a)可见，相较常规反推控制，本文算法受噪声条件影响影响较小，转速波动在可接受范围内。由图7(b)和图7(c)可见，常规反推控制和本文算法均能均将电流控制至参考值附近，但常规反推控制电流的毛刺较多，不利于系统平稳运行。

图7 噪声干扰下PMSM驱动涡簧负载控制效果对比Fig.7 Control effect comparison of spiral spring load driven by PMSM under noise interference

图8 PMSM参数变化时驱动涡簧负载跟踪效果对比Fig.8 Tracking effect comparison of spiral spring load driven by PMSM under changed parameters

图8给出了增量反推控制、反推控制和矢量控制下PMSM参数变化对转速跟踪性能的影响情况，其中定子电阻不确定性γR=RN/R，定子电感不确定性γ、定子电阻不确定γR的取值均设定为1、1.5和2。对比图8(a)、图8(b)和图8(c)可见，转速参考值变化时，矢量控制下的转速波动较大且波动时间较长；相较于常规反推控制和矢量控制，定子电阻R的不确定性对增量反推控制系统的转速跟踪效果基本没有影响；从图8(d)、图8(e)和图8(c)可见，定子电感L的不确定对增量反推控制系统的转速跟踪效果有一定影响，但相较于常规反推控制和矢量控制影响很小，系统在波动后迅速恢复到稳定状态。因此，在本文控制方法的作用下，虽然模型参数发生了扰动变化，但转速跟踪误差较快速且平稳地保持于零值，证明了本文控制方法确实具有较强鲁棒性。

综上，仿真结果表明，相对于常规反推控制和矢量控制，增量反推控制算法的控制效果更优，具有更强的鲁棒性，可实现机械弹性储能系统快速平稳储能。

6 结 论

机械弹性储能系统通过控制永磁同步电机拧紧涡簧实现储能，该过程表现出非线性的特点。为达到良好的控制效果，本文在常规反推控制基础上，设计了用于机械弹性储能系统储能控制的永磁同步电机增量反推控制方法，通过研究得到以下结论：

1)相比于常规反推控制，本文方法具有较强鲁棒性，对系统参数变化不敏感，更适应机械弹性储能系统；

2)与常规反推控制相比，本文方法下永磁同步电机可准确快速地跟踪指令的改变，在参考转速剧烈变化时，转速及电流的稳定性及动态性能更好；

3)依据系统控制性能对增量反推控制器参数的分析和整定，可以在满足系统稳定性基础上进一步提高系统动态性能。