基于粒子群算法估计实际工况下锂电池SOH

南金瑞， 孙路

(1. 北京理工大学 电动车辆协同中心，北京 100081； 2. 北京理工大学 机械与车辆学院，北京 100081)

不断持续的能源危机和环境保护问题促使着电动汽车技术的更新迭代[1-2]. 锂离子电池以其高能量密度、低自放电率和循环寿命长等优点作为动力电池为电动汽车提供动力. 电池健康度(state of health, SOH)这一指标来表示锂电池的老化程度，通过对SOH的实时估计和预测，可以保障电池包整体的充、放电性能[3].

目前，对于锂电池SOH估计主要有两方面：基于模型的方法从锂电池自身的衰退机理出发对电池进行建模[4]，利用等效电路模型能够在一定精度范围内对电池SOH进行估计，经验衰退模型基于大量数据，用数据拟合的方式构建锂离子电池在使用过程中容量衰退随循环周期的函数模型，此方法对样本数据的波动敏感，预测结果容易发散[5]；基于数据驱动模型包括人工神经网络、时间序列模型、支持向量机等. Rezvani等[6]建立阻抗与容量关系模型，在数据量足够时效果良好,但是在数据量较小的时候误差较大； Luo等[7]应用非线性优化方法确定模型参数以构建SOH估计模型，虽然实时性较好,但是误差较大. 董汉成等[8]应用粒子滤波算法对电池SOH进行估计，虽然精度较高，但是模型收敛速度慢.

1 实际工况锂电池SOH估计模型初值计算

1.1 特征值提取

恒流恒压(CCCV)充电过程的电流、电压曲线可以提取多种反映电池老化状态的特征值，比如恒流段时间、恒压段时间等. 在这里选择NASA电池老化试验中的3块电池(RW3、RW4、RW5)作为训练集进行分析，其余的参与老化实验的9块电池(RW1、RW2、RW6、RW7、RW8、RW9、RW10、RW11、RW12)作为验证集，表1所示为电池的参数.

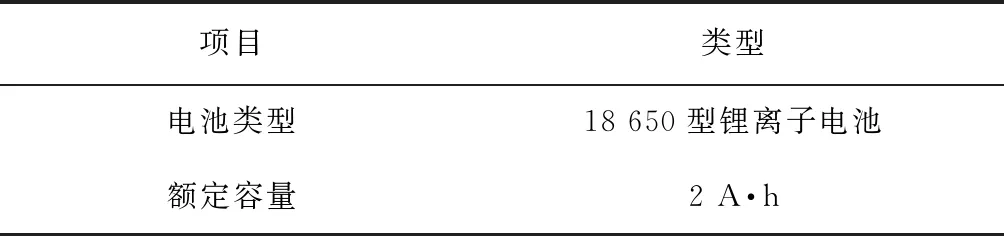
表1 实验电池参数

皮尔逊系数能反映两个对象之间的线性相关程度，如式(1)所示.

(1)

式中:ρq,xi为归一化后的特征值xi与归一化后的电池容量q之间的相关系数，将特征值xi带入上式之后，选择相关系数ρq,xi>0.95的特征作为本文的输入数据. 最终选择结果为：恒流段电压从V0+ΔV/3升高到V0+2ΔV/3所用的时间t1,电压从V0+2ΔV/3升高到Vc所用的时间t2以及恒流段电压从2ΔV/3开始5min内升高的电压值V，其中，V0为初始电压，ΔV为恒流段电压增量，如图1所示为提取的特征值的几何意义.

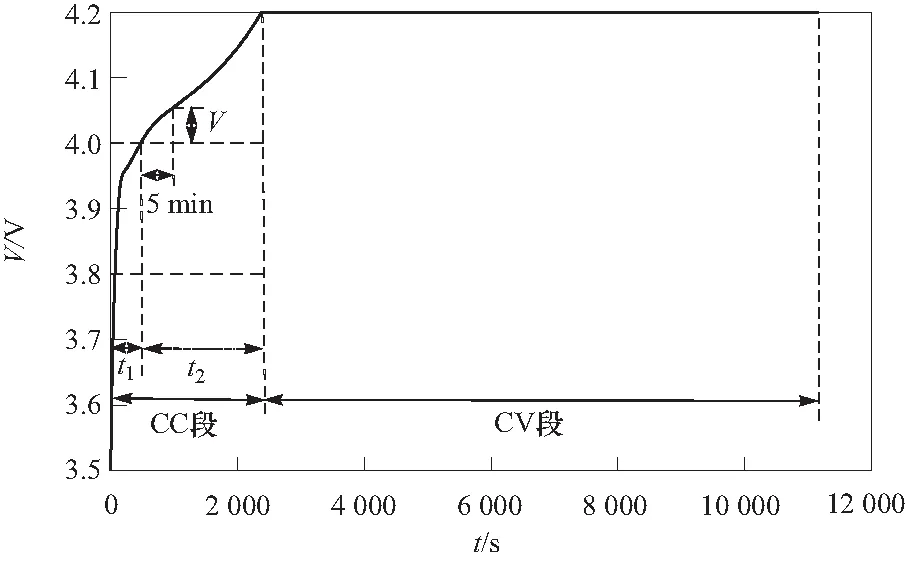
图1 提取的三个特征值t1、t2和VFig.1 Characteristic values t1、t2 and V

1.2 标定充电工况锂电池SOH线性估计模型

在粒子群算法中选取合适的初值，对于模型训练的准确度以及模型收敛的速度有着重要的作用，为此，首先分析标定工况下电池SOH预测模型.

在实验中，三块电池的运行工况包括实际循环工况和标定工况. 循环工况内的放电电流取值从一个放电电流序列中随机选取，该序列电流值均匀分布，且被选用作为放电电流的概率相等. 试验过程为标定工况实验与40个循环工况交替进行，直到电池达到失效条件，其中标定工况流程为CCCV充电、CC放电、CCCV充电、CC放电、脉冲放电.

训练样本中RW3初始容量为2.007A·h，最终容量为1.559A·h，标定工况样本数为9；RW4初始容量为1.981A·h，最终容量为1.593A·h，标定工况样本数为8；RW5初始容量为1.968A·h，最终容量为1.568A·h，标定工况样本数为9. 对所选数据集中标定工况下的充电数据进行特征提取，并利用安时积分法计算标定工况下电池的可用容量QC,i，计算式为

(2)

如图2所示，所选取的三个特征和容量有较强的线性相关性.

由于三个特征以及可用容量量纲不完全一致，需要对提取的每个特征以及可用容量进行归一化处理，构建经过归一化处理之后的特征矩阵

以及和可用容量向量q=[q1q2…qn]，归一化方法如式(3)所示：

(3)

式中：aij为归一化后的特征值；xij为提取到的特征初值. 基于所选特征的标定工况下的SOH线性估计模型为

(4)

式中：Qc为电池可用容量的线性模型的输出；Q0为电池的初始容量；ωi为第i个健康因子的权重值；ai为提取的特征值；b为阈值. 以RW3、RW4以及RW5为训练数据，用最小二乘法进行拟合，得到：ω1=0.305，ω2=0.392，ω3=0.311，b=1.587.

将验证集数据重复上述步骤并计算验证集误差，计算方法如式(5)：

(5)

式中：n为同一块电池老化实验中，标定工况的个数. 验证集误差如图3所示，误差均小于1.0%，按照数据驱动的方法论，此误差较小，满足估计需求.

图3 模型验证结果Fig.3 Model verification results

2 实际工况锂电池可用容量估计

在电动汽车实际的使用工况中，实际使用工况更为复杂，因此需要应用合理的方法估计电池样本中实际充电工况的可用容量. 电池容量经验模型为解决上述问题提供了有效方法，以循环次数为输入量、电池最大可用容量为输出量建立数学表达式，如式(6)所示：

Qc,0(b1eb2k+b3eb4k)

(6)

(7)

式中：ΔkE(i,i+1)为第i次与第i+1次标定工况之间的的当量循环次数；ΔQacc(i,i+1)为两次标定工况之间的累计充入电量;Qc,i与Qc,i+1分别为第i次与第i+1次电池当前可用容量. 拟合kE- Qc,i曲线，得到电池容量模型如图4所示，图中R2为决定系数，其越接近1表示效果越好，它的计算方式如式(8)所示.

图4 电池容量经验模型Fig.4 Battery capacity empirical model

(8)

(9)

3 实际工况锂电池SOH估计模型

3.1 粒子群算法流程

粒子群算法也叫做鸟群觅食法[9]，简写为PSO，该算法属于进化算法，以随机的解为起点，通过不断迭代寻找最优目标解. 粒子群算法流程如下：

① 随机初始化一个粒子群(数量为p)，其中第i个粒子在n维空间中的位置可以表示为Xi={xi1,xi2,…xin}，其速度为Vi={vi1,vi2,…vin}；

② 在每次迭代过程中，粒子通过两个极值来更新自己的速度和位置：一个是单个粒子从初始状态到当前迭代次数搜索产生的最优解，称为个体极值Li={li1,li2,…lin}；另一个是种群目前的最优解，称为全局最优解Gi={gi1,gi2,…gin}.

定义适应度函数如式(10)所示.

(10)

式中：R为观测噪声方差;yk为当前时刻观测量;ypred为预测观测量. 粒子群算法通过计算适应度值将所有的粒子向全局最优粒子移动，从而得到全局最优解.

3.2 实际充电工况锂电池SOH估计模型

由于实际充电工况下，充电曲线几何特征发生了较大程度的畸变，但是这些特征仍然能反映电池的老化状态，为此对提取的特征做指数平滑，如式(11)所示.

St=βSt-1+(1-β)θt

(11)

式中:St为当前量经过指数平滑后的值；θt为当前的观测量；β为加权系数，0<β<1. 一般来说，数据波动越大，选取的β也越大，这里β=0.95.

如前文所选的三个特征值，经过指数平滑之后分别为，st1、st2以及Vs，根据所选的三个特征值建立实际工况电池SOH估计模型如式(12)所示.

Qc=W1st1+W2st2+W3Vs+B

(12)

式中：Qc为电池的可用容量估计值，W1、W2、W3为各个特征的权重；B为阈值.

模型的训练数据为经过指数平滑的特征值st1、st2、Vs和经过容量经验模型估计的实际工况下电池容量的估计值组成时间序列集合. 其中，粒子群算法的初始值设置为标定工况下SOH估计模型的权重和阈值.

将编号为RW3、RW4、RW5的电池作为训练集，最终，通过粒子群算法的优化，可得实际工况下锂离子电池的SOH估计模型的权重如表(2)所示.

表2 经粒子群算法优化的SOH估计模型参数

Tab.2 SOH estimation model parameters optimized by particle swarm optimization

参数数值W12.68×10-4W22.04×10-4W3-2.25B1.59

由于标定工况下的电池可用容量是通过安时积分法计算所得的真值，所以在这里定义误差只在标定工况下进行计算，计算方法为

(13)

式中：n为电池标定工况数量；Qc,i为标定工况下安时积分法所得电池可用容量；Qc(i)为模型预测的电池可用容量. 根据式(13)计算验证集SOH的预测值，再计算模型验证集误差如图5所示. 验证集最大的误差为1.06%，证明此模型有很好地收敛程度，准确性优于基于模型的方法，此外由于模型实时性强，有实际意义. 这里提出的模型是针对电池单体提出的，在实际应用中应当结合电池包特性，对模型进行修正，以使模型能够应用于准确估计电池包的SOH.

3.3 实验验证

在上文中搭建了锂电池健康状态SOH的估计模型，为进一步验证模型的实用性以及准确性 ，采用某公司生产的18650型磷酸铁锂电池作为实验对象，随机选择两个单体做寿命试验，验证模型准确性，其中：编号为CS1的电池单体初始容量为1.912A·h，标定工况数为7；编号为CS2的电池单体初始容量为1.935A·h，标定工况数为6. 特征提取情况如图6所示.

图6 验证实验充电特征提取Fig.6 Verify experiment charging feature extraction

将特征值带入式(12)计算估计值，与标定工况下的实际值做对比，编号为CS1与CS2的电池SOH模型预测的准确度分别为94.7%与93.3%，精确度较高. 但是，这里的研究仅围绕NASA电池老化数据以及实验条件下的电池老化试验数据，并未考虑环境因素的影响，后续应该开展多种电池在不同环境条件下(综合考虑温度、机械应力、电池应用环境等因素)的老化试验，对模型进行适应性分析与验证. 此外，这里的实验以及分析均对于电池单体，后续应开展成组的电池包的分析，并结合均衡控制得到成组电池包准确的健康状态.

4 结 论

电动汽车动力电池SOH估计的准确程度直接影响动力电池的使用以及电动汽车的安全性，有着重要的作用. 根据第三节中对NASA数据集的模型训练与验证以及实验对模型的验证，这里采用的基于粒子群算法的锂电池SOH可以很好地估计实际运行工况中电池的健康度，其实验验证准确度达到93%以上，与传统的基于模型的方法相比，此方法准确性以及鲁棒性更高，适应性更强；与其他数据驱动的方法相比，由于此方法以线性模型为基础，其收敛更快，实时性更强. 在工程应用中，实时性对于SOH估计至关重要，凭借高准确性以及快速收敛的特性，实际意义更大.