一种含放大机构隔振器的动力学特性研究

刘国勇， 赵鹏鹏， 刘海平

(北京科技大学 机械工程学院，北京 100083)

刚度和阻尼是机械系统或结构振动控制领域的两个关键因素. 而常见工程材料的刚度(弹性模量)和阻尼呈相反的变化规律，即刚度越大，阻尼越小. 然而，在实际工程应用中则希望结构同时兼具高刚度和高阻尼的力学特征. 以海上钻井平台为例[1]，海浪冲击时，高刚度结构可以承受冲击载荷作用，同时高阻尼结构可以有效耗散振动能量从而降低系统结构的动态响应并延长其使用寿命.

为了解决上述问题，科研人员通过对结构系统引入高刚度高阻尼隔振器实现动态响应的有效抑制. Dong等[2]通过利用两端平头杆的屈曲力学行为实现对结构负刚度和迟滞阻尼特性的放大. Antoniadis等[3-6]通过在线性隔振器中引入负刚度单元提出一种具有超阻尼输出特性的隔振系统. 从理论方面系统研究了在常规隔振系统中引入负刚度单元后，隔振系统高阻尼输出的工作机理和影响因素. 以上多种隔振器均可在保证隔振系统刚度不降低的情况下，实现高阻尼输出. Bian等[7-8]从仿生学角度提出采用X形机构引入非线性阻尼，研究发现谐振振幅被极大衰减. Liu等[9]将多层X形机构与杠杆系统组合构成准零刚度隔振器，采用力控制可以有效调节系统反共振频率和低频范围的传递特性. Jing等[10]创新性的提出采用多层X形机构构建反共振隔振装置. 研究表明，在保证设备正常负载条件下，反共振隔振装置可显著减小系统动态载荷的传递. Dai等[11]以航天器在轨非合作目标抓捕过程中周期或者冲击载荷作用下产生的微振动为控制目标，采用多层X形机构建立机械臂和末端执行机构之间的隔振装置. 研究表明，多层X形机构组成的隔振装置可以有效控制自由悬浮状态卫星平台和被捕获目标之间的动态响应. Feng等[12]通过观察人体四肢运动过程中的力学关系，建立内含X形机构的反共振隔振器模型. 研究表明，此类反共振隔振器具备优良的低频宽频减隔振性能. Cheng等[13]提出采用受拉伸载荷作用的X形机构建立准零刚度隔振装置. 综上，X形机构的几何非线性特征对隔振器的刚度和阻尼均具有改善作用，通过合理选择结构参数可放大隔振系统的刚度和阻尼性能.

文中提出一种含放大机构的隔振器，其核心是利用X形机构实现对隔振系统阻尼和刚度特性放大. 该隔振系统具有结构简单、可靠性高、适用性强、使用灵活，易于制造和实施等优点.

1 含放大机构隔振器动力学建模

含放大机构隔振器的力学模型如图1所示. 图中,m为惯性质量；kv和kh分别为隔振器沿垂直方向和水平方向的弹簧刚度；l为单根刚性杆的长度；四根刚性杆两两铰接，刚性杆与水平轴y的初始夹角为θi；c为阻尼系数；受基础激励Z作用；刚性铰接杆与水平轴的夹角变量为φ；t为时间. 假设，垂向向上为x轴正方向，水平方向向右为y轴正方向.

由图1所示力学模型，得到系统沿x轴方向的运动方程为

(1)

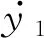
图1 隔振系统力学模型Fig.1 Mechanical model

根据图1所示X形机构的几何关系，得到

(2)

(3)

y1=-y2

(4)

(5)

假设基础所受激励为Z=Z0cosωt，则式(1)表示为

(6)

为了方便计算，需要对式(6)进行化简，定义函数：

f1(x)=2kh(lcosθi-

(7)

(8)

由于函数f1(x)和f2(x)在x=0处连续，将式(7)和式(8)在零平衡位置采用三阶泰勒级数展开，可得

f1(x)=β0+β1x+β2x2

(9)

f2(x)=β3+β4x+β5x2

(10)

为了方便计算，对式(11)引入量纲一的参数，

(11)

式中:ωn为隔振系统固有频率;τ为量纲一时间;γ为隔振器纵横刚度比;Ω为频率比;u为量纲一位移，ξ为阻尼比;z0为量纲一的激励位移幅值.

将式(9)(10)代入式(6)，并进行量纲一化后得到：

(12)

采用谐波平衡法对式(12)进行求解. 假设其稳态解的形式为

u=u0cos(Ωτ+φ)

(13)

式中:u0为位移幅值;φ为初始相位. 求解后可得：

(14)

为了方便表示，定义：

(15)

(16)

(17)

由式(14)就可以解得位移激励条件下隔振统的幅频响应和相频响应

(18)

(19)

式中，Ω上标d代表位移激励，下标则表示幅频响应曲线由两部分组成，两条曲线的交点即为响应幅值的最大值.

2 等效刚度系数和等效阻尼系数

2.1 等效刚度系数分析

与线性隔振系统类比，含放大机构隔振系统的等效弹性恢复力为

(20)

式(18)对x进行求导后即可解得系统的等效刚度系数为

(21)

式中，Kd即为X形机构隔振器的等效刚度系数. 由式(21)可以看出，等效刚度系数是以x为变量的线性函数，因此不再分析x对等效刚度系数的影响，仅对设计参数θi和kh进行分析. 暂定θi范围为[30°,60°]，kh范围为[-20 N/m,20 N/m]，x的值为0.001 m，kv为2 000 N/m. 由式(21)即可给出等效刚度系数随θi、kh的变化规律. 可以得出，当水平刚度小于0时，随着初始倾角增大，等效刚度系数呈非线性规律减小；当水平刚度大于0时，随着初始倾角增大，等效刚度系数呈非线性规律增大；且在刚度系数为-20 N/m、初始倾角为60°时等效刚度系数达到最小，刚度系数为20 N/m、初始倾角为60°时等效刚度系数达到最大. 因此，通过调整水平刚度和初始倾角可对隔振系统的有效隔振频段进行调节，可以使含放大机构隔振器可实现刚度放大.

2.2 等效阻尼系数分析

与线性隔振系统类比，含放大机构隔振系统的等效阻尼恢复力为

(22)

(23)

式中cd为含放大机构隔振器的等效阻尼系数. 由式(23)可以看出，等效阻尼系数是以x为变量的二次函数，因此不再分析x对等效阻尼系数的影响，仅对设计参数θi和c进行分析. 暂定，θi范围为[30°,60°]，阻尼系数c范围为[1 N·s/m,9 N·s/m]，由式(23)即可给出隔振系统等效阻尼随θi、c的变化规律.

3 隔振效果

3.1 频域隔振效果评估

为了验证含放大机构隔振器的隔振效果，与常规线性隔振器对比. 其中，隔振器的设计参数和激励条件相同，采用绝对位移传递率作为指标. 对于常规线性隔振器而言，容易得到其绝对位移传递率的传递率曲线，而对于含放大机构隔振器的惯性质量的绝对位移可由谐波叠加的方式求得：

(24)

得到含放大机构隔振器的绝对位移传递率为

Td=s/z0

(25)

由式(25)可得到含放大机构隔振器的绝对位移传递率曲线Ω-T. 同时，为了验证含放大机构隔振器解析解的正确性，利用龙格库塔法给出部分频点的时域解.

暂定，含放大机构隔振器的初始设计参数为ξ=0.05，θi=60°，z0=0.01，γ=0.02. 分别得到常规线性隔振器和含放大机构隔振器的绝对位移传递率曲线如图2所示.

由图2可见，含放大机构隔振器的数值解和解析结果良好一致,证明其频域解析结果有效. 与常规线性隔振器相比，绝对位移传递率曲线峰值得到显著衰减，且峰值频率略微向高频移动，由此说明含放大机构隔振器实现了对刚度和阻尼放大的设计目标,在系统刚度放大的同时实现了高阻尼输出.

图2 不同隔振器绝对位移传递率曲线Fig.2 Absolute displacement transfer rate curve of different vibration isolators

3.2 时域隔振效果评估

为了进一步对该隔振器的隔振性能进行评估，以下在时域对隔振器的隔振效果进行分析. 具体计算过程：首先，对隔振系统的运动微分方程引入状态变量，将其化简为一阶微分方程组；然后，采用四阶龙格-库塔法进行数值计算即可得到隔振器各部分的时域响应位移和速度；最后，根据隔振系统的动力学关系即可推导出惯性质量的绝对位移的时域响应曲线.

实际中，环境激励呈现宽频特性，为了评估隔振器在宽频激励下的隔振效果，在低频、中频段和高频段各取3个频点，假设隔振器所受位移激励为

Z=0.001(sin 0.1ωnt+sin 0.2ωnt+sin 0.3ωnt+

sin 0.8ωnt+sin 1.2ωnt+sin 1.4ωnt+sin 30.8ωnt+

sin 40.4ωnt+sin 50.2ωnt)

ωn为隔振系统固有频率. 多频位移激励下不同隔振器惯性质量的绝对位移如图3所示. 可以看出，含放大机构隔振器惯性质量的绝对位移幅值较之常规线性隔振器得到明显衰减，说明该隔振器对多频宽频激励的控制效果明显优于常规线性隔振器.

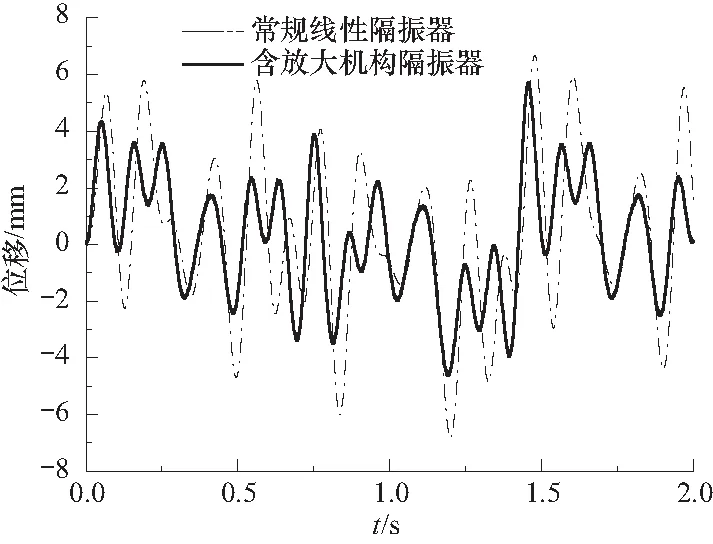
图3 多频稳态激励传递的位移Fig.3 Displacement of multi-frequency steady-state excitation transmission

4 设计参数影响分析

根据第2节所述内容，含放大机构隔振器的主要设计参数为γ、θi和ξ，以下重点讨论这些设计参数对含放大机构隔振器动态特性的影响. 为了便于讨论，以第3节中定义的设计参数为初始值.

4.1 阻尼比ξ 和刚度比γ对隔振性能的影响

绝对位移传递率曲线如图4所示. 由图可见，阻尼系数主要对位移传递峰值有影响，即：随着阻尼系数增大，绝对位移传递率峰值被显著减小；同时，峰值频率基本没有变化，即系统刚度并没有损失. 含放大机构隔振器刚度比对绝对位移传递率曲线的影响如图5所示.可见，刚度比增大，绝对位移传递率峰值逐渐增大；同时，谐振频率向高频移动. 随着频率增加，在高频范围刚度比对隔振系统的传递特性影响趋于一致.

图4 不同阻尼比ξ对应的绝对位移传递率Fig.4 Absolute displacement transfer rate ξ corresponding to different damping ratios

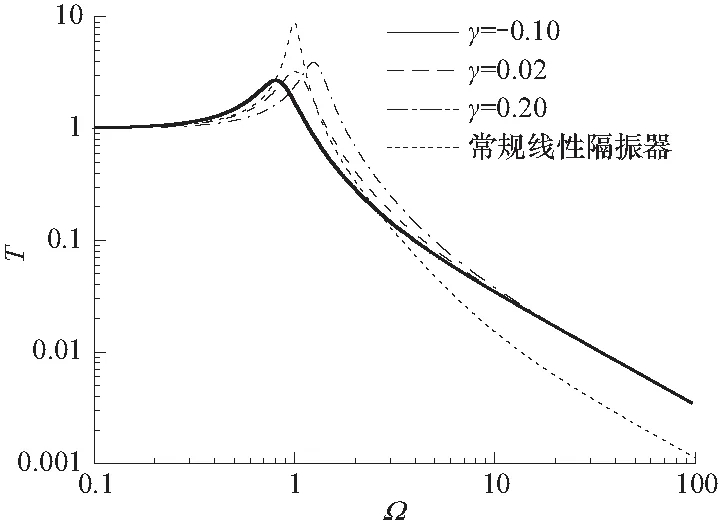
图5 不同刚比γ对应绝对位移传递率Fig.5 Different rigid ratios γ corresponding to absolute displacement transfer rates

4.2 初始倾角值θi 对隔振性能的影响

含放大机构隔振器四端铰接杆初始倾角θi对绝对位移传递率的影响如图6所示. 由图6可见，初始倾角分别为30°、50°和70°时，随着初始倾角增大，绝对位移传递率峰值减小，谐振频率略微向高频移动. 在高频范围，随着初始倾角减小而传递曲线衰减率得到显著改善.

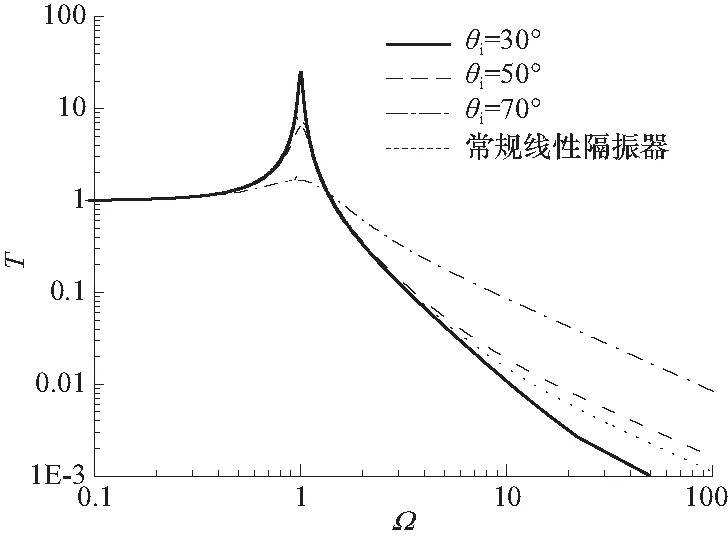
图6 不同初始倾角值对应的绝对位移传递率Fig.6 Absolute displacement transfer rate corresponding to different initial inclination values

5 试验验证

为了验证解析模型的正确性，加工与解析模型等效的试验件如图7所示. 其中，惯性质量m=2.2 kg；杆长l=0.15 m；初始倾角θi=60°；垂向弹簧刚度kv=6 700 N/m；水平弹簧刚度kh=2 300 N/m. 需要说明的是，隔振系统中阻尼部分主要为各部件之间相对运动产生的摩擦阻尼、结构材料阻尼和空气阻尼.

图7 试验件Fig.7 Test sample

试验测试系统主要包括：激振器、信号采集仪、信号发生器、功率放大器、计算机. 试验状态如图8所示，激振器在试验件底部施加激励，模拟解析模型中的位移激励，图中的泡沫用于抵消试验件自身的重力. 在试验件的上部和底部分别连接一加速度传感器，分别检测输入与输出的加速度，对所检测的加速度进行二次积分后，即可得到输入与输出位移. 设置数据采集仪采样频率为56 Hz，设置信号发生器的下限频率为5 Hz、上限频率为100 Hz，采用线性扫频，扫频时间为60 s. 试验所得传递率曲线与解析所得传递率曲线对比如图9所示. 在图9中，两条传递率曲线谐振频率约为12 Hz，谐振峰值约为2.5. 可以看出，解析所得结果与试验所得结果总体趋势基本一致. 但是在共振点附近的频段内，解析曲线与试验曲线拟合有误差. 产生误差的原因有①在进行实验时，为了保证实验件的自由状态，实验件在泡沫上放置，未做其他的固定措施参见图8，导致实验件安装状态不稳定；②为了约束实验件上下两个板在垂向的运动，在上板安装一直线轴承. 但在实验时，上下两个板由于加工误差及直线轴承的安装误差较大，不能严格按照直线运动，所以会导致直线轴承产生的摩擦力较大.

图8 试验状态Fig.8 Test status

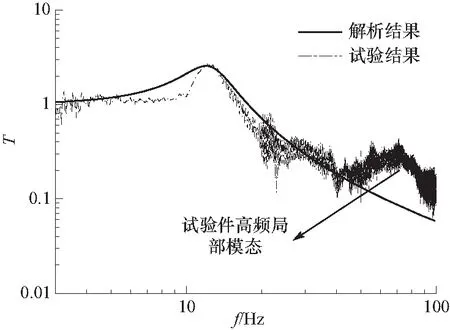
图9 试验与解析传递率曲线对比Fig.9 Comparison of test and analytical transfer rate curves

上述两种情况均会导致在实测结果出现误差，导致隔振器位移响应不稳定，进而使实验所得传递率曲线与理论曲线存在误差. 但是，就整个计算频段而言，解析曲线和实验曲线总体变化趋势一致，所以不影响验证本文所建理论模型有效性及分析结果正确性. 在高频段，试验所得传递率曲线出现波动，该波动是由试验件高频局部模态所致，由于隔振系统解析结果主要用于表征系统在中低频段的减隔振效果，不包含高频模态的影响，所以文中由高频局部模态引起的动态响应不再做讨论.

6 结 论

提出一种含放大机构的隔振器，在所建隔振系统动位移学方程基础上，采用谐波平衡法给出其幅频响应和相频响应的解析表达式. 然后，分别给出该隔振系统的等效刚度和等效阻尼表达式. 分别在时域和频域对含放大机构隔振器的隔振效果进行了评估. 最后，采用绝对位移传递率作为评价指标，对其关键设计参数进行了影响研究. 计算结果表明：

① 与常规线性隔振器相比，通过研究含放大机构隔振系统的等效阻尼和等效刚度得到，在隔振系统刚度不损失的条件下，显著增大了系统的输出阻尼；

② 在时域采用多频谐波激励，计算发现，相比常规线性隔振器，含放大机构隔振器可大幅度衰减传传递到惯性质量的位移；

③ 隔振器阻尼比ξ增大，绝对位移传递率峰值均减小，谐振频率基本没有变化；

④ 隔振器刚度比γ增大，绝对位移传递率峰值逐渐增大；同时，谐振频率向高频移动. 而在高频范围刚度比对隔振系统的传递特性影响趋于一致；

⑤ 初始倾角θi增大，绝对位移传递率峰值减小，谐振频率略微向高频移动；

⑥ 通过实验验证，证明所建解析模型和表达式正确有效；

相关研究成果对含放大机构隔振器的设计和应用均具有一定的理论指导意义和工程参考价值.