二维不平度路面的空间域滤波重构及仿真
王汉平, 张哲, 张宝振
(北京理工大学 宇航学院,北京 100081)
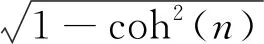
1 路面不平度的滤波重构法
路面不平度常被假设为一均值为0、不同截面具有相同统计方差的平稳随机过程. 国标GB/T 7031-2005用功率谱密度函数(PSD)来表达其不平度状况,PSD表达式为
(1)
式中:n∈(n1,n2)=[0.011,2.83]m-1,为空间频率;n0为参考空间频率,通常取0.1m-1;Gq(n0)为参考空间频率下的路面不平度系数,路面按好坏等级分为A~H共8级,路面等级不同,其取值也不相同;w为频率指数,一般取2.
引入截止空间频率n1来构造稳定的动态滤波系统,以确保在白噪声激励下响应量的功率谱特性能与标准路面谱逼近[7],即
(2)
式中:空间圆频率Ω=2πn;j为虚数. 最终,反演出单轮辙空间域路面不平度的白噪声滤波方程(路面不平度生成模型)为
(3)
2 基于轮辙功率谱密度阵LU分解的模拟算法
双轮辙不平度的功率谱矩阵为[10]
(4)
相干函数coh(n)的定义为
(5)
经过大量试验给出了一种描述不同路面和轮距的路面不平度相干函数[11-12]
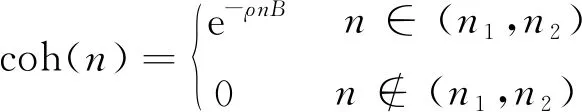
(6)
式中:B为左右轮的轮距;ρ为跟路面有关的经验值,由此可知coh(n)∈[0,1]. 所以式(4)中的功率谱矩阵可进行LU分解,即分解为一个下三角矩阵与其转置的乘积,形如:G(n)=Η(n)HT(n),其一个特解为
(7)
于是,可以构造两个相互独立、谱值为1的白噪声w1(x)、w2(x),其对应的傅里叶变换为W1(n)、W2(n),则左右轮辙不平度与两个白噪声之间满足传递函数为[H(n)]的传递关系,即:
(8)
于是,对式(8)中的QL(n)进行空间域白噪声滤波转化,即为
(9)

(10)


(11)
式(10)和式(11)两式均能保证其特征方程的根值在左半S平面(见表1),也就是能保证系统的稳定性.



特征根阶次coh(n)展开1-coh2(n)展开1-8.50 +1.74j-4.7432-8.50 -1.74j-1.2273-7.47 +5.25j-0.4144-7.47 -5.25j-0.1645-5.03 +8.99j-0.0586-5.03 -8.99j-0.0137—-0.939+2.84j8—-0.939- 2.84j
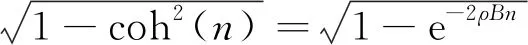

图1 相干函数coh(n)及其P(6,6)阶Pade展开曲线的对比Fig. 1 Coherence function coh(n) vs its P(6,6) Pade expansion

图2 函数及其P(8,8)阶Chebyshev-Pade展开的对比 vs its P(8,8)Chebyshev-Pade expansion
3 路面生成及结果检验
式(8)(10)及(11)的组合,就是路面不平度的空间域滤波模拟模型,利用Matlab对表达模型的常微分方程组编写了路面不平度曲面生成程序,对不同等级路面进行了大量的仿真验证,模拟所得的路面功率谱与标准谱吻合良好,左右轮相干性与参考函数也具有较好的一致性. 篇幅所限,在此不便一一列出,而仅就ρ=1时的D级路面,即:Gq(n0)=1 024×10-6(m2/m-1)的仿真情况进行展示. 图3所示路面纵向长度L=2 000 m,轮辙距离B=5.0 m,路面等级为D级,空间频率范围从0.011~2.83 m-1,垂向偏移为0的两方法生成的两轮辙路面不平度曲线. 从中不难看出路面不平度整体上的波动特性,而且在整体波动的基础上,还附带有更高频的扰动.

图3 D级路面的模拟随机路面不平度(B=5.0 m,ρ=1)Fig.3 Simulated road profiles of D-grade road(B=5.0 m,ρ=1)
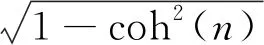
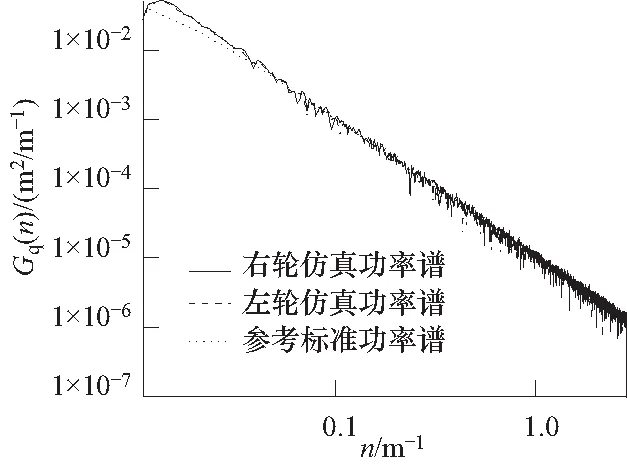
图4 D级路面左右轮路面不平度功率谱密度函数对比Fig.4 Simulated PSD of D-grade road roughness for left and right tracks

图5 D级路面左右轮路面不平度相干性对比Fig.5 Coherence of D-grade road roughness for left and right tracks
图6模拟的宽度为5 m,ρ=1的路面的不平度表面,由此可见,模型对于构造二维的任意宽度的路面不平度表面均具有较好的适应性.

图6 D级路面不平度路面仿真结果Fig.6 Simulation road surface of D-grade road
4 结 论
为保证稳定性,采用截止空间频率重构了传递函数,即路面不平度的白噪声滤波方法;基于双轮辙功率谱密度阵的LU分解得到了白噪声滤波传递函数阵的解析表达,对传递函数阵中所涉及的相干函数直接采用Pade展开,对涉及相干函数的复杂超越函数使用Chebyshev-Pade展开,实现了白噪声滤波传递函数的高效率、高精度的有理化;路面不平度的仿真结果表明,各轮辙的自功率谱与标准功率谱吻合较好,轮辙间的相干性也与参考模型也具有较好的一致性,从而验证了基于功率谱密度阵LU分解所得到的白噪声滤波传递函数及其超越函数的Pade展开、Chebyshev-Pade展开近似处理方法具有较高的数值可信度,能较好地用于二维路面不平度的模拟,并具有较高的计算效率. 空间域路面不平度的模拟表明,不同轮辙的功率谱密度函数、相干函数均与标准函数吻合较好,这验证了所建模型的可信性及仿真方法的有效性,为车辆路面运输动力学仿真的空间域路面建模提供了一种高效、可信的方法.

