基于数形结合思想，促进思维能力发展

陈琴兰

一、案例主题

数形结合思想在“分数乘分数”算法与算理中的应用，促进思维能力发展。

二、数形结合思想内涵阐述

数形结合是一种重要数学思维方法，就是把题目中抽象化的数学语言，转化为学生比较容易理解而且生动形象的图形，学生更容易理解题目。至此，借助抽象思维与形象思维结合，使呈现的复杂问题简单化、抽象问题具体化，促进学生解决问题的有效方法，实现学生优化解题策略的目的。小学生的思维是从具体形象思维为主要形式逐步向抽象逻辑思维过渡，但这时逻辑思维是初步的，且在很大程度上仍具有的形象性。数形结合不仅满足教育的需要，更是为了满足小学生数学思维发展的需要，促进学生数学思维的形成，对发展数学思维起到事半功倍的作用。

新教材将计算教学中算理的理解，设计为直观图形感知、抽象图形深化、总结计算方法，其实就是数形结合思想的渗透，此思想在知识形成与问题解决中显示出的直观性、简洁性，为培养学生良好的数学思维品质打下基础。

1.案例描述

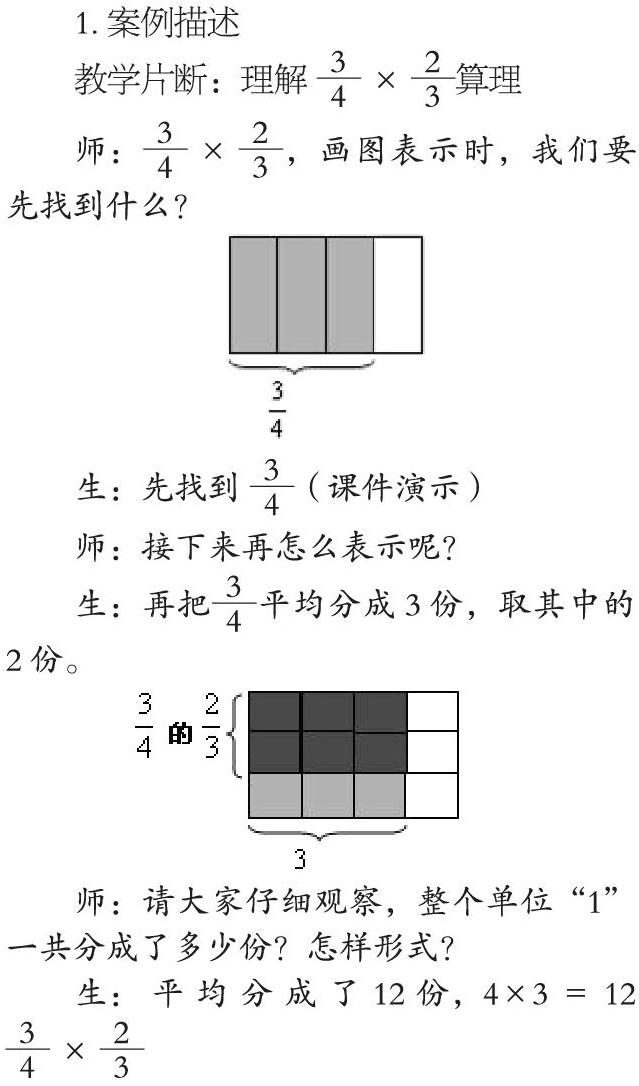
教学片断：理解 ×算理

生：先找到 （课件演示）

师：接下来再怎么表示呢？

生：再把平均分成3份，取其中的2份。

师：请大家仔细观察，整个单位“1”一共分成了多少份？怎样形式？

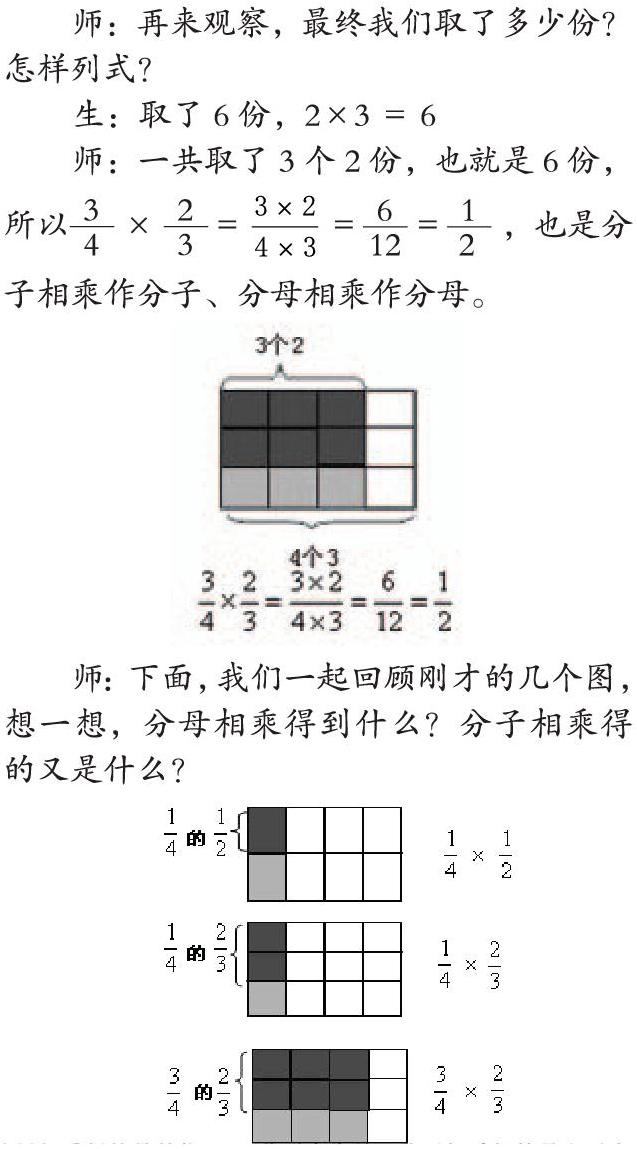
师：再来观察，最终我们取了多少份？怎样列式？

生：取了6份，2×3=6

师：下面，我们一起回顾刚才的几个图，想一想，分母相乘得到什么？分子相乘得的又是什么？

生：分母相乘得的是单位“1”分了多少份，分子相乘得的是取了多少份。也就是分子相乘作分子，分母相乘作分母。

师：完全正确。这就分数乘法的算法。瞧，数形结合不仅帮助我们理解了意义还学会了算法，懂得了算理。

2.案例分析

（1）以“数”想“形”，拓展学生数学思维的广阔性

數学对象是复杂的，它既不像一个球，因为从各个角度观察都是不同形状，也不像一张纸只有一个平面而无层次。因此，数学思维需要有不同的角度和丰富的层次。而“数”和“形”是一种对应，有些数学语言比较抽象，学生难以把握，而图形具有形象、直观的优点，能够主观反映学生思维的过程，起着解决问题的关键性作用，因此，我们可以把“数”对应“形”找出来，利用图形来解决问题。比如：教学中，有些孩子的语言不成熟不善于表达，经常不能准备表述自己的所思所想。以“数”想“形”的方式进行教学，学生的兴趣高，又乐于展示自己思维过程。

以上片断，要理解“分数乘法”的意义比较抽象，学生理解起来不是很容易，所以，利用图形把抽象的问题直观化，对本节课的教学显得尤其重要。在教学过程中，注重运用直观图形，巧妙地把“数”和“形”结合起来，引导学生动手折一折、画一画，把抽象的“分数乘分数”的意义直观化，加之课件直观形象的优势，帮助学生理解其真正的内涵。

（2）以“形”算“数”，拓展学生数学思维的独创性

思维的独创性是人类思维的高级形态，它是指在新异的情境中，在一定目标的指引下，调动一切已知信息，独特、新颖且有价值地解决问题所表现出来的智力品质。

华罗庚先生说过：“数缺形时少直观，形少数时难入微。”他认为仅就数而论，则缺乏直观性;仅就形而论，则缺乏严密性。不少教师认为计算教学简单枯燥，若能够巧妙地用数形结合，由“数”到“形”，再由“形”到“数”，数形相辅。再把抽象的数学语言与直观的图形相结合，抽象思维与形象思维相结合，二者结合可以优势互补，收到事半功倍的效果。“分数乘分数”的计算方法比较简单，但让学生明白怎样得出算法就比较难。以上片断中利用直观图引导学生分一分，不仅理解了算理，而且有效地突破了算法上的难点，使简单枯燥可以转化为“火热的思考”，促进学生思维创造性发展。

（3）“数”“形”联谊，拓展学生数学思维的灵活性

思维的灵活性是指依据客观条件的变化及时调整思维的方向。思维的灵活性表现在不受思维模式和固定模式的束缚，善于发现新的条件和新的因素，在思维受阻时能及时改变原思考路线，修改原定方案，从而找到新的方案与新的途径。

著名数学特级教师徐斌说过：应该给计算教学加点“甜味”，对于算法与算理，学生在理解时总是比较抽象，在这两者之间巧妙地结合，为学生创设一条“思维”之路，让学生充分感受在“数”与“形”相结合之下，擦出思维“火花”，慢慢提升思维的灵活性。比如，“分数乘分数”的算理属于比较难以理解的内容，通过折纸、画图的手段向学生直观地展示运算的过程、本质的变化、结果的产生，让学生“知其然更知其所以然”。算理教学需借助直观，引导学生经历自主探索、充分感悟的过程，将“数”与“形”巧妙地结合在一起，这比空洞的说理、枯燥的训练好多了。

三、结语

数学是一门理性思维的科学，在课堂教学中，作为一线教师要根据学科特点，启迪、培养学生的思维能力，充分展示学生的思维过程，利用“数”与“形”有机结合，在思维的困惑中找到“出路”。在思维过程中既让学生感悟学习数学的乐趣，

又培养学生思维的深度、广度，在此方面是其它学科或其他培养方式所无法比拟的。

在以上这个教学案例中不难看出：“数”与“形互化的过程，既是解题的过程，又是学生的形象思维和抽象思维协同运作、互相促进的过程，从而使教与学更加赶写而巧妙。数形结合就像是给学生在建构知识了一个拐杖，有了这根拐杖，学生形象思维逐渐向抽象思维过渡才能走的更稳、更好，可以使复杂的问题简单化，抽象问题具体化。