基于“雨课堂+Mathematica”的解析几何教学改革探索与实践

李彩娟 王玉磊 苑倩倩

【摘要】本文以“双曲抛物面”的课堂教学为例，借助雨课堂教学平台和Mathematica数学软件等信息化技术手段，就解析几何教学的有效途径进行了初步探究.

【关键词】双曲抛物面;雨课堂;Mathematica

【基金项目】2019年河南省高等教育教学改革研究与实践项目：基于雨课堂的代数与几何课程混合式教学模式研究与实践（2019SJGLX504）;2019年信阳学院教育教学改革研究项目：基于雨课堂的数学基础课程混合式教学模式研究与实践（2019YJG26）;2020年信阳学院教育教学改革研究项目：疫情防控背景下《数学分析》课程线上教学的探索与实践研究（2020YJG025）;

2018年信阳学院校级课题：几类分数阶微分方程边值问题解的存在性研究（2018LYB09）

一、“双曲抛物面”在传统教学中遇到的问题

解析几何是数学专业的“老三基”之一.传统的解析几何课堂教学最主要、最常见的教学模式是“满堂灌”，在这种教学模式下，学生只能是知识的“搬运工”，课堂教学不能真正地釋疑解惑.这种比较常见的教学模式主要体现为教师是教学活动的主体，在整个教学过程中拥有支配权和主导权，学生则是和主体相对立的客体，并没有主动参加教学活动的兴趣.所以，学生的自主学习能力比较差，学习积极性不高，教师也不能及时掌握学生的学习情况，课堂教学效果不好.双曲抛物面是解析几何中最典型的一类二次曲面，是解析几何课程中涉及的空间图形之一，它的方程形式比较简单，所以我们可运用平行截割法从方程入手去研究它的图形.由双曲抛物面的方程来研究它的几何性质并画出图形，正是解析几何的基本思想“利用代数方法来研究几何问题”的直接体现.但是它的图形比较复杂，如果采用传统的手工作图，图形既不准确也不直观，不仅浪费了有限的教学时间，而且对学生的空间想象能力要求较高.所以，大多数学生谈“双曲抛物面”色变，在他们的心目中，“双曲抛物面”是解析几何的难点.

二、基于“雨课堂+Mathematica”的课堂教学案例——双曲抛物面

（一）使用雨课堂

作为一种智慧教学工具，雨课堂将前沿教育理念和互联网技术巧妙融合，科学地覆盖了课前、课中、课后的每一个教学环节，从课前预习、课堂互动、课后作业等方面帮助教师采集课程数据，量化分析学生的学习情况，实现精准教学，为传统课堂教学缺少师生互动提供了完美的解决方案.在雨课堂中，课堂教学互动始终在线，教与学的能量最大限度地释放，学生的学习兴趣得以激发，教育教学效果达到最优.

1.课前准备

教师根据本节课的教学设计将丰富的教学资源插入课件，还可以在幻灯片中配以语音解说，然后将这些课件通过雨课堂推送到学生的微信端.学生可以依据自己的时间灵活地进行课前的自主预习，还可以在遇到问题的内容上点“不懂”，反馈预习效果.因此，教师能够及时了解学生的预习情况，在课堂教学中做到有的放矢.

2.课堂教学

学生通过手机扫码完成课堂签到，极大地弥补了人工考勤费时费力、影响课堂教学进度的不足.教师从日常生活中无处不在的几何形体说起，以多媒体展示我们经常吃的薯片以及2012年伦敦奥运会自行车馆的屋顶等，它们的形状都是双曲抛物面，以此创设情境，激发学生的学习兴趣，引出本节内容.然后，教师给出双曲抛物面的定义并提出问题：双曲抛物面方程能反映出哪些几何性质？我们又该如何得到双曲抛物面的大致图形？学生以小组讨论的方式，思考由方程得到图形的方法.

教师以“切黄瓜”为例形象说明（如图1）：每次刀切下去的时候，刀所在的平面和黄瓜截面的交线就是我们切出来的黄瓜片的边界曲线，这是一条平面曲线，当我们了解了所有黄瓜片的边界曲线的形状和变化趋势后，整根黄瓜的形状是不是就有了？这就是下面我们要用到的平行截割法：用一组平行平面去截割曲面，研究所得到的截痕曲线的变化趋势，再推断出曲面的大致形状.教师让学生以小组讨论的方式，思考如何利用平行截割法得到双曲抛物面的图形.然后，教师通过雨课堂进行点名，指定学生回答小组讨论的结果，提高学生的课堂参与度.学生可以根据自己的观点或对问题的思考进行图文投稿，或将自己的疑问发布弹幕.学生的所有回答会在大屏幕上以无记名的方式横向滚动显示.教师也可以将学生发送的图文内容投放至大屏幕与全班学生共享.因为在大屏幕上不显示回答人的姓名，学生积极主动，答案个性鲜明，课堂气氛活跃，师生互动愉快轻松.这样，教师能够随时了解学生的学习情况，实时调整课堂教学进度.学生成为学习的主动者，学习积极性得以调动，课堂学习效率大大提高，解析几何课堂教学焕发出生机与活力.而且通过雨课堂，整个教学过程都可以记录下来，学生对于课堂上没有听懂的地方，可以课下观看录制的讲解，再现教学过程.

3.课后分析

雨课堂会通过“云计算”向教师提供本节课全周期的数据分析，把所有的教学动作以大数据的形式反馈给教师，实现了课堂数据采集的功能，教师从而能够了解每一名学生的学习情况，更加全面、立体地对学生做出客观的评价.教师还可以根据课堂反馈制作课后复习课件，而后通过手机端雨课堂发布给学生，对学生进行综合考查和测评，巩固本节课的教学内容并进行专业拓展.

（二）将Mathematica引入课堂

解析几何课程中涉及大量的空间图形，传统的手工作图很难让学生对图形有直观的理解，尤其是像双曲抛物面这种比较复杂的曲面.借助Mathematica强大的绘图功能，教师可以将双曲抛物面形象地呈现给学生，加深学生对双曲抛物面的理解和对平行截割法的掌握.

在Mathematica的工作窗口输入以下命令：

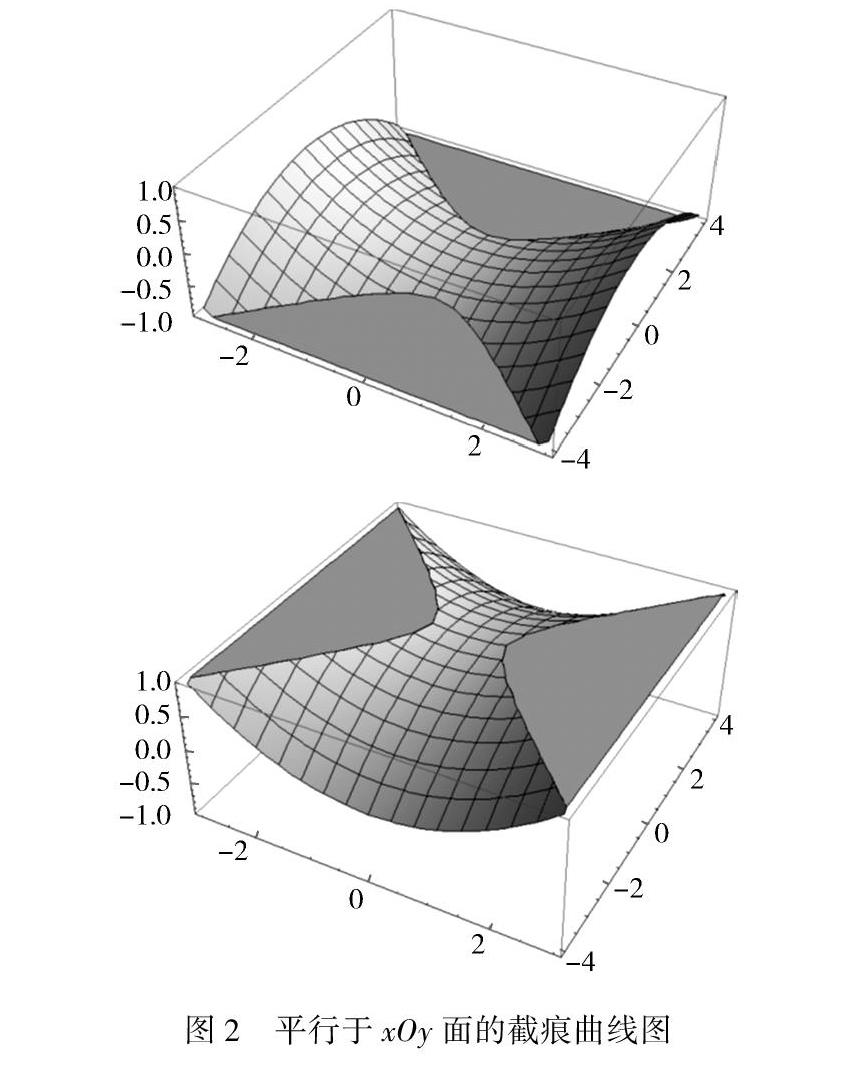
a=Table[Plot3D[x^2/9-y^2/16-z，{x，-3，3}，{y，-4，4}，PlotRange→{-1，1}]，{z，1，-1，-0.05}]

运行后可以得到双曲抛物面平行于xOy面的一系列截痕曲线，选取其中的两幅图片如图2所示.

然后输入命令：

ListAnimate[a]

运行后就得到演示双曲抛物面截痕曲线动态变化过程的动态图.

同样，在Mathematica的工作窗口输入以下命令：

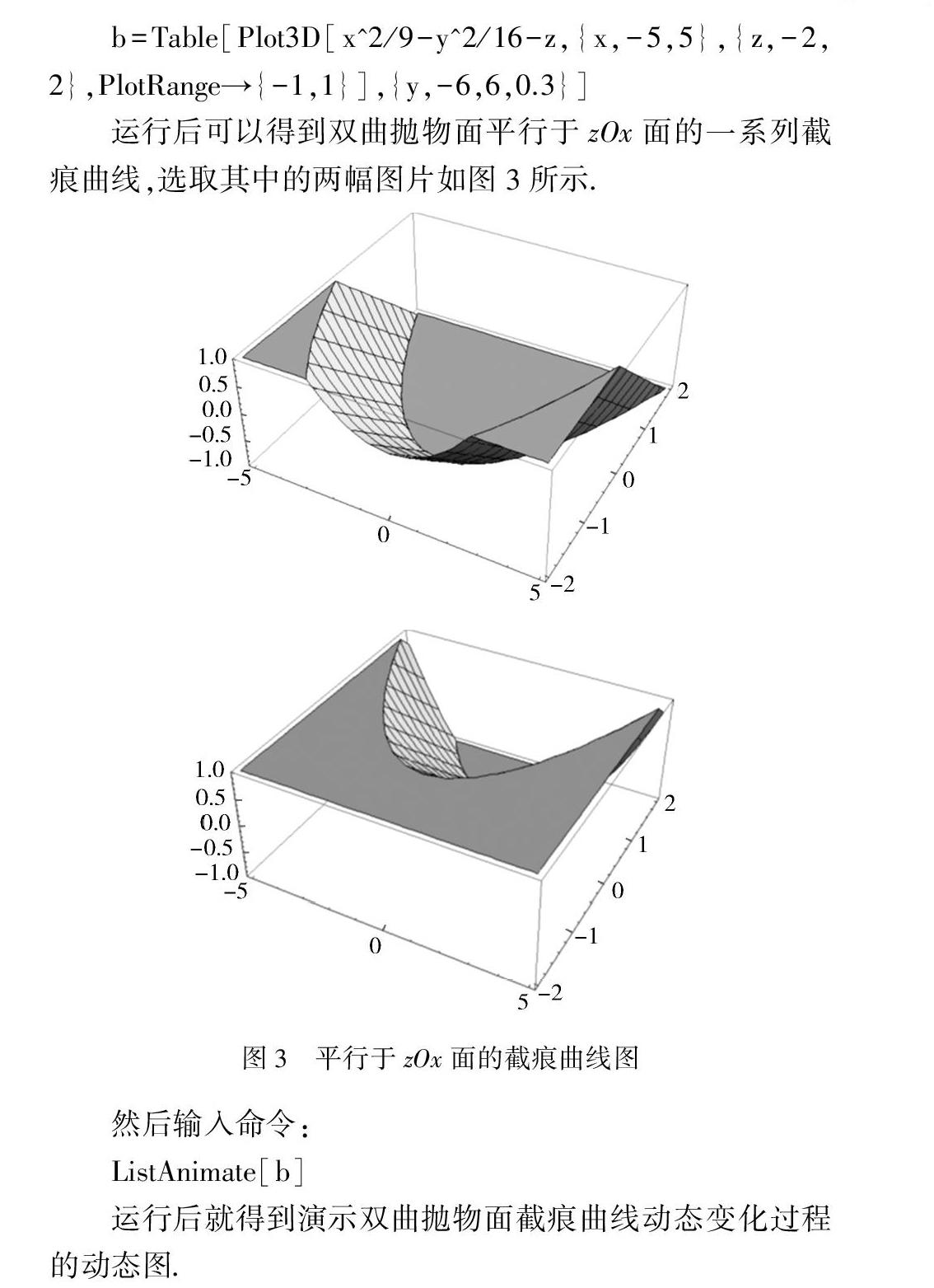
b=Table[Plot3D[x^2/9-y^2/16-z，{x，-5，5}，{z，-2，2}，PlotRange→{-1，1}]，{y，-6，6，0.3}]

运行后可以得到双曲抛物面平行于zOx面的一系列截痕曲线，选取其中的两幅图片如图3所示.

然后输入命令：

ListAnimate[b]

运行后就得到演示双曲抛物面截痕曲线动态变化过程的动态图.

结 语

借助雨课堂可以较为全面地分析学生的学习状况，教师可以随时了解学生在听课过程中对知识的掌握情况，从而及时调整教学方案.每一名学生都可以参与解析几何的课堂教学，每个人都是课堂的主人，学习在轻松愉快的氛围中进行，能极大地激发学生学习的兴趣，教学效果将显著提高.Mathematica可以将抽象的、难以理解的空间图形形象地展示出来，还可以演示曲线变化生成曲面的动态过程，直观性扑面而来，不仅让抽象难懂的空间图形易于被理解和掌握，而且极大地增强了解析几何课堂的趣味性.因此，教师应在双曲抛物面的教学中积极运用“雨课堂+Mathematica”.

【参考文献】

[1]吕林根，许子道.解析几何：第5版[M].北京：高等教育出版社，2019.

[2]刘淑贞，王明宇.“雨课堂”+matlab+flash动画让定积分概念教学妙趣横生[J].教育现代化，2019（32）：75-76，81.

[3]范乐乐，钟华，龙路英.“雨课堂”在高等数学课程大班教学中应用[J].教育现代化，2018（53）：261-263.

[4]张婷.基于信息化的高职数学课堂教学的探索与实践：以“定积分的应用”为例[J].中国新通信，2019（08）：166-167.