含螺栓连接输电铁塔主材的承载性能研究
江文强,陈欣阳,刘景立,牛卓博,冯立言,安利强
(1.华北电力大学河北省电力机械装备健康维护与失效预防重点实验室,河北 保定 071003;2.国网河北省供电公司保定供电分公司,河北 保定 071051)
输电铁塔作为电力系统的重要组成部分,对电网的安全运行起着重要的作用。主材是输电铁塔的主要受力构件之一,通常需要分段连接而成[1],其中,螺栓连接节点对于保障输电铁塔的承载性能非常重要。为了保证主材的强度与刚度,通常需要较多数目的螺栓[2]。输电铁塔外包钢的规格一般大于主材,在螺栓连接处,由于节点上下主材角钢的型号通常不同,从而导致主材轴线并不共线,连接偏心。在轴向载荷作用下,螺栓连接处主材会产生附加弯矩,影响其受力特征。文献[3-4]研究了螺栓节点对杆塔变形的影响,并指出螺栓预紧力减小到一定程度时,螺栓发生滑移,会造成杆塔变形。文献[5]对角钢塔典型节点进行足尺试验研究和有限元分析,指出偏心作用会降低节点板的屈服破坏承载力。以上文献都没有研究螺栓连接对极限承载力的影响。
大量真型塔试验表明,输电铁塔破坏与主材螺栓连接部位失稳有关,有时甚至未达到设计载荷而提前发生主材失稳[6]。图 1 为在某 220 kV ZMC2 型输电铁塔真型塔试验中主材发生的失稳破坏,主材破坏位置距节点较近,主材失稳时施加载荷为设计载荷的95%。

图1 输电铁塔主材失稳破坏Fig.1 Buckling of main leg in transmission tower
由此可见,对含螺栓连接主材的承载性能开展研究显得十分重要。本文以220 kV ZMC2型输电铁塔为研究对象,建立含螺栓连接主材的有限元模型,分析长细比、螺栓大小、螺栓预紧力、螺栓松动个数和主材装配间隙等参数对构件极限承载力的影响规律,从而为输电铁塔结构设计提供理论基础。
1 主材模型
本文针对图1所示输电铁塔破坏位置处进行精细化建模。图2(a)为含螺栓连接的输电铁塔主材模型示意图。其中,主材1为L100×10等边角钢,主材2为L110×10等边角钢,外包钢为L110×10等边角钢,螺栓为6.8级M20×40的标准六角螺栓。外包钢与主材连接所用的螺栓个数为10,呈单排排列,螺栓之间的间距为60 mm。为了便于研究,取主材1的长度为l,主材2的长度为h,外包钢的长度为w,主材与主材之间的装配间隙为j,并对螺栓进行了编号,如图2(b)所示。为分析长细比、螺栓大小、螺栓预紧力、螺栓松动个数和主材装配间隙等对构件极限承载力的影响规律,建立了5类参数化模型。
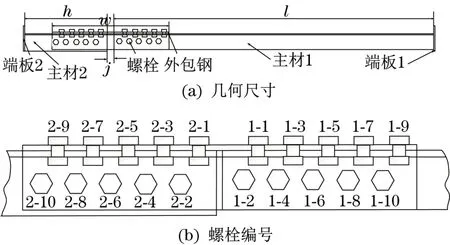
图2 含螺栓连接的输电铁塔主材Fig.2 Transmission tower main leg with bolts
1.1 不同长细比模型
为了研究长细比的影响,分别对主材规格为L100×10 的不含螺栓连接和含螺栓连接的输电铁塔主材进行研究,长细比分别取80、100、120 和140。构件的详细参数如表1所示[7]。
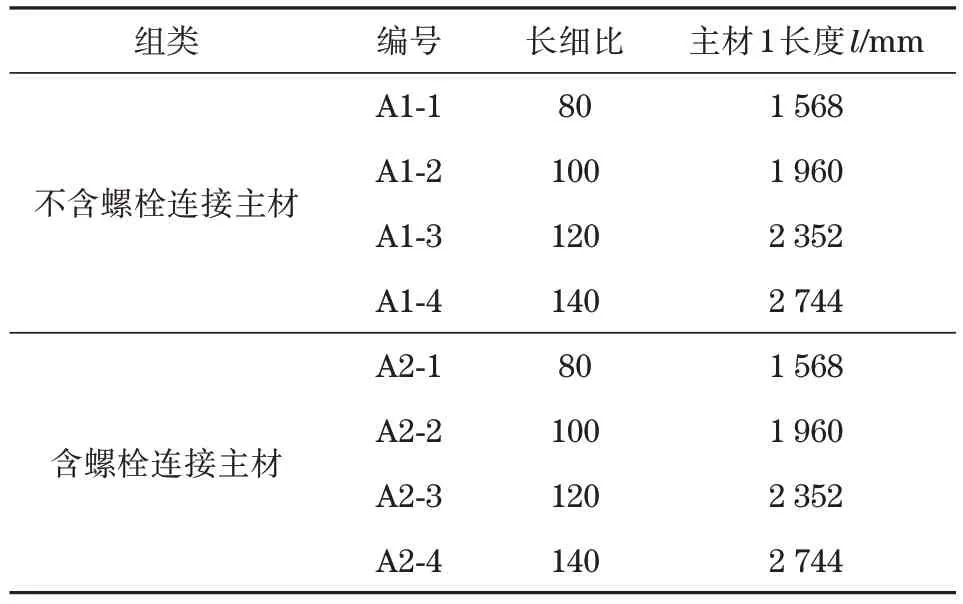
表1 不同长细比模型Tab.1 Models of different slenderness ratio
1.2 不同螺栓直径模型
为了研究螺栓直径的影响,对螺栓直径分别为16、20和24 mm的含螺栓连接的输电铁塔主材进行研究[8],并分别编号为B1、B2和B3。在设计外包钢长度时,保持螺栓间距恒为60 mm,具体参数如表2所示。

表2 不同螺栓直径模型Tab.2 Models of different bolt diameter
1.3 不同螺栓预紧力模型
为了研究螺栓预紧力的影响(本文选取6.8级M20螺栓,其极限承载力为150.8 kN),预紧力分别取其极限承载力S0的20%、40%、60%和80%,并分别编号为 C1、C2、C3 和C4,具体参数如表3 所示。
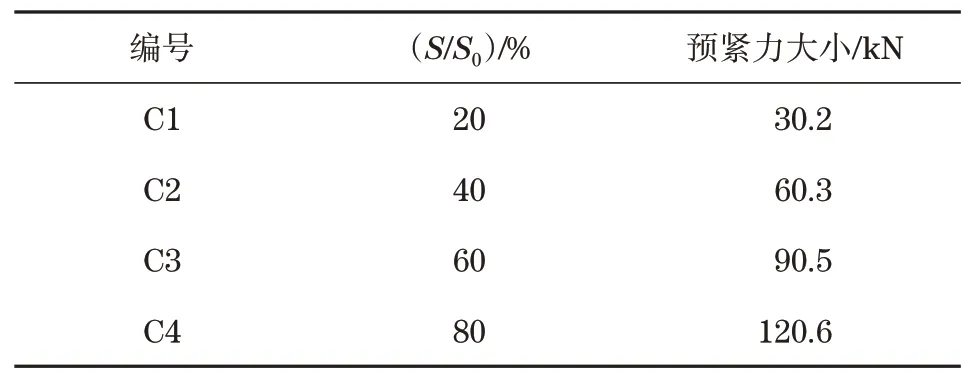
表3 不同螺栓预紧力模型Tab.3 Models of different bolt preload
1.4 不同螺栓松动个数模型
当输电铁塔长时间运行后,螺栓会松动、疲劳,螺栓上的预紧力会减小甚至消失[9]。因此,本文将丧失预紧力的螺栓去掉,仅考虑主材1 上的螺栓出现松动情况,并将模型分为3 组:第1 组模型主材1上的螺栓松动个数为标准构件的40%;第2 组模型为标准构件的60%;第3 组模型为标准构件的80%。将螺栓未发生松动的原模型、第1组模型、第2组模型和第3组模型分别编号为D1、D2、D3和D4,具体参数如表4所示。
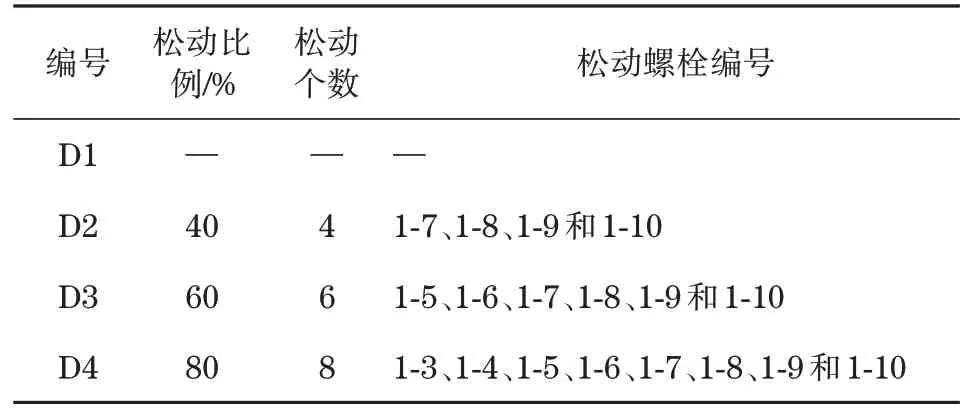
表4 不同螺栓松动个数模型Tab.4 Models of different bolt looseness
1.5 不同装配间隙模型
主材与主材之间进行装配时,主材端部位置通常会有一定的装配间隙,如图2(a)所示。为了研究装配间隙对构件承载力的影响,装配间隙j分别取为0、10、40和60 mm,编号为E1、E2、E3和E4。其中,最大装配间隙取为标准间隙的6倍,具体参数如表5所示。

表5 不同装配间隙模型Tab.5 Models of different assembly clearance
2 有限元模型建立
本文在建模时应用ABAQUS 软件,模型采用C3D8R单元,应用弹性-强化二折线材料模型。主材、外包钢和端板材料均为Q345。Q345 的弹性模量为206 GPa,泊松比为0.3,屈服强度为345 MPa。6.8级M20螺栓的弹性模量为206 GPa,泊松比为0.3,屈服强度为480 MPa[10-11],极限承载力为150.8 kN,本文螺栓预紧力取极限承载力的60%。图3 为所建立的有限元模型,模型约束条件为:在端板2 上,完全约束位于角钢最小轴处的节点;在端板1上,约束位于角钢最小轴处节点X、Y方向的位移,并在角钢形心节点Z方向施加位移载荷。本文取线性屈曲模态变形结果的1/1 000作为初始缺陷,然后对构件进行非线性屈曲分析[12]。

图3 有限元模型Fig.3 Finite element model
3 有限元模拟结果
图4 为构件的应力云图。对比图1 和图4 可以发现,构件的变形与输电铁塔真型塔试验中主材变形大致相同,且最大应力出现在屈曲部位,最大应力为345 MPa。

图4 构件应力云图Fig.4 Component stress
为了研究长细比对构件影响的载荷变形过程,提取端板1 处的载荷变形曲线,结果如图5 所示。图中,横坐标表示端板1 部位最小轴处的Z向位移量,纵坐标为构件的轴压载荷。
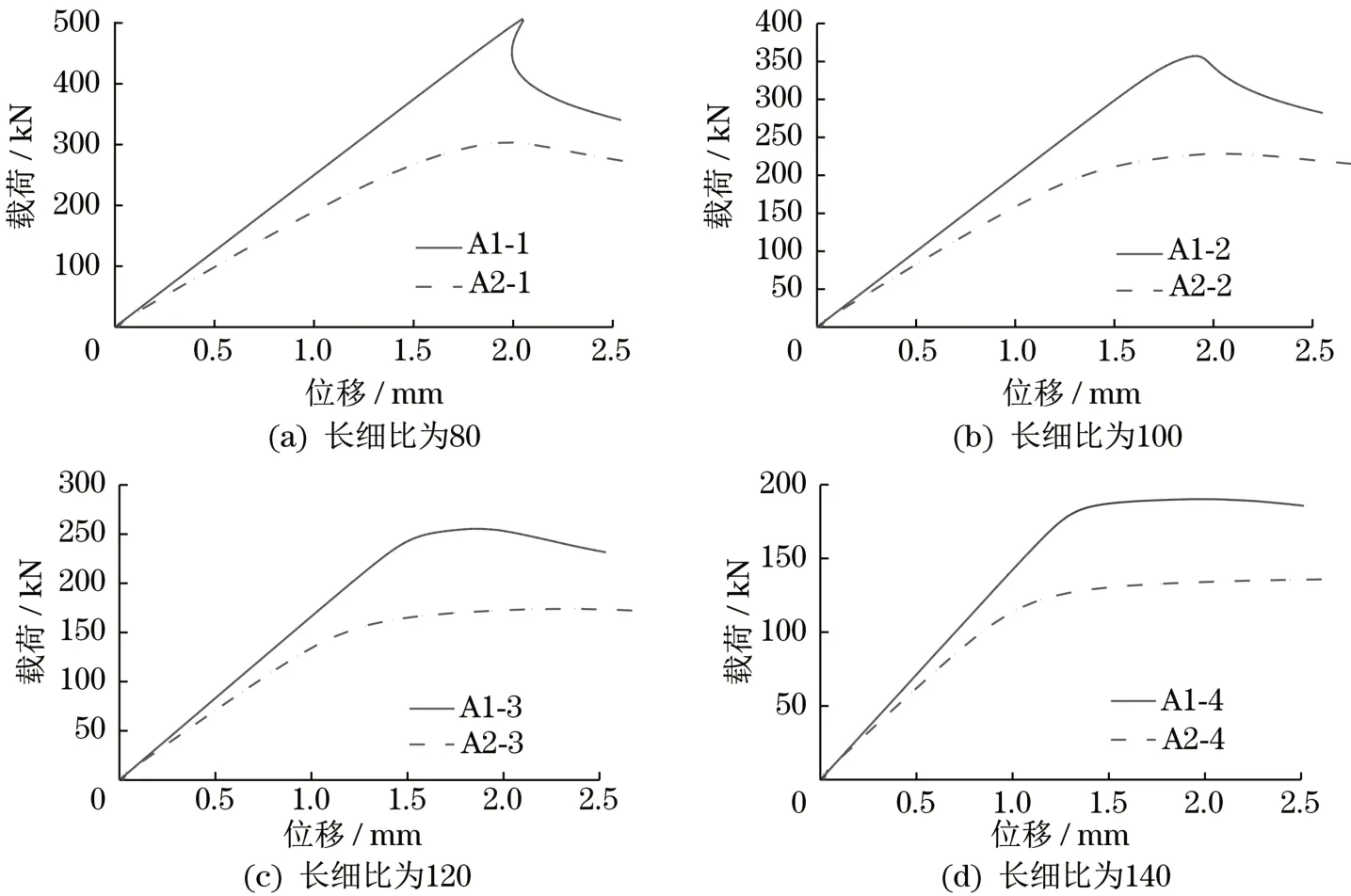
图5 不同长细比模型的载荷-位移曲线Fig.5 Load-displacement curves of models with different slenderness ratios
3.1 长细比的影响
为研究长细比对含螺栓连接的输电铁塔主材极限承载力的影响规律,将图5 中不同长细比模型的极限承载力进行统计,如表6 所示。表中可见:不含螺栓连接主材的长细比为80、100、120 和140时,构件的极限承载力分别为506、357、255 和190 kN,随着长细比的增加,不含螺栓和含螺栓连接的主材极限承载力都逐渐减小;含螺栓连接主材的长细比为80、100、120和140时,构件的极限承载力分别为303、229、174 和135 kN,随着主材长细比的增加,构件极限承载力也逐渐减小,含螺栓连接主材极限承载力的变化规律与不含螺栓连接主材相同。长细比相同时,含螺栓连接主材极限承载力与不含螺栓连接主材构件的极限承载力比值分别为59.9%、64.0%、68.2%和71.1%。由此可知,螺栓连接的存在,使主材极限承载力相对于不含螺栓连接主材平均下降了约35%,且长细比越小,主材极限承载力下降幅度越大。
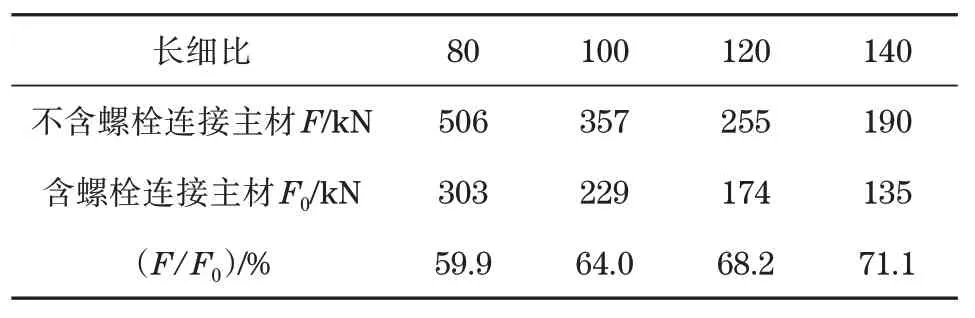
表6 不同长细比模型极限承载力统计表Tab.6 Statistical table of ultimate bearing capacity of different slenderness ratio models
3.2 螺栓直径的影响
图6 所示为 B1、B2 和 B3 模型,分别为螺栓大小M16、M20 和M24 时计算得到的主材构件载荷-位移曲线。以编号为B2 的模型为参考,M20 螺栓个数为10,外包钢长度为670 mm,构件的极限承载力为229 kN;在编号为B1的模型中,M16螺栓个数为16,外包钢长度为826 mm,构件的极限承载力为233 kN,构件极限承载力相对于标准构件仅提高了1.7%;在编号为B3 的模型中,M24 螺栓个数为8,外包钢长度为656 mm,构件的极限承载力为229 kN,构件极限承载力相对于标准构件基本保持不变。由此可见,对于常用的输电铁塔螺栓,其直径对构件的极限承载力影响很小。
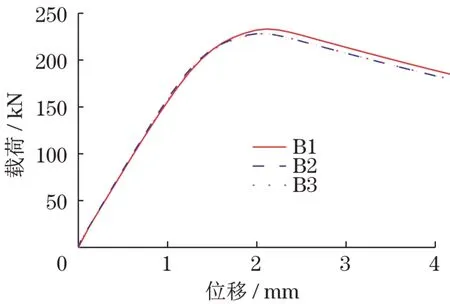
图6 不同螺栓直径模型的载荷-位移曲线Fig.6 Load-displacement curves with different bolt diameters
3.3 螺栓预紧力的影响
图7所示为C1、C2、C3和C4模型,分别为螺栓极限承载力的20%、40%、60%和80%时计算得到的主材构件载荷-位移曲线。图中可知:预紧力分别为螺栓极限承载力的40%、60%和80%时,载荷-位移曲线基本重合,构件极限承载力均为229 kN;预紧力为螺栓极限承载力的20%时,构件极限承载力为227 kN,相对于标准构件仅下降了0.8%。因此,在一定范围内变化时,螺栓预紧力大小对构件极限承载力影响很小。预紧力为螺栓极限承载力的20%时,螺栓出现了滑移现象,滑移距离约为2 mm。若螺栓滑移距离过大,螺栓的螺杆将会与外包钢发生接触,螺栓和外包钢的应力可能都会增大。螺杆与螺孔内壁接触,螺杆受剪切作用,容易出现应力集中现象。预紧力增大到螺栓极限承载力的40%时,螺栓滑移现象消失。因此,增大螺栓预紧力可以有效减少螺栓滑移,从而避免出现应力集中现象。
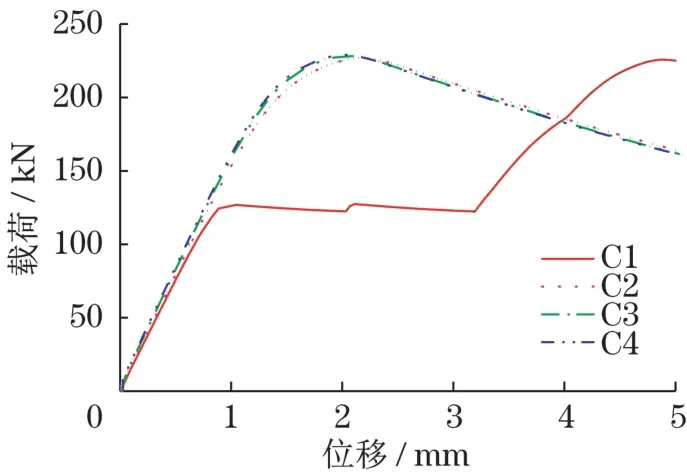
图7 不同螺栓预紧力模型的载荷-位移曲线Fig.7 Load-displacement curves with different bolt preload
3.4 螺栓松动个数的影响
图8所示为D1、D2、D3和D4模型,分别为螺栓松动个数为0、4、6 和8 时计算得到的主材构件载荷-位移曲线。

图8 不同螺栓松动个数模型的载荷-位移曲线Fig.8 Load-displacement curves with different number of bolt looseness
从图8 中可以看出:螺栓松动比例为40%时,与参考模型(螺栓未发生松动模型)载荷-位移曲线基本重合,构件极限承载力均约为229 kN,即构件的强度和刚度均未产生变化;螺栓松动比例为60%时,此时出现了较为明显螺栓连接滑移现象(对应载荷约为170 kN),构件极限承载力为210 kN,构件的极限承载力相对于参考模型下降了约7.8%;螺栓松动比例为80%时,也出现了明显的螺栓连接滑移现象(对应载荷约为72 kN),构件极限承载力为190 kN,构件的极限承载力相对于参考模型下降了约17%。因此,螺栓松动比例为40%以内时,对主材极限承载力影响不大;螺栓松动个数超过40%时,随着螺栓松动比例的增加,主材极限承载力逐渐减小。
3.5 主材装配间隙的影响
图9 为 E1、E2、E3 和 E4 模型,分别为主材装配间隙为 0、10、40 和 60 mm 时计算得到的主材构件载荷-位移曲线。图中可知,不同载荷-位移曲线的斜率和极限载荷略有不同,说明主材的装配间隙大小对构件的刚度以及极限载荷略有影响。随着装配间隙从0 mm 逐渐增大为60 mm,构件的载荷-位移曲线斜率略有减小,这说明主材与主材的装配间隙的不断增大,整个主材连接构件的刚度随之有所下降。装配间隙为0、10、40 和60 mm 时,对应的构件极限承载力分别为238、229、225 和220 kN,构件极限承载力相对于参考模型变化幅度约为3.9%、0、1.7%和3.9%。装配间隙取为标准间隙的6 倍时,构件极限承载力仅下降了3.9%,说明主材装配间隙对主材极限承载力影响较小。
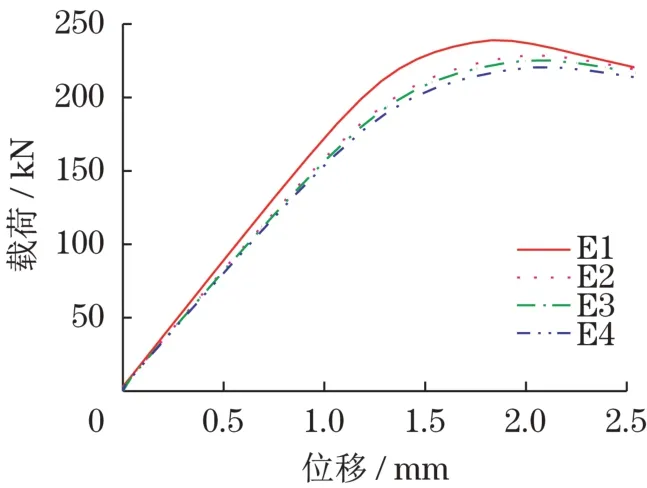
图9 不同主材装配间隙模型的载荷-位移曲线Fig.9 Load-displacement curves with different main material assembly gap
4 结论
输电铁塔主材与主材之间通过螺栓节点进行连接,为了保障输电铁塔有良好的承载性能,对含螺栓连接的输电铁塔主材进行研究尤为重要。本文针对220 kV ZMC2型输电铁塔,分析不同参数对含螺栓连接主材极限承载力的影响规律,得到如下结论:①由于螺栓连接的存在,含螺栓连接主材极限承载力相对于不含螺栓连接主材下降约35%,且长细比越小,主材极限承载力下降幅度越大。②螺栓松动个数为40%以内时,对主材极限承载力影响很小;螺栓松动个数超过40%时,随着螺栓松动个数的增加,主材极限承载力逐渐减小。③螺栓大小、螺栓预紧力和主材装配间隙对含螺栓连接的输电铁塔主材极限承载力影响很小。

