一种基于侦测合一阵列的短波多径信号测向方法

王艳温 易卫明

(1.中国电子科技集团公司第五十四研究所 石家庄 050081；2.75775部队，昆明 65000)

0 引言

如今短波侦测系统体系架构中，短波侦察阵地和测向阵地分离，分别实现侦察和测向，不能实现侦测合一，而在短波新体制侦测合一系统中，采用水平对数周期天线组成有向圆阵，实现全向的侦测合一。短波信号经过电离层反射后形成极化状态不断变化的椭圆极化波，在到达天线阵时会存在水平极化和垂直极化两种电场分量，对于水平极化天线组成的有向圆阵，除了接收水平极化的电场分量之外，还会接收垂直极化的电场分量。在水平对数周期天线的边射方向上，天线接收的水平极化分量最强，而垂直极化分量为0。在天线的端射方向上，水平极化场为0，垂直极化最大，其他方向上两种极化分量都有，因此水平对数周期天线组成有向圆阵是极化敏感阵列[1-3]。短波信号通过电离层传输到达接收端，接收数据是多径传播信号的混合信号，并且极化敏感有向阵列每个接收单元接收信号的极化分量各不同，因此传统的测向方法是失效的，需要研究针对极化敏感有向阵列的短波多径信号测向[4-6]新方法是非常必要的，对于实现短波新体制侦测合一系统的效能发挥具有重要的军事意义。

1 侦测合一阵列结构特性及接收模型

侦测合一阵列由水平对数周期天线组成，为内向异构阵列，等效相位中心随频率变化，阵列结构如图1所示。

图1 侦测合一阵列结构

侦测合一阵列利用水平对数周期天线的有向性实现高灵敏度侦收和测向，但用于测向的有效单元个数有限，有效孔径较小。侦测合一阵列与大基础测向阵列具有较大的差异，如表1所示。

表1 侦测合一阵列与大基础测向阵列对比

xi(t)=Ai(k)·u*s(t)+n(t)

(1)

其中，Ai(k)称为天线的响应，包含了幅度因子和相位因子，u*为来波的极化状态。在球坐标下，远场的A(k)没有纵向分量，只有横向分量。把A(k)在波前面上分解为两个标量

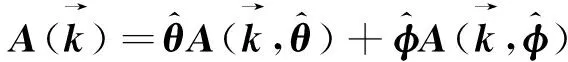
(2)

(3)

两个场分量的幅度分别为|Aθ(k)|，|Aφ(k)| 代表两个场分量的幅度方向图。对Aθ(k)、Aφ(k)取相位，对应两个场分量的相位方向图。

2 极化似然测向算法

由以上分析可知，传统的测向方法[8]已不再适用于侦测合一阵列，文献[7-17]提出的针对极化敏感阵列的测向方法大多适用于独立信号，在短波多径环境下测向性能会急剧下降，基于以上侦测合一阵列的接收模型，本文提出了一种极化似然测向方法，可同时解决侦测合一阵列的极化敏感特性和短波传输的多径特性。

贝叶斯方法[18-20]是基于统计理论的一种经典方法，适合于有关参数估计问题。最大似然(ML)估计方法就是贝叶斯估计方法的一种特例，是在已知白噪声情况下的贝叶斯最优估计。在ML算法中，观测所得信号的似然函数被定义为含有未知参数的条件概率密度函数，目的是选定未知的参数以使得该似然函数尽可能大。通过最大化似然函数求出的解都被认为是未知参数的一个估计。

考虑天线阵由p个阵元组成，其中每个阵元包含两个不同极化的天线。这p个阵元的摆放位置和朝向是任意的。假设有q个窄带信号入射到天线阵，它们的极化矢量分别为γ1,…,γq，中心频率为ω0，入射方向为θ1,…,θq。

天线阵接收的信号可以用复包络表示为

(4)

其中x(t)和n(t)是2p×1的矢量，a(θ,γ)是天线阵在方向θ和极化γ下的导向矢量。

a(θ,γ)=[a1(θ,γ)e-jω0τ1(θ),…,ap(θ,γ)e-jω0τp(θ)]T

其中ak(θ,γ)是第k号阵元在方向θ和极化γ上的幅度响应，τk(θ)是入射方向为θ的波前从参考点到第k号阵元的传播延时。

假设接收数据矩阵x(t)在时刻t1,…,tM处进行采样，则采样序列为x(t1),…,x(tM)。用γ1和γ2表示信号两个不同的极化状态(比如垂直极化和水平极化)。用a1(θ)和a2(θ)分别表示方向θ上γ1和γ2两种极化状态的导向矢量。

a1(θ)=a(θ,γ1)

a2(θ)=a(θ,γ2)

(5)

考虑第i个信号的导向矢量a(θi,γi)。该矢量可以用导向矢量a1(θi)和a2(θi)的线性组合来表示。

a(θi,γi)=A(θi)ki

(6)

其中A(θi)为2p×2矩阵

A(θi)=[a1(θi),a2(θi)]

(7)

ki为2×1复矢量

ki=[ki1,ki2]T

(8)

(9)

定义K为极化对角矩阵

K=diag[k1,…,kq]

(10)

更进一步，X和N为2p×M的采样数据矩阵，S为q×M的矩阵，则接受数据向量可以写为

(11)

其中

(12)

最大似然估计器为

(13)

其中

(14)

tr[]是括号中矩阵的迹，R是数据协方差矩阵

3 实验验证分析

1)对极化参量不变的多径相关信号进行仿真分析。信号频率为12.386MHz，第一径入射方位角为95°、俯仰角为20°，极化轴比为0.8、相差为80°，第二径入射方位角为98°、俯仰角为10°，极化轴比为0.6、相差为120°，两径相关系数为0.8。采用基于24阵元极化敏感均匀圆阵的侦测合一阵列，对本文提出的极化似然测向方法与传统空间谱测向方法的测向性能进行了对比分析，对比结果如图2所示。

从测试结果可以看出，本文提出的极化似然测向方法能够解决侦测合一阵列的极化敏感问题以及短波的多径信号测向问题。

2)利用某侦测合一阵地对不同信号类型、不同强度、不同距离、重点低频段的天波信号进行了现场测试分析。侦测合一阵列采用24阵元水平对数周期极化敏感均匀圆阵，信号类型为HFDL，频率为3.728MHz，来波方位138°，距离2563km，信噪比8dB，反射层有E层、F层，模式有E模式、F2层低角模式；信号类型为3G-ALE，信号频率为7.577MHz，来波方位135°，距离3520km，信噪比7dB，反射层有Es层、F层，模式有Es模式、F2层低角模式、F层两跳模式。基于同一个侦测合一阵地实际采集的相同天波数据，对本文方法与传统空间谱方法的测向性能进行了对比分析，对比结果如图3、图4所示。

图3 信号频率3.728MHz

图4 信号频率7.577MHz

从实际测试结果可以看出，本文提出的极化似然测向方法适用于天波信号，特别对低频段弱信号具有很好的测向性能，相对于传统空间谱方法，能够适应短波天波信号的多径及极化旋转。

4 结束语

针对传统空间谱测向方法不能适应短波天波信号的多径及极化旋转等问题，提出了一种适用于极化敏感侦测合一阵列的测向新方法。通过将接收信号的极化向量分解为两个互相正交的极化向量，可拟合任意极化状态的天线响应，从而得到天线阵在极化域的全部响应，可同时实现对信号的方位角、仰角、轴比和初相差的联合估计，同时利用似然估计方法可解决短波多径相关信号的测向问题，从实验验证结果可以看出，本文所提方法对实际天波信号具有较好的测向性能。本文的研究成果已可应用于某侦测合一系统，可满足实战需求。