非均匀共形天线阵多基线联合测角及最优布阵设计

殷 飞 吴一龙 吴 迪

(西安电子工程研究所 西安 710100)

0 引言

非接触性攻击成为了现代战争的重要作战方式，精确打击能力将主导作战进程。精确打击能力很大程度上是以侦察和识别能力为条件的，在精确制导武器系统中各类体制的雷达起着十分重要的作用。作为雷达对抗的主要技术手段之一，反辐射导弹是一种先进的硬杀伤武器，可对敌有效实施防空压制、反舰、空中打击，已成为各国优先发展的信息战进攻武器[1-4]。因此，大力发展反辐射导弹对于夺取制空权、制海权，继而真正达到制信息权是至关重要的。

传统的单模反辐射导弹易受雷达关机、诱饵等问题的困扰，无法有效完成防空压制任务。主被动复合反辐射导弹通过融合主被动雷达探测到的信息能有效实现抗雷达关机和抗诱饵[5-6]。由于主被动复合反辐射导弹口径有限，被动雷达天线需要采用共形设计，以给主动雷达留出足够空间，确保其探测性能。而基于被动共形天线阵的方位俯仰二维测角是主被动复合反辐射制导技术中的难点。

已有的被动共形天线阵都是采用简单的均匀共形布阵设计，为实现性能指标，典型配置通常需要8个天线单元，相应需要8个接收通道和较高信号处理硬件要求，不能满足军方最新提出的反辐射导弹主被动复合雷达导引头小型化、低成本和低功耗的要求。

常用的均匀共形布阵方式对被动两维测角来说并非是最优布阵方式，布局合理的非均匀布阵方式能更大程度地利用被动天线单元的测角效能，具备在更少的天线单元数量的条件下达到和简单均匀共形布阵相当的测角能力的潜力。更少的天线单元对应更少的接收通道个数，更少的AD采样路数，并能降低对信号处理硬件的要求，实现小型化、低成本和低功耗的目标。

针对非均匀布阵情况，本文首先将只能完成一维测角的传统干涉仪推广为能完成方位俯仰二维测角的双基线联合干涉仪；其次，提出了多基线联合解模糊算法以解决测角模糊问题；最后，提出了一种非均匀最优布阵评价准则和最优布阵选择方法，通过基于超算并行平台的仿真实验验证了所提方法的有效性。

本文第1节对典型宽带共形天线阵被动探测系统做了简述。第2节详述了所提出的非均匀共形天线多基线联合测角方法。第3节提出了非均匀最优共形布阵设计方法和并行计算实现方法。第4节给出了实验结果及分析。最后，对本文研究内容进行了总结。

1 典型宽带共形天线阵被动探测系统简述

典型宽带共形天线阵被动探测系统工作频率范围为2～18GHz，整个被动接收天线系统主要包含共形超宽带辐射阵面、射频前端模块、超宽带数字接收机以及框架结构等部分，其系统组成框图如图1所示。

图1 典型共形超宽带天线系统组成框图

典型天线阵面由8个辐射单元等间隔均匀分布于弹体表面，如图2所示。宽带天线阵在接收状态工作时，8个单元可分别接收来自空间的信号，随后将接收到的各路单元信号分别输出至8个独立的接收通道，各接收通道再分别经过下变频与AD采样后送入数字信号处理器，最终在数字域中进行方位俯仰二维测角。

图2 典型宽带共形天线阵面分布示意图

2 非均匀共形天线阵多基线联合测角

第1节介绍的典型宽带共形天线阵被动探测系统采用被动天线均匀布阵的方式，这种共形布阵方式对被动两维测角来说并非是最优布阵方式，布局合理的非均匀布阵方式能更大程度地利用被动天线单元的测角效能，具备在更少的天线单元数量的条件下达到和均匀共形布阵相当的测角能力的潜力，并有助于实现小型化、低成本和低功耗的目标。

本节针对非均匀共形天线布阵的情况，开展方位俯仰二维测角方法研究。首先将传统干涉仪推广为双基线联合干涉仪，以实现方位俯仰二维测角；其次，提出多基线联合解模糊方法完成二维测角解模糊。

2.1 双基线联合干涉仪

传统干涉仪能够测量低仰角情况下辐射源的方位角，但在反辐射导弹导引头、卫星电子侦察等应用中，需要同时测量辐射源在水平面内的方位角和垂直面内的俯仰角。传统干涉仪无法完成辐射源方位俯仰二维测角，本节将传统干涉仪推广为双基线联合干涉仪，使其能够完成对辐射源的方位俯仰二维测角。

双基线联合干涉仪由两个处于不同方向上的两个传统单基线干涉仪组成。双基线联合干涉仪的一个基本模型如图3所示，双基线联合干涉仪由OA方向和OB方向上的两个单基线干涉仪组成，基线OA和OB相互垂直，设其基线长度分别是lA和lB。图中xoy面表示水平面，z轴垂直于xoy面，设S是辐射源入射方向上某点。首先，沿S分别做垂直于xoy面和xoz面的垂线SP和SQ。然后分别沿P和Q做垂直与基线OA和OB的线段PR和QT。因此，∠SPO,∠SQO,∠ORP和∠OTQ都是直角。此外，由三垂线定理可知∠ORS和∠OTS也是直角。

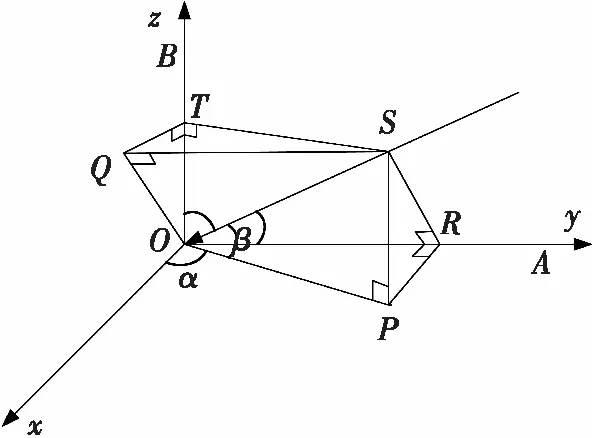
图3 双基线联合干涉仪原理图

设来波的方位角和俯仰角分别为α和β，来波方向与基线OA和OB的夹角分别为θa和θb。来波在基线OA上的相位差为φa，在基线OB上的相位差为φb。基于单基线干涉仪原理可得

(1)

(2)

从图3中的几何关系可得

(3)

(4)

将式(3)和式(4)分别代入式(1)和式(2)可得

(5)

(6)

因此，在鉴相器得到两条基线上的相位差φa和φb后，通过求解上述二元方程即可得到来波方位角α和俯仰角β，由此便可完成方位俯仰二维测角。

2.2 多基线联合解模糊

从基本干涉仪原理可知，在基线长度一定的情况下，如辐射源频率较高便会出现测角模糊，即通过干涉仪测角会得到几个可能的测角结果。已有文献提出过多种解模糊算法[7-9]，但都有特殊条件限制，不适用于被动非均匀共形天线阵二维测角解模糊。因此，本节提出一种新的多基线联合的方法来完成非均匀共形天线阵二维测角解模糊。

一个5单元非均匀共形天线阵如图4所示，每一对基线可以按照2.1节的方法求得一个二维模糊角集合。设有n对基线，则可得n个模糊角集合S1,S2,…,Sn。

图4 多基线联合解模糊示意图

定义点s与点集Si的距离为式(7)。

(7)

其中，Sij表示点集Si的第j个元素，|Si|表示Si中的元素个数，‖·‖2表示欧几里得范数。

那么无模糊的方位俯仰角s*就是距所有模糊角集合最近的那个点，可以通过式(8)求出。

(8)

多基线联合解模糊算法如表1所示。

表1 多基线联合解模糊算法

3 非均匀最优共形布阵设计与实现

3.1 非均匀最优共形布阵设计

第2节针对非均匀共形天线阵，提出了多基线联合测角及解模糊方法。本节基于第2节提出的多基线联合测角方法，提出一种非均匀共形天线阵最优布阵设计方法，以达到在设定的天线单元个数下实现最高测角精度。

首先提出如下的布阵性能评价准则为

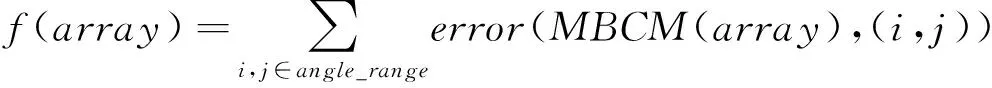
其中，array表示某种天线布阵方式，MBCM(array)表示在该天线布阵下的多基线联合测角方法(Multi-Baseline Combination Method) ，angle_range表示被动雷达瞬时测角范围，error(A,B)表示测角方法A在角度方向B上的测角误差。布阵性能评价函数f(array)刻画了天线布阵方式array在被动雷达瞬时测角范围内的总测角误差。

因此，本文提出如下的优化问题来求解最优的天线布阵为

上述优化问题能够找出能使总测角误差最小的天线布阵形式array*。非均匀最优共形布阵设计算法如表2所示。

表2 非均匀最优共形布阵设计算法

3.2 非均匀最优共形布阵设计算法并行实现方法

由于第3.1节提出的非均匀最优共形布阵设计算法计算复杂度很高，单核串行计算效率低，做一次布阵优化计算时间过长，本文通过对所提算法进行并行化实现，以在有效时间内得到最优布阵设计。

本文提出的并行布阵优化架构如图5所示。首先，将最优共形布阵优化问题进行可并行任务划分，结合可使用的并行节点数量，本文将原问题划分为75个可并行处理的子问题，分配给75个处理节点进行并行优化计算。利用第76个处理节点对前75个节点的优化结果进行收集整合，并综合计算出非均匀最优共形布阵问题的最优解，作为最优布阵输出。

图5 非均匀最优共形布阵设计算法并行化实现方法

4 实验结果及分析

为验证非均匀共形天线阵多基线联合测角及最优布阵设计方法的性能，开展了仿真试验验证。针对160mm口径寻找最优5单元非均匀共形天线阵问题，仿真试验采用超级计算机提供的并行计算平台，其中75个计算节点用来并行进行布阵设计子问题优化计算，第76个节点用来进行结果收集整理和最优布阵计算输出。

仿真得到的5单元最优非均匀共形天线布阵结果如图6所示。

图6 5单元非均匀共形天线最优布阵

基于该最优布阵，使用本文提出的非均匀共形天线阵多基线联合测角算法分别计算了对2GHz、4GHz、6GHz、8GHz、10GHz、12GHz、14GHz、16GHz、18GHz等典型频点目标的测角范围和测角精度，结果如表3所示。

表3 5单元非均匀共形天线最优布阵下各典型频点上的测角范围和测角精度

从试验结果可以看出：

1)非均匀共形天线阵多基线联合测角方法随着辐射源频率增加，测角精度提高，与基线波长比越大测角精度越高的基本原理一致。

2)所提算法在2～18GHz全频段范围内的测角范围能够覆盖方位/俯仰±20°。

3)5单元最优非均匀共形天线布阵在2GHz～4GHz频段的测角精度优于1.5°，在4GHz～10GHz频段的测角精度优于1°，在10GHz～18GHz频段的测角精度优于0.5°，该测角精度水平能够满足典型使用要求。

5 结束语

针对主被动复合反辐射制导中的被动非均匀共形天线阵方位俯仰二维测角问题，本文首先将只能完成一维测角的传统干涉仪推广为能完成方位俯仰二维测角的双基线联合干涉仪；其次，提出了多基线联合解模糊算法以解决测角模糊问题；最后，提出了一种非均匀最优布阵设计算法和该算法的并行实现方法。通过基于超算提供的并行计算平台的仿真实验验证了所提方法的可行性和有效性，为反辐射制导装备研制中实现更少的天线单元、更少的接收通道、更少的AD采样路数、可降低对信号处理硬件的要求，实现小型化、低成本和低功耗的目标奠定了基础。