基于ABAQUS二次开发对某机载吊舱的损伤容限分析
杨一帆 邰炜华 张敏强 李 智 苏力争
(西安电子工程研究所 西安 710100)
0 引言
损伤容限设计理论是一种以断裂力学为基础的设计理论,常用于飞机的整机设计与机载设备设计。由于机载设备在使用过程中,会受到因飞机的各种机动动作而产生的重复载荷作用,使得机载设备的某些关键承力部位承载能力下降,易产生疲劳损伤与疲劳断裂[1-4]。目前结构的损伤容限分析方法主要有实验法、工程公式法与有限元法。由于有限元法具有高效性与易编程性等特点,使得有限元法在解决结构损伤容限问题上得到了广泛应用[5-8]。
1 损伤容限基本理论
损伤容限理论是为了确立结构剩余强度,裂纹扩展速率与设备检修周期三者关系而存在一种结构设计理论。由于结构件在加工,运输,使用过程中会产生不易发现的缺陷与损伤,这些缺陷与损伤会随着载荷的作用而逐渐加重,致使结构件产生破坏,影响其使用的安全性与可靠性。结合断裂力学[9]理论知识,可以有效地解决大多工程实际问题,为结构设计的安全性提供了一种可以定量评估的方法。
损伤容限设计的主要目的是通过恰当的材料选择与合理的结构布局来保证结构件在检修周期内不会发生断裂与破坏,使设备的使用可靠性得到提升。由于机载设备的特殊工作环境,使得损伤容限设计理论在机载设备的结构设计中具有重要意义。
2 基于Python语言对ABAQUS的二次开发
2.1 二次开发程序基本结构
运用Python语言对ABAQUS软件进行二次开发,使ABAQUS软件可以对模型的损伤容限进行自动分析,输出各裂纹长度下的应力强度因子幅度ΔK。基于Python语言对ABAQUS软件二次开发的程序流程图如图1所示。

图1 ABAQUS二次开发程序分析流程
ABAQUS软件的二次开发程序可以自动完成对结构件的建模,装配,施加载荷,建立相互作用,创建网格等有限元计算的前处理。通过一个循环语句对裂纹进行自动设置,提高了有限元计算的效率,减少了人为重复修改裂纹数据的时间。
2.2 不同算例的损伤容限分析
2.2.1 断裂条件与材料选择
如图2所示,裂纹的主要形式有三种,本文主要对I形裂纹进行分析与计算。如图3所示,疲劳裂纹扩展主要分为三个阶段,裂纹初始萌生阶段,裂纹稳定扩展阶段,裂纹快速扩展阶段,损伤容限理论所研究的是裂纹的稳定扩展阶段。

图2 裂纹类型

图3 疲劳裂纹扩展阶段
为了使疲劳裂纹开始扩展,应力强度因子幅度ΔK应满足
ΔK>ΔKth
(1)

疲劳裂纹瞬间断裂,应力强度因子最大值KImax应满足
KImax≥KIc
(2)

算例的材料选取2A12铝合金,材料参数如表1所示。

表1 材料参数
2.2.2 算例的结构尺寸
运用三维绘图软件UG对三种不同尺寸的算例进行建模,具体尺寸如图4所示。

图4 不同算例结构尺寸
图4中a为初始预制半裂纹长度,单位为mm。
2.2.3 基于程序对不同算例的损伤容限分析
通过运行程序,实现对算例的自动分析,在计算中,取循环载荷应力比R为0.06,最大载荷σmax为3500N/Wt,式中t为算例厚度,单位为mm;W为算例宽度,单位为mm。初始半裂纹长度α为2mm。
(3)
式(3)中σmin为循环载荷的最小载荷单位为Mpa,σmax为循环载荷的最大载荷,单位为Mpa。
部分计算云图如图5至图7所示。



如应力云图所示,裂纹尖端形成塑性区,且随着裂纹的扩展,裂纹尖端的应力集中现象逐渐增强。通过程序计算得到应力强度因子幅度ΔKI随半裂纹长度α的变化曲线如下所示:
如图8所示,随着裂纹的扩展,应力强度因子幅度ΔKI逐渐增大,并最终达到断裂条件,致使算例瞬间断裂破坏。

图8 ΔKI变化趋势图(程序计算)
Paris公式为
(4)
式(4)中C,n为材料常数,Paris公式是用于描述恒幅载荷作用下的疲劳裂纹扩展速率。将Paris公式积分可以得到式(5)。
(5)
式(5)中△σ为载荷幅度,单位为Mpa,△α为裂纹扩展长度,单位为m;α0为初始裂纹长度,单位为m;J为裂纹穿透因子。通过式(5)可以得到三种算例基于程序计算结果的疲劳裂纹扩展寿命曲线。
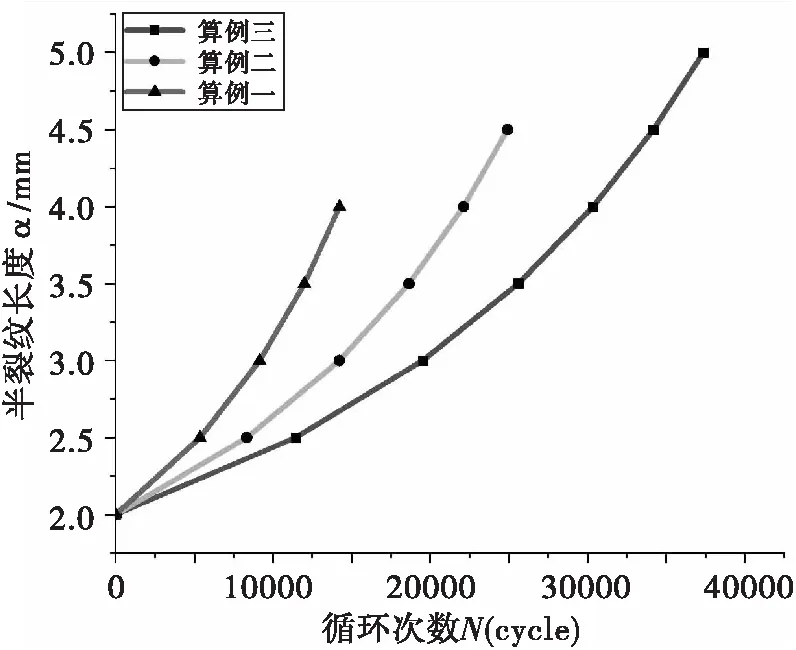
图9 不同算例α-N曲线图(程序计算)
2.2.4 工程算法对不同算例的损伤容限分析
通过查询损伤容限手册[10]可以得到中心穿透裂纹板应力强度因子KI的计算公式为
(6)
最大应力强度因子为
(7)
应力强度因子幅度为
(8)
Δσ=σmax-σmin
(9)
其中σ为中心裂纹板所受均布载荷,单位为Mpa;J1为裂纹穿透因子;α为中心半裂纹长度,单位为mm;σmax为循环载荷最大值,σmin为循环载荷最小值,单位为Mpa;R为循环载荷应力比;Δσ为载荷幅度,单位为Mpa。

图10 中心穿透裂纹板示意

图11 穿透因子变化曲线
计算条件与程序计算时一致,通过工程算法得到应力强度因子幅度ΔKI随半裂纹长度α的变化曲线如图12所示。

图12 ΔKI变化趋势图(工程计算)
同样通过式(5)可以得到三种算例基于工程计算结果的疲劳裂纹扩展寿命曲线如图13所示。

图13 不同算例α-N曲线图(工程计算)
2.2.5 数据对比与分析
为了验证ABAQUS二次开发程序的准确性与可靠性,本节将对三个不同尺寸算例的损伤容限分析数据进行对比。
首先对两种方式计算得到的应力强度因子幅度ΔKI进行对比。如图(14)所示,算例一ΔKI的平均相对误差为10.68%;算例二ΔKI的平均相对误差为5.03%;算例三ΔKI的平均相对误差为3.28%,相对误差均小于15%,满足工程需求。

(a)算例一
对两种方式计算得到的疲劳裂纹扩展寿命曲线α-N曲线进行对比;如图15所示,所有α-N曲线的趋势基本相同,随着裂纹的扩展,裂纹扩展速率逐渐增大。算例一α-N曲线的平均相对误差为6.03%;算例二α-N曲线的平均相对误差为1.12%;算例三α-N曲线的平均相对误差为4.03%,相对误差均小于15%,满足工程需求。本节旨在验证ABAQUS软件二次开发程序,为后续分析计算打下基础。
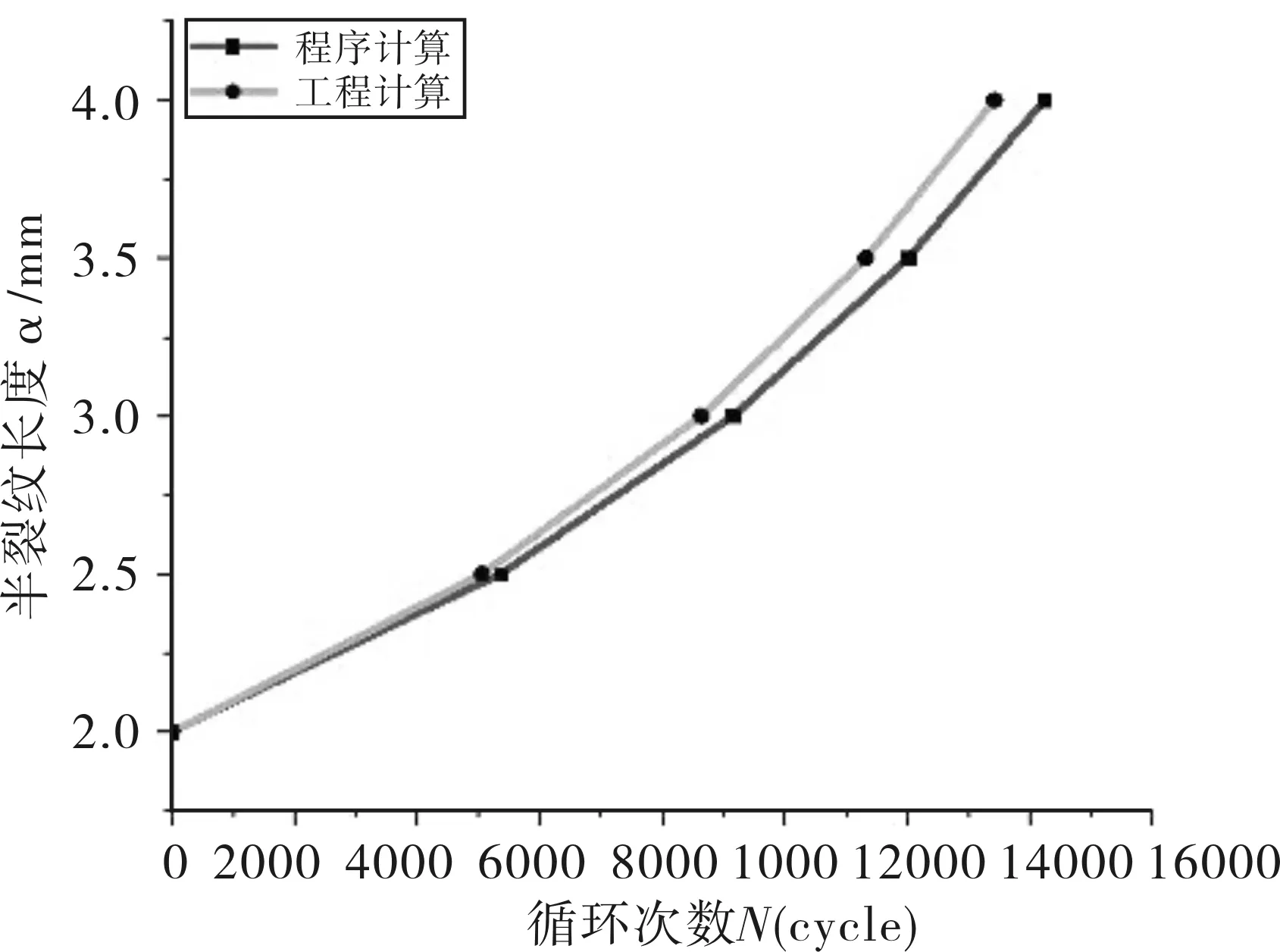
(a)算例一
3 某机载吊舱的损伤容限分析
3.1 某机载吊舱的结构与试验条件
如图16所示,某机载吊舱通过两个吊耳与总站连接,主要承力部位为吊耳部位,吊耳材料为2A12铝合金。按照研制要求,该机载吊舱需能够承载峰值为20g的重复冲击载荷(三轴六向),冲击波型为后峰锯齿波,单次冲击持续时间为11ms,吊舱总重为50kg。通过对吊耳结构的分析计算可以得到:吊耳对垂直向下方向的冲击最为敏感,即垂直向下的冲击对吊耳的威胁最大。

图16 机载吊舱结构示意

图17 冲击载荷波形图
运用有限元软件ABAQUS对吊舱进行静力分析,得到吊耳的危险位置如图18所示。
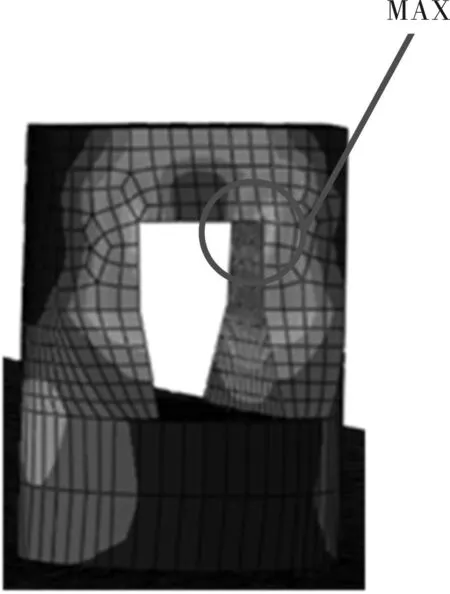
图18 危险位置示意
3.2 计算结果分析与寿命预测
为了简化计算,提高运算效率,将吊耳模型进行简化处理。机载设备的疲劳破坏,是多种因素共同作用造成的,如结构加工缺陷,腐蚀,结构过载,维护不当等,固对吊耳两侧的危险部位预制裂纹,预制半裂纹长度为α,单位为mm,如图19所示。
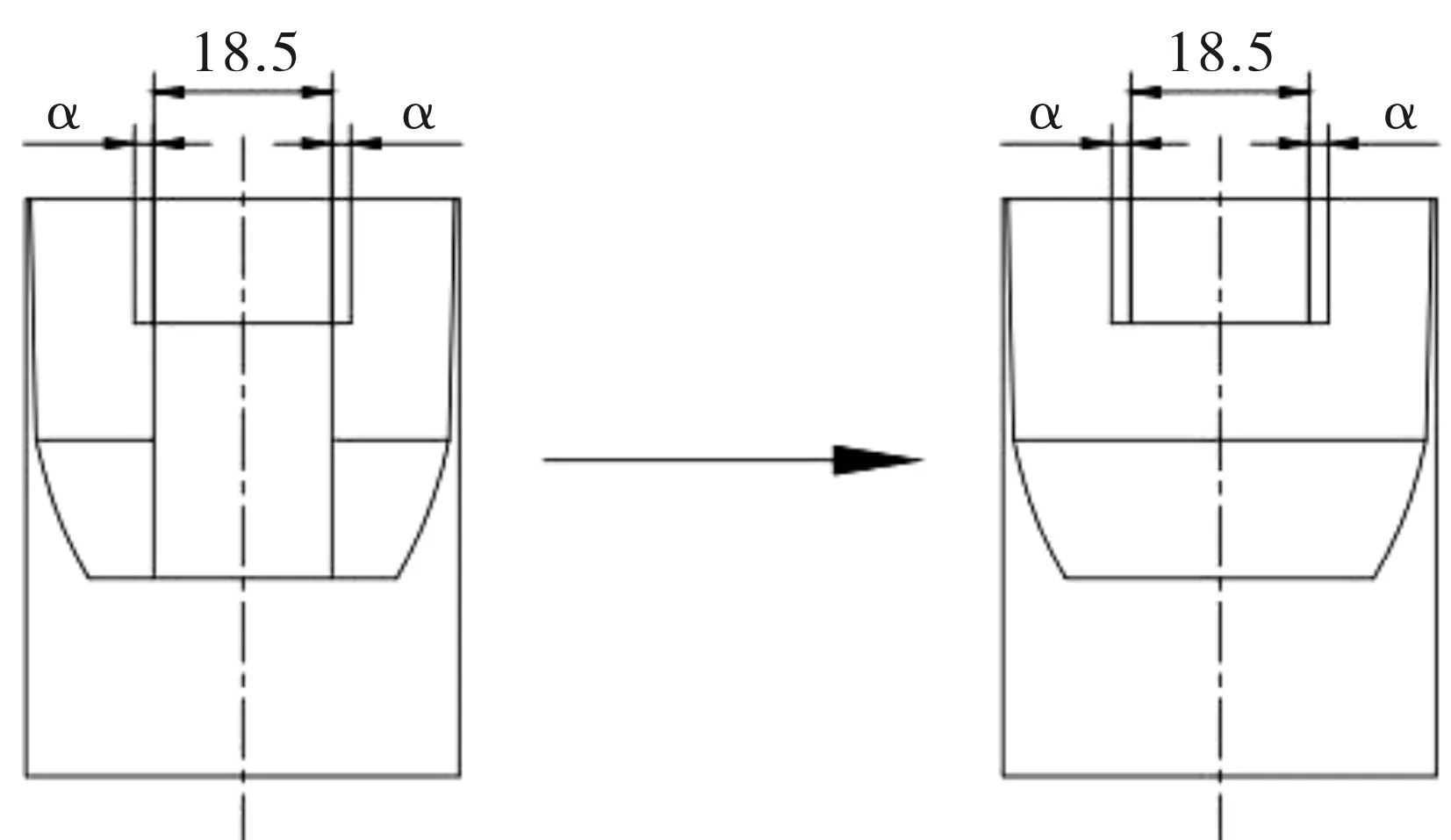
图19 吊耳简化模型
通过编写程序,使吊耳在自动建模时,网格选择C3D8R减缩积分六面体网格,并对吊耳结构进行拆分,以提高网格质量,提升计算准确性,应力比R取0.06。结构拆分及网格划分如图20所示。

图20 拆分及网格划分
通过程序计算得到的应力强度因子幅度△K与半裂纹长度α的关系如图21所示。

图21 吊耳ΔKI变化趋势图

部分裂纹长度下的应力云图如图22所示:

将不同裂纹长度αi+1=αi+Δα带入式(5)可以推算出吊耳在冲击载荷作用下的疲劳寿命曲线,如图23所示。

图23 吊耳疲劳裂纹扩展曲线
从图23可以看出,随着疲劳裂纹的增长,疲劳裂纹扩展速率也在增大。机载吊舱吊耳在初始半裂纹长度α=0.7mm的条件下,疲劳裂纹扩展寿命为1.15×106。由此可以得出,结构在该循环冲击载荷作用下的剩余强度较高,且裂纹开始扩展所需的初始裂纹长度较大,此初始裂纹在设备日常检修时通过观察比较容易发现。综上所述,该结构满足损伤容限设计要求与实际工程使用需求。
4 结束语
本文应用Python语言对ABAQUS软件进行二次开发,通过对不同结构算例的损伤容限分析,验证了二次开发程序计算的准确性与可靠性,各算例通过程序计算的结果与工程经验公式计算结果的相对误差均不超过15%,满足工程需求,并对各算例的疲劳寿命进行了预估。运用二次开发程序,对某机载吊舱危险部位进行损伤容限分析,通过程序输出数据分析某机载吊舱危险部位的开裂条件,并对结构的疲劳寿命进行了预估,为某机载吊舱关键承载部位检修周期的制定提供了理论依据,并从损伤容限分析的角度验证了某机载吊舱结构设计的安全性与可靠性。为结构的损伤容限设计提供了一种验证与计算的方法。

