基于动态自适应混沌粒子群优化算法的干线协调控制方法①

郭海锋 黄贤恒 徐 甲 乔洪帅

(*浙江工业大学信息工程学院 杭州310023)

(**银江股份智慧交通研究院 杭州310030)

0 引言

在城市路网中,主干道往往承受着大部分的交通负荷,如何协调主干道,使尽可能多的直行车辆不停顿地通过主干道,成为了改善城市交通拥挤问题的关键所在。

现有的干线绿波协调控制优化通常采用2 种设计思路[1]:最大绿波带宽和最小延误。国内外学者对这2 种设计思路已经做了大量研究。基于混合整数线性规划理论,文献[2,3]建立了经典的MAXBAND 模型,并在此基础上,扩展了MAXBAND 模型,构建了MAXBAND-86 模型。文献[4,5]提出了经典的MULTIBAND 模型,考虑了路段的需求,且不同路段带宽可以不同。文献[6,7]取消绿波带中心对称的约束,对传统的MULTIBAND 进行改进,得到的绿波带带宽更大,更充分地利用绿灯时间。文献[8]在现有的绿灯中心型双向绿波协调设计数解法的基础上,提出了绿灯终点型双向绿波协调设计数解法。文献[9]通过对上、下行车辆在交叉口的延误规律进行分析研究,建立了经典的延误三角形模型。文献[10]考虑车队离散,引入Robertson 模型,分析车辆的到达与驶离情况,建立了相位差优化模型,优化目标为系统总延误或者停车次数。文献[11]针对经典延误三角形的局限性,建立了平行四边形的延误模型。文献[12]考虑相邻交叉口排队溢出问题,将排队长度引入模型,采用遗传算法对信号配时参数优化。文献[13]基于相邻交叉口交通流到达特性,分析干线协调内在机理,并且将排队长度引入延误计算过程,建立了干线协调控制相位差模型。文献[14]通过对城市路网的分析,建立了基于自适应粒子群优化算法的城市交通信号区域最优控制模型。文献[15]分析路网交通流的动态特性,提出区域车辆延误模型,采用混沌遗传算法优化模型。

上述研究,无论是基于最大绿波带宽,还是基于最小延误建立相位差模型,均忽略了车辆在干线内部交叉口的运行特性,把车辆的到达率均匀化处理,没有考虑车辆转出、非协调相位车流对延误的影响,这并不符合实际情况。本文针对上述问题,提出基于上游交叉口信号配时参数的车辆到达率预测,把车辆转出比例和非协调相位车辆数引入模型,设计了一种动态自适应混沌粒子群优化算法(dynamic self-adaptive chaotic particle swarm optimization algorithm,DACPSOA)对模型进行求解。最后通过仿真实验与单点控制和数解法进行对比,验证本文算法的性能和优势。

1 双向绿波协调控制优化模型

如图1 所示,设某干线协调控制子区包括n个交叉口,协调的方向为由西向东和由东向西2 个方向,设由西向东为上行方向,由东向西为下行方向。为了简化建模过程,作如下假设。

图1 干线协调控制子区示意图

(1) 协调控制子区相邻交叉口之间的距离适中,距离在300 m 到800 m 之间,协调相位的放行方式为对称放行。

(2) 由上游交叉口非协调相位驶向下游交叉口的车流,在下游交叉口协调相位的红灯期间均匀到达。

(3) 采用Robertson 离散模型来描述上游交叉口协调相位的车流到达下游交叉口协调相位的过程,本文假设车流中每个时间段转出的车辆比例相同。

1.1 参数说明

假设干线协调控制系统由n个交叉口组成,交叉口之间的距离为ln-1,n,公共周期为C0,交叉口之间的相对相位差为On,n-1,交叉口相位j绿灯时长为gn,j。

公共周期C0的确定是根据Webster[16]理论确定每个交叉口的周期时长Cn,按照周期最大原则确定关键交叉口,并且选取关键交叉口的周期时长作为公共周期时长C0,即:

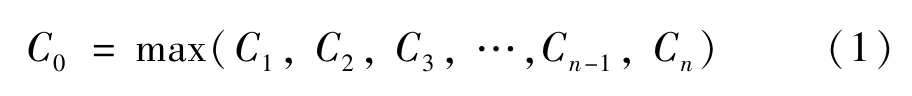
各个相位的绿灯时间分配原则[1]如下。

对于关键交叉口,按照饱和度相等[1]的原则为各个相位分配时间;对于非关键交叉口,按照不等饱和度[1]原则为各个相位分配时间,即计算各个非协调相位饱和度实用限值等于0.9 时所需的绿灯时间之和,将剩下的绿灯时间分配给协调相位。

通过对相位差的分析,2 个交叉口之间的相位差与公共周期C0满足On,n-1+On-1,n=C0,以上行方向为例,以边界交叉口1 的协调相位的开启点作为起始点,那么交叉口n的协调相位的开启时刻tCn为

如图1 所示,干线子区内各个交叉口协调相位车流量的来源是不同的。将干线子区内的交叉口划分为两类:一类是边界交叉口,协调相位的流量由外界输入;另一类是内部交叉口,协调相位的流量由内部交叉口输入。

1.2 基于上游交叉口信号配时参数的车辆到达率预测

边界交叉口不受上游交叉口的影响,可以假设车流到达是随机的。然而内部交叉口车流的到达不仅受到上游交叉口的信号配时参数影响,还与车队的离散、车辆的转出以及交叉口的信号配时有关。如何正确预测干线内部交叉口车辆的到达率,对于减少车辆延误、提高干线的通行效率具有重要意义。

1.2.1 边界交叉口协调相位车流的到达率与释放率

边界交叉口协调相位的车流量是由干线外部进入的,车流的到达受上游交叉口的影响较小,所以可以认为是随机到达的。如图1,以上行方向为例,交叉口1 协调相位车流的平均到达率为q1,j,所以边界交叉口1 协调相位车流的到达率与释放率为

交叉口1 协调相位在一个周期车辆的到达与释放过程如同2 所示。

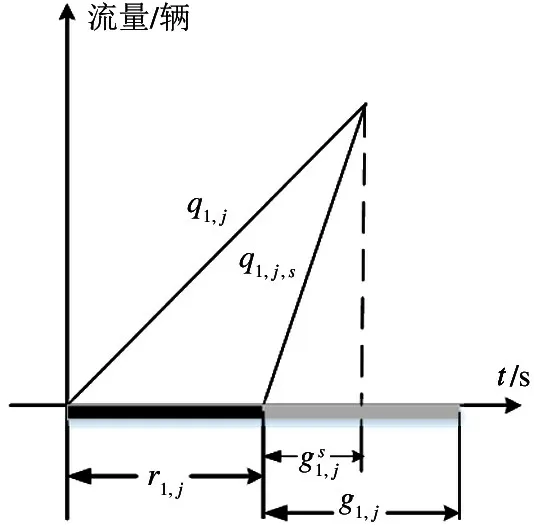
图2 交叉口1 协调相位车辆排队与消散

根据车辆到达与释放守恒的关系,计算出车流饱和释放的时间为

1.2.2 内部交叉口协调相位车流的到达率

以上行方向为例,内部交叉口包括2,3,4,…,n,对于内部交叉口来说,车流的到达并不是随机的。本文提出基于上游交叉口信号配时参数的车辆到达率的预测方法,建立车流到达率与上游交叉口释放率、路段长度、行驶速度、车队离散以及车辆转出的关系,依次预测车流到达内部交叉口的到达率。对于车队的离散,采用Robertson 离散模型进行离散化处理,本模型车流的离散时间段选取1 s,那么下游交叉口n车流的到达率与上游交叉口车流的释放率有如下的数学关系:

如图1 所示,下游交叉口n协调相位的车流由3 股车流组成。

(1)上游交叉口n-1 右转相位进入干线的车流,该股车流不受信号的控制,以恒定的到达率到达交叉口n-1,所以在每个周期到达下游交叉口n协调相位的车辆数为

式中,qn-1,j为交叉口n-1 右转相位j车流的到达率;为交叉口n-1 右转相位j车流到达交叉口n协调相位的比例。

(2)上游交叉口n-1 左转相位进入干线的车流,该部分车流以恒定的到达率到达交叉口n-1,所以在每个周期到达下游交叉口n协调相位的车辆数为

式中,qn-1,j为交叉口n -1 左转相位j车流的到达率;为交叉口n-1 左转相位j到达交叉口n协调相位的比例。

(3)上游交叉口n-1 协调相位进入干线的车流,该部分车流是交叉口n协调相位到达车流的主要组成部分,由式(6)对车流到达下游交叉口n的到达率预测。考虑车队的离散,到达下游交叉口n的到达率小于一个值q时,则是无车辆到达,所以必然存在一个阈值Kn,当时段大于Kn后则没有车辆到达,由式(6)可得时间点车辆到达下游交叉口n的车辆到达率为

由式(2)可知,上游交叉口n -1 的协调相位绿灯启亮时刻为tCn-1,此时车队头车越过停车线驶向下游交叉口n,在tn-1,n到达下游交叉口。所以车队头车到达下游交叉口n协调相位的时刻为

尾车到达下游交叉口n协调相位的时刻为

由式(9)、式(10)可知,下游交叉口n在红灯期间车流的到达率为

所以,内部交叉口n协调相位j车流的到达规律为

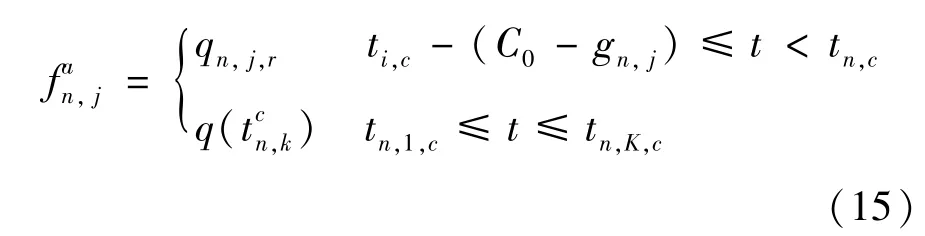
1.3 干线协调相位延误的计算

以上行方向为例,协调相位的延误分为边界交叉口的延误与内部交叉口的延误,但是边界交叉口的延误与相位差无关,本文重点分析内部交叉口协调相位的延误。内部交叉口协调相位的延误可以分为两部分,一部分是上游交叉口非协调相位(左转、右转)驶来的车流产生的延误Dn,1,另一部分是上游交叉口协调相位释放的车流产生的延误Dn,2。

1.3.1 上游交叉口非协调相位车流延误

该部分车辆在下游交叉口红灯期间均匀到达,所以车辆的延误等于红灯期间的延误加上绿灯启亮后车队消散产生的延误,如图3 所示,总的延误等于灰色梯形部分的面积,即:

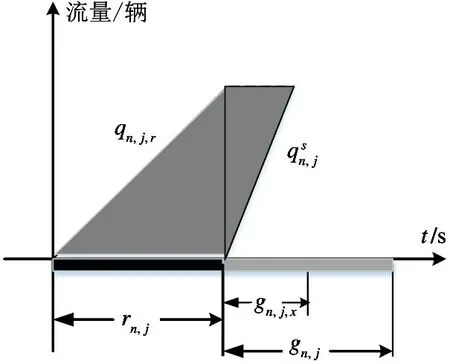
图3 非协调相位车流在交叉口n 延误示意图

另外,被红灯阻滞的车辆数为

排队车辆的消散时间为

1.3.2 上游交叉口协调相位车流延误

该部分是上游交叉口协调相位释放到达下游交叉口协调相位的车辆,产生的延误不仅和下游交叉口与上游交叉口之间的相位差有关,还与车队的头车、尾车到达下游交叉口的时间、下游交叉口协调相位的起始时刻、结束时刻以及非协调相位(左转、右转)车流释放结束时间有关,根据它们之间的关系,可以将延误的情况分为6 类进行讨论。

即从上游交叉口n-1 协调相位驶来的车队头车和尾车都在下游交叉口n协调相位绿灯期间到达,且头车到达时,前方没有排队车辆或者排队的车辆已经消散完全,此时该部分车流可以在交叉口n协调相位没有延误地通过,即:

那么交叉口n协调相位绿灯期间车流的释放规律如下:

即从上游交叉口n-1 协调相位驶来的车队头车在下游交叉口n协调相位绿灯期间到达,且头车到达时前方没有排队车辆或者车辆已经消散完全,但是车队的尾车到达时刻晚于绿灯结束时刻,所以此时被红灯阻滞的车辆数为

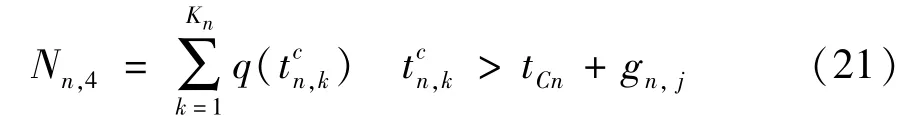
如图4 所示,受阻车辆的延误为灰色部分的面积加上黑色三角形的面积,所以受阻车辆的延误为

图4 车队尾部受阻延误分析图

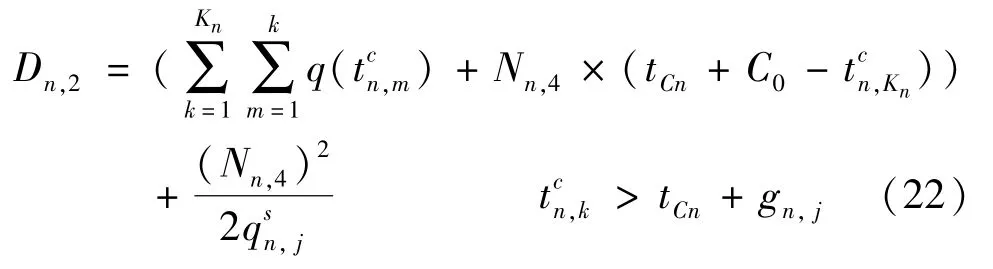
其中,第一部分是车队尾部信号灯变为红灯后等待产生的延误(灰色部分面积),第二部分是信号灯变为绿灯后车辆消散期间的延误(黑色三角形面积)。

那么在交叉口n协调相位绿灯期间车流的释放规律为

即从上游交叉口n-1 协调相位驶来的车队头车和尾车都在下游交叉口n协调相位绿灯期间到达,但是头车到达时,前方的排队车辆没有消散完全,所以此车流一部分会与前方排队车辆一起释放。设前方排队车辆消散使得该部分车流受到阻滞的时段为kp,由驶入与驶出的平衡可以得到kp为

所以在这种情况下,交叉口n协调相位绿灯启亮后以饱和流率释放的时间为

以车辆到达率q(t)释放的时间段为

本文假设非协调相位(左转、右转)进入干线的车辆较小,并且干线处在非饱和状态,所以从上游交叉口n-1 协调相位驶来的车辆在此种情况下可以在下游交叉口完全通过,即:

图5 车队头部受阻延误分析图

其中,第一部分是总延误(灰色部分面积)加上空白三角形的面积,第二部分是空白三角形的面积。

那么在交叉口n协调相位绿灯期间车流的释放规律为

即从上游交叉口n-1 驶来的车队头车在下游交叉口n协调相位绿灯期间到达,车队尾车到达时刻晚于绿灯的结束时刻,且头车到达时,前方的排队车辆还没有消散完全。由式(24)、式(25)得到车流受到阻滞的时段Kp和饱和流率释放的时间gn,j,x1,所以可以得到车队在红灯到达的时间段为

令k1=tCn+gn,j,x -,k2=kp -k1,k1是头车排队的时间段。k2是排队逐渐消散的时间段。如图6 所示,受阻车辆的延误等于灰色部分的面积加上黑色三角形的面积,所以受阻车辆的延误为

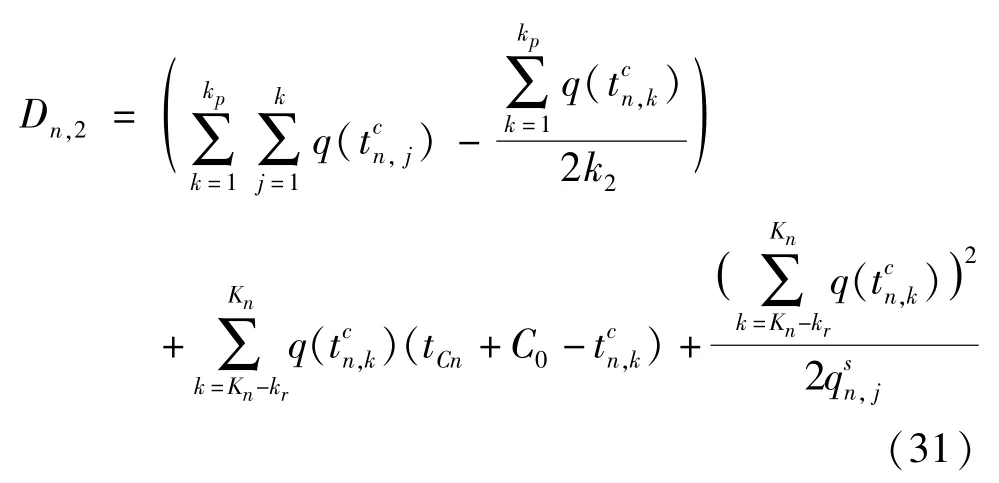
图6 车队受阻延误分析图

其中,第一部分是头车部分车辆受到前方排队车辆阻碍产生的延误(前面灰色部分面积),第二部分是尾车部分车辆在红灯期间等待的延误(后面灰色部分面积),第三部分是尾车部分车辆在下一绿灯启亮后车队消散的延误(黑色三角形面积)。

那么在交叉口n协调相位绿灯期间车流的释放规律为

即从上游交叉口n-1 驶来的车流在下游交叉口n协调相位红灯期间到达,车队尾部在绿灯期间到达,由式(24)、式(25)得到车流受到阻滞的时段kp和饱和流率释放的时间gn,j,x1。本文假设非协调相位(左转、右转)进入干线的车辆较小,并且干线处在非饱和状态,所以此种情况车流在交叉口n协调相位绿灯期间可以完全通过,即满足:

1)tCn+gn,j,x1≥,即车队在交叉口n以饱和流率驶出,如图7 所示,灰色部分的面积就是此种情况下车辆的延误,所以车辆的延误为

图7 车队受阻延误分析图

其中,第一部分和第二部分是图7 灰色部分的面积(总延误)和空白三角形面积之和,第三部分是空白三角形的面积。

那么在交叉口n协调相位绿灯期间车流的释放规律为

2)tn,c+gn,j,x1＜,即车队尾车在前方排队车辆消散之后到达的,令k1=tn,c +gn,j,x -,k2=kp -k1,如图5 所示,受阻车辆的延误为灰色部分的面积,所以受阻车辆的延误为

那么在交叉口n协调相位绿灯期间车流的释放规律为

即从上游交叉口n-1 协调相位驶来的车队头车与尾车均在下游交叉口n协调相位绿灯开启之前到达,所以车辆会在交叉口排队等待产生延误,干线处在非饱和状态,所以排队车辆在绿灯开启后会以饱和流率完全释放,饱和释放的时间为

如图8 所示车辆的延误等于灰色部分的面积,所以车辆的延误为

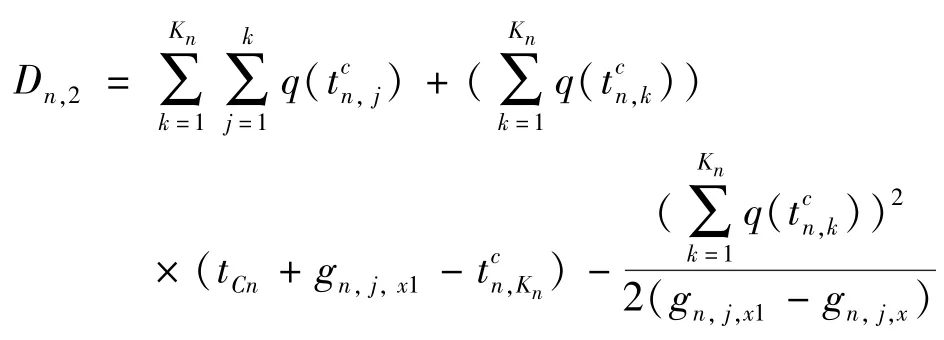
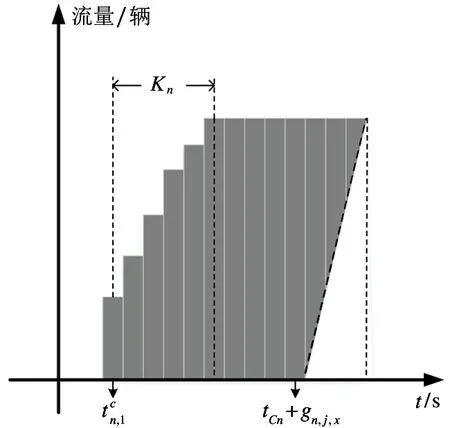
图8 车队受阻延误

其中,第一部分和第二部分是灰色图形的面积(总延误)加上空白三角形的面积,第三部分是空白三角形的面积。

那么在交叉口n协调相位绿灯期间车流的释放规律为

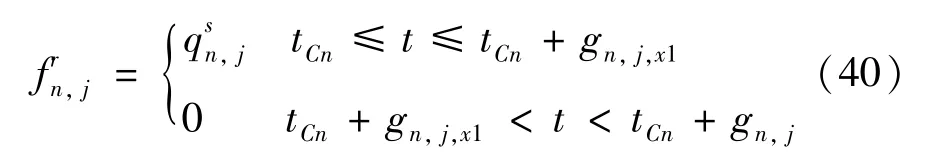
通过对这6 种情况的分析可知,交叉口n在上行方向的协调相位的延误等于Dn,1和Dn,2之和,下行方向协调相位的延误计算同上。

1.4 优化模型

通过对连续交叉口协调相位延误的分析,上游交叉口n -1 非协调相位(左转、右转)与协调相位释放的车流在路段上经过离散并且转出部分车流后,演化成了下游交叉口n协调相位的车流输入,在下游交叉口n的信号配时参数的作用下产生延误,以此类推,直到到达最后一个交叉口,上述演化的流程如图9 所示。

图9 协调控制作用下车流的输入输出关系

干线协调控制的目的是使得各个交叉口协调相位车流延误之和最小,即上行方向延误与下行方向延误之和最小,即:

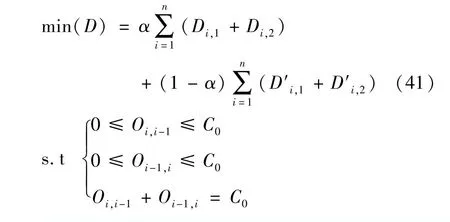
由于目标函数D是一个分段函数,且与优化的相位差之间是非线性的关系,所以,上述模型的求解可以看作是非线性规划问题,本文使用DACPSOA获得最优解。

2 DACPSOA

针对粒子群优化算法(particle swarm optimization algorithm,PSOA)存在局部最优、易陷入局部最小值并且收敛速度较慢的问题,本文提出了DACPSOA。

2.1 标准粒子群优化算法

PSOA[17]是从模拟社会行为而发展起来的具有全局寻优能力的优化工具。假设在D维空间中,有一个包含N个粒子的群体,粒子i的位置是xi=(xi1,xi2,…,xiD),i=1,2,…,N;粒子i的速度是vi=(vi1,vi2,…,viD);粒子i经历过的最好位置为pbesti=(pi1,pi2,…,piD),种群经历过的最好位置为gbest=(g1,g2,…,gD)。

粒子i在k次迭代后的第d维速度更新公式为

粒子i在k次迭代后的第d维位置更新公式为

其中w表示惯性权重,为非负数,用于调节解空间的搜索范围;c1、c2是加速度常数,用于调节学习最大步长;r1、r2是两个随机数,取值范围[0,1],用以增强搜索的随机性。

2.2 混沌优化策略

混沌是一种普遍的非线性现象,其行为复杂且随机,但其有精致的内在规律性。由于混沌的遍历性,利用混沌变量进行优化搜索会比盲目无序的随机搜索更具有优越性,它可以避免演化算法陷入局部最优的问题。所以将混沌引入粒子群[18],目的就是减少搜索的时间与范围,提高算法的搜索速度与搜索精度。粒子群混沌初始化的过程如下。

(1)根据搜索空间的维度,随机生成初始混沌向量。比如,在D维空间,混沌向量为y0=(y01,y02,…,y0D),y0D取值范围[0,1]。

(2)使用Logistic 方程如式(44)进行迭代产生混沌序列y1,y2,…,yQ,(Q ＞N),其中yi=(yi1,yi2,…,yiD);

式中μ为控制参量,这里取4。

(3)把产生的混沌变量yi通过式(45)逆映射到原解空间。

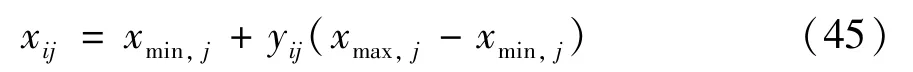
其中xmin,j、xmax,j分别代表变量的最大值与最小值。

(4)根据目标函数计算粒子的适应值,选取最优的N个粒子作为粒子群的初始粒子群。

2.3 动态自适应策略

在PSOA 中,惯性权重w通常是小于1 的,PSOA 在解决非线性规划问题寻找最优解时是非常复杂的,权重系数w不能反映实际的优化搜索过程。因此,本文提出了一种基于进化速度和聚集度来调整w的动态自适应惯性权重优化策略[19],惯性权重值随着进化速度因子和聚集度因子的变化而不断变化。

粒子群优化算法优化过程中进化速度因子为

式中,F(gbestk)代表当前迭代k的最优适应值,F(gbestk-1) 代表上一次迭代k -1 的最优适应值。粒子群优化算法优化过程中聚集度因子为

和自然界鸟类的觅食习惯一样,个体在搜索过程中,如果找到目标的可能性增加(即pspeed相对较大),那么它就不会加速到下一个位置,而是减速(减小惯性权重)飞向最优位置,所以当前搜索区域的搜索强度增加,以便于更快地找到最优位置;同时,为了增加算法跳出局部最优的能力,当某一代的适应值趋于稳定(即ptogether相对较大)时,应该增加粒子群的搜索空间(即增加惯性权重)。综上所述,惯性权重的动态自适应优化方程为

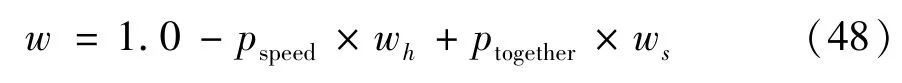
式中,wh的取值范围通常为0.4～0.6,ws的取值范围通常为0.05～0.20。

2.4 DACPSOA 的步骤

DACPSOA 从两方面改善了PSOA,引入混沌序列初始化粒子群和动态自适应改变惯性权重系数。DACPSOA 实施步骤如下。

步骤1粒子群初始化。设定种群规模m,搜索空间为D维,即协调交叉口的个数,根据搜索空间的维度,随机生成初始化混沌向量y0=(y01,y02,…,y0D),按照式(44)、式(45)初始化粒子群中的位置与速度。

步骤2根据适应度函数(目标函数)计算每个粒子的适应值。

步骤3对当前粒子适应度值大小与其历史最好位置pbest进行比较,若当前位置适应度值好于pbest,则将其作为历史最好位置。

步骤4对全局最好位置gbest 适应度值与当前粒子适应度值大小进行比较,若当前粒子适应度值好于gbest,则将其作为全局最好位置。

步骤5利用式(42)、式(43)对粒子位置和速度进行更新。

步骤6利用式(46)～式(48)对权重进行自适应调节。

步骤7计算粒子适应度值,更新pbest与gbest。

步骤8对算法终止条件进行判断,如果满足,则输出gbest 对应的解,算法结束;反之,返回步骤2,算法继续执行。

3 案例分析

3.1 仿真环境

为了验证本文建立的信号协调控制算法的有效性,仿真过程采用的是开源的交通仿真软件SUMO。

如图10 所示,仿真的路网结构是由3 个四相位的信号交叉口组成,相邻交叉口之间的距离分别为500 m、300 m 和650 m。启动损失时间为3 s、黄灯时间为3 s,直行车道和其他车道的饱和流率分别为1650 pcu/h 和1550 pcu/h。上行方向,交叉口1 到交叉口2 路段的平均速度为50 km/h,交叉口2 到交叉口3 路段的平均速度为43 km/h,交叉口3 到交叉口4 路段的平均速度为45 km/h;下行方向,交叉口4到交叉口3 路段的平均速度为50 km/h,交叉口3 到交叉口2 路段的平均速度为43 km/h,交叉口2 到交叉口1 路段的平均速度为47 km/h,仿真路网的各交叉口1 h 的流量见表1,车流转出比例见表2。

表1 交叉口流量数据/辆

表2 车流转出车辆的比例

图10 仿真路网结构

由表1 各个交叉口的流量数据,根据式(1)确定协调方案的公共周期为97 s,交叉口1 是关键交叉口;然后按照为交叉口各个相位分配绿灯时间,优化后的各个交叉口各个相位的绿灯时间如表3 所示。

3.2 模型求解

模型的求解与实施步骤如下:

(1) 建立相位差优化模型:通过对上游交叉口车流到达下游交叉口情况分析,建立双向绿波协调控制延误模型(其中α=0.5)。

(2)使用Python 编写DACPSOA,其中粒子群规模N=100,学习因子c1=c2=1,最大迭代次数为100,初始惯性权重wh=0.5,ws=0.1。

(3)运用DACPSOA 对双向绿波协调控制延误模型优化求解,求解步骤如2.4 节,得到交叉口之间的相对相位差。

(4)将得到的信号配时方案与相位差应用到交通控制系统中。

3.3 结果分析

模型求解得到的相位差分别为O2,1=27 s、O3,2=30 s、O4,3=59 s。为了与本文方案进行对比,采用单点控制和数解法进行方案仿真效果评价。其中根据数解法求解得到的相位差分别为O2,1=15 s、O3,2=48 s、O4,3=30 s。将各个交叉口信号配时参数和相位差输入到SUMO 仿真软件中,方案效果评价指标分别采取上行、下行和双向平均延误时间和平均停车次数,每隔5 min 进行数据的输出,仿真时长为1 h,仿真结果如图11 和图12 所示。

图11 和图12 分别为5 min 时间间隔3 种方案的平均延误和平均停车次数对比图。由图11 和图12可知,无论是平均延误还是平均停车次数,本文方法与数解法都相对于单点控制有所降低;与下行方向相比,上行方向的改善效果更加明显。与数解法相比,本文方法在上行方向平均延误与平均停车次数上均有所降低。下行方向平均延误与平均停车次数相差不多,说明本文在降低上行方向平均延误与平均停车次数的同时,并没有降低干线下行方向平均延误与平均停车次数。

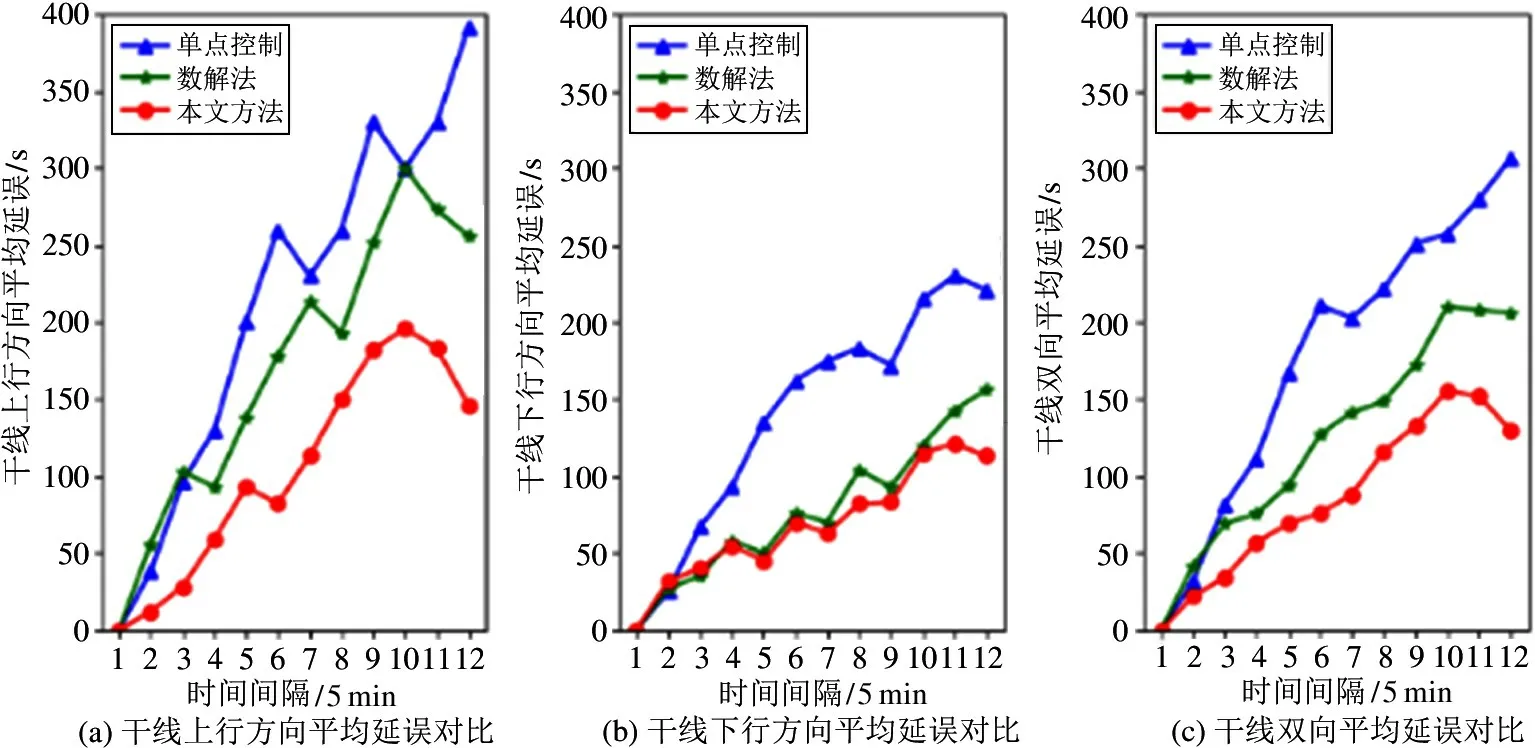
图11 干线平均延误对比

图12 干线平均停车次数对比

由表4 可知,与单点控制相比,本文方法对于干线双向平均延误、平均停车次数和平均行程时间的平均改善率分别为57.23%、64.01%和54.96%;与数解法相比,本文方法对于干线双向平均延误、平均停车次数和平均行程时间的平均改善率分别为24.97%、27.88%和22.20%。所以,就方案的平均收益而言,本文方法数值是最小的,优于单点控制与数解法。因此,本文方法能够有效地协调干线交叉口,降低车辆在干线上的平均延误、停车次数和行程时间,提高了通行效率。

表4 三种方案1 h 平均效益对比

4 结论

本文在分析干线车队运行特点的基础上,分析内部交叉口车辆的到达与释放规律,以整个干线延误最小为目标,优化交叉口之间的相位差。该方法根据外部车辆的到达率预测内部各个交叉口的到达率,对干线内部详细分析,更加符合真实的交通环境,能够优化干线的配时方案,提高交通干线的运行效率。针对标准的PSOA 容易陷入局部最优且收敛速度较慢的问题,本文结合混沌优化与动态自适应策略的特点,提出了DACPSOA,该算法有更好的稳定性和收敛速度。下一步工作将对干线车队离散模型进行分析以满足真实的交通环境。