基于Stokes矢量分析的偏光片光学参数测量
步海军,黎俊,夏燕,汤坤,王攀,曾婷婷,江铖,闵林
(1.苏州市计量测试院,江苏 苏州 215128;2.国家平板显示产业计量测试中心(苏州),江苏 苏州 215163)
0 引言
偏光片是平板显示器制造过程中的关键光学材料[1],在液晶显示器中,双层偏光片结构转换并解析偏振光,产生明暗对比,从而产生显示画面;在目前流行的AMOLED显示器中,偏光片的使用有效地降低了OLED显示器表面的反射,提升了显示器视觉效果。
偏光片透过轴和吸收轴的光谱透过率直接影响显示器的视觉效果,精确测量偏光片透过率对于显示器产品质量管控具有重要意义。偏光片透过率的传统测量方法为:通过一个已知偏振特性的偏振棱镜(或偏光片)产生具有特定偏振态的线偏光,考察其透过相对转动的待测偏光片后光强度的变化来计算偏振参数[2]。这种方法测量原理较为简单,所使用的测量仪器结构也不复杂,因此得到了广泛的应用。然而由于该方法中光源一般具有部分偏振特性,且探测器光响应存在偏振依赖性,导致其测量准确性不能满足先进制造的技术要求。而且,显示产业中所使用的偏光片一般是通过高分子薄膜材料拉伸后吸附碘分子制造的,在获得偏光特性的同时难免使得材料带有部分二向色性,即在相互垂直的光轴上存在位相差,该位相差对显示器的图像质量具有重要影响,需要对其进行详细表征,而传统测量方法无法表征该位相差。
针对上述问题,本文提出了基于Stokes矢量分析的方法,通过测量入射到样品以及从样品出射的偏振光的Stokes矢量,分析偏振态的变化,以此来解析偏光片的偏振光学参数。该方法不依赖于起偏器和检偏器的相对转动,可以有效避免光源和探测器的偏振特性引起的测量误差;而且,对于非理想偏光片,该方法可以同时测量出样品中可能带有的位相差。对该方法的基本原理、计算公式、装置组成进行详细介绍,并开展实际测量实验及不确定度分析,验证该方法的准确性与可靠性,为显示领域产品后续光学补偿设计提供重要指导。
1 测量原理及装置设计
光是一种电磁波,其电场分量可以表示为两个相互垂直的分量
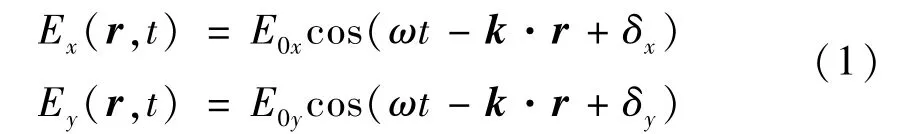
式中:E0x和E0y分别为x,y方向上电场分量的振幅;δx和δy分别为x,y方向上电场分量的初始位相;ω为圆频率;t为时间;k为波矢;r为空间坐标。
光也可以用Stokes矢量来表示[3],即

当光经过偏振元件后,光的偏振状态一般会发生变化,其Stokes分量变为

这一光与物质的相互作用过程可以用公式简单描述为

式中:M为偏振元件的4×4阶Mueller矩阵,其中各矩阵元包含了该元件的偏振光学参数信息,通过分析入射到偏振元件和从偏振元件出射的光的偏振状态的改变情况,即可解析得出偏振元件的光学参数。
对于理想偏光片,相互垂直的两个方向上只存在透过率的差异,而没有相位差,其Mueller矩阵可以写为
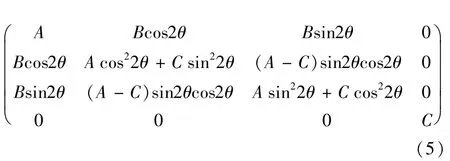

偏振光Stokes矢量的解析通过使光依次通过旋转的1/4波片和固定偏振棱镜实现。光的强度[4]可以表示为

式中:θ为1/4波片快轴相对于x轴的角度。测量得到入射光和出射光的Stokes矢量后就可以通过最优化算法来计算偏光片的参数[5]。
基于上述原理,本文设计的测量装置的光路如图1所示,其中S为光源,L与L‘为透镜,P与P‘为偏振棱镜,R与R‘为1/4波片,D为探测器。测量时,首先不将样品置入光路,测量入射光的Stokes矢量;再将样品置入光路,测量从样品出射的光的Stokes分量,此时的光路情况为:从光源S(在本文中为卤钨灯)出射的非偏振光经透镜L准直后进入偏振棱镜P和1/4波片R构成的圆偏振器形成近圆偏振光入射到样品(为了避免待测偏光片随机放置使入射偏振光偏振方向与偏光片吸收轴重合,导致出射光强度过低,影响透过率的测量精度,采用近圆偏振光作为测试光来测量透过率),之后从样品出射的光依次进入1/4波片R‘(R‘在步进电机的驱动下做旋转运动)和偏振棱镜P‘,在透镜L‘的作用下汇聚到探测器D(在本文中为光谱仪)。

图1 偏光片测量装置示意图Fig.1 Schematic diagram of the polarizer measurement device
2 测量结果及不确定度分析
显示器行业中使用的偏光片的一般结构如图2所示,其主要由PVA膜、TAC膜、保护膜、离型膜和压敏胶等复合制成,其中PVA膜是起偏振作用的核心膜材。

图2 常见偏光片结构Fig.2 Structure of common sheet polarizers
一般情况下,由于光路中光学元件表面的反射、折射、散射等效应,光源并非完全偏振光,偏振度Pol计算公式为

式中:Pol=1表示完全偏振光;Pol=0表示非偏振光;Pol介于0和1之间表示部分偏振光。本实验中光源的偏振度如图3所示,可以看出在可见光波段入射光具有非常高的偏振度。
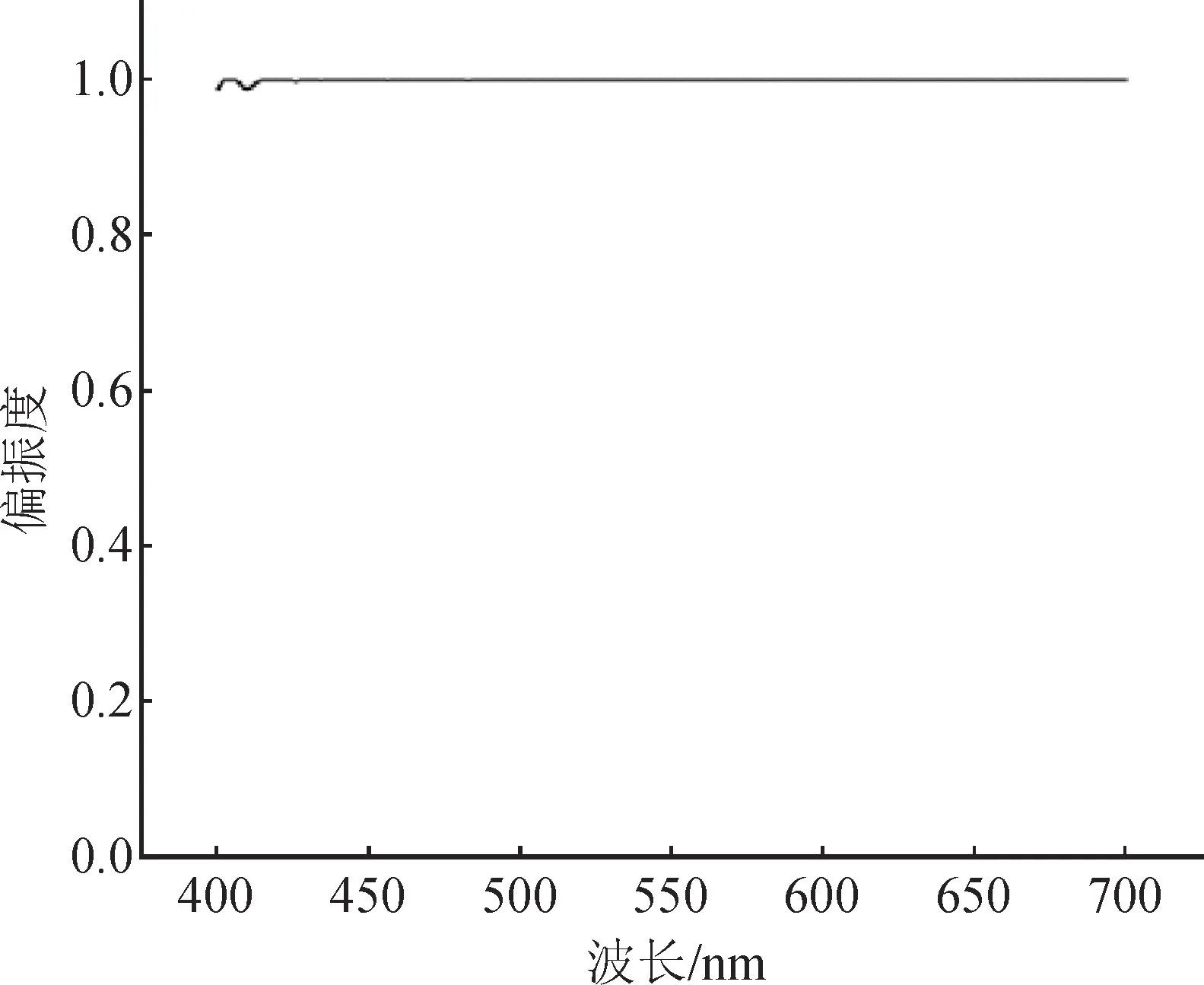
图3 入射光的偏振度曲线Fig.3 Polarization degree of the input light
光源的约化Stokes分量的色散曲线如图4所示,在本文研究的波段范围内(450~650 nm)入射光十分接近右旋偏振光(Stokes矢量为(1 0 0 1)T)。
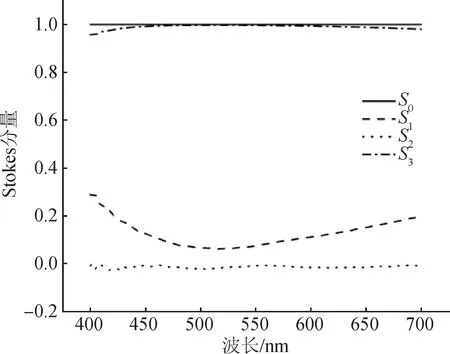
图4 入射光的Stokes分量Fig.4 Stokes vector of the input light
经待测偏光片作用后,入射偏振光的偏振度以及约化Stokes分量分别如图5和图6所示。由于高分子材料在短波波段可能存在的散射吸收作用,出射光在短波段的偏振度有所下降,但是在显示器行业比较关注的波段450~650 nm中,偏振度相对较高。出射光的约化Stokes矢量表明出射光是椭圆偏振光,S3≠0,表明偏光片基材具有轻微的二向色性,这主要是因为偏光片制造过程中需要对基材进行拉伸造成的。

图5 出射光的偏振度曲线Fig.5 Polarization degree of the output light

图6 出射光的Stokes分量Fig.6 Stokes vector of the output light
椭圆偏振光的主轴方向可由公式(9)计算得到,将其代入公式(6),通过最优化算法,结合输入输出光的Stokes分量,计算得出偏光片的透过率。将本方法的测量结果与Cary5000分光光度计的测量结果进行对比,如图7所示。

图7 测量结果与Cary5000分光光度计测量结果的对比Fig.7 Comparison of the measurement result and the result measured by Cary5000 spectrophotometer

图7表明基于Stokes矢量分析方法的测量结果误差在2%以内。产生误差的主要原因是光路中偏振棱镜与光轴不完全垂直造成的偏振光成分不单一,经过进一步的光路调整,测量误差可以得到有效降低[6-9]。
透过率的测量不确定度分析依据JJF 1059.1-2012《测量不确定度评定和表示》进行[10],具体计算过程如下:
1)光轴偏离中心引起的不确定度分量u1
偏振棱镜的接收角有限,具有一定发散角的光源发出的光进入偏振棱镜后,出射光中同时具有寻常光和非寻常光,由此引起的透过率的测量误差为3%,按照均匀分布计算其不确定度分量为
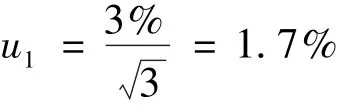
2)偏光片不均匀性引起的不确定度分量u2
偏光片测量得到的透过率最大值和最小值之差为0.9%,按照均匀分布计算其不确定度分量为
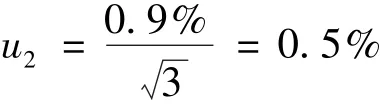
3)测量重复性引起的不确定度分量u3
透过率测量重复性引起的不确定度分量按照A类不确定度评定方法进行评定,计算结果为

4)光谱仪测量误差引起的不确定度分量u4
光谱仪测量误差引起的不确定度分量取其溯源标准不确定度

各不确定度分量之间相互独立,按照标准不确定度的合成原理,透过率的合成不确定度1.8%,取包含因子k=2,扩展不确定度为U=3.6%(k=2)。
3 结论
平板显示产业对多种偏振光学薄膜材料(例如偏光膜、相位补偿膜等)有着巨大的需求,相关材料的偏振光学性能测试对保障显示器质量具有重要意义。本文提出的基于Stokes矢量分析测量偏光片光学参数的方法相较传统测量方法具有更快的速度,更加适用于偏光膜生产线中的质量监控;而且该方法具有很好的普适性及可扩展性,只需要更改最优化算法即可适用于其他种类的偏振光学薄膜测量,例如相位差膜等[11-12],为推动平板显示产业高质量发展提供了有力支撑。

