声学测温研究现状及发展总结

赵乂鋆,赵俭

(航空工业北京长城计量测试技术研究所,北京100095）

0 引言

温度测量在日常生活、机械加工、材料合成、生物医学等领域有着广泛的应用[1]。随着科学技术的进步和实际应用的需要,温度测量向着响应更快、精度更高、鲁棒性更好的方向发展。在高温、高流速、强干扰等各具特点的温场环境下,非侵入式测温、穿透式测温、广域测温等温度测量要求逐渐被提出,越来越多的测温方式因此进入到人们的视野中,并在不同领域发挥着各自的优势。

测温方法可以分为接触式测温和非接触式测温两大类,其中发展最早的是接触式测温,即将传感器的敏感元件直接与待测物体接触进行温度测量,例如热电偶测温和热电阻测温等。然而,传统的接触式测温方法在强电磁干扰和强辐射影响的环境中测温能力有限,并不能完全满足复杂环境中温度计量的需求。近些年,接触式测温领域发展出了利用超声波和声表面波进行测温的方法,可解决部分复杂条件下温度测量的问题,扩大了接触式测温的应用范围。其基本原理及目前发展情况将在后文中进行介绍。

随着科学技术的发展,对于熔铸炉膛、等离子体室、核反应堆等[2]复杂环境温度测量的要求越来越高。上述环境具有以下共同点:待测物体处于高温或超高温环境中、待测物体处于封闭空间内部或因具有较强腐蚀性而不能直接进行接触式测温、测温环境受到强电磁或强辐射干扰。在这些情况下,接触式测温方法很难再有效发挥作用,需要采用非接触式测温方法。非接触式测温方法,是指敏感元件不直接与待测物体接触,通过测量待测物体的温度相关参数从而对温度进行还原的测温方法。非接触式测温方法主要可分为光学法和非接触式声学法,其中光学法可分为光谱法和辐射法[3]。光谱法和辐射法都具有时空分辨力高、响应速度快、测温上限高等优势。但光谱法对于机械装配和光源配置的要求很高,若测温环境中多振动、沙尘,或温度低于某个值时,其测量精度会大受影响。辐射法虽然对装配精度要求相对较低,但是复杂环境中待测物体表面发射率的变化会对其测量精度造成较大影响。非接触式声学测温是近50年来逐渐发展起来的方法,其基本原理是:声波在待测物质中传播时,温度作用使得声速或幅值发生改变,通过测得对应参数的改变情况反解得出声波通过路径的温度。非接触式声学测温具有温场还原准确性较高、结构简单、抗烟尘、抗震动、测温范围广的特点[1],是温度测量领域的重点研究方向之一。

本文对声学测温的基本原理以及发展现状进行介绍,并对未来声学测温的具体研究方向及亟待解决的问题进行分析。在此基础上,总结接触式声学测温方法及非接触式声学测温方法的优势以及不足之处,为促进声学测温技术进一步发展和完善起到归纳和指导作用。

1 声学测温分类

最早的声学测温理论始于气流温度测量,早在1687年,牛顿就推导出声速和气流温度存在特定的关系,随后在拉普拉斯的修改和订正下,新的声速与气流温度的关系式于1817年正式面世。数十年后,Mayer提出通过声速测量气流介质温度的概念,并做了大量早期实验[4],验证了气流温度的平方根与声速确实存在单一函数关系。1885年,英国物理学家瑞利发现一种沿物体表面传播的弹性波,即声表面波(SAW)。瑞利详细研究了声表面波的物理特性,并利用波动数学理论对其进行了证明[5]。至此,声学测温的基础理论已全部被发现,但受限于客观条件,这些实验当时并未引起人们的重视,直到20世纪70年代,人们才逐步认识到声学测温这一方法。20世纪90年代末期,超声检测固体内部损伤和缺陷的方法趋于成熟,学者们在研究中发现固体和液体内部声速和声衰减值和温度有单值函数关系,并逐渐发展为利用超声波测量物体内部温度或还原温度场的方法。

经过多年发展,现已有多种声学测温方法得到广泛应用。按照敏感元件是否直接与待测物接触,对目前典型的声学测温方法进行分类,如表1所示。

表1 声学测温分类与其特点Tab.1 Catagory and characteristics of acoustic thermometry

2 接触式声学测温

接触式声学测温方法可分为超声波内部接触式测温方法和声表面波接触式测温方法两大类。接触式声学测温方法要求声发射和声接收探头与待测物体接触,必要时还需要在接触处涂抹耦合剂并令接触处的压力恒定,使声波尽量不受接触边界的干扰。

2.1 超声波内部接触式测温

超声波接内部触式测温的基本原理是热声耦合,根据热弹性动力学理论,固体介质中的波速和声衰减主要由物体的弹性率和密度决定。通过测得波速和声幅值衰减的变化,可以反演出物体内部的温度场及其变化。在固体和液体中,声波存在横波和纵波两种传播形式。由于横波的质点振动方向沿声波传播的垂直方向,因此横波只能在固体、液体中传播;由于超声波具有良好的指向性,且对结构内部产生的影响可忽略不计,故可选择超声波对固体进行测温。

在不考虑边界影响的情况下,声速由密度ρ、弹性模量E和泊松比υ决定,即

式中:c纵与c横分别为纵波和横波在固体中的传播速度;G为剪切弹性模量。

一般来说,在固体材料中,弹性模量随着温度的升高而减小,故在大部分材料中,超声波速度随着温度的升高而降低。例如,在钢结构中,若温度低于500℃,纵波的声速变化率约为0.8 m/(s·℃),横波的声速变化率约为0.4 m/(s·℃)[6]。在测得声速之后,即可根据热传导等式以及超声波的传播路径反演二维甚至三维的温度场重建算法。以二维为例,根据傅里叶定律可以推导出,二维无内热源热传导控制方程为

式中:ρ为密度;T为温度;q为热流密度;cp为热容;k为导热系数;x,y为声波传播的平面坐标系中的坐标。

令声波在介质中传播的时间为声波的飞渡时间,则声波的路径方程为

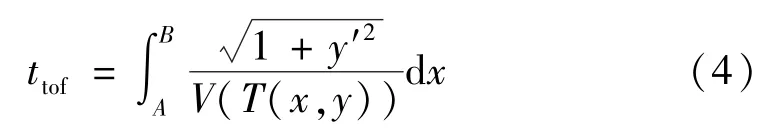
式中:ttof为声波的飞渡时间;A、B分别为声波的发射点和接收点。

求解声波路径,等价于求解泛函ttof(y)关于函数y(x)取极值的问题,再将热传导的控制方程代入其中,便可以反演出二维温度场。同理,利用该方法也可以还原三维温度场的温度分布,从而实现对体积较大的航空部件及加工过程中被测物体的整体温度场的还原。当超声波作用于液体时,仍满足相关方程。若以水为传播介质,则超声波波速可表示为

式中:S为超声波传播的路径距离;T为温度;P为水下压力;c0,0,0为常数,其值为1402.392;ΔcT,ΔcS和ΔcP分别为温度,距离和压力的拟合函数式;ΔcSTP为与温度,距离和压力都相关的拟合函数式,详见参考文献[7]。

通过对液体介质中超声波波速的测量,可以实现对诸如深海海域整体温度的测量及监测。声速测试装置简图如图1所示。

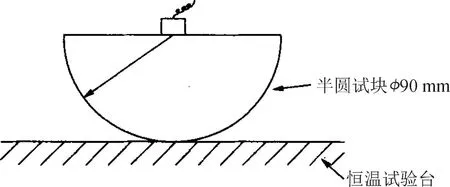
图1 声速测试装置简图Fig.1 Diagram of sound-velocity test device

除了声速之外,声衰减的幅值也与温度有一定的关系。Darbari认为:在高温下,超声波衰减变化的主要因素取决于纵波声速VL的-4次方,即

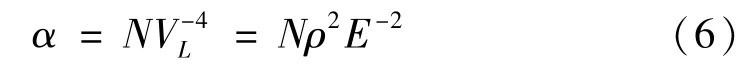
式中:α为衰减系数;N为包含其他因数和常数的“归一化因数”;ρ为密度;E为弹性模量;VL为纵波声速。

式(6)中,由于其他因数和常数包含内容不易确定,导致N的获取较为困难。实际上,即使在不考虑温度时,超声波的衰减系数也受到频率、波长、晶粒度、各项异性等因素的影响[6],使得衰减系数的确定较为困难,研究进展缓慢。故在研究超声波接触式测温时,研究人员大多采用以声速与温度耦合为原理的超声波接触式测温,而以声衰减与温度耦合为原理的研究则较少。在固体温度的测量方面,超声波内部接触式测温适用于尺寸较小或形状不规整的固体温度测量,也可应用于封闭空间的内部温度监测中;在液体温度的测量方面,由于实际液体环境较固体更为复杂,测温精度易受到影响,因此超声波内部接触式测温更多地应用于江河或海域的整体水温监测中。

目前,超声波内部接触式测温在测量固体内部温度场方面的研究还处于实验室研究水平,暂未形成成熟的工业产品。国内的研究人员利用射线声学预测声波路径的传播以及进行瞬态边界反演[7],误差已小于3%,但在探测点的数量和分布方面还需要开展更多研究;也有国内研究人员利用类似原理进行三维温度场还原研究[8],该课题组将奇异值分解的方法推广到三维空间中进行建模计算并开展了试验验证,得到的结果为:在对称单点热源的情况下,测温误差(方差)为1.46%,在多点热源的情况下,测温误差为2.09%。三维温度场还原示意图如图2所示。

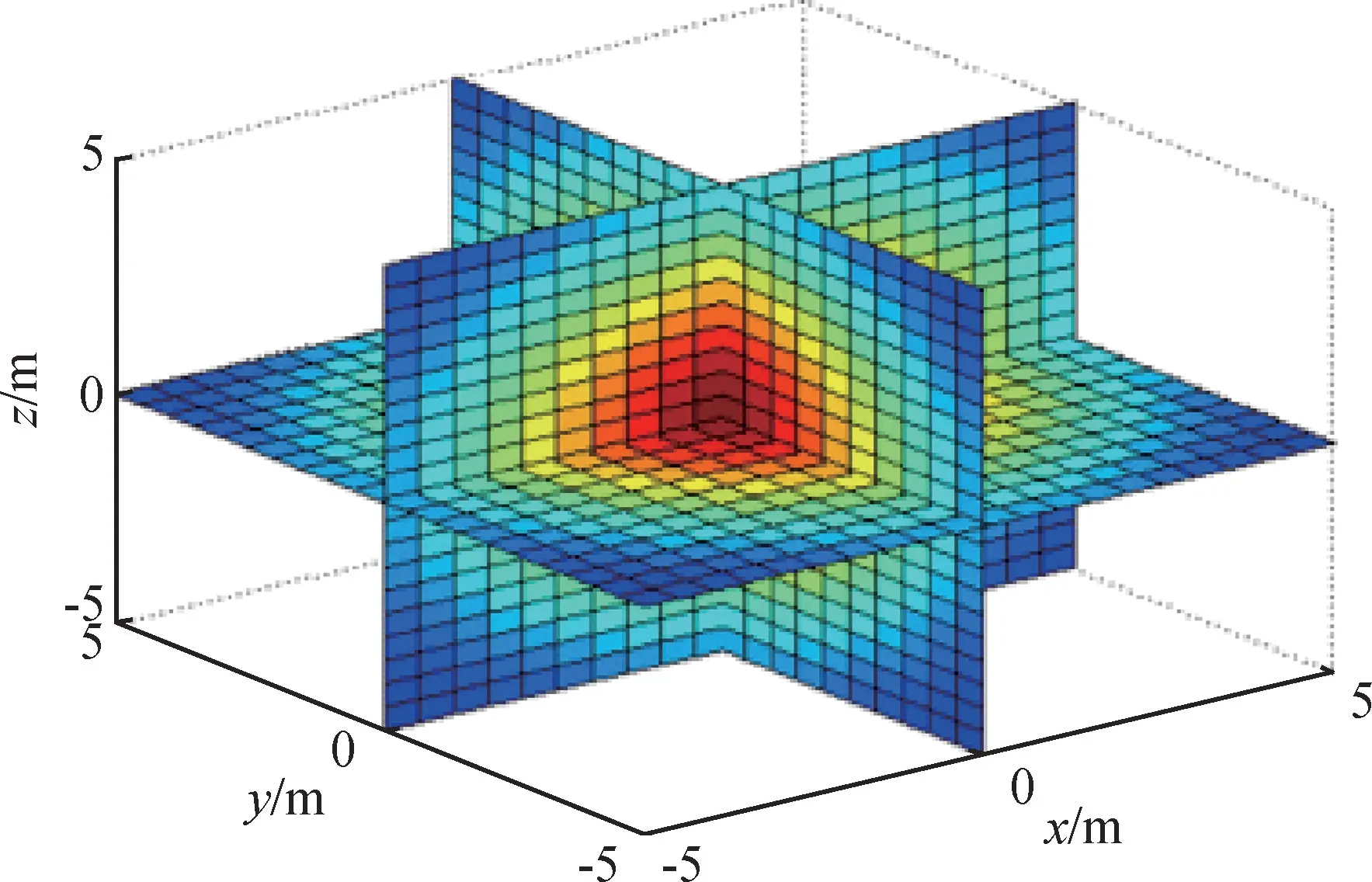
图2 三维温度场还原示意图Fig.2 Diagram of three-dimensional temperature field distribution reconstruction

国外学者利用特制的铁制探头作为接触式测温的探点,以测量多个回波之间的平均时间差作为声波路径时间的方式为基础架构,搭建了一套用于消融监测的超声波内部接触式测温系统,其监测示意图如图3所示。

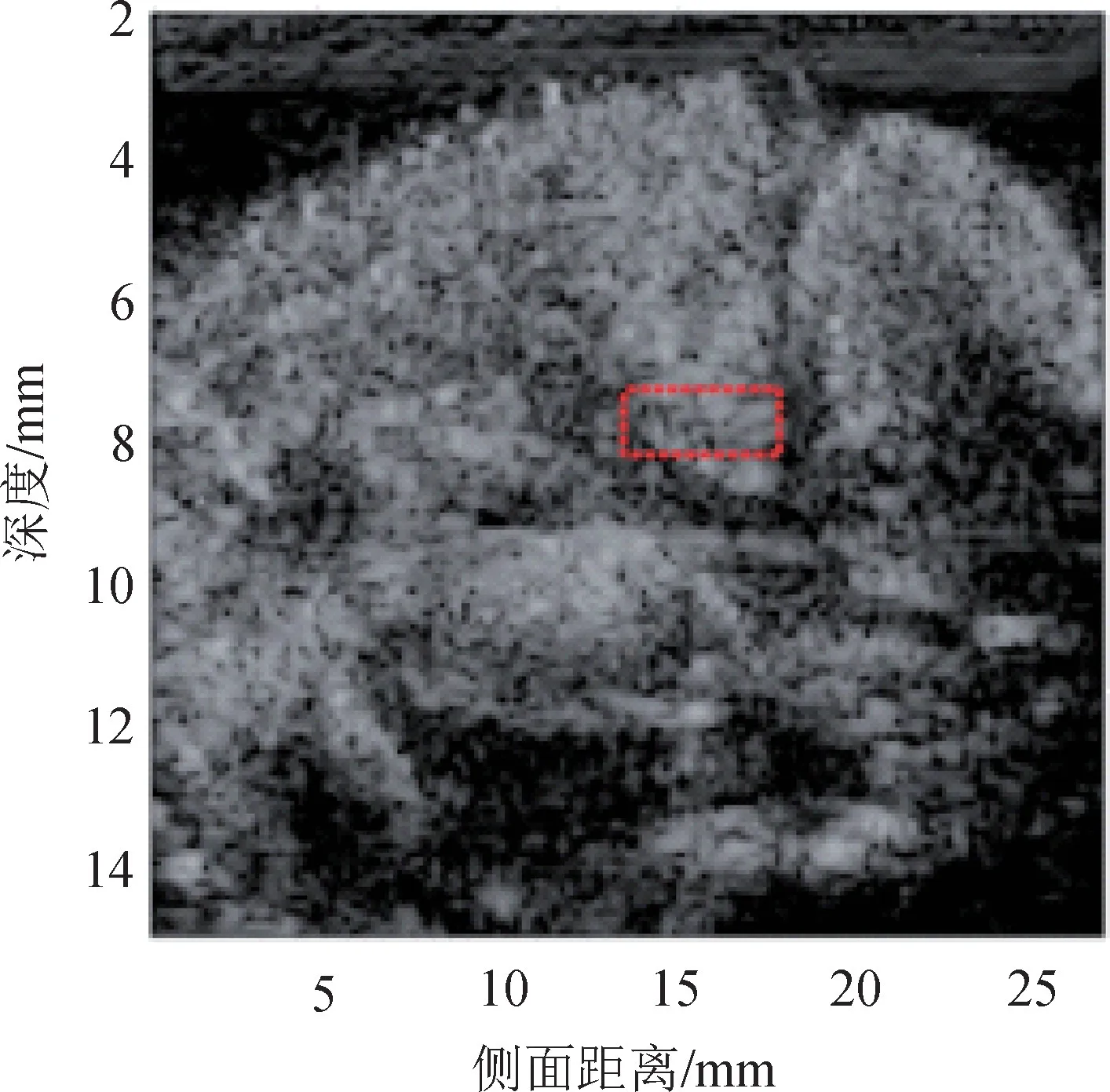
图3 消融监测示意图Fig.3 Diagram of ablation monitoring

该系统将声学测温与被动控制相结合,实现了50℃以下的高精度线性测量,具有较好的鲁棒性,测量误差在±0.015℃以内[9]。

超声波内部接触式测温应用于液体温度测量时,一般并不还原温度场,而是测量整条声波路径上的平均温度,用于实现水域平均温度的监测。目前应用于江水流域的平均温度测量误差为1.7%,可测量数十米距离范围的平均水域温度[10]。

2.2 声表面波接触式测温

从定义上来说,声表面波(SAW)属于超声波中的一种,在分类时将声表面波接触式测温与超声波内部接触式测温区分开的主要依据是温度的测量范围。超声波内部接触式测温反映的是物体内部的温场,声波的路径与入射的角度也有关系。而声表面波是一种能量集中在物体表面传播的弹性波,其声速、频率等会随着被测物体的温度、压力等变化而变化。声表面波传感器是通过测量声速、频率反演出温度、压力等相关参数的无源无线传感器,主要工作于50 MHz～2.5 GHz[5],由感受温度变化的SAW器件和激励、接收SAW信号的读写器构成。其中SAW器件由压电晶体、叉指换能器、天线以及相应的电路网络构成。使用SAW温度传感器时,将敏感器件放置于物体表面,通过读写器接收控制信号并将其转换为SAW信号进行温度感知,最终将带有温度信息的SAW信号转换为电磁信号传回。按照芯片器件的功能,SAW温度传感器可分为谐振型和延迟线两种结构。谐振型结构和延迟线结构的SAW温度传感器均是在叉指换能器的基础上实现的。故在介绍两种结构之前,首先介绍叉指换能器,叉指换能器示意图如图4所示。

图4 叉指换能器示意图Fig.4 Diagram of interdigital transducer

叉指换能器由许多金属膜电极组成,这些电极都附在压电材料的衬底上,且相互交叉放置,两端通过汇流条连接。叉指周期T=2a+2b,一对相互交叉的电极构成一个电极对,其相互重叠的长度为有效指长,即换能器的孔径w。叉指换能器的中心频率f0和带宽fbw如式(7)和式(8)所示[11]。

式中:ν0和λ0分别为SAW的穿透波速和波长,与温度等参数相关;NP为电极对的数目。

谐振型声表面波谐振器如图5(a)所示,压电晶体换能器左右各有一个声学谐振腔,中间的叉指换能器进行电-声-电的互相转换。当温度变化时,SAW传播速度变化,进而引起谐振腔的频率改变。波形在谐振腔内来回传播并叠加,当外部信号激励与中心频率相等时,谐振腔产生谐振驻波。通过测量谐振腔的频率,即可实现对温度的测量。

延迟线声表面波谐振器如图5(b)所示,叉指换能器在接收到激励信号后发射SAW,SAW传播一定距离后经反射栅条依次返回,最后转换为电信号从天线射出。延迟线结构的SAW温度传感器通过检测接收信号的时间或相位实现温度的测量。

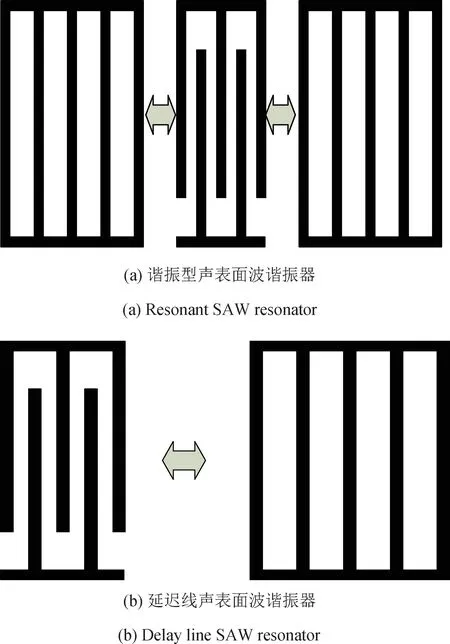
图5 谐振型和延迟线声表面波谐振器Fig.5 Resonant and delay line SAW resonator

谐振型和延迟线SAW温度传感器都具有无源无线、多点测量、灵敏度高、可靠性好、小巧轻便、易于生产[12]的特点,在多参数测量领域具有优势。谐振型SAW温度传感器相较延迟线SAW温度传感器具有温度灵敏性高、可靠性好、无线传输距离远的优点,因此应用更为广泛;延迟线SAW温度传感器则在灵活方便地测量多物理量数据方面具有不可忽略的优势。

目前,国外声表面波传感器经过发展,已形成了成熟的基础理论和技术配置,并已投入到了实际的生产生活中,在智能电网、高压传输线测温、高温炉膛测温等领域已有成熟的应用产品,例如美国的EVHT-100传感器,其工作范围为150～900℃,分辨力优于5℃,寿命大于500 h,支持无线传输及多传感器阵列组网[5],而目前国内暂无高温SAW传感器的应用实例。

目前低温SAW传感器的技术成熟程度不及高温SAW传感器,但也有部分应用产品。武汉烽火孵化电气公司应用于电网开关柜的SAW温度传感器,其测温距离为2.5 m,测温范围为-20～125℃,准确度为±1℃。国外的SENTRY SENSOR公司采用SAW延迟线结构,制作了一款应用于柴油发动机、发电机和压缩机的温度传感器,其测温范围为0～200℃,最大传输距离为50 mm。也有一些公司制作了功耗较低的SAW低温传感器[5],其最远通讯距离为3 m,主要应用于智能电网的组网中。

3 非接触式声学测温

非接触式声学测温具有测温范围广、精度高、速度快、可靠性较好的特点[2]。由于非接触式声学测温的介质主要是气流,而声波在气流中以纵波的形式进行传播,故在研究非接触式声学测温时只需研究纵波的传播特性即可。按照测温原理,非接触式声学测温可分为声速法和声共鸣法,其中声速法测温主要应用于气流温度测量,声共鸣法测温主要用于计量热力学中的玻尔兹曼常数。

3.1 声速法非接触式测温

声速法非接触式测温的原理是根据一维微元运动公式[13]推导得出的,即

式中:c为温场中的声速;γ为被测介质的绝热状态指数;R,M分别为摩尔气体常数和气体摩尔质量;T为热力学温度;Z为常数,若被测介质是空气,一般值取为20.05。

从式(9)中可以看出,声速c和温度T在理想情况下是单值对应关系,即当声波路径确定时,测得声波的飞渡时间即可计算得出这段路径的平均声速,之后可计算得到该路径上的平均温度。若有多条声波路径已知,即可利用Radon变换[14]实现二维平面的温度场还原式中:f为欧式空间中的点函数;x为二维平面上的点坐标;dl为路径L的线微分;θ为微分方向与路径方向的夹角;P为图像的投影。

由式(9)和式(10)的分析可知,当被测介质的浓度和成分稳定时,可通过测量声波飞渡时间来还原温度场。一般来说,当设置好声发射和声接收探头后,声波飞渡时间可由互相关法计算得到。目前还发展出希尔伯特变换法以及相关峰插值法以提高声波飞渡时间的测量精度。希尔伯特变换法即通过希尔伯特变换求得获取到的声波信号包络[15],即

式中:(t)为连续时间信号x(t)的希尔伯特变换;t为时间;*为卷积运算符号;j为复数符号;y(t)为x(t)的信号包络。

获取包络之后,便可以通过计算机软件准确地获取相关函数的最大值分离点,降低温场还原的误差。相关峰插值法是对互相关函数进行抛物线插值的方法[16],如图6所示。

图6 相关峰抛物线插值示意图Fig.6 Diagram of correlation peak parabola interpolation

设互相关函数在B点取得最大值,对应横坐标为n,令信号的采样频率为f,则可将n/f作为对应的时延估计代入抛物线方程中。当dy/dx=0时,抛物线取得最大值,将此时的横坐标值作为修正之后的飞渡时间值,可以提高时延估计的精度。

1986年,日本的伊藤文夫和坂井正康提出以最小二乘法作为最初的温场还原算法。最小二乘法的原理是:将整个待测平面划分为若干相同的像素,再根据声速与温度的关系计算出每一个像素的平均温度,最后采用插值的方式还原整个温度场。最小二乘法因其简单快速的矩阵运算一直沿用至今。研究人员在温场还原算法领域还提出了傅里叶正则算法、高斯函数展开法、基于BP神经网络的还原方法以及基于径向基函数的奇异值分解方法等,这些方法都是通过不同的算法将温场还原的公式展开,舍去发散项和高阶小量后,再合并化简后的展开式获取温场的。以基于径向基函数的奇异值分解方法(SVD)为例[17]进行说明,如图7所示。

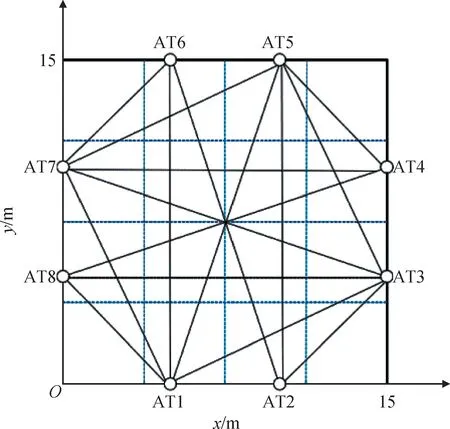
图7 经典平面温度场划分Fig.7 Classical division of temperature field

径向基函数计算公式为

式中:γi(x,y)为温度场中第i个区域的的径向基函数;(x,y)为待考察点的坐标;(xi,yi)为第i个区域的几何中心坐标;H为该径向基的形状参数。

将温场划分矩阵D通过径向基函数求取广义逆D+,再利用飞渡时间矩阵与其相乘便可以重建温场。基于径向基函数的奇异值分解方法虽然相较最小二乘法计算耗时更长,但其精度和收敛性较好,是用于温场还原的重要算法。

在经过了数十年时间的研究后,国外研究人员逐一阐明了声速法测温的基础原理,温场的重建算法,飞渡时间的数字处理,声速法测温的成像机理以及弯曲效应的弥补原理,使得声速法测温的基础原理基本完善,测量范围与精确度充分提高,理论技术已逐步成熟。美国SEI公司的Boilerwatch声速法温度测量系统可测温度范围为0～1927℃,分辨力为6.7℃,刷新时间为5 s。而国内在实验室环境中研究追赶多年,在以工业炉膛环境为基础模型的温度场测量研究中,颜华等人[17]提出以截断奇异值分解(TSVD)的方式处理测量数据,得到的实验结果如图8所示。

图8 截断奇异值分解重建温场Fig.8 TSVD method of temperature field reconstruction

截断奇异值分解方式相较于一般奇异值分解方式具有更好的鲁棒性以及更弱的病态性,能够提高温场还原算法的准确度。根据图8中的试验结果可知,其测量误差不高于0.31%;在1600 K高温风洞的恶劣环境中,超声测温传感器的准确度可达97%[2],与国外成熟的研究成果之间的差距日渐缩小。

国内还有学者提出将非接触式声速法测温应用于粮仓温度监控以及航空发动机燃烧室气流温度测量中。其中,应用于粮仓温度监测时,可将声波传播路径等效为直径很小的声波导管,在此基础上进行相关研究,最后通过实验得到在1.2 m边长的模拟储存大豆的粮仓中,不同热点数的温度场重建误差均在1%以内,能够进行即时有效的温度监测[18]。在航空发动机燃烧室气流温度测量中,针对低温和低流速时的分析和实验较多,而在高温、高流速的环境下实验时,受声波路径弯曲效应和气流声速矢量合成的影响,温度场的重建误差在10%以上[13],仍需要通过进一步的研究和实验进行修正和改进。

3.2 声共鸣法非接触式测温

自2018年国际计量大会正式通过新的基本单位定义之后,热力学温度的计量从传统的依赖于实物转变为测量平衡态系统的状态参数。对于温度而言,这个参数就是玻尔兹曼常数kB。在实践中,人们发现之前的国际温标T90与以kB为定义的温标T存在误差,且该误差随着温度的增大而增大,故需要采用新的方法对T90进行修正。其中气体声学温度计具有最广的温度适用范围和最小的不确定度[19],其测量热力学温度的随机偏差已达到5×10-6水平。气体声学温度计的基本原理主要可分为两种,即(准)圆球共鸣法和圆柱共鸣法。(准)圆球共鸣法具有较高的能量品质因数与较小的边界层效应,国际上多采用此方法,但是其加工要求非常高;圆柱共鸣法的结构比较稳定,加工制作的难度也相对较低。由于圆柱共鸣法是相对独立的方法,可避免由于单一方法产生的系统误差,在直接测量热力学温度方面更具前景,但该方法的能量品质因数较低,需要开展更多的研究。气体声学温度计的基本原理为

式中:c为声速;下标s表示在等熵条件下;γ0为单原子气体比热比;NA为阿伏伽德罗常数;M为气体摩尔质量。

由式(14)分析可知,要得到玻尔兹曼常数,需要准确地测得声速。在获得了声速之后,便可确定待测的热力学温度

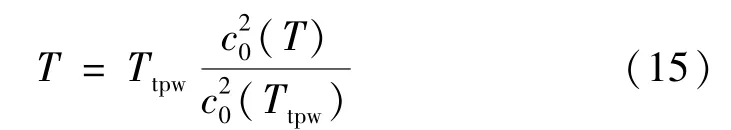
式中:T为待测热力学温度;Ttpw为水的三相点温度;c0为理想气体状态下的声速。

气体声学温度计应用声共鸣方法,通过测量声学共振频率及微波谐振频率计算获得气相声速后,采用声学温度计相对法计算获得热力学温度。测量声速的主要方法包括定程法与变程法。变程法的原理是在共鸣腔内部安装2块平行板,在平板上分别安装声信号的发射和接收装置,测量时,声接收装置接收移动的声发射装置发出的声信号,根据变程引起的变化进行反演运算。定程法则是根据已知尺寸的腔体内干涉波信号确定气相声速。由于定程法消除了变程法中的平板位移误差,因此具有更高的精度,是目前较为常用的方法。

声发射和声接收装置一般采用电容式麦克风,近些年也有采用压电陶瓷式和端盖薄膜的方法。以定程式圆柱共鸣腔为例,如图9所示。

图9 圆柱共鸣腔Fig.9 Cylindrical resonant cavity

圆柱共鸣腔长为L,其声波轴非缔合理想共鸣频率为

式中:c为声速;l为声波的轴向特征数;f0为理想共振频率。

考虑到非理想因素的扰动,实测共鸣频率f N可以表示为理想共振频率f0的线性叠加[20],因此共鸣频率表示为复数形式

式中:FN为测量模式的复数共振频率;N为非理想因素的个数;g N为实测共鸣频率的半宽;Δfj和Δgj为第j个非理想因素对实测共鸣频率及其半宽的扰动效应。

由分析可知,当圆柱形声波导管的半径a增大而轴向特征数l减小时,有利于声波信号的传输,但此时非理想的扰动也会增大。在确定好圆柱的形状之后,实验[20]发现以压电陶瓷作为声发射装置,以电容式麦克风作为声接收装置时,其接收信号的信噪比、灵敏度均优于其他组合方式,能够进一步降低测量热力学温度时的不确定度。

目前,利用声学测量玻尔兹曼常数的温度存在限制,大多数的测量均在300 K以内,而对于600 K以上的温度区域还是空白。国外学者以(准)圆球共鸣法为基础,研究并测量了323 K以内的玻尔兹曼常数,并将误差控制在2×10-5左右[21]。国内研制的圆柱形声波导管在导管内径越大、长度越短的情况下更利于声波的传输。据此,国内学者在该理论的基础上研究了600～1358 K区间的声学共鸣理论,并在300 K的条件下对该理论的普适性进行了测试实验,得到的误差为3×10-5[19],为国际温标T90误差的修正提供了可靠的数据支持。

4 总结及展望

声学测温是一种具有良好前景的无损测温方式,为各种复杂环境下的温度测量提供了重要解决方案。声学测温不会对原温场产生较大影响,相互作用带来的测温误差较小,温场还原的准确性也较高。此外,声学测温探头的抗震性能和抗烟尘性能也较好,且易于布置,测温范围也较广[1]。目前,除了应用于气流温度测量之外,非接触式声学测温还可应用于仓库的失火检测中。接触式声学测温则在高压电力设备温度监控、核反应堆内部温度还原、水域平均温度的测量、监控加工过程中的消融反应及超导失导等方面有着广泛应用。在日常生活方面,接触式声学测温也可应用于人体内部温度测量以及水果生鲜运输途中的温度监测等。声学测温在诸多领域已得到广泛应用[22-27],对实现高效准确的温度测量具有重要意义。

目前,声学测温技术也存在一些需要解决的问题:

①根据费马原理,在测量非均匀温度场时,声波路径会向温度高的一侧弯曲,因此声波实际传播的路径长度和理论计算的路径长度之间必然存在误差,该误差会对声波飞渡时间的计算以及温度场的还原造成影响。

②被测温场内部若存在多种成分,或是不同成分的占比动态变化等情况,均会影响温场还原的计算公式。此时,一些常参数将成为变量,测得的声波飞渡时间等会和理论值有差距,进而导致温场重建存在较大误差。

③声学测温中,声学温度传感器的敏感元件直接暴露在外进行开放式测温,不进行单独的屏蔽和封装[12],开放式的测量方法使得声学温度传感器的安装较为简单,但也使得声波探头更容易受到现场环境噪声的影响,导致测量准确性降低。

针对问题①的解决方法除了通过仿真拟合进行修正之外,还可以采用以斯涅尔定律为原理的三角向前法则,即通过初步得到的温度场及流速场计算声波在微元路径上的移动距离和出射矢量方向,再将计算后得到的路径结果反馈回算法中,对温度场进行修正,以此提高温度场的还原精度。针对问题②,实验中通常采用先理论计算,后仿真拟合的方式使得这方面的原理误差降低,提高温度场的还原精度。针对问题③,可通过实验选择合适的声探头中心频率,降低声探头接收噪声信号的能力;或采用合适的滤波方法滤除环境中的噪声,减少噪声对声信号的干扰。

以上均为目前常见的提升声学测温准确性的方法。在未来的工作中,需要继续在这些方法的基础上开展更加深入的研究,包括声学测温的基础公式在各种不同测温环境下的修正、声波飞渡时间获取中滤波和互相关算法的精度及稳定度提升、温度场还原算法计算速率的提升及奇异性消除、声波路径弯曲效应的理论计算与拟合等。在解决上述问题之后,声学温度传感器在温度计量方面的应用将更加广泛。