一类三角函数的定积分求解技巧
2021-02-10 02:49:02郑宝杰段宇轩
河南教育学院学报(自然科学版) 2021年4期
郑宝杰, 段宇轩
(河南财政金融学院 统计与数学学院,河南 郑州 450046)
0 引言
常用的定积分计算方法有牛顿-莱布尼茨公式,换元积分法和分部积分法。对于一些复杂的定积分,其计算方法通常具有很强的灵活性和技巧性[1-4]。本文主要对一类被积函数是三角函数的定积分的计算做了进一步的推广和应用。
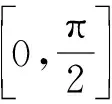
引例1计算
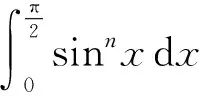
解当n=2m时,
当n=2m+1时,

因而这两个定积分是等值的。
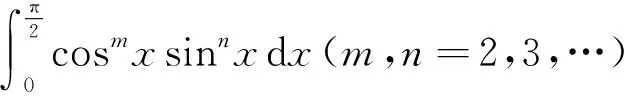
重复使用递推公式可得
(1)
当m或n为0时,即为引例1的结果。
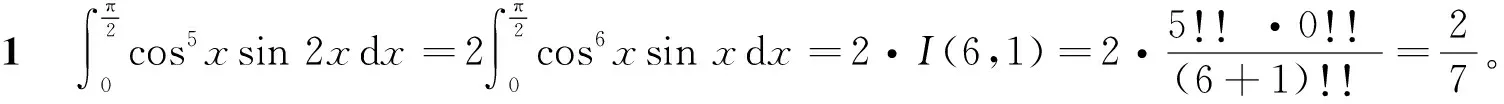
1 推广和应用
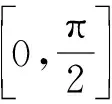
1)当m或n至少有一个为奇数时。
解法1令F(x)=cosmx·sinnx(x∈[0,2π])。
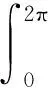
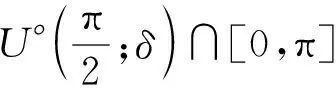
解法2
①当m、n均为奇数或m为偶数,n为奇数时,
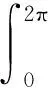
②当m为奇数,n为偶数时,
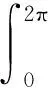
2)当m、n均为偶数时。
由周期性可知
综合上面的讨论结果可得定积分计算公式如定理1所示。
定理1设m和n为正整数,则有
(2)
特别地,从上面的讨论过程中发现,由于sinx和cosx均为周期为2π的周期函数,则当积分区间上下限之差为2π时,计算公式也为式(2)。
推论设m和n为正整数,对任意α∈R,有
(3)
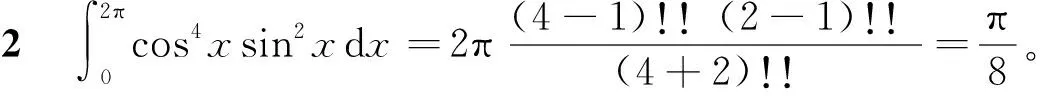
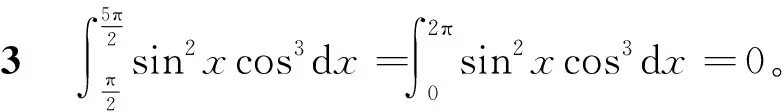
2 另一公式的推广和应用
文献[5]有这样一个证明题:
引例2设f为连续函数,证明
(4)
下面通过sinx与cosx之间的变换对公式(4)进行推广,可得定理2。
定理2设f为连续函数,证明
(5)
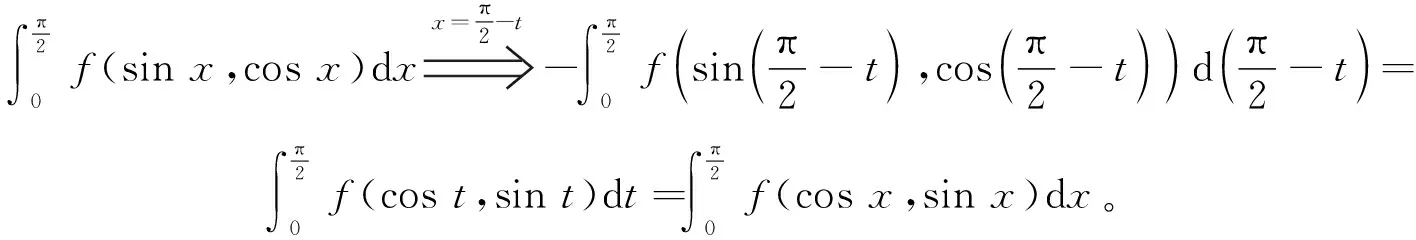
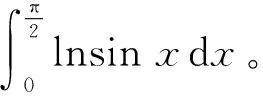
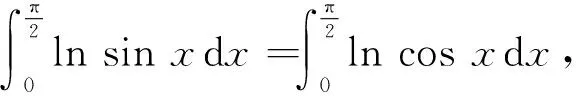
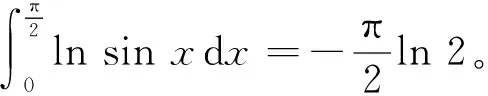
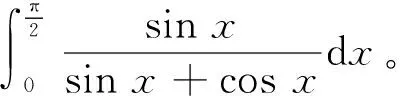
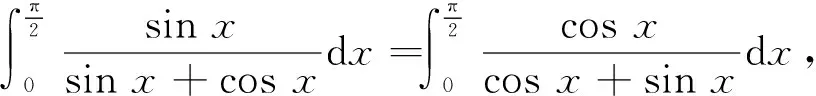
因此
有时sinx或者cosx难以计算,这样计算的好处是通过互换后相加或者其他运算得到更简单的运算,计算出结果。
3 小结
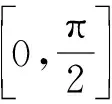
猜你喜欢
小猕猴智力画刊(2021年11期)2021-11-28 21:30:15
小学生学习指导(低年级)(2021年5期)2021-07-21 02:01:04
南京大学学报(数学半年刊)(2020年1期)2020-03-19 02:24:44
求知导刊(2017年30期)2018-01-17 10:22:05
课程教育研究·新教师教学(2015年12期)2017-09-27 16:09:40
广东教育·高中(2017年7期)2017-09-01 20:22:19
高中生·天天向上(2016年5期)2016-11-21 05:44:58
福建中学数学(2016年2期)2016-10-19 11:54:48
振动工程学报(2015年2期)2015-03-01 01:16:04
燕山大学学报(2014年4期)2014-03-11 15:28:50

