发生教学法在行列式概念教学中的运用

张俊忠， 邓喜才， 陈松良

(贵州师范学院 数学与大数据学院，贵州 贵阳 550018)

教育部《关于深化本科教育教学改革 全面提高人才培养质量的意见(教高2019)》指出：“强化人才培养方案、教学过程和教学考核等方面的质量要求，引导学生多读书、深思考、善提问、勤实践。”[1]因此要积极尝试大学教育新模式，提高教育质量。大学数学教育的基本目标是要让学生掌握扎实的数学知识，拥有较强的数学能力，具备丰富的数学思想，形成积极的创新精神。要实现目标，必须坚持大学数学教学研究、实施教学改革。发生教学法关注数学知识的起源、发生发展过程，有利于学生形成科学的数学观，促进学生可持续发展。

1 发生教学法的提出

1866年德国动物学家、进化论者海克尔在论著《生物体普通形态学》中指出：“个体发育是种群成长的迅速而浓缩的重演。”即生物发生律[2]。将生物发生律迁移到人类的认识论，则个体的认知发生是人类认识产生、发展过程的重演。对于数学教育，即个体对数学知识的学习过程必须遵循数学知识的客观发生过程。因此要求教师通过数学的发展过程了解人类是如何获得数学认识的，从而对学生应该如何领悟这些认识进行更好地再创造。把数学的产生过程作为教学线索，不具体谈论数学史，通过数学的发展过程启示指导教学，这就是发生教学法[3]。

2 发生教学法的策略

发生教学法的运用目的是通过探索知识的起源，激发学生学习动机，追寻首创者的历史背景，弄清解决问题的关键因素。从心理的角度看，不了解问题的来龙去脉是很难解决问题的。数学发生教学法的根基是数学史，但是数学史仅仅是促进教育，方便掌握数学知识的素材，不是单纯的历史。发生教学法借鉴历史引入主题，保护学生猎奇的天性，通过引导学生重现知识的再发现过程，培养学生的创新精神。实施发生教学法关键在教师，要求教师深刻认识教学主题的来龙去脉、发展过程，透彻掌握教学主题发生过程中的关键因素、重要环节，完全理解从一个阶段发展到下一个阶段的原因是什么，会遇到哪些障碍和困难。为了促进教学，设计教学主题发展过程的某些关键环节，设计符合认知规律、环环相扣的问题。

3 发生教学法在行列式概念教学中的实践

3.1 全面了解行列式的历史

作为高等代数的一个分支，行列式理论有着悠久的历史。在东方，中国的《九章算术》大约成书于公元1世纪，其中“方程”一章，专门研究解线性方程组。当时没有表示未知数的符号，而是用算筹将未知数的系数和常数项排列成一个长方阵，运用遍乘直除算法求解，这就是消元法。宋元时期出现了天元术和四元术，这是中国古代数学代数符号化的一个进步，元朝朱世杰(1249—1314)的《四元玉鉴》，已经可以解含4个未知数的高次方程组。中国的天元术和方程术著作中，《算学启蒙》和《杨辉算法》在日本经过广泛传播，影响很大。日本关孝和(1642—1708)在《解伏题之法》中，构造行列式展开法以解决多元高次方程组的消元问题。关孝和的解伏题是中国天元术、四元术代数传统的继续，核心是消元理论。关孝和提出行列式算法后，日本一批数学家开始研究行列式，如井关知辰在《算法发挥》中第一次提出行列式可以按照某一行或某一列展开。久留岛义太关注3阶到6阶行列式的展开，特别是对5阶、6阶行列式，提出采用分块构造低阶小行列式，再按照行展开。菅野元健也研究了行列式的展开，实际上是拉普拉斯展开法，但是给出的子行列式相乘的符号法则不正确，后来由加藤平左卫门指出此错误。

在西方，德国莱布尼兹(1646—1716)是第一位研究行列式的数学家。他的行列式思想主要体现在与法国洛必达(1661—1705)的通信和他自己未发表的手稿中，他首创了双标码记法。虽然他没有命名行列式，而且没有及时发表他的思想，但是他仍然被尊称为西方行列式理论的鼻祖。法国马克劳林(1698—1746)用比莱布尼兹更具体的形式，利用行列式解线性方程组，马克劳林为行列式理论的初期建立迈出了一大步。瑞士克莱姆(1704—1752)是独立发现行列式基础思想的数学家，他的克莱姆法则在理论上是一个非常漂亮的结果。将行列式作为独立对象研究是从法国范得蒙(1735—1796)开始的，他的法国同胞拉普拉斯(1749—1827)和拉格朗日(1736—1813)也为行列式理论作出了杰出贡献。范得蒙是第一个对行列式本身进行研究的数学家，因此被认为是行列式理论的奠基者。他提出了用2阶子式和对应的余子式展开行列式的方法，但是没有给出证明。范得蒙认为行列式展开式中正、负项各占一半。拉普拉斯广泛研究行列式，证明和推广了范得蒙的一些结论，得到拉普拉斯展开法，为发展和完善行列式理论奠定了坚实的基础。德国高斯(1777—1855)从数论的角度研究行列式，虽然没有给出行列式概念，但是渗透在计算方法中。法国柯西(1789—1857)从函数角度研究行列式，使行列式理论的发展进入新局面。英国凯莱(1821—1895)给出了行列式展开规则，更重要的是引入行列式符号。用一对竖线置于方阵两侧，成了直到今日还在使用的行列式符号。德国魏尔斯特拉斯(1815—1897)用公理化方法定义行列式，把行列式作为一个具有线性、齐次特征的函数[4]。

3.2 掌握行列式的各种定义是关键

根据数学概念的定义原则，从不同角度定义行列式，可以归纳为4种。

1)抽象定义法。n阶行列式

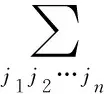
2)归纳定义法。

①当n=1时，规定|a11|=a11；

②假设(n-1)阶行列式已经定义，则n阶行列式A=a1j1A1j1+a2j2A2j2+…+anjnAnjn，其中aij是行列式A的元素，Aij是A中元素aij的代数余子式，i,j=1,2,…,n[6]。

3)公理定义法。

称Mn(F)到F的映射f:A→f(A)为矩阵A的行列式映射，记为f(A)=|A|，如果满足以下3个条件：

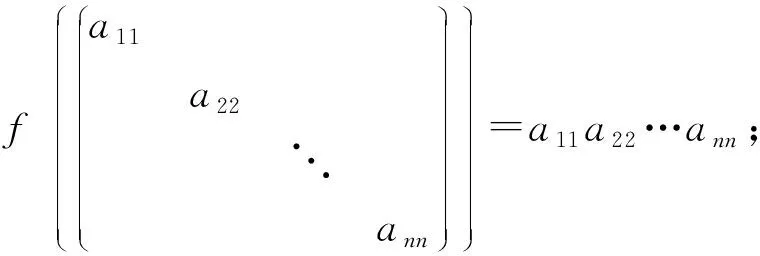
② 对任意的i,1≤i≤n,和任意的c∈F,有f((α1…cαi…αn))=cf((α1…αi…αn))；

③ 对任意的i,j(1≤i

Mn(F)表示数域F上全体n阶方阵的集合，n阶方阵A=(aij)nn∈Mn(F),用α1,α2,…,αn分别表示A的各个列向量，此时(α1α2…αn)=A[7]。

4)几何定义法。

行列式的几何定义是：1阶行列式是有向线段的代数长，2阶行列式是有向面积的代数和，3阶行列式或以上是有向体积的代数和。这个代数和要注意每个面积或体积的方向，方向相同的要加，方向相反的要减[8]。

上述4种定义都是等价的，只是侧重点不同。第1种定义容易让学生深层次认识行列式的本质，体现了数学的严密逻辑性和高度抽象性，有利于发展学生的逻辑推理能力;第2种定义具体，学生预备知识不需要太多，适合循序渐进原则，有利于学生快速掌握概念;第3种定义注重形式，结构简单，学生很容易掌握行列式性质，有利于培养学生公理化思想;第4种定义形象直观，学生容易理解和记忆行列式的性质，有利于培养学生直观想象的数学素养。下面以数学专业学生学习行列式第一种定义为例，研究如何设计教学过程。

3.3 学习行列式定义的困惑与障碍

大学数学专业的学生，已经具备数学核心素养，可以独立地发现和提出问题、分析和解决问题，拥有较高的思维能力和创新能力。这样的学生学习行列式的定义，总会有许多疑问:为什么有行列式概念？为什么要这样定义行列式？行列式性质很多，如何有效记住和掌握这些性质？学习行列式的价值是什么？于是在行列式概念的教学中，一定要启发学生、引导学生解决这些问题。只有明白了这些，学生才能彻底了解行列式知识的来龙去脉，深刻认识行列式在自己数学知识结构中的位置，这样才能有利于新知识和新思想方法的建构[9]。

3.4 根据历史，重构课堂

3.4.1 创设情境，引入新知

利用对角线法则，

提出问题：如果四元一次方程组

有唯一解，请猜测其解的结果。

世界数学史上，行列式思想的萌芽有两个分支，一支来自东方，一支来自西方。日本数学家关孝和在《解伏题之法》中，为了解决多元高次方程组的消元问题，第一次创造了行列式展开法。德国数学家莱布尼兹是西方第一位研究行列式的数学家，是西方行列式理论的鼻祖，他为了解决线性方程组的消元问题，提出了行列式思想。实际上，不管是东方还是西方，都是因为解方程组的消元问题，为了书写和使用的方便，促进了行列式思想的产生。

3.4.2 自主探索，展示过程

有同学通过类比认为

的展开式是

a11a22a33a44+a14a21a32a43+a13a24a31a42+a12a23a34a41-a14a23a32a41-a11a24a33a42-a12a21a34a43-a13a22a31a44。

实际上通过消元法解此方程组，如果有唯一解，D的值是24项的代数和，而不是8项的代数和，不能再用对角线法则求4阶行列式的值，即用对角线法则不能求所有行列式的值。这也说明类比推理、归纳推理是合情推理，得到的结论不一定是真命题。合情推理的结论虽然不一定正确，但是合情推理有利于发展创造力。

通过2阶、3阶、4阶行列式的结果，请学生总结n阶行列式项的一般特征。2阶是2项、3阶是6项、4阶是24项，可以猜测n阶行列式有n！项。2阶、3阶、4阶行列式中带正号项和带负号项各占一半，可以猜测n阶行列式中带正号项和带负号项各占一半，即都有n!/2项。2阶中每项2个元素分别来自不同的2行和2列，3阶中每项3个元素分别来自不同的3行和3列，4阶中每项4个元素分别来自不同的4行和4列，则可猜测n阶行列式中每项n个元素分别来自不同的n行和n列。2阶中当行下标是自然排列时，带正号项的列下标是偶排列，带负号项的列下标是奇排列。3阶中当行下标是自然排列时，带正号项的列下标是偶排列，带负号项的列下标是奇排列。4阶中当行下标是自然排列时，带正号项的列下标是偶排列，带负号项的列下标是奇排列。可以猜测n阶行列式当行下标是自然排列时，列下标是偶排列的项带正号，列下标是奇排列的项带负号。因此猜测n阶行列式展开后的总体特征应该是：n阶行列式展开后是n！项的代数和，每项是n个元素的积，这n个元素来自不同的n行和n列。当行下标是自然排列时，列下标是偶排列的项带正号，列下标是奇排列的项带负号。

关孝和是东方第一位给出行列式思想的数学家，他提出的交式、斜乘行列式展开法存在缺陷，只能解决3阶及以下阶行列式的展开，而4阶及以上阶行列式不能用对角线法则展开。其后日本的数学家们发现了此缺陷，积极予以纠正。由于连续不断修改，关孝和展开法趋于完善。莱布尼兹通过双标码记法，第一次引入行列式概念。

3.4.3 数学抽象，建构概念

根据前面分析，n阶行列式其实也可以先固定n列，将每项元素的列下标确定为自然排列，则

根据排列的性质，若i1i2…in，j1j2…jn都是1，2，…，n这n个数码的一个排列，则

(-1)π(i1i2…in)+π(j1j2…jn)ai1j1ai2j2…ainjn=(-1)π(p1p2…pn)a1p1a2p2…anpn，

其中p1p2…pn是元素交换位置后产生的新列下标排列。既然如此，n阶行列式也可以先固定任意一个行下标排列，只要列下标取所有组合的排列，即n!项。或者先固定任意一个列下标排列，只要行下标取所有组合的排列，即n!项。

关孝和之后，日本有一批数学家开始研究行列式，如井关知辰提出行列式可以按照某一行或某一列展开。久留岛义太提出5阶、6阶行列式，可以采用构造低阶小行列式，再按照行展开。不研究解方程组，将行列式作为专门研究对象是从范得蒙开始的，他是第一位对行列式本身进行研究的数学家，是行列式理论的奠基者。范得蒙给出了用2阶子式和它们的余子式来展开行列式的方法。拉普拉斯证明和推广了范得蒙的一些结论，给出拉普拉斯展开法，促进了行列式理论的进一步发展。

3.4.4 深挖内涵，总结性质

例1已经定义了行列式，根据定义计算行列式

的值。

分析行列式A展开虽然有5！项，即120项，但是除了项a11a22a33a44a55，其余项中的元素至少有一个为0，即该项为0，故A=a11a22a33a44a55。同理B=a11a22a33a44a55。

显然根据行列式定义求一个行列式的值很繁琐，但是如果行列式像上面A或B，结果很简单，直接是其中几个元素的积。像上面A或B形式的行列式分别叫下三角行列式或上三角行列式，a11，a22，a33，a44，a55称作是主对角线上的元素。如果一个行列式能够转化为用下三角行列式或上三角行列式表示，那么行列式的值很容易计算。现在研究行列式性质，辅助化简和计算行列式。

由行列式定义和排列反序数知识，可得

1)转置性质：行列式与它的转置行列式相等。

2)变号性质：交换行列式的两行(或两列)，行列式变号。

3)提公因子性质：行列式某行(或某列)所有元素的公因子可以提到行列式符号外。

4)行列式为0性质：

①行列式有2行(或2列)完全相同，则其值为0；

②行列式某行(或列)的元素全是0，则其值为0；

③行列式有2行(或2列)的对应元素成比例，则其值为0。

5)和的性质：行列式对某行(或列)具有可加性。

6)变形同值性质：行列式某一行(或列)的元素乘以同一数加到另一行(或列)的对应元素上，其值不变[10]。

行列式性质很多，如果根据名称和内容记忆性质，那么就能够灵活利用性质计算行列式。

例2计算n阶行列式D的值,

分析此行列式根据定义计算很困难，看是否能够通过变形将它转化为用上三角行列式或下三角行列式表示。经过观察可以发现，该行列式在每行或每列中的元素，除了一个元素是0，其余n-1个元素都是1。于是可以考虑将第2行、第3行……第n行的元素都加到的第1行对应元素上，此时第1行的n个元素都是n-1。这时将第1行的公因子n-1提到行列式符号的外边，可以根据变形同值性质，将行列式转化为用上三角行列式或下三角行列式表示。

任何行列式只通过行变形同值性质可以变为上三角行列式或下三角行列式，任何行列式只通过列变形同值性质可以变为上三角行列式或下三角行列式，通过行或列变形同值性质可以变为对角行列式(既是上三角行列式，又是下三角行列式的行列式)。

高斯从数论的角度研究行列式，首创“行列式”这个词。柯西从函数的角度研究行列式，给出行列式定义。凯莱提出了行列式展开规则，引入了行列式符号。用一对竖线置于一方阵两侧，成了普遍使用的行列式符号。魏尔斯特拉斯用公理化方法研究行列式。

3.4.5 综合应用，巩固新知

前面利用行列式的定义和性质进行了行列式的化简和计算，现在利用行列式知识进行有关行列式的推理论证。

例3设在n阶行列式

中，aij=-aji,i,j=1,2,…,n。

证明当n是奇数时，D=0。

分析此题如果根据行列式定义进行推理论证，有些困难，估计要用行列式的性质解决。首先要了解此行列式元素的特征，根据特征确定方法。

解因为aij=-aij，所以，当i=j时，aii=-aii，故aii=0， 则

当n是奇数时，D=-D。故D=0。

行列式概念内涵丰富，性质较多，要通过适当的练习巩固和加深印象，这样才能掌握其本质，才能为后续知识的学习作好铺垫。行列式不仅在解线性方程组和多元高次方程组中有应用，而且在矩阵理论、向量空间和其他学科中都有广泛的应用，因此必须学懂弄通行列式。实际上关于行列式的定义，目前各种著作中采用的一般有4种方法，分别是抽象定义法、归纳定义法、公理定义法、几何定义法。本文介绍的是抽象定义法，另外3种方法需要学生自己阅读和学习[11]。

本设计中行列式概念是基于学生已有的具体认识，通过学生自己探索行列式的一般特征，师生共同建构形成的，不仅发展了学生的合情推理能力和抽象概括能力，而且也让学生体会了数学知识的创造过程，为学生将来研究数学积累了经验。行列式概念建立后，结合排列知识，通过研究行列式的性质，发展学生的演绎推理能力。由于性质多，避免用数目简单罗列性质的形式，将性质分类并采用特定名称，这样学生理解和运用性质很方便，提高了学习效率。通过文献学习，不仅能够领悟行列式内涵的丰富性，而且能够认识数学体系建构方式的多样性。因此，应用发生教学法不仅有利于促进学生学习新知识、掌握新思想，而且能够培养学生探索精神，养成科学态度。